Яновский Б.М. Земной Магнетизм. Том 2

Подождите немного. Документ загружается.

ГЛАВА V

МАГНИТНОЕ ПОЛЕ ТЕЛ ПРАВИЛЬНОЙ

ГЕОМЕТРИЧЕСКОЙ ФОРМЫ

§ 1. Прямая и обратная задачи геофизики

Задача нахождения источников магнитной аномалии, т. е.

тех пород, которые вызывают данную аномалию по наблюдае-

мому распределению магнитного поля на Поверхности Земли,

носит название обратной геофизической задачи.

В теории потенциала доказывается, что если нет никаких

данных об источниках магнитного поля, кроме распределения

поля на поверхности, обратная задача однозначно не решается.

Такое заключение вытекает из теоремы Стокса, которая

утверждает, что если известно распределение потенциала на

замкнутой поверхности, а масса M заключается внутри этой по-

верхности, то этим самым определяется потенциал во всем

внешнем пространстве, независимо от распределения массы

внутри поверхности. Отсюда вытекает, что если перераспреде-

лить массы внутри поверхности так, чтобы потенциал на поверх-

ности остался тем же самым, то потенциал во всем пространстве

вне поверхности остается неизменным. Этот результат показы-

вает, что, зная лишь потенциал вне источника, нельзя опреде-

лить положение и форму источника.

То же самое относится и к случаю, когда известно распреде-

ление первой производной потенциала на замкнутой поверхно-

сти,

т. е. известно распределение напряженности магнитного

поля.

Для однозначного решения обратной задачи, т.. е. для нахож-

дения размеров и формы тела, вызывающего потенциал, по тео-

реме, установленной П. С. Новиковым [49], необходимо знать

законы изменения плотности притягивающего тела. В частно-

сти,

из теории вытекает, что если плотность тела D постоянна,

то данный потенциал вызывается лишь одной определенной

формой, и, следовательно, по заданному потенциалу можно

определить форму тела, размеры же тела остаются при этом

неопределенными.

Этот вывод вытекает, однако, непосредственно из общих вы-

122

Магнитное поле тел

[Гл.

ражений для любого из потенциалов: объемного, поверхност-

ного и двойного слоя. Так, выражение объемного потенциала

при постоянной плотности тела D имеет вид:

где R — расстояние от какой-либо точки внутри тела, принимае-

мой за начало координат, до любой точки поверхности, на кото-

рой задан потенциал; ρ — расстояние от начала координат до

любой точки тела и θ — угол между R и р.

В этом случае обратная задача сводится к отысканию пре-

делов интеграла, т. е. параметров, определяющих поверхность

тела, по заданным значениям V и R.

Легко видеть, что эти параметры определяются с точностью

до постоянного множителя VD, Т. е. форма этой поверхности для

любого значения D будет одна и та же, размер же зависит от

величины плотности D.

Хотя принципиально форма поверхности тела при постоян-

ной его плотности по заданному распределению потенциала

и находится, однако решение уравнения (5.1) в общем виде не

представляется возможным. Поэтому нахождение ее произво-

дится путем сравнения наблюденного распределения потенциа-

ла или его первой производной с потенциалами тел, вычислен-

ными непосредственно по формуле

(5.1).

Задача нахождения потенциала по заданному объему и

форме тела носит название прямой задачи геофизики.

§ 2. Прямая задача магнитометрии для трехмерного пространства

Формы залегающих пород представляют собой бесконечное

разнообразие, не позволяющее выразить их какими-либо урав-

нениями; тем не менее каждую из них можно уподобить, в пер-

вом приближении, одной из геометрических правильных форм

(шар,

призма и пр.).

Основанием для этого служит тот факт, что на расстояниях,

значительно превышающих размеры самой породы, магнитное

поле эквивалентно полю однородно намагниченного шара. Дей-

ствительно, из разложения магнитного потенциала в ряд по

сферическим функциям следует, что при удалении точки Р, в

которой рассматривается потенциал, от источника поля члены

высших порядков по сравнению с первыми делаются малыми.

(5.1)

Прямая задача для трехмерного пространства

123

и ими можно пренебречь. Первый же член разложения пред-

ставляет потенциал однородно намагниченного шара.

Из всего многообразия трехмерных тел правильной геомет-

рической формы для магнитной разведки могут иметь значение:

шар,

круглый цилиндр, прямоугольная призма, эллипсоид вра-

щения, так как большинство пород, вызывающих аномалии и

находящихся на достаточной глубине, можно уподобить одной

из этих форм того или иного размера и расположенных самым

различным образом по отношению к земной поверхности.

Поэтому остановимся на вычислении потенциала и состав-

ляющих магнитного поля указанных тел, считая, что они намаг-

ничены однородно по той или иной геометрической оси. Решения

прямой задачи основаны на обычных законах магнитостатики и

главным образом на законе Кулона, при условии, что намагни-

ченность пород обусловлена наличием в них магнитных зарядов.

Предположение об однородности намагниченных горных по-

род вполне допустимо, так как магнитная восприимчивость их в

большинстве случаев порядка Ю

-2

—Ю

-3

и мало меняется в за-

висимости от намагниченности. Действительно, согласно выво-

дам намагниченность в любой точке породы определяется урав-

нением*

Λ+χΝ

Так как κ мало, а N для большинства пород меньше единицы,

то произведением χΝ можно пренебречь, и тогда

/=хЯ.

Если κ — величина постоянная, то / также будет постоянной для

всех.точек тела.

Шар. В соответствии с выводами § б гл. I тома I потенциал

однородно намагниченного шара в любой точке пространства,

имеющей сферические координаты: г, θ и λ, если начало коор-

динат поместить в центр шара, выражается уравнением:

—-[cos

θ cos

θο

+ sin θ sin θ

cos

(λ-λ

)],

(5.2)

при этом θο и λ

— координаты магнитного полюса и M — его

дмагнитный момент.

В практике полевых наблюдений распределение магнитного

поля дается на плоскости,-поэтому сферические координаты не-

обходимо заменить прямоугольными. Если принять за ось z-ов

линию, перпендикулярную к рассматриваемой плоскости

(рис.

55), и обозначить координаты точки Ρ через х, у, О, а коор-

динаты точки Q пересечения магнитной оси с плоскостью-через

л*о,

i/o, О и расстояние центра шара до начала координат

—

через

124 Магнитное поле тел [Гл. V

то

и, следовательно,

где х' = OQ и r

=O'Q, при этом, как легко можно видеть из

рис.

56,

Для практики достаточ-

но ограничиться рассмотре-

нием магнитного поля вдоль

линии OQ, представляющей

пересечение вертикальной

плоскости, проходящей че-

рез магнитную ось шара, с

горизонтальной плоскостью.

В этом случае угол λ—λο=0

и координата у=0, поэтому

Составляющие напря-

Рис. 55. К решению задачи о нахож- женности магнитного поля

дении поля над шаром.

п0

°си х и по оси ζ, т. е. го-

ризонтальная и вертикаль-

ная,

которые обозначим соответственно через Н

и Ζ

, очевидно,

выразятся как

(5.3)

Так как магнитный момент однородно намагниченного шара

представляет произведение объема шара υ на его намагничен-

ность /, то правые части уравнений (5.3) являются функциями

нулевого порядка и поэтому не зависят от масштаба, в котором

измеряются величины R, х, х

и радиус шара. Поэтому, приняв

за единицу длины расстояние R и выразив M через радиус

шара а и намагниченность /, получим:

Прямая задача для трехмерного пространства

125

(5.4)

В такой форме уравнения, когда а и χ выражены в еди-

ницах R при заданном значении угла наклона θο, не зависят ни

от глубины залегания шара, ни от его размеров, и графики, по-

строенные по этим формулам, будут справедливыми для любых

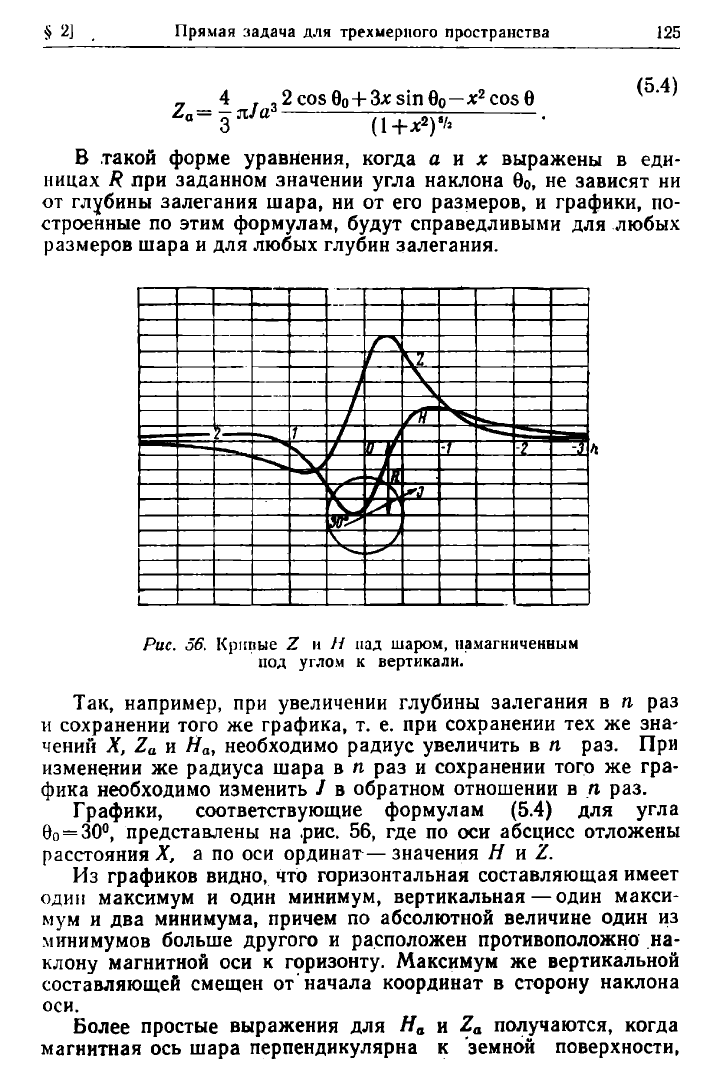
размеров шара и для любых глубин залегания.

Рис. 56. Кривые Ζ и // над шаром, намагниченным

под углом к вертикали.

Так, например, при увеличении глубины залегания в η раз

и сохранении того же графика, т. е. при сохранении тех же зна-

чений Χ, Ζα и #

, необходимо радиус увеличить в η раз. При

изменении же радиуса шара в η раз и сохранении того же гра-

фика необходимо изменить / в обратном отношении в η раз.

Графики, соответствующие формулам (5.4) для угла

θο

30°,

представлены на .рис. 56, где по оси абсцисс отложены

расстояния X, а по оси ординат — значения Η и Ζ.

Из графиков видно, что горизонтальная составляющая имеет

один максимум и один минимум, вертикальная — один макси-

мум и два минимума, причем по абсолютной величине один из

минимумов больше другого и расположен противоположно на-

клону магнитной оси к горизонту. Максимум же вертикальной

составляющей смещен от начала координат в сторону наклона

оси.

Более простые выражения для Н

и Ζ

получаются, когда

магнитная ось шара перпендикулярна к земной поверхности,

126

Магнитное поле тел [Гл. V

т. е. когда намагниченность шара направлена по вертикали.

В этом случае

Хо

= 0 и

= R и, следовательно,

(5.5)

Графики Н

и Z

в этом случае будут аналогичны графикам

(рис.

56), но симметричны относительно оси ординат, т. е.. мак-

симум Z

будет при χ = 0, а минимумы на одинаковых расстоя-

ниях χ от начала координат и по абсолютной величине равны

друг другу.

Легко видеть, что

Интересно также отметить, что для шара, намагниченность

которого параллельна горизонтальной плоскости, т. е. при

составляющие будут:

т. е. характер изменения их с расстоянием χ будет одинаков с

характером изменений соответственно Ζ

и Н

при вертикальной

намагниченности.

2. Прямолинейный стержень, намагниченный по направле-

нию геометрической оси. В природе такому геометрическому

образцу можно сопоставить штоки малого поперечного сечения

интрузивного происхождения.

Вследствие малости поперечных размеров таких штоков по

сравнению с глубиной залегания мы можем рассматривать маг-

нитные заряды, распределенные на торцовых поверхностях ци-

циндра, сосредоточенными в двух точках на концах штока.

Величина этих зарядов, очевидно, равна произведению намаг-

ниченности / на площадь основания цилиндра S, т. е.

m=/5.

Тело,

у которого магнитные заряды сосредоточены в двух

точках (полюсах), называется схематическим магнитом.

Прямая задача для трехмерного пространства

127

Магнитный потенциал схематического магнита определяется

из закона Кулона:

(5.6)

где /"t и г

— расстояния полюсов от точки Ρ (рис. 57).

Так же как и для шара, практически

достаточно рассмотреть распределение

поля вдоль линии, проходящей через

проекции полюсов +т и

—

m на гори-

зонтальную плоскость. Приняв ее за ось

лг-ов,

и обозначив координаты полюсов

+m и —m соответственно через Х\, R\ и

Х2,

R>, а координаты точки Ρ через χ и R.

получим:

(5.7)

Помещая начало координат в одном

из полюсов схематического магнита, т. е.

полагая Х\=0 и R\

0, а

=Хо

Ro,

будем иметь:

Рис. 57. К реше-

нию задачи о на-

хождении поля над

прямолинейным

стержнем.

(5.8)

при этом

Аналогично предыдущему случаю правые части этих урав-

нений— функции нулевого порядка, так как магнитный заряд

может быть представлен как произведение намагниченности на

площадь поперечного сечения центра.

Поэтому график, построенный в масштабе глубины залега-

ния верхнего полюса, при заданных значениях длины стержня

и угла наклона оси к горизонту будет одинаковым для любой

глубины залегания стержня и любых размеров площади попе-

речного сечения, если только размеры этой площади малы по

сравнению с глубиной залегания.

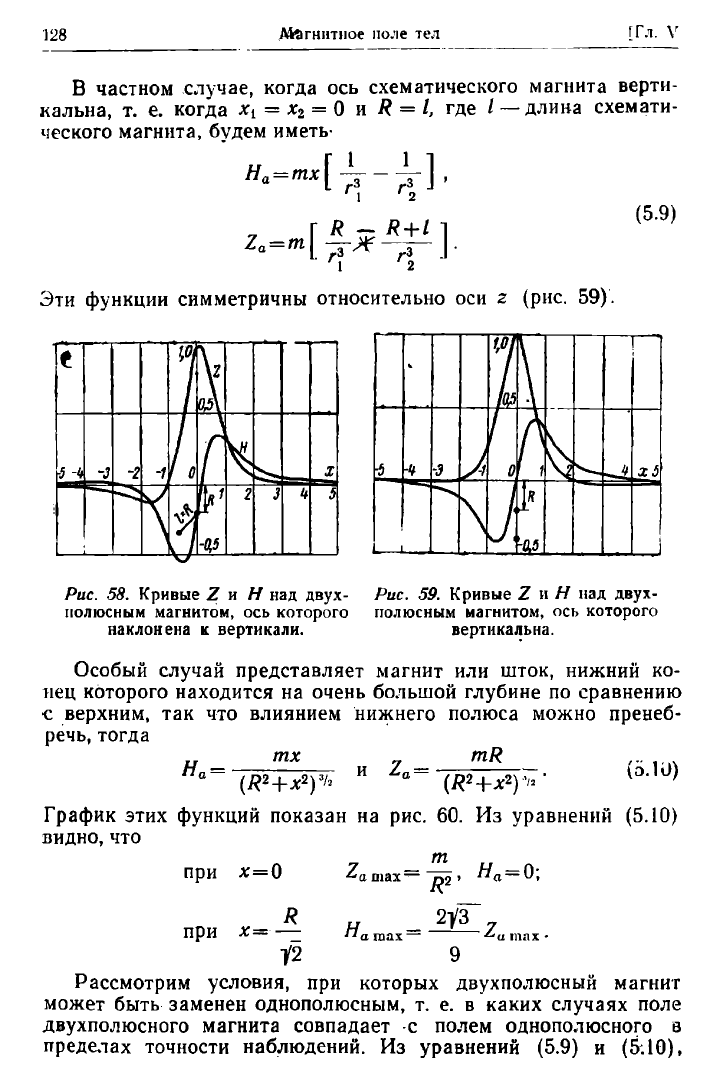
Подобные графики таких функций представлены на рис. 58.

По характеру они аналогичны графикам для шара с магнитной

осью,

наклоненной к горизонту.

Разница заключается в соотношении максимумов Н

и Z

максимума и минимума Ζ

и в расстоянии экстремальных зна-

чений Н

и Ζ

от начала координат.

128

Магнитное поле

тел

[Гл.

В частном случае, когда

ось

схематического магнита верти-

кальна,

т. е.

когда

Xi = х

= 0 и R = /, где / —

длина схемати-

ческого магнита, будем иметь-

(5.9)

Рис.

58.

Кривые

Ζ и Η над

двух-

полюсным магнитом,

ось

которого

наклонена

вертикали.

Особый случай представляет магнит

или

шток, нижний

ко-

нец которого находится

на

очень большой глубине

по

сравнению

с верхним,

так что

влиянием нижнего полюса можно пренеб-

речь,

тогда

Рассмотрим условия,

при

которых двухполюсный магнит

может быть заменен однополюсным,

т. е. в

каких случаях поле

двухполюсного магнита совпадает

полем однополюсного

пределах точности наблюдений.

Из

уравнений

(5.9) и (5.10),

Рис.

59.

Кривые

Ζ и Я над

двух-

полюсным магнитом,

ось

которого

вертикальна.

Эти функции симметричны относительно

оси ζ (рис. 59).

График этих функций показан

на рис. 60. Из

уравнений

(5.10)

видно,

что

Прямая задача для трехмерного пространства

129

(5.11)

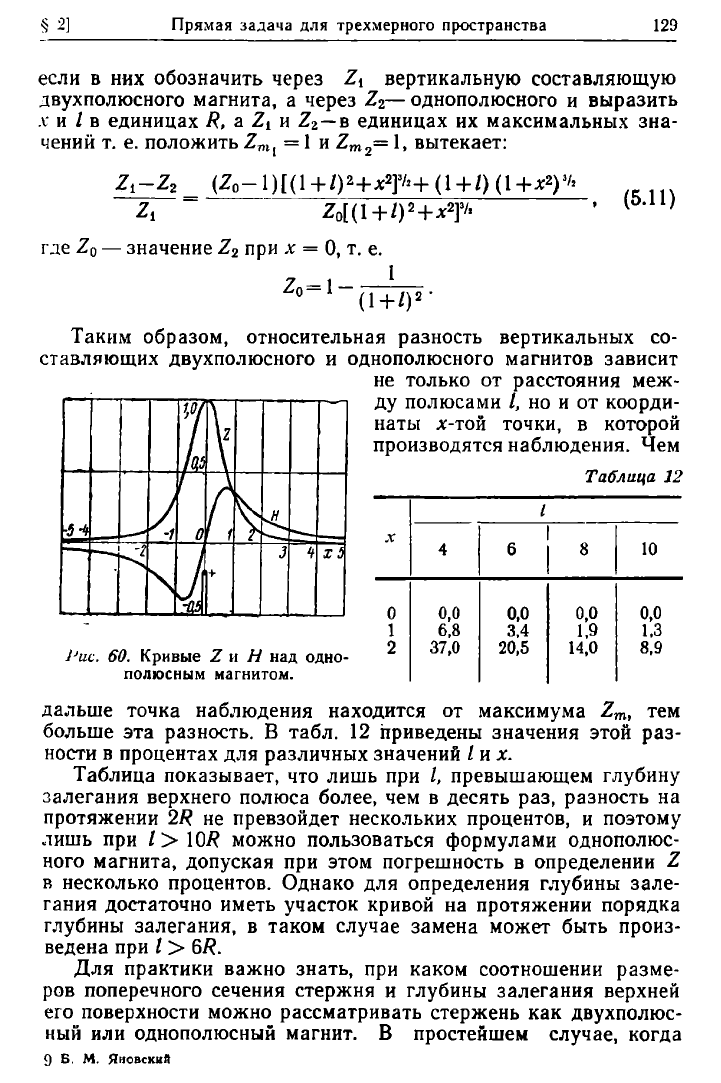
Таким образом, относительная разность вертикальных со-

ставляющих двухполюсного и однополюсного магнитов зависит

не только от расстояния меж-

ду полюсами I, но и от коорди-

наты *-той точки, в которой

производятся наблюдения. Чем

Таблица 12

X X

4 6 8 10

0,0

0,0 0,0

6,8

3,4

1,9

1.3

37,0

20,5

14,0 8,9

Рис. 60. Кривые Ζ и Η над одно-

полюсным магнитом.

дальше точка наблюдения находится от максимума Z

, тем

больше эта разность. В табл. 12 приведены значения этой раз-

ности в процентах для различных значений / и х.

Таблица показывает, что лишь при /, превышающем глубину

залегания верхнего полюса более, чем в десять раз, разность на

протяжении 2R не превзойдет нескольких процентов, и поэтому

лишь при 1>\0R можно пользоваться формулами однополюс-

ного магнита, допуская при этом погрешность в определении Ζ

в несколько процентов. Однако для определения глубины зале-

гания достаточно иметь участок кривой на протяжении порядка

глубины залегания, в таком случае замена может быть произ-

ведена при / > 6R.

Для практики важно знать, при каком соотношении разме-

ров поперечного сечения стержня и глубины залегания верхней

его поверхности можно рассматривать стержень как двухполюс-

ный или однополюсный магнит. В простейшем случае, когда

g Б. М. Яновский

если в них обозначить через Z

вертикальную составляющую

двухполюсного магнита, а через Z

— однополюсного и выразить

.с и / в единицах R, a Z

и Z

—в единицах их максимальных зна-

чений т. е. положить Z

и Z

= 1, вытекает:

где Z

— значение Z

при χ = 0, т. е.

130

Магнитное

поле тел

[Гл.

стержень представляет круглый цилиндр, нахождение магнит-

ного поля цилиндра с конечным радиусом основания представ-

ляет сложную математическую задачу, и поэтому решение ее

производится приближенными методами, изложенными в § 4

настоящей главы. Вычисления по этому методу показывают, что

относительная разность в процентах между вертикальной со-

ставляющей Z

цилиндра, у которого глубина залегания верх-

него основания в четыре раза больше радиуса цилиндра, и вер-

тикальной составляющей Zi точечного полюса в центре анома-

лии, не превосходит 7% и остается одинаковой на протяжении,

равном глубине залегания. Поэтому если верхнее основание

цилиндра залегает на глубине, превосходящей радиус цилиндра

не менее, чем в четыре раза, то такой цилиндр можно рассма-

тривать как точечный магнит. В этом случае вертикальная со-

ставляющая не имеет отрицательных значений.

§ 3. Прямая задача для двухмерного пространства

Большое число наблюдаемых аномалий представляет узкие

области, вытянутые в одном каком-либо направлении, примером

чего могут служить Курские аномалии. Такие аномалии обра-

зуются породами, простирающимися на большое расстояние

вдоль земной поверхности и имеющими поперечные размеры,

малые по сравнению с их длиной. Геометрическими образцами

их могут служить бесконечно длинные тела, расположенные па-

раллельно земной поверхности и имеющие в своем сечении круг,

эллипс, прямоугольник, параллелограмм.

В первом случае это будет бесконечно длинный круглый

цилиндр, во втором — эллиптический цилиндр и в третьем и

четвертом — бесконечно длинные призмы.

Магнитное поле любого из таких тел будет одинаково вдоль

линии, параллельной его оси, т. е. не зависит от одной из трех

координат.

Поэтому задача нахождения магнитного поля таких тел

носит название плоской или двухмерной задачи, так как реше-

ние ее сводится к нахождению потенциала плоской фигуры,

представляющей собой сечение бесконечного тела плоскостью,

перпендикулярной к оси этого тела.

Магнитный потенциал однородно намагниченной фигуры бу-

дем искать по теореме Пуассона

(5.12)

при этом вектор J должен лежать в плоскости сечения тела.

Гравитационный потенциал V плоской фигуры выражается

согласно теории потенциала формулой