Яновский Б.М. Земной Магнетизм. Том 2

Подождите немного. Документ загружается.

Прямая задача

для

двухмерного пространства

131

(5.13)

где

г —

расстояние элемента площади

dS до

рассматриваемой

точки, σ—поверхностная плотность,

данном случае равная

единице,

интегрирование распространяется

на всю

площадь

фигуры.

Подставляя

V в

формулу

(5.12),

получим выражение

для

магнитного потенциала плоской фигуры

(5.14)

Бесконечно длинный круглый цилиндр, намагниченный

перпендикулярно

оси и ось

которого параллельна земной

по-

верхности, эквивалентен однородно

намагниченной окружности. Поэтому

магнитный потенциал

его

найдем, если

проинтегрируем выражение

(5.14)

пределах площади окружности радиу-

са

а.

Такое интегрирование дает:

(5.15)

где

R —

расстояние

от

центра окруж-

ности

до

рассматриваемой точки

Ρ и

—

угол между

J и R (рис. 61).

Произведение

ло

есть магнитный

момент цилиндра длиной, равной еди-

нице,

радиусом

а.

Обозначая

его

через

μ,

будем иметь:

Как видно,

это

выражение

не

зависит

от

радиуса окружно-

сти,

определяется

ее

магнитным моментом

μ.

Поэтому

оно

справедливо

и для

окружности очень малого диаметра, которую

можно рассматривать

как

плоский диполь.

пространстве трех

измерений плоский диполь, очевидно, эквивалентен двухполюс-

ной бесконечно длинной нити,

и,

следовательно, выражение

(5.16)

является также

потенциалом такой нити.

Положим,

что

намагниченность цилиндра составляет

вер-

тикальной осью угол

, а

радиус-вектор

этой

же

осью —у гол

φ,

тогда

θ =

—

φο,

и,

следовательно,

(5.17)

Рис.

61. К

решению

за-

дачи

нахождении поля

над бесконечным цилинд-

ром.

(5.16)

132

Магнитное поле

тел

[Гл.

Переходя

от

полярных координат

прямоугольным,

по-

лучим:

откуда

(5.18)

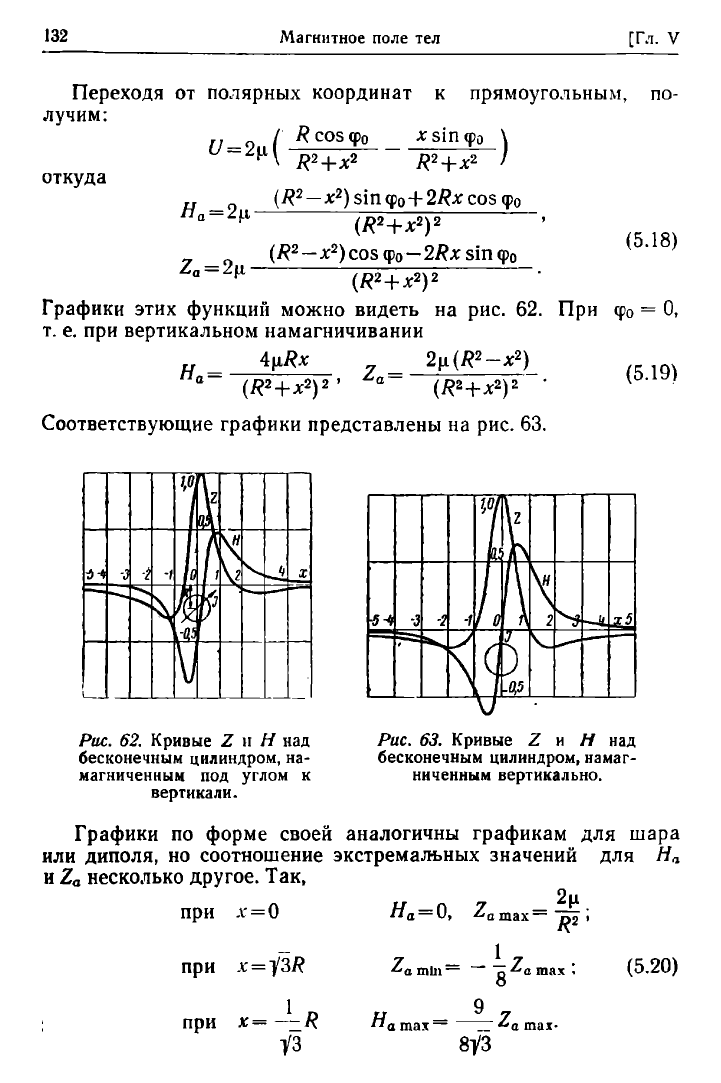
Графики этих функций можно видеть

на рис. 62. При φ

= О,

т.

е. при

вертикальном намагничивании

(5.19)

Соответствующие графики представлены

на рис. 63.

Рис.

62.

Кривые

Ζ и Η над

бесконечным цилиндром,

на-

магниченным

под

углом

вертикали.

Рис.

63.

Кривые

Ζ и Η над

бесконечным цилиндром, намаг-

ниченным вертикально.

Графики

по

форме своей аналогичны графикам

для

шара

или диполя,

но

соотношение экстремальных значений

для Н

несколько другое.

Так,

(5.20)

Прямая

задача

для

двухмерного пространства

133

2. Пластинка тонкая

бесконечно длинная, намагниченная

по ширине. Положим,

что

параллельно земной поверхности рас-

положена порода

форме тонкой пластинки

под

углом

φ к

вер-

тикали

00' (рис. 64),

намагниченность

которой совпадает

со

стороной

ab = /

прямоугольника

поперечном сечении пла-

стины.

При однородной намагниченности

на

верхней

нижней

по-

верхностях пластины появятся магнитные заряды

поверхно-

стной плотностью

/, и на

каждую единицу длины

ве-

личина этого заряда

т,

оче-

видно, будет:

m=J-be.

Тогда магнитная масса

mdy,

сосредоточенная

в ка-

кой-либо точке

Q, где dy—

элемент длины пластины,

создает

любой точке про-

странства

магнитное поле,

напряженность которого

бу-

дет:

Рис.

64. К

решению задачи

нахож-

дении

поля

над

бесконечно длинной

тонкой

пластинкой.

где

— расстояние между

элементарной массой

точ-

кой

Р.

Составляющие

по

осям

координат

dX, dY, dZ

выра-

зятся путем умножения

на

соответствующие косинусы углов

между

PQ и

осями координат.

Проведем

ось χ

через точку

перпендикулярно

длине

пластинки,

ось ζ

направим вертикально,

начало координат

поместим

какую-либо точку верхней поверхности пластинки.

Тогда координатами точки

будут

х, О и R, а

координатами

точки

будут

0, у и 0 и

поэтому

Составляющие

же

вектора

выразятся уравнениями:

(5.22)

Интегрируя

эти

выражения

пределах

от

—сю

до

+оо,

полу-

чим:

(5.23)

134

Магнитное поле

тел

[Гл.

Эти уравнения показывают,

что

магнитное поле бесконечно

длинной заряженной

или

однополюсной линии

не

зависит

от

координаты

у,

параллельной этой линии.

Такие

же

выражения

для Я и Ζ мы

будем иметь

и от

ниж-

ней поверхности пластинки, координаты которой будут:

—

l sin

φ,

/?!

+/cos

φ.

Следовательно, магнитное поле всей пластинки определится

соотношениями

для Η и Ζ.

имеющими

вид:

(5.24)

При вертикальном положении пластинки, когда

φ = 0.

(5.25)

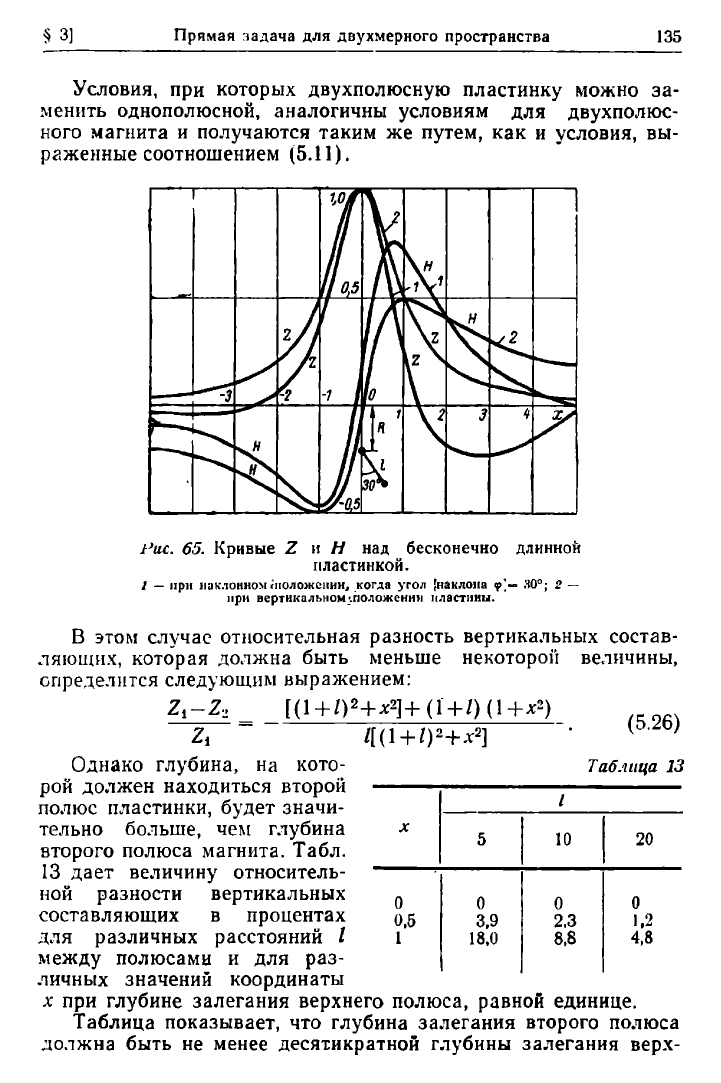
Графики, соответствующие уравнениям

(5.24)

(5.25),

пред-

ставлены

на

рис.

65.

Максимальное значение

и Z

для

однополюсной линии,

как

это

вытекает

из

уравнения

(5.25),

будет:

т.

е.

максимум

Ζ в два

раза больше максимума

Н.

Как двухполюсный магнит (схематический) является про-

межуточным геометрическим образом между однополюсным

магнитом

диполем,

так и

тонкая пластинка, которую можно

назвать двухполюсным линейным магнитом, является промежу-

точным геометрическим образом между линейным полюсом

дипольной нитью, эквивалентным цилиндру, намагниченному

по

диаметру. Действительно,

при /,

стремящемся

бесконечности,

мы имеем поле однополюсной нити

или

линии.

При /,

стремя-

щемся

нулю, формулы

(5.24)

(5.25)

переходят

формулы

для цилиндра. Чтобы показать

это,

достаточно лишь привести

уравнения

(5.24)

(5.25)

общему знаменателю

положить

полученных выражениях

/ = 0 и mdl = μ.

Прямая задача для двухмерного пространства

135

Условия, при которых двухполюсную пластинку можно за-

менить однополюсной, аналогичны условиям для двухполюс-

ного магнита и получаются таким же путем, как и условия, вы-

раженные соотношением (5.11 ).

Рис. 65. Кривые Ζ и Η над бесконечно длинной

пластинкой.

/ — при наклонном (положении, когда угол {наклона φ'·= 30°; 2 —

при вертикальномшоложении пластины.

В этом случае относительная разность вертикальных состав-

ляющих, которая должна быть меньше некоторой величины,

определится следующим выражением:

(5.26)

Таблица 13

Однако глубина, на кото-

рой должен находиться второй

полюс пластинки, будет значи-

тельно больше, чем глубина

второго полюса магнита. Табл.

13 дает величину относитель-

ной разности вертикальных

составляющих в процентах

для различных расстояний /

между полюсами и для раз-

личных значений координаты

при глубине залегания верхнего полюса, равной единице.

Таблица показывает, что глубина залегания второго полюса

должна быть не менее десятикратной глубины залегания верх-

5 10 20

0,5

3,9 2.3

1.2

18.0 8.8

4,8

136

Магнитное поле тел

[Гл. V

него,

чтобы можно было считать пластинку однополюсной, до-

пуская при этом относительную погрешность в определении Ζ

порядка 6—8%.

3. Эллиптический цилиндр, бесконечно длинный, намагни-

ченный вдоль большой оси эллипса представляет собой эллип-

соид, одна из осей которого бесконечно велика. Рассмотрим

случай, когда большая ось эллипса в сечении вертикальна,

а направление намагниченности совпадает с этой осью. Магнит-

ный потенциал эллипсоида, у которого одна из осей, например

а, равна бесконечности,-согласно теории потенциала (теорема

Маклорена), выразится

(5.27)

так как

Û=ÎH,

то Ni будет иметь вид (§ 5, гл. I, т. I)

(5.28)

Интегрирование производится подстановкой

которое дает

при этом, как и раньше, bi и с

определяются из уравнений:

Подставляя значение Ni в уравнение

(5.27),

получим

где μ — магнитный момент единицы длины эллиптического ци-

линдра

Путем несложных операций дифференцирования потенциала

получаются следующие значения составляющих напряжен-

ности магнитного поля:

(5.29)

где

t = 1(y2 +

z*-q

)

+ly*q*;

Ь?= |

(yz+z*-q

)

± |,

Прямая задача для двухмерного пространства 137

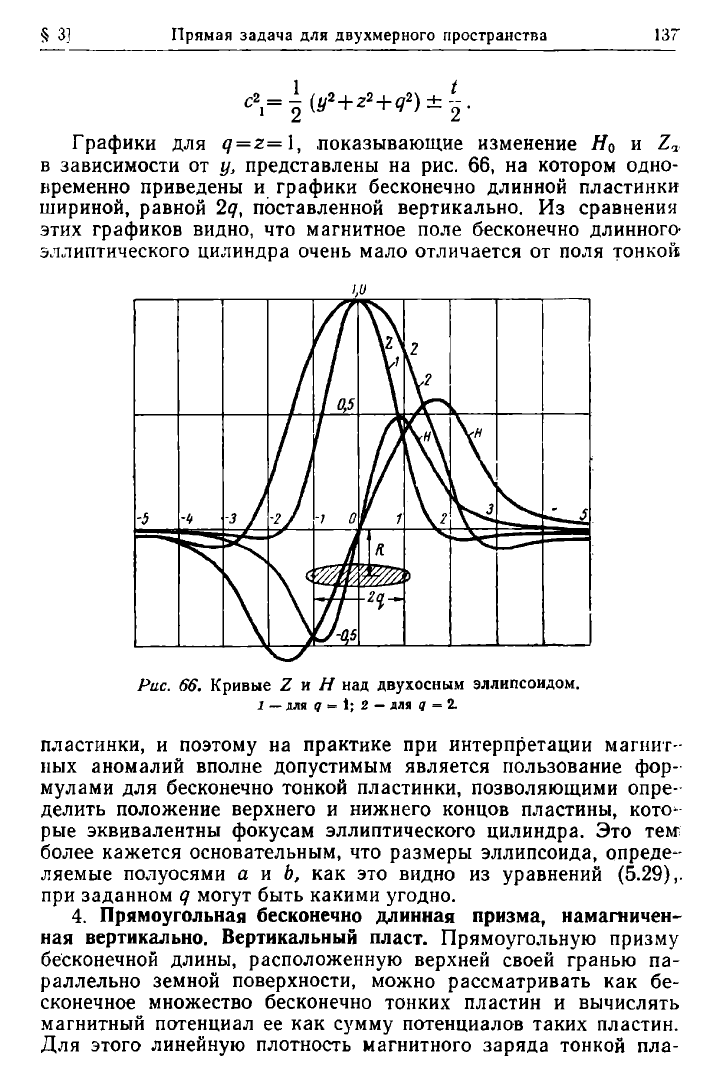
Графики для q = z=\, показывающие изменение Я

и Ζ

в зависимости от у, представлены на рис. 66, на котором одно-

временно приведены и графики бесконечно длинной пластинки

шириной, равной 2<7, поставленной вертикально. Из сравнения

этих графиков видно, что магнитное поле бесконечно длинного-

эллиптического цилиндра очень мало отличается от поля тонкой

Рас. 66. Кривые Ζ и Η над, двухосным эллипсоидом.

1 — для q

—

1; 2

—

для q = 2.

пластинки, и поэтому на практике при интерпретации магнит-

ных аномалий вполне допустимым является пользование фор-

мулами для бесконечно тонкой пластинки, позволяющими опре-

делить положение верхнего и нижнего концов пластины, кото^

рые эквивалентны фокусам эллиптического цилиндра. Это тем;

более кажется основательным, что размеры эллипсоида, опреде-

ляемые полуосями a и Ь, как это видно из уравнений

(5.29),.

при заданном q могут быть какими угодно.

4. Прямоугольная бесконечно длинная призма, намагничен-

ная вертикально. Вертикальный пласт. Прямоугольную призму

бесконечной длины, расположенную верхней своей гранью па-

раллельно земной поверхности, можно рассматривать как бе-

сконечное множество бесконечно тонких пластин и вычислять

магнитный потенциал ее как сумму потенциалов таких пластин.

Для этого линейную плотность магнитного заряда тонкой пла-

138

Магнитное поле

тел

[Гл.

стины необходимо представить

как

произведение поверхностной

плотности магнетизма

в,

сосредоточенного

на

верхней грани,

на

ширину пластины

dx,

которая бесконечно мала. Тогда, распо-

ложив

оси

координат

таком

же

направлении,

как это

имело

место

предыдущем случае, горизонтальная

вертикальная

составляющие магнитного поля, создаваемого зарядами верх-

ней грани призмы, выразятся следующими интегралами:

(5.30)

где х

—абсцисса точки

Р, в

которой рассматривается поле;

-X

—

абсцисса элемента длины

dx и 2а —

ширина призмы.

Интегрирование дает:

(5.31)

Если провести

из

точки

радиусы-векторы

и г

ребрам

призмы

(рис. 67) и

обозначить углы, составляемые

ими с

осью

ζ,

через

αϊ и а

, то из

чертежа легко видеть,

что

Следовательно,

(5.32)

тде

α —

угол,

под

которым видна

из

точки

верхняя грань

призмы.

Очевидно,

что

заряды нижней грани призмы дадут аналогич-

ное поле,

составляющие

его

выразятся такими

же

формулами,

в которые вместо расстояния

войдет расстояние

Ri до

нижней

грани. Поэтому выражение

для Я и Ζ от

всей призмы примет

вид:

(5.33)

где значения

, г

и β

видны

из

рисунка.

Если продольные размеры призмы велики

по

сравнению

глубиной залегания верхней грани,

то

влиянием нижней грани

:можно пренебречь.

таком случае магнитное поле будет опре-

Прямая задача для двухмерного пространства

139

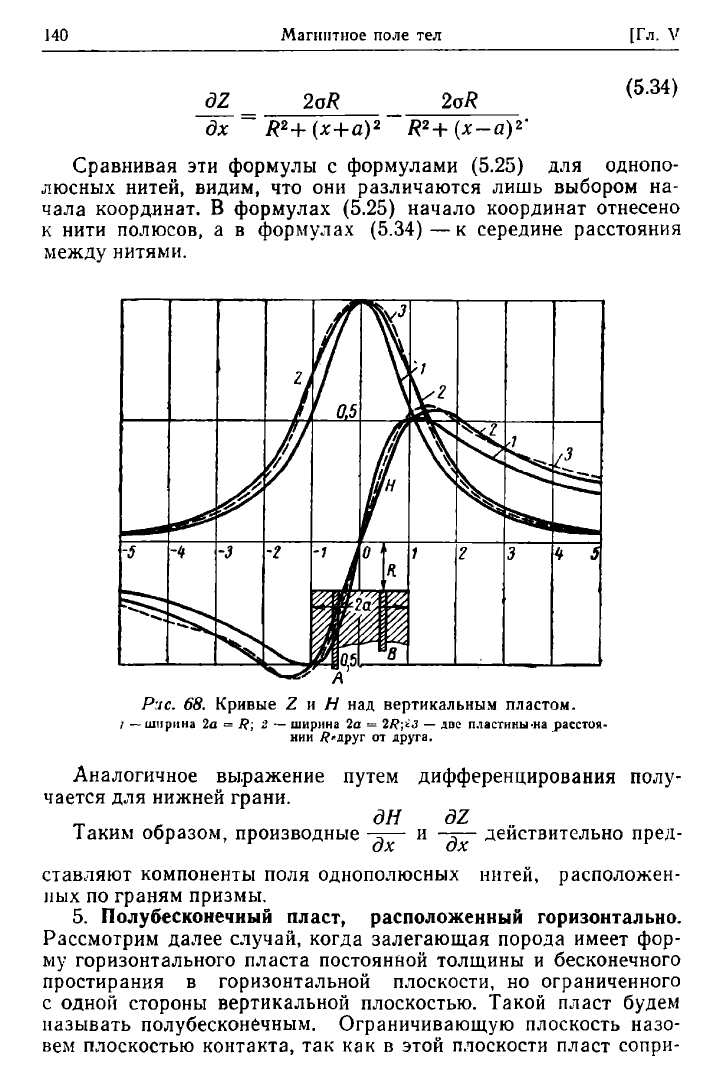
деляться формулами {5.32), графики которых представлены на

рис.

68. Графики приведены для двух случаев, когда ширина

призмы равна глубине ее -залегания и когда ширина в два раза

больше глубины. Графики показывают, что ход кривых H w Ζ

у призмы, ширина которой равна глубине залегания, почти со-

впадают с кривыми для тонкой пластинки, и расхождение за-

метно лишь для ширины призмы, равной удвоенной глубине

залегания призмы. Отношение

максимумов Н

и Z

близко к

0,5 и несколько возрастает с

увеличением ширины 2а. Кро-

ме того, максимум Н

сме-

щается вправо от оси ζ.

Хотя кривые Η и Ζ для

призмы представляют собой

сумму кривых Η и Ζ для тон-

кой пластинки, состоящую из

бесконечно большого числа

слагаемых, однако с погреш-

ностью, допустимой на прак-

тике,

их можно представить

как сумму конечного числа

кривых для тонких пластинок,

расположенных на конечном

расстоянии друг от друга. Так,

кривые для призмы шириной

2a=2R

мало чем отличаются от кривых, представляющих маг-

нитное поле двух пластинок, расположенных симметрично оси ζ

на расстоянии R друг от друга. Кривые, соответствующие этому

случаю, показаны в виде пунктирных линий на том же рис. 68.

Поэтому, зная кривые H и Z, полученные из наблюдений, нельзя

решить вопрос, представляют ли они собой магнитное поле

призмы или же сумму полей двух или нескольких пластинок,

если нет каких-либо указаний со стороны геологии или со сто-,

роны других геофизических методов о характере залежи.

Особенностью магнитного поля бесконечной призмы является

то,

что производные от компонентов И и Z, взятые по перемен-

ной х, представляют собой компоненты Н\ и Z\ поля #·, созда-

ваемого однополюсными нитями разных знаков, вытянутыми

вдоль ребер призмы. Поэтому магнитное поле призмы может

быть заменено полем таких нитей.

Действительно, дифференцируя по χ выражения

(5.31)

для

верхней грани, будем иметь

Рас. 67. К решению задачи о на-

хождении поля над бесконечной

призмой.

140

Магнитное

поле

тел

[Гл. V

(5.34)

Сравнивая эти формулы с формулами

(5.25)

для однопо-

люсных нитей, видим, что они различаются лишь выбором на-

чала координат. В формулах

(5.25)

начало координат отнесено

к нити полюсов, а в формулах

(5.34)

— к середине расстояния

между нитями.

Рис. 68.

Кривые

Ζ η H над

вертикальным

пластом.

/ — ширина 2а = R; 2 — ширина la =

2R;i3

— две пластины на расстоя-

нии У?*друг от друга.

Аналогичное выражение путем дифференцирования полу-

чается для нижней грани.

дН dZ

Таким образом, производные и действительно пред-

ставляют компоненты поля однополюсных нитей, расположен-

ных по граням призмы.

5. Полубесконечный пласт, расположенный горизонтально.

Рассмотрим далее случай, когда залегающая порода имеет фор-

му горизонтального пласта постоянной толщины и бесконечного

простирания в горизонтальной плоскости, но ограниченного

с одной стороны вертикальной плоскостью. Такой пласт будем

называть полубесконечным. Ограничивающую плоскость назо-

вем плоскостью контакта, так как в этой плоскости пласт сопри-