Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

Problems
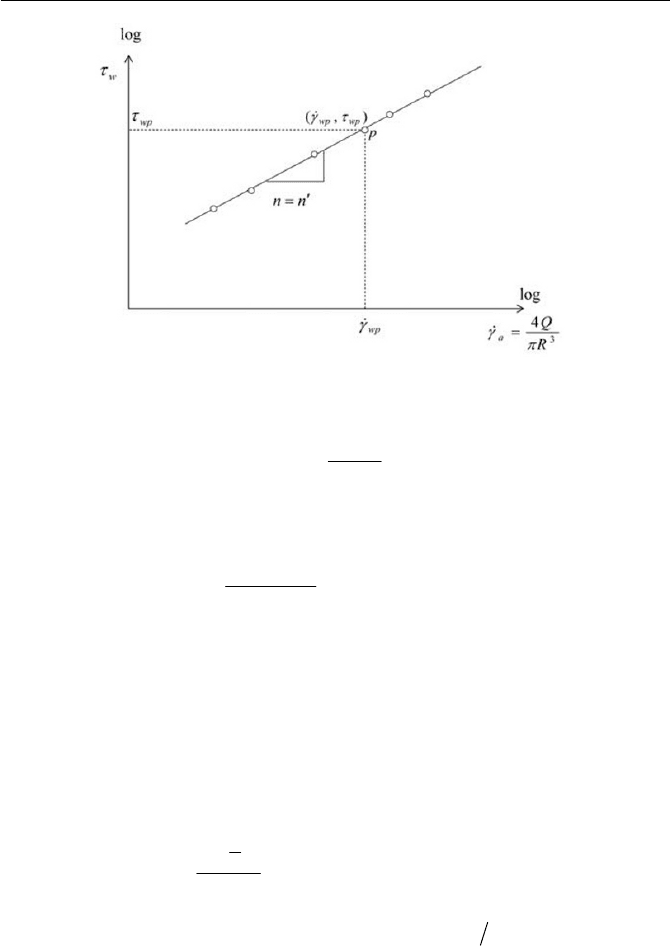
Fig. 7.14 Flow curve of power law fluid
¿
¾
½
¯
®
wpwp
n
n
nm
JW
)(
4
13
lnlnln
(22)
so that
n
wp
wp
n
n
m
°
¿
°
¾
½
°
¯
°
®
J
W
13
4
(23)
Thus, knowing
m and n in Eq. (18), the non-Newtonian viscosity
K
will
be obtained readily by the relationship given in Eq. (17).
Problems
7.2-1 In Exercise 7.2.1, show that
1
N can be further simplified to the form
1
1
|
r
k
p
N
when the inertial term is ignored. Note that
rr
kk | 11ln )( and
rrrr
kkkk | 12111
2
for 1|
r
k .
7.2-2 A power law fluid is flowing in a pipe with a 0.05 m diameter at a
'
volume flow rate of
sm /.
34
1010
u
. If the power law index
n
is 0.7,
445
7 Non-Newtonian Fluid and Flow
estimate the apparent shear rate and show the difference if the flow
is assumed to be Newtonian.
Ans.
>@
>@
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
¸
¸
¹
·
¨
¨
©
§
uu
u
u
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
¸
¸
¹
·
¨
¨
©
§
uu
u
u
s
w
s
w
1
8150
3
2
050
4
10104
14
113
fluidNewtonian
1
9020
3
2
050
4
10104
704
1703
fluidlawPower
.
.
.
.
.
.
.
.
S
J
S
J
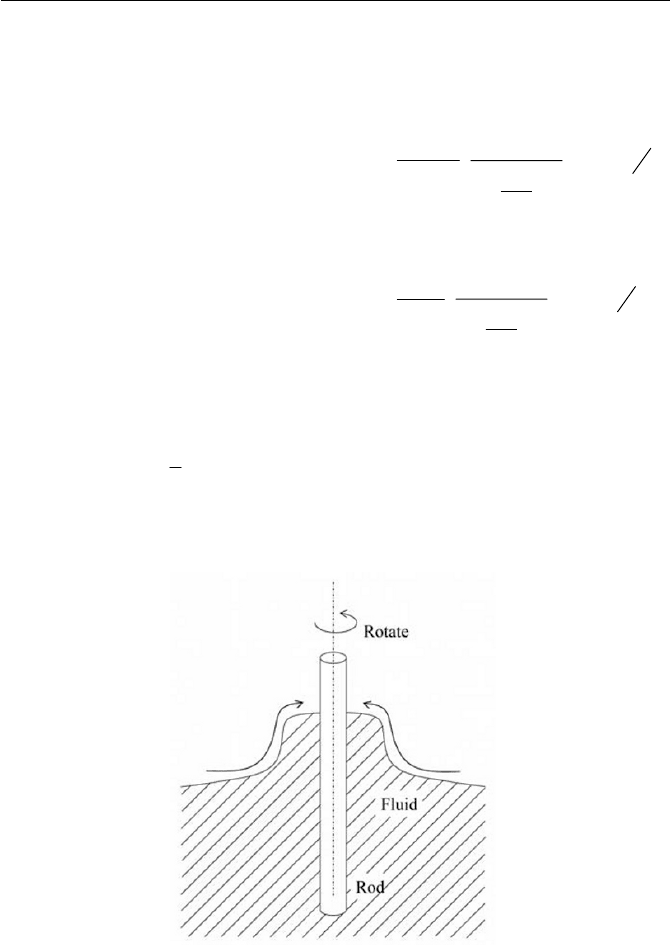
7.2-3 When a rod is rotated at an interface of a viscoelastic fluid, the fluid
climbs the rod (see Fig. 7.15). The phenomenon is called the Weis-
senberg effect. Explain this phenomenon, considering the pressure
difference
p given in Eq. (8) in Exercise 7.2.1 (cylindrical Couette
flow). Thoughts on viscoelastic phenomena would be great help,
where details will be studied in Section 7.3.
Fig. 7.15
W
Weissenberg effect
'
446

7.3 Viscoelastic Fluid and Flow
7.2-4 Discuss and specify difficulties for measuring the elongational vis-
cosity by utilizing the converging channel (refer Fig. 7.13 (b)).
7.3 Viscoelastic Fluid and Flow
There are flow phenomena that cannot be explained by the Newtonian vis-
cous law. Of which, the best know is the Weissenberg effect, in Problem
7.2.3, where some non-Newtonian fluids climb up a rod when it is inserted
perpendicular to the fluid interface and rotated along its axis. The phenom-
ena can be seen easily by stirring paint or cream in daily life. Another phe-
nomenon associated with behavior of non-Newtonian fluids is the extru-
date (die) swell in which the fluid emerges from a capillary tube and the
diameter increases in vicinity of the exit (for example see Fig. 7.13(a)).
This phenomenon is often experienced in the extrusion of meltplastic.
These phenomena of non-Newtonian fluids are responsible for normal
stress effects, contrary to what the Newtonian viscous effect (shear stress)
does. The normal stress effects are an expression of a fluid elasticity,
which is added to the viscous effects when the fluid is in motion. The vis-
coelastic fluids possess both viscous and elastic characters, with a nature
unto themselves.
There are so many attempts to include the elastic effect in a macro-
scopic constitutive equation, with which unique phenomena of viscoelastic
fluids would be explained. Although it is almost impossible to categorize
the viscoelastic constitutive equation, historically, there might be three ap-
proaches to construct the equations: the first approach is one that is devel-
oped from a simple one dimensional rheological equation using a spring
and a dashpot together with the concept of continuum mechanics, based on
experimental facts and, moreover, experiences; the second approach is one
that is derived from the general concept of genuine continuum mechanics;
and the third approach is one that is developed from molecular dynamics
in combination with the continuum concept, considering the molecular
structures of the fluids, chiefly for polymeric fluids. In this text we shall
follow the first approach in great detail.
The application of a constitutive equation for viscoelastic fluids to flow
phenomena is another problem. Particularly, flows in actual engineering
are very complicated where, in analysis, the nonlinear constitutive equa-
tion is highly coupled with its continuity, the linear momentum and energy
equations. In such situations, the only possible way to tackle these prob-
lems is to rely on numerical analysis. Nevertheless, there are some analyti-
cal solutions possible for a simple geometry of flow. In this text we will
447

7 Non-Newtonian Fluid and Flow
see some of these simple flows of viscoelastic fluids, which are described
with linear viscoelastic models.
7.3.1 Linear Viscoelastic Rheological Equations
For a linear viscoelastic rheological equation, the constitutive equation is
generally expressed by Eq. (7.1.13) with a linear relationship between
W
,
J
and their time derivatives.
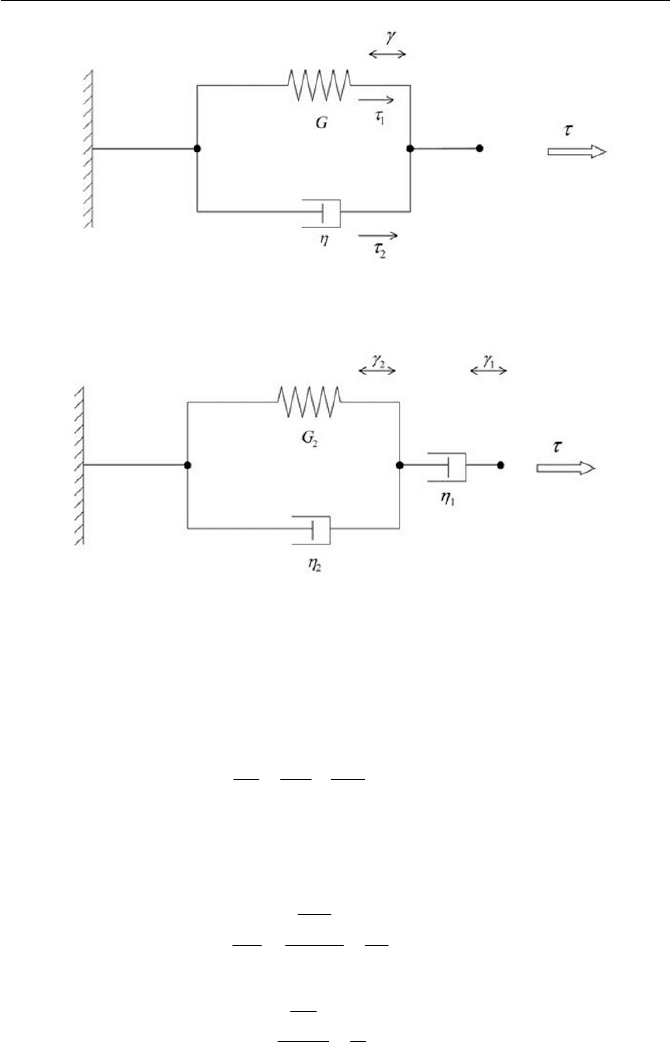
The most fundamental theory in the case of an elastic liquid is derived
from the so-called Maxwell element, as schematically shown in Fig. 7.16.
The model consists of a series arrangement of a purely viscous element as-
signed as dashpot, where
K
is the viscosity and a perfectly elastic body is
assigned as a spring where G is the modulus. The Maxwell model of vis-
coelasticity is obtained by thought of the Maxwell element, which is sub-
jected to a sudden elongation and the force is then calculated as a function
of time. As seen from the mechanical assembly in Fig. 7.16, the Maxwell
element has no unique reference length and it will deform indefinitely
when a force (per unit area)
W
is applied. This behavior is analogous to the
liquid-like behavior of a melt of an uncross-linked polymeric material over
its glass transition.
Assume that the stress
1
W
, (the force per unit area) in the spring is
1
J
G
and the stress
2
W
in the dashpot is
22
)(
J
K
J
K
ww t , Here, we have a rela-
tionship between
1
W
and
2
W
where
21
WWW
(7.3.1)
since these are connected in series. In the system where the total strain of
the system is written as
Fig. 7.16 Maxwell element
448
7.3 Viscoelastic Fluid and Flow
Fig. 7.17 Voigt element (or Kelvin element)
Fig. 7.18 Jeffreys element
21
JJJ
(7.3.2)
By differentiating Eq. (7.3.2) with respect to time t, we have
ttt w
w
w
w
w
w
21
J
J
J
(7.3.3)
so that with Eq. (7.3.1), we are able to write an equation relating the stress
and strain rate
K
W
W
K
W
W
J
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
w
w
G
t
G
t
t
2
1
(7.3.4)
449
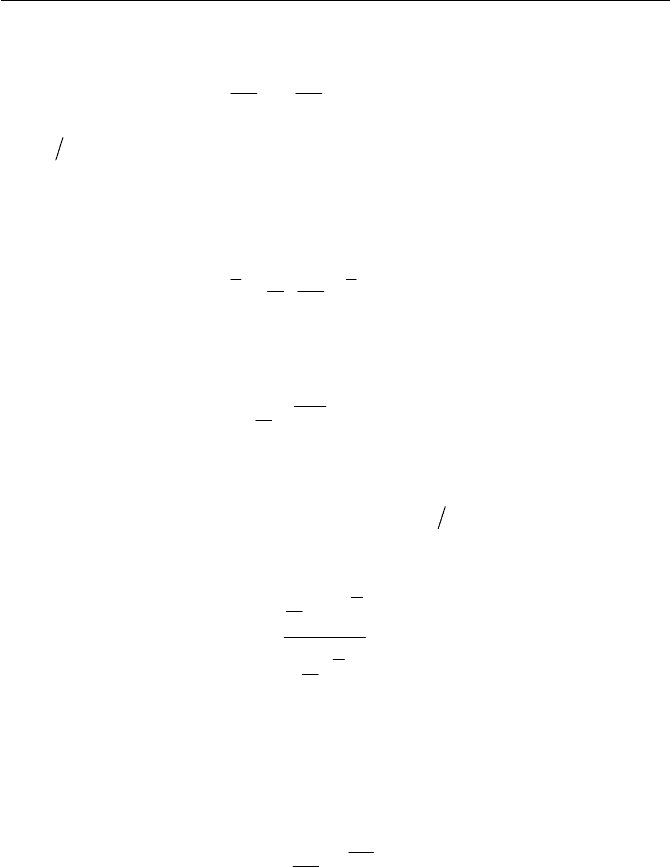
7 Non-Newtonian Fluid and Flow
Equation (7.3.4) can be further reduced as an expression for
W
where
tt w
w
w
w
J
K
W
OW
(7.3.5)
G
K
O
is called the relaxation time. Equation (7.3.5) is the Maxwell
model of a viscoelastic fluid. Equation (7.3.5) is a first order ordinary dif-
ferential equation of
W
. Since
W
is only a function of time, Eq. (7.3.5) can
be solved for
W
to give
»
¼
º
«
¬
ª
c
¸
¹
·
¨
©
§
c
w
w
³
c
ctde
t
e
tt
OO
J
O
K
W
and using
J
''
'
dtte
t
tt
J
O
K
W
O
³
f
»
»
¼
º
«
«
¬
ª
(7.3.6)
where the stress
W
at f t is determined to have a finite value
f
W
for the finite value of the strain rate
f
w
t
t
J
J
at f t , i.e. to
satisfy the following condition
f
fofo
JK
O
J
O
K
W
O
O
t
t
tt
e
et
t
1
limlim
(7.3.7)
It should be mentioned that Eq. (7.3.5) is the differential equation for the
Maxwell model and Eq. (7.3.6) is the integral equation for the Maxwell
model, both of which are equivalent. Equation (7.3.6) can be further re-
duced to the following expression with the integration by parts where
³
f
c
cc
°
¿
°
¾
½
°
¯
°
®
t
tt
tdttet
-
2
),(
)(
J
O
K
W
O
(7.3.8)
In Eq. (7.3.8), we used the strain at a past time
t
c
relative to the reference
a unique configuration for the fluid at time past, but with only a reference
state at the present time. Thus, the relationship between the strain and
strain rate will be given where
state at the present time
t
. This is due to the reason that there would not be
450

7.3 Viscoelastic Fluid and Flow
³
c
c
t
t
duutt
JJ
,
Equivalently,
³
c
c
w
w
c
c
w
w
c
t
t
duu
t
tt
t
t
JJJ
,
(7.3.9)
The mechanical assembly that consists of a spring in parallel with a
dashpot is called a Voigt (or Kelvin) element, or body, as schematically
displayed in Fig. 7.17. The schematic of the assembly is where the body
returns to a unique length, to the rest of the length of the spring, when the
force (per unit area) is absent. The Voigt element is not intended to be a
model for an elastic rubber; however, qualitative characteristics are quite
similar to those exhibited by rubbers for its response to changes in applied
force, showing that the Voigt element is analogous to the behavior of a vis-
coelastic solid.
With Voigt element, the strain
J
is the same at both of the spring and
dashpot, besides for the overall force (per unit area)
W
of the parameter as-
sembly, we can write
21
WWW
(7.3.10)
so that the following relationship exists
t
G
w
J
KJW
(7.3.11)
Equation (7.3.11) is the Voigt model of a viscoelastic solid and can be solved
for
t
J
with an initial condition of
0
WW
and 0
H
at time 0 t , to yield
¸
¸
¹
·
¨
¨
©
§
t
G
e
G
K
W
J
1
0
(7.3.12)
The important point of the model is that the viscous resistance to elonga-
tion brings a time dependency into the response of the body. Equation
(7.3.12) may be alternatively written in the following form, by setting
G
KO
and G
0
WJ
¸
¸
¹
·
¨
¨
©
§
O
JJ
t
e1
(7.3.13)
451

7 Non-Newtonian Fluid and Flow
This indicates that for a sudden change in force (per unit area)
0
W
, the
strain
J
approaches its plateau
J
asymptotically as time elapses. This
indicates that a viscoelastic solid has a time constant
O
and cannot re-
spond instantaneously to changes in stress. This is called the retarded elas-
ticity, and the time to reach
e1 of
J
is called the retardation time. The
strain change
t
J
in time
t
for a given stress
0
W
is called the creep.
While dealing with more realistic viscoelastic materials, the basic
models (i.e. the Maxwell element and Voigt element) are not necessarily
adequate to apply with their own form. There are typically some combina-
tions of these mechanical assemblies, and along which are the three ele-
mental models of viscoelastic liquids called the Jeffreys elements, as indi-
cated in Fig. 7.18. For the three elements models, we have the following
stress-strain relations
tw
w
1
1
J
KW
(7.3.14)
t
G
w
w
2
222
J
KJW
(7.3.15)
From Eqs. (7.3.14) and (7.3.15), we can write an expression after differen-
tiating both sides
2
2
2121212
t
t
G
t
G
w
w
w
w
w
w
J
KK
J
K
W
KKW
(7.3.16)
By knowing that
W
and
J
are functions of time only, we can write Eq.
(7.3.16) with the simple form
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
tt
b
t
b
t
a
JJW
W
211
(7.3.17)
where
1
a
,
1
b
and
2
b
are the new constants defined where
2
21
1
G
a
K
K
,
11
K
b and
2
21
2
G
b
K
K
(7.3.18)
The three new constants have relationships:
2
1
1
2
1
Gb
b
a
K
(7.3.19)
452

7.3 Viscoelastic Fluid and Flow
and
1
2
1
b
b
a
!
(7.3.20)
Herewith, both
1
a
and
12
bb
have a unit of time where we can replace
them with new notations
11
O
a and
2
1
2
O
b
b
(7.3.21)
Using
1
O
and
2
O
, Eq. (7.3.17) can be rewritten where
¸
¹
·
¨
©
§
w
w
w
w
tt
J
OJK
W
OW
201
(7.3.22)
with
10
b
K
and
21
OO
! . Equation (7.3.22) is a constitutive equation of the
Jeffreys model that contains two time constants
1
O
and
2
O
; these are re-
laxation time constant and retardation time constant, respectively.
Since
W
is a function of only time, Eq. (7.3.22) is a first order ordinary
differential equation and there is a solution via an integral form as follows
tdtttet
t
tt
cc
°
¿
°
¾
½
°
¯
°
®
c
¸
¸
¹
·
¨
¨
©
§
³
f
¸
¸
¹
·
¨
¨
©
§
c
JG
O
OK
O
O
O
K
W
O
1
20
1
2
1
0
2
1
1
(7.3.23)
where
t
G
is the Dirac delta function. Equation (7.3.23) can be further re-
duced to the following form with an integration by parts
tdttttet
t
tt
cc
°
¿
°
¾
½
°
¯
°
®
c
c
¸
¹
·
¨
©
§
³
f
¸
¹
·
¨
©
§
c
JG
O
OK
O
O
O
K
W
O
1
20
1
2
2
1
0
2
1
1
(7.3.24)
where we used following relationship of the delta function
02
0
fdtxxfdxxxf
aa
a
³³
GG
(7.3.25)
and
0fdxxxf
a
a
c
c
³
)()(
G
(7.3.26)
Experiments thought of vis a vis the Maxwell element, Voigt body and
Jeffreys model are subjected to a sudden unidirectional elongation in
453

7 Non-Newtonian Fluid and Flow
which the forces (per unit area) are calculated as a function of time. The
analogous rheological experiment is one in which a sample of viscoelastic
material is suddenly deformed:
0
J
at time 0 t , and then the resulting
stress
t
W
is measured as a function of time, that is
00
J
J
W
,tGt
(7.3.27)
0
J
,tG is called the relaxation modulus. This is called a stress relaxation
experiment. As the most fundamental point of correspondence, we will
now show that for a very small strain
1
0
J
, G is independent of
0
J
in
general, so that a linear relationship may stand, such that
0
J
W
tGt
(7.3.28)
This very small-strain behavior is called a linear viscoelasticity.
A general equation that describes all types of linear viscoelastic behav-
ior may be derived from the idea of a superposition principle, called the
Boltzmann’s superposition principle as shown in Fig. 7.19. Consider a se-
quence of a very small strain occurring at time
1
t
,
2
t
,
3
t , so that we have
the relationship, according to the principle
ᇫ
ᇫᇫᇫᇫ
tttG
tttttG
tttGtttGt
t
t
Ni
i
i
cc
|
!
}
³
¦
GJ
GJ
G
J
G
J
W
N
1
2211
(7.3.29)
For an interval of a step strain
t
c
GJ
, we may write
tdt
c
c
JGJ
, so
that Eq. (7.3.29) can be rewritten where
ttGt
t
c
³
f
JW
(7.3.30)
It is noted that
f
W
is defined by a mathematical convenience, with
reference to Eq. (7.3.7), so that the stress
W
has a finite value at f t .
Equation (7.3.30) can be further reduced to another expression in terms of
the strain
J
(instead of the strain rate
J
) vis a vis the integration by parts,
using the relationship of Eq. (7.3.9), as follows
c
td
454
