Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

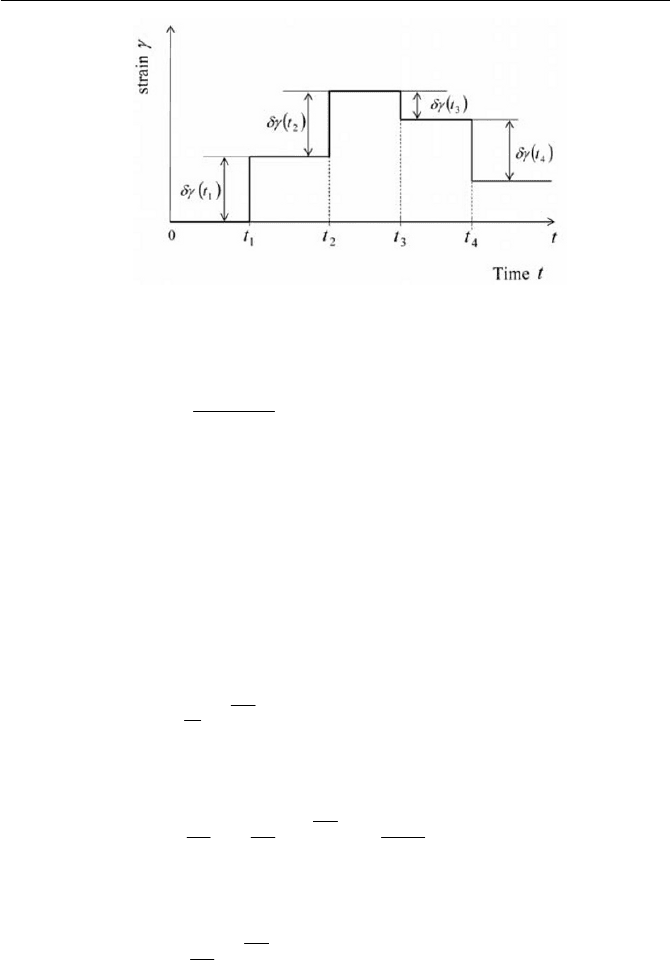
7.3 Viscoelastic Fluid and Flow
Fig. 7.19 Step strain in superposition principle
³
³
f
f
cc
cc
w
c
w
t
t
tdttttM
tdtt
t
ttG
t
,'
,
'
J
JW
(7.3.31)
'ttM is called the memory function. Both integral expressions in Eqs.
(7.3.30) and (7.3.31) show that the stress at the present time
t depends on
the history of the state of the strain for all times past
.tt d
c
f
In summarizing this section, let us look at the linear viscoelastic fluids
relaxation modulus where the Maxwell model and the Jeffreys model are
respectively given as
¸
¹
·
¨
©
§
c
O
O
K
'tt
ettG
(7.3.32)
and
ttettG
tt
c
¸
¸
¹
·
¨
¨
©
§
c
¸
¸
¹
·
¨
¨
©
§
c
G
O
OK
O
O
O
K
O
1
20
1
2
1
0
21
1
(7.3.33)
Similarly, the memory functions are respectively given where
¸
¹
·
¨
©
§
c
c
O
O
K
tt
ettM
2
(7.3.34)
and
455

7 Non-Newtonian Fluid and Flow
ttettM
tt
c
c
¸
¹
·
¨
©
§
c
¸
¹
·
¨
©
§
c
G
O
OK
O
O
O
K
O
1
20
1
2
2
1
0
2
1
1
(7.3.35)
It is mentioned that the exponential factors in
G and
M
describe the
fading memory, which is the decay of a weighting factor (both the relaxa-
tion modulus and the memory function) as time elapses from its original
state.
7.3.2 Linear and Nonlinear Viscoelastic Models
Linear viscoelastic rheological equations can now be generalized to ar-
bitrary small displacement flows, recognizing, first of all, that the relaxa-
tion process is independent, not only of the magnitude of the strain
J
, but
also of kinematics of the deformation. This can be done by replacing the
strain
J
by the strain tensor Ȗ and the strain rate
J
by the rate of the
strain tensor
Ȗ
for infinitesimal deformations. In addition, the stress
W
to
achieve via the stress tensor
IJ is used to obtain the following alternative
forms of the Boltzmann’s superposition principle:
³
f
ccc
t
tdttttGt ,ȖIJ
(7.3.36)
and
³
f
ccc
t
tdttttMt ,ȖIJ
(7.3.37)
Then the Maxwell model is written via integral equation
tdttet
t
tt
cc
»
»
¼
º
«
«
¬
ª
³
f
¸
¹
·
¨
©
§
c
,ȖIJ
O
O
K
2
0
(7.3.38)
Equivalently, with use of a differential equation, we have
Ȗ
IJ
IJ
0
KO
w
w
t
(7.3.39)
Similarly, the Jeffreys model is also written as an integral equation,
giving us
456

7.3 Viscoelastic Fluid and Flow
tdttttet
tt
t
cc
»
¼
º
c
c
¸
¸
¹
·
¨
¨
©
§
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
c
f
³
,ȖIJ
G
O
OK
O
O
O
K
O
1
20
1
2
2
1
0
2
1
1
(7.3.40)
Again, an equivalent form via a differential equation:
¸
¹
·
¨
©
§
w
w
w
w
tt
Ȗ
Ȗ
IJ
IJ
201
OKO
(7.3.41)
In Eqs. (7.3.38) to (7.3.41), we used
0
K
as the zero shear rate viscosity.
These linear viscoelastic constitutive equations derived from general-
ized Maxwell and Jeffreys models are based on the idea that flows undergo
infinitesimal displacement gradients. However, flows with large displace-
ment gradients are found to be more realistic in practice, and constitutive
equations are obtained on the basis of large displacement gradients that are
found to be more appropriate in comparison with experiments. Also, some
molecular theories, such as Bird et al., (1987 vol. 2), suggest very strongly
that it is more appropriate to adopt the concept of large displacement gra-
dients. Owing to these reasons, it is thought to take a fairly large displace-
ment gradient into consideration in order to construct a viscoelastic consti-
tutive equation.
An admissible viscoelastic constitutive equation would be obtained
from a thought of relative strain tensor
IC,Ȗ
c
1
tt
R
given in Eq. (1.4.6),
where
1
C
is the Finger tensor.
R
Ȗ
, a symmetric tensor, contains informa-
tion about the orientations of the three principle axes of stretch ratios and
the magnitudes of the three principle stretch ratios. It should be kept in
mind, as verified in Section 1.4, that
1
C
itself does not contain informa-
tion about the rotation of material lines that occurs during the deformation.
With the argument introducing the relative strain tensor
R
Ȗ
in a viscoe-
lastic constitutive equation, we shall replace
tt
c
,Ȗ
in Eq. (7.3.37) with
tt
R
c
,Ȗ
, to give
³
³
f
f
ccc
c
c
t
R
t
tdttttM
tdttMt
),(Ȗ
ICIJ
1
(7.3.42)
The model of Eq. (7.3.42) is referred to as a Lodge network (rubberlike)
liquid and has a linear dependence on the history of a relative strain tensor,
although a relative strain tensor is itself nonlinear in the displacement gradi-
ents. In this sense, the model may be regarded as quasi-linear. By adopting
457
7 Non-Newtonian Fluid and Flow
the memory function
ttM
c
from the Maxwell model given in Eq.
(7.3.34), we have a constitutive equation when writing
tdttet
R
t
tt
cc
»
»
¼
º
«
«
¬
ª
³
f
¸
¹
·
¨
©
§
,ȖIJ
'
O
O
K
2
(7.3.43)
A simple integral constitutive equation of a nonlinear version, such as
Equation (7.3.43), can be converted to an equivalent differential form by
differentiating the equation via the present time
t . The time dependent
term appears in the integral in three places; they are: in the memory func-
tion, in the Finger tensor, and in the upper limit of integration. Now we can
see the conversion of the integral constitutive equation of Eq. (7.3.43) into
the differential form
3
1
0
2
3
0
1
2
0
»
»
¼
º
«
«
¬
ª
cc
»
»
¼
º
«
«
¬
ª
cc
»
»
¼
º
«
«
¬
ª
c
f
¸
¹
·
¨
©
§
c
f
¸
¹
·
¨
©
§
c
c
¸
¹
·
¨
©
§
c
³
³
tdte
tdte
et
t
tt
R
t
tt
tt
tt
R
)(C
)(Ȗ
Ȗ
O
O
O
O
K
O
K
O
K
IJ
(7.3.44)
In using the following identity for the time derivative of a Finger tensor
T
T
tt
t
uu
w
w
w
w
11
11
1
1
CC
EE
C
)(C
(7.3.45)
we have a differential form of the constitutive equation where
Equation (7.3.43) is known as the Lodge equation, which is really a
nonlinear equation similar to the Maxwell model in terms of the displace-
ment gradients. In similar fashion, the specific choices for memory func-
tion, for example, the Jeffreys model given by Eq. (7.3.35), will lead to
another type of nonlinear version of the model.
458

7.3 Viscoelastic Fluid and Flow
>@
)(
)()(
IJIJIJ0IJ
3
0
3
21
2
0
1
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
T
T
uu
uu
O
K
OO
K
(7.3.46)
Each bracket…(1), (2) and (3)…implies that of Eq. (7.3.44). Rearrange-
ment of the terms in Eq. (7.3.46) yields
eIJIJ
0
2
KO
(7.3.47)
where
denotes the upper convective time derivative defined in Eq.
(1.3.13), i.e.
T
uu
IJIJIJIJ
(7.3.48)
e is the rate of the strain tensor defined in Eq. (1.1.16), i.e.
T
uu Ȗe
2
(7.3.49)
Equation (7.3.47) is called the upper convective Maxwell (UCM) equation.
As discussed in Section 1.3, the UCM equation does obey the material ob-
jectivity, equivalent for the principle of the frame invariance. Furthermore,
in view of satisfying the material objectivity, the UCM equation is ex-
tended to be written as
eIJIJ
0
2
KO
(7.3.50)
as well as
eIJIJ
0
2
KO
q
(7.3.51)
where ' and q denote the lower convective time derivative and the coro-
tational or Jaumann time derivative respectively, referring to Eqs. (1.3.14)
and (1.3.15). These equations are called, respectively, the lower convective
Maxwell (LCM) equation and the corotational Maxwell (CRM) equation.
It appears that UCM equation is more commonly used in practice than the
other two Maxwell models. This is chiefly because of the reason that the
other Maxwell model (LCM in particular) does not give a qualitative
agreement in comparison with rheological experimental data, and have no
molecular basis, while the UCM equation does gain its background from
the molecular based dynamic theories from Bird et al. (1977). The integral
'
459

7 Non-Newtonian Fluid and Flow
form of the CRM equation is often called the Goddard–Miller equation
(1966), which contains a spectrum of relaxation times.
In carrying out a numerical simulation to a flow of viscoelastic fluid,
the differential type of constitutive equation is often more preferable than
the integral type in discretizing procedure.
In similar fashion, the integral constitutive equation of the Jeffreys
model given in Eq. (7.3.40), can be converted into differential equations.
Resultantly, they are, as proposed by Oldroyd
¸
¹
·
¨
©
§
eeIJIJ
201
2
OKO
(7.3.52)
and
¸
¹
·
¨
©
§
OKO
eeIJIJ
201
2
(7.3.53)
These two equations are also frame invariants, meeting the requirements
from the material objectivity. Equation (7.3.52) is called the Oldroyd-B
equation, and Eq. (7.3.53) the Oldroyd-A equation. As mentioned earlier,
Oldroyd-A equation is not used due to the reasons inherited from the prob-
lems of LCM. In addition to the Oldroyd-A and B equations, there is an
equation, called the corotational Jeffreys equation, which has the expres-
sion
¸
¹
·
¨
©
§
q
q
eeIJIJ
201
2
OKO
(7.3.54)
Oldroyd’s equations have an additional term,
)ee,e
q
222
(or
OOO
to Max-
well’s equations, which are inherited from the retardation term of the Jef-
freys model given in Eq. (7.3.22). This term can be regarded as arising
from stresses in a solvent of polymeric solutions (denote the solvent stress
s
IJ and the polymer stress
p
IJ
). In the case of Oldroyd-B equation, the (to-
tal) stress
IJ
can be regarded as a simple summation of
p
IJ and
s
IJ as
sp
IJIJIJ
(7.3.55)
where for, with
p
IJ and
s
IJ , the following constitutive equations can be
applied:
eIJIJ
pp p
KO
2
1
(7.3.56)
and
''
'
460

7.3 Viscoelastic Fluid and Flow
eIJ
s s
K
2
(7.3.57)
Equations (7.3.56) and (7.3.57) are respectively the UCM equation and the
Newtonian viscous equation. Any constant appearing in Eqs. (7.3.56) and
(7.3.57) can be related by
sp
s
sp
KK
OK
OKKK
1
20
and
(7.3.58)
where
p
K
and
s
K
are respectively the viscosity of a polymer contribution
and a solvent viscosity. It is further noted that the Oldroyd-B model has a
molecular basis from the elastic dumbbell in a solvent. Oldroyd (1958)
proposed an extension of the B-equation, introducing 8 constants in the
equation, which are also subject to the constraints of frame invariance. The
Oldroyd 8-constant equation yields a reasonable account for estimating
non-Newtonian viscosity and normal stress differences for incompressible
viscoelastic fluids. In opposition to what has just been stated, there is a
disadvantage for a model that, at a higher shear rate, the model tends to
loose its quantitative agreement with actual experimental data.
We now look into a strongly nonlinear case, while as we have seen thus
far, the Maxwell equations and Oldroyd’s equations are, in a sense, quasi-
linear, where the stress and strain relationship is indeed linear. Giesekus
(1982) proposed a model like the UCM equation, in which a nonlinear
term, derived from the viewpoint of a molecular basis, is appended.
Namely, the constitutive equation is given where
eIJIJIJIJ
pppp
p
p
K
K
O
DO
2
1
1
(7.3.59)
with auxiliary equations written as
ps
IJIJIJ
(7.3.60)
and
eIJ
s s
K
2
(7.3.61)
Note that
p
IJ and
s
IJ are, respectively, solvent and polymer contributions
to the stress tensor IJ . The Giesekus model contains four constants, in
which
1
O
is a relaxation time,
s
K
and
p
K
are respectively the solvent and
polymer contributions to the zero-shear rate viscosity
0
K
and
D
is a non-
dimensional parameter called the mobility factor. The term involving
D
is
originally derived from a molecular theory associated with anisotropic
461

7 Non-Newtonian Fluid and Flow
hydrodynamic drag on the constituent polymer molecules, Giesekus
(1966). The model is originally designated as an application for polymer
solutions. The range of the mobility factor
D
lies between 0 and 1, where
0
D
corresponds to the minimum anisotropies (isotropic drag) where the
UCM equation is recovered, while
1
D
corresponds to the strongest ani-
sotropic drag. It is worthily mentioned that, when
1
D
, a steady state
shear and an elongational stress are identical to those obtained from CRM
equations. It appears that Eq. (7.3.59), the polymer contribution constitu-
tive equation, is found to give a good rheological characterization to poly-
mer melts.
Equations (7.3.59), (7.3.60) and (7.3.61) can be converted to a single
constitutive equation with the following relationship
eIJ
p s
K
2 IJ
(7.3.62)
which is substituted in Eq. (7.3.59) to give
¸
¸
¹
·
¨
¨
©
§
eeee
eIJIJeIJIJIJIJ
1
2
2
20
2
0
1
1
22
2
O
O
EOK
EO
K
O
EO
(7.3.63)
where constants have a mutual relationship to satisfy
120
120
1
and ,
OO
D
E
K
K
OOKKK
/
s
ps
(7.3.64)
It will prove useful to note that with the constitutive equation of Eq.
(7.3.63), the shear viscosity has a finite value as the shear rate
J
ap-
proaches infinity, satisfying the rheological characters of polymeric solu-
tions. The Giesekus model can be reduced to a number of constitutive
equations referred to in the literature. For example, by setting
0
2
O
and
21/
D
, the Leonov-like model (1976) of a steady shear and a shearfree
flows are reduced.
There are some useful nonlinear constitutive equations, which are
listed below.
462

7.3 Viscoelastic Fluid and Flow
eIJIJ
p
JK
JK
2
G
(7.3.65)
where
G is a constant modulus and
J
is defined as
2
1
2
1
II
2
1
2
1
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
e
Ȗ:Ȗ
J
(7.3.66)
(ii) The Phan-Thien and Tanner model (1977)
eIJIJIJ
*
0
2
KO
r
tY
(7.3.67)
*
IJ is an interpolated derivative defined by the following formula using
Eq. (7.3.63)
¿
¾
½
¯
®
¸
¹
·
¨
©
§
IJIJȦIJIJȦ
IJ
IJ
*
2
1
c
dt
d
T
(7.3.68)
and
IJIJ
IJ
r
t
r
atetY
r
1
0
K
HO
(7.3.69)
where
a , c and
H
are constants.
Y
, as a function of IJ
r
t given in Eq.
(7.3.69), is used for curve fitting for certain rheological data with
a being
a constant of small argument approximations and for
00
O
K
G .
Integral form:
(i) The convected generalized Maxwell model (Lodge network model,
1964 and 1983)
tdtte
R
t
n
i
tt
i
i
i
cc
»
»
¼
º
«
«
¬
ª
³
¦
f
¸
¸
¹
·
¨
¨
©
§
c
,ȖIJ
1
2
O
O
K
(7.3.70)
where the bracket is the memory function. The model is derived from a
molecular theory of polymer melts, and also gives a constitutive equation
for dilute polymer solutions, by giving explicit expressions for
i
K
and
i
O
.
Differential form:
(i) The White–Metzner model (1963)
'
463

7 Non-Newtonian Fluid and Flow
tdtt
W
tt
W
ttM
R
R
t
c
»
¼
º
«
¬
ª
c
w
w
c
w
w
c
³
f
,Ȗ,ȖIJ
ൖ
ൖ
,I
I
ൖI,
(7.3.71)
In Eq. (7.3.71),
W is a scalar (potential) function that gives strain energy
and
ttU
c
II,I, is the free energy of elastic deformation as follows
ൖI, ,ൖI, WttMttU
c
c
(7.3.72)
where I and II are scalars defined from the Finger tensor
1
C as follows
1
I
C
r
t
(7.3.73)
and
»
¼
º
«
¬
ª
2
2
1
2
1
ൖ CC
rr
tt
(7.3.74)
Some simplifications are expressed with an incompressible flow limit, i.e.
1det
ൗ
1
C
(7.3.75)
and with the Cayley-Hamilton theorem
CICC
ൖൕ
12
(7.3.76)
Taking the determinant to both sides, we have
C
r
t ൖ
(7.3.77)
where
C is known as the Cauchy strain tensor, defined where
ICC
1
(7.3.78)
Also, the term
R
Ȗ that appears in the second term of Eq. (7.3.71) is the
(another form of) relative strain tensor, namely
CIȖ
R
(7.3.79)
As an alternative, Eq. (7.3.71) is also written in its original form as fol-
lows:
td
ttUttU
t
R
R
c
»
¼
º
«
¬
ª
w
c
w
w
c
w
³
f
ȖȖIJ
ൖ
,ൖI,
I
,ൖI,
(7.3.80)
Equation (7.3.80) is proposed independently by Kaye (1962) and Bernstein,
et al. (1963), and is widely known as the K-BKZ equation, which is devel-
oped around ideas of rubber elastic theories.
(ii) The Factorized K-BKZ equation:
464
