Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

7.2 Standard Flow and Material Functions

By subjecting to the limit of linear viscoelasticity (such that the viscoe-

lastic material under this study may follow both Hooke’s law and New-

ton’s law simultaneously) stress is linearly dependent upon the shear strain

and the shear strain rate at any time. This is the basic idea of the Boltz-

mann’s superposition principle, and that is directly applied to developing

the mathematical modeling of liner viscoelastic materials. From the

rheometric point of view, the basic theory of linear viscoelasticity consti-

tutes a convenient and a rather accurate analytical tool to analyze rheomet-

ric experimental data. In following the principle of superposition, we can

write the shear stress

as linear in the strain or strain rate with corre-

sponding forms of Eqs. (7.2.23) and (7.2.24), assuming that the relevant

strain or strain rates are small enough



įȦtȖGĲ

 sin

(7.2.25)



 ȦtȖȘĲ

cos



(7.2.26)

where

and

are phase-shifts that are sometimes called mechanical loss

angles. Note that

G and

ȖȘ



give the stress amplitudes. Instead of

relating



Ȧį and



with material functions, it is customary to write

these relationships in the following forms, using trigonometric identity

     

ȦtȦGȦtȦGȖĲ

cossin



(7.2.27)

     

ȦtȦȘȦtȦȘȖĲ

sincos





(7.2.28)

There are two sets of linear viscoelastic material functions, namely

and

, appearing in Eqs. (7.2.27) and (7.2.28), where G

is called

the storage modulus, and

is called the loss modulus and

is called

the dynamic viscosity.

It is sometimes convenient to consider



ȦG

and



ȦG

as real and

imaginary components of a complex number respectively, defined as fol-

lows

  

ZZZ

GiGG



(7.2.29)

where

G is called the complex modulus. Thus, from Eq. (7.2.29), the

magnitude of

G is given:

 

GGG



(7.2.30)

425

7 Non-Newtonian Fluid and Flow

Furthermore, in Eq. (7.2.27),

and

are expressed in terms of a

phase-shift where



įGG

cos

and



įGG

sin

(7.2.31)

Alternatively, we may be able to define the complex viscosity



by writing

  

ȦȘiȦȘȦȘ



(7.2.32)

where

 

ȘȘȘ



As a result, we have the following relationship

ZKK

Gį

sin

and

ZKK

Gį

cos

(

7.2.33)

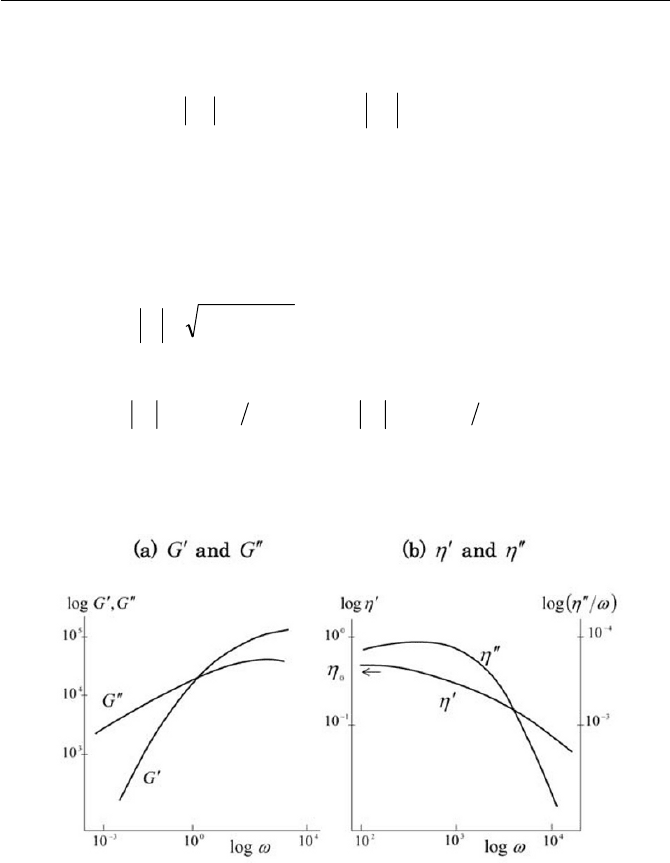
The typical trends of experimental observation on G

, G

and

are sketched for linear polymeric fluids in Fig. 7.11.

Fig. 7.11

Time dependent material functions; (a)

and

for typically

polyethylene melt; (b)

and

for a typically narrow distribu-

tion linear polymer

It will now prove useful to speculate on the limiting behavior of the

storage and the loss moduli at low frequencies as

; and at high fre-

quencies as

for linear viscoelastic fluids. At low frequencies, as

426

7.2 Standard Flow and Material Functions

expected from a linear viscoelastic fluid, we may find that viscous effects

dominate the behavior so that



limlim

(7.2.34)

0limlim

0ൺ0ൺ

(7.2.35)

0lim

(7.2.36)

where

is the zero-shear viscosity. Furthermore, it is known that

approaches a non-zero limiting value, for low frequencies







ZKZ

limlim

(7.2.37)

where

is a limiting value for 0o

At high frequencies, the elasticity effects come to dominate the behav-

ior in such a way that

lim

(7.2.38)

0limlimlim

ofofof

ZZZ

(7.2.39)

where

G is referred to as the glassy modulus; moreover,

becomes

proportional to .

2

At very high frequencies, the fluid becomes like an

elastic solid, where no viscous effects tend to appear.

There are some useful relationships involving viscometric functions to

relate time-independent and time-dependent material functions. One of the

most quoted relationships among many others is the Cox-Merz (Cox and

Mertz, 1958) rule, which is expressed as

  

ZKJK



by setting



(7.2.40)

This rule has been found to be relatively reliable for fluids with flexible

molecules, and other relationships as the ones proposed by Laun (1986) for

the first normal stress coefficient

where

 

ccc





(7.2.41)

This relationship is tested for melts of some low- and high-density poly-

mers, Laun (1986).

427

7 Non-Newtonian Fluid and Flow

7.2.4 Viscometric Flow in Rheometry

Through the determination of material functions, we have discussed vis-

cometric (or rheometric) flows that are equivalent to steady (or unsteady)

simple shear flows, such as Couette flows, and shearfree flows, such as

elongational flows. In this section, we shall pay more attention to practical

measurements that determine those material functions, specifically the vis-

cosity, the two normal stress differences, and the elongational viscosity.

The time-dependent material functions of kinematically variable vis-

cometric flows and shearfree flows may be readily established from the

time independent rheometric flows although, in practice, in precision

measurements they are not at all easy a matter to achieve. As we have re-

stricted material functions in non-Newtonian fluids, the fluids are assumed

to be incompressible and isothermal. There are only two cases of typically

studied flow configurations (in a sense that they are most widely utilized

as practical rheometric measurements) that are considered in this section.

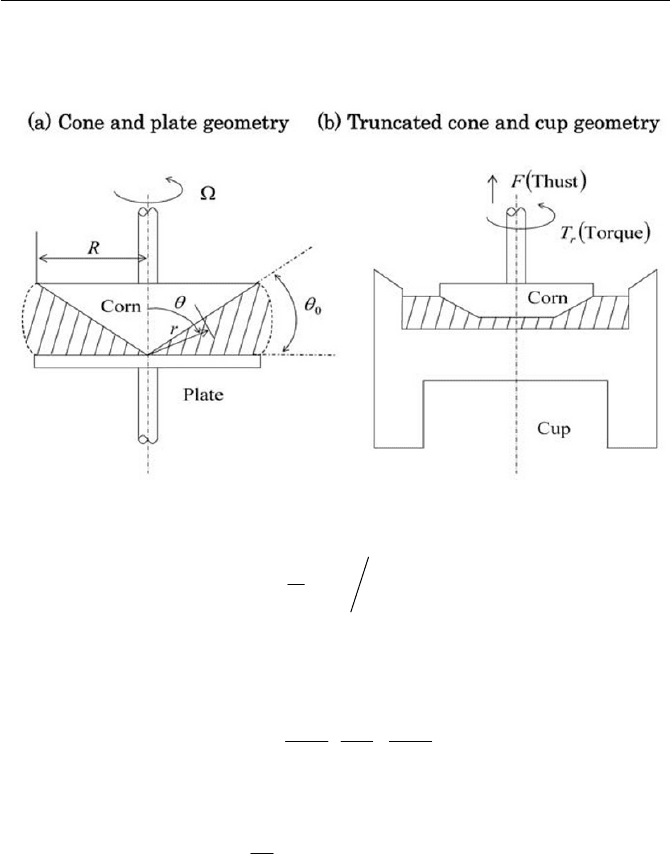
(i) The cone and plate rheometer

That is probably the most popular geometry for rheological measure-

ments of viscoelastic fluids. It is usually used for measuring the shear vis-

cosity and the first normal stress difference simultaneously. Additionally,

the second normal stress difference can be determined from the relation-

ship

2NN  , a value of which is measurable by means of measuring the

pressure distribution across a plate. An ideal cone and plate arrangement is

illustrated in Fig. 7.12(a). A more practical arrangement in an actual

rheometer is also displayed for a reference. In order to recognize the use-

fulness of a practical arrangement in Fig. 7.12(b), it is worth noting that

the reason for utilizing a truncated cone is to avoid frictional torque at the

contact with the plate, and with which it becomes easier to set the correct

gap as required by the geometry of Fig. 7.12(a). The sample fluid is then

placed in the space between the truncated cone and cup.

In order to verify the measuring principle, we shall look the basic ar-

rangement of the cone and plate. As shown in Fig. 7.12(a), a spherical co-

ordinates system



, ,r is used to analyze the flow field, assuming that

the cone is rotated at the angular velocity (either the cone or the plate

can be rotated) at a symmetric axis. Due to the rotational symmetry,

components become identically zero and as the corn angle

is taken to

be very small, i.e. approximately in a range where

3 0 d

, the flow

can be regarded as a narrow gap flow, namely with the condition of the ve-

locity

u of the fluid that can be treated as



u,0,0 u . The velocity

q

428

7.2 Standard Flow and Material Functions

profile

u is also regarded as linear to the position (

) in the gap and is

approximated as

Fig. 7.12 Viscometric (or rheometric) flow

:| ru

(7.2.42)

The shear rate



in a spherical coordinates system is the

-component



with the rate of strain tensor Ȗ



, which is written as

sin෕

෕

sin



(7.2.43)

The substitution of Eq. (7.2.42) for Eq. (7.2.43) yields





(7.2.44)

since here we assume 1sin |

and 0cos |ș . The importance of Eq.

(7.2.44) is that



is independent from the position (

) (free from coor-

dinates) and that



is only determined by the fixed angle

and the rota-

tional speed (angular speed) . It is repeatedly stated that Eq. (7.2.44) is

only true for

if it is very small.

429

7 Non-Newtonian Fluid and Flow

The viscosity

can be obtained from the actual measurement of

torque

T , which is exerted on the shaft of a cone to rotate at a given rota-

tional speed . The net torque on the surface of cone is given where

ITW

sin

෾

෾෾

෾

drr

drdr

dSr

dSTT



ᇫ

(7.2.45)

since 1sin |

and

is independent from coordinates system



,,r

for



. Note that sign to

reflects the shear stress on the solid

surface of a cone. The viscometric function

, the viscosity, will be ob-

tained by substituting Eqs. (7.2.44) and (7.2.45) to Eq. (7.1.1), yielding





(7.2.46)

Therefore, from Eq. (7.2.46), the viscosity is readily determined by meas-

uring

T for a given with fixed geometric constants

and R . The

simplicity of the result given in Eq. (7.2.46) explains why the cone and

plate rheometer is so widely used. In the most of commercially available

rheometers, the range of



is approximately

1010 dd





for pre-

cise measurements, although it is dependent upon a sample fluid.

More importantly, normal stress differences

N and

N can be deter-

mined by a cone and a plate rheometer. Particularly, it is ideal for a cone

and plate geometry to measure the first normal stress difference

N . The

two normal stress differences for

N and

N in a spherical coordinates

system are defined as



TTII

WWJ





(7.2.47)

and







(7.2.48)

430

7.2 Standard Flow and Material Functions

Cauchy’s equation of motion given in Eq. (2.2.6), ignoring the inertial term

DtDu

and the body force term

, can be written as

T ේ0

(7.2.49)

where

T is the total stress tensor defined in Eq. (1.6.13). The

r - and the

r - components of the stress are to be zero. There is no shear force acting

- direction, and the flow is assumed to be symmetrical with respect to

. We can simply write the total stress tensor as follows

rrrr

 ,

TTTT

 pT and

IIII

 pT

(7.2.50)

The Cauchy’s equation, thus, in a spherical coordinates system will be

written in the component form where



T 21

0 

IITT

(7.2.51)

Equation (7.2.51) is further rearranged to give







TTTTII

221

and therefore



TTTT



TTTTII

(7.2.52)

Using the relationship of Eq. (7.2.50) with Eqs. (7.2.47) and (7.2.48), we

can rewrite Eq. (7.2.52) as follows





w

(7.2.53)

Equation (7.2.53) will become a more convenient form for actual meas-

urement when

rrrr

 is eliminated. Rewriting of Eq. (7.2.53) can

be done for





N , being as a unique function of



and independent from

so that



lnlnln w

w

TTTT

(7.2.54)

The value of Eq. (7.2.54) is kept constant since

2NN  is also a

unique function of



, showing that plotting

T against



,ln Rr on a

431

7 Non-Newtonian Fluid and Flow

semi-logarithmic scale should yield a straight line, the slope of which is

2NN  , i.e.

    

 

NNRTrT

ln2

TTTT

(7.2.55)

where Eq. (7.2.55) is obtained by integrating Eq. (7.2.53) from

. However, the measurement for the (total) pressure

TTTT

 pT is

a very difficult task, even when using very small and sensitive flush-

mounted pressure transducers along the plate wall.

On the other hand, the primary normal stress difference

N can be

readily determined by measuring the axial net force (net thrust force)

exerted on a cone (or plate). This is a widely used technique for rheometry.

is generally related to the normal stress

and the atmospheric pres-

sure

p on a cone through the following algebraic manipulation



pRdrdrT

pRdrdrTT

pRdSTT

pRFF

෾෾

෾

sinsincos

sincos

SITTT

STT

TTT





(7.2.56)

since

| , 0cos |

and 1sin |

. Substituting Eq. (7.2.55) for Eq.

(7.2.56) and integrating the equation, we have

 

pRRTRNNR

pRdrrRTdrr

NNF

2ln22

෾෾

SSS







(7.2.57)

We assure that the free surface at

is at the atmospheric pressure

p ,

i.e.



arr

pRT  , so that we can write

N as



















arr

pRT

pRTRTRTN



 

TTTT

(7.2.58)

Combining Eq. (7.2.57) with Eq. (7.2.58) yields the final form

432

7.2 Standard Flow and Material Functions

(7.2.59)

Equation (7.2.59) indicates that

N will be readily determined by

measuring the net axial force (net thrust force)

for a given geometry R ,

subject to the assumption that a small cone angle, a negligible fluid inertial

and edge effect (including surface tension) are involved. For precise meas-

urements, corrections for these possible errors are recommended in Car-

reau, et al. (1997).

Other commonly used rotational rheometers are the parallel plate (or

tensional) rheometer, and the concentric cylinder rheometer (referring to

Section 6.3.1). The common features of these rheometers are based on the

narrow gap flow where the shear rate is to be regarded as being independ-

ent from the spatial coordinates

㧚

(ii) The elongational rheometer

There is an increasing amount of effort for polymer solutions for appli-

cations such as lubrication, turbulent drag reduction, coatings and atomiza-

tion, in which the elongational (or extensional) flow field pre-dominates

the mode of deformation. Continuing interest in polymer melts stems from

the fact that polymer processing operations such as flat film extrusion, film

blowing, fiber spinning and flow molding involve such elongational de-

formation that have been in fact subject of research for many decades. To

characterize the flow of non-Newtonian fluids in the elongational deforma-

tion and to verify their constitutive relations, particularly for those derived

from molecular dynamics, it is necessary to measure the material functions

for shearfree flows. In view of investigating the elongational properties of

polymer solutions, and a higher elongational rate for polymer melts, the

two elongational flow fields, which have been used to try to generate a

uniaxial stretching, are introduced in this section. In order to realize the

flow field, some basic configurations for the types are exemplified via fi-

ber spinning (or extrudate drawing), and pressure driven flows in a con-

are numerous modifications from the basic configurations, and therefore

there is room for further precision measurements, for example, Collyer,

et al. (1988) and Dealy, et al. (1999).

An apparent elongational viscosity

defined in Eq. (7.2.21) for uni-

axial stretching is measured by using the relationship



(7.2.60)

verging channel, as illustrated in Fig. 7.13(a) and (b) respectively. There

433

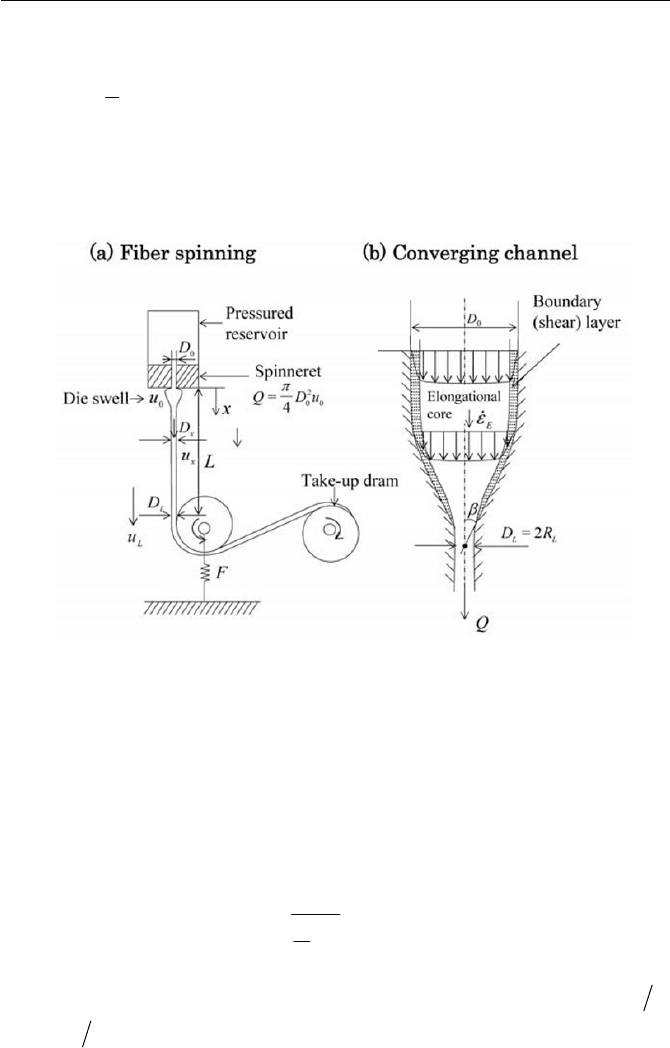
7 Non-Newtonian Fluid and Flow

where

is the net tensile stress, which can be approximated for

xxyy

WWW



, and



is the tensile strain rate. The basic configuration for

measuring

comes from a fiber-spinning apparatus, as illustrated in Fig.

7.13(a), where the test fluid, usually in the state of melt, is forced through

a spinneret by means of a pressurized reservoir. Using a technique with an

Fig. 7.13 Elongational rheometer

The vertical tensile forced

in the filament is then measured on the

rotating dram as indicated in Fig. 7.13(a). There are obviously sources for

error associated with the measurement. They are, for example, the stress

history through the spinneret and the exist point of the capillary channel

(where the die swell occurs), surface tensile, inertia and air friction.

Neglecting these uncertainties and assuming that the force in the filament

is kept constant along its length, the tensile stress would be given where

(7.2.61)

With the continuity of the volume flow rate Q i.e.

uDQ

, where

and

u are the speed of flow at the position 0 x

and

Lx . Equation (7.2.61) is written as

extrudate drawing, the filament (fiber) is cooled by exposure to ambient air,

and is drawn down by means of a take-up dram.

434