Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


Problems
³
»
»
¼
º
«
«
¬
ª
S
TT
E
E
ES
0
2
3
3
sin
11
3
1
1
2 d
n
Re
C
n
n
n
m
/
*
(10)
*
Re is the generalized (rotational) Reynolds number given where
m
rrr
Re
nn
12
2
11
ZU
*
(11)
For reference, the results of Eq. (10) are representatively presented in Fig.
7.5 for a relatively low concentration of a polyacrylamide-water solution
of 2000 ppm with various .
E
As observed in Fig. 7.5, the departure of ex-
perimental data plots from Eq. (10) are speculated to be caused by the ap-
pearance of flow instability, Yamaguchi, et al. (1997).
Problems
7.1-1 For a flow between two concentric rotating cylinders, with reference
to Fig. 6.3(b) in Section 6.3.1, when the outer cylinder is kept sta-
tionary, find the expression for the shear rate
T
JJ
r
, A power law
fluid is assumed in the simple shear flow. Denote
m
and
n
are
power law constants and
r
k is the radius ratio defined by
21
rrk
r
.
Ans.
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
¬
ª
|o
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
r
k
r
k
r
kn
n
r
r
n
1
1
1gapsmallerforand
11
1
2
2
2
2
Z
J
Z
J
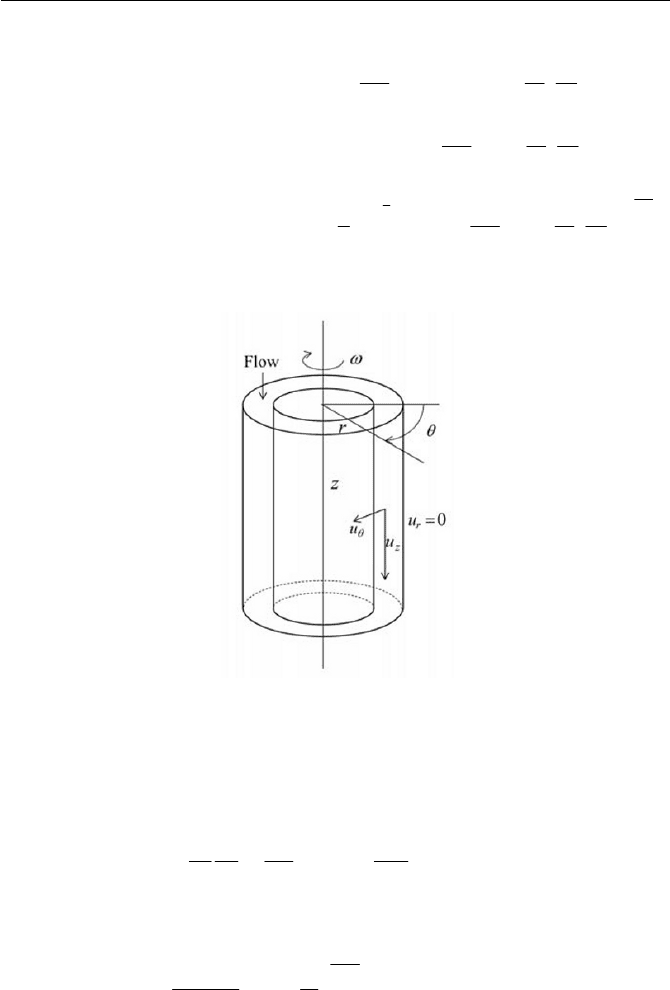
7.1-2 For a helical flow in a cylindrical annular, where the inner cylinder
rotates with the stationary outer cylinder, find the second invariant of
the rate of the deformation tensor, and the shear viscosity
J
K
from
the power law. Note that the helical flow is such as that there is a
flow along the rotational axis with the velocity component of
z
u
with the circumferential velocity component
T
u , whereas the radial
velocity component
r
u is kept zero in the cylindrical annular, as in-
dicated in Fig. 7.6.
415
7 Non-Newtonian Fluid and Flow
Ans.
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
¿
¾
½
¯
®
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
»
»
»
¼
º
«
«
«
¬
ª
¸
¹
·
¨
©
§
»
»
¼
º
«
«
¬
ª
¿
¾
½
¯
®
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
w
w
2
1
2
1
2
1
2
2
22
e
II
2
1
22II
and
n
z
n
e
z
rrz
rr
z
rzrz
r
u
r
r
r
u
mm
r
u
r
r
r
u
r
u
r
r
r
u
T
T
T
T
TT
K
JJ
JJJJ
Fig. 7.6 Helical flow in a cylindrical annular
7.1-3 If the temperature distribution
T
of a steady state laminar flow in a
horizontal pipe is given in the following energy equation
2
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
w
w
r
u
r
T
r
rr
k
zc
JK
Show that
T
in a power law fluid is calculated by
n
n
w
w
R
r
TT
TT
13
0
1
¸
¹
·
¨
©
§
where
0
T and
w
T are the temperatures at the axis ( 0 r ) and at the
416
7.2 Standard Flow and Material Functions
wall ( R
r
) respectively while
c
k is the thermal conductivity of the
fluid. Compare the temperature profile with the velocity profile [Eq.
(11) in Exercise 7.1.2] and provide comments.
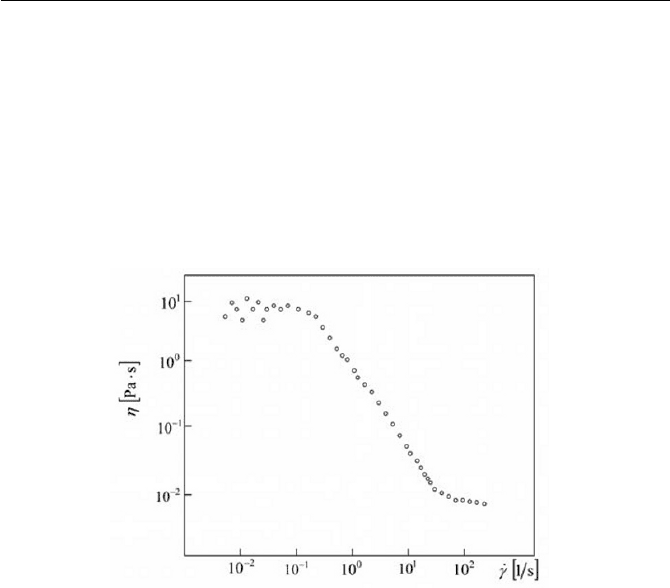
7.1-4 Show the difference between the power law model in Eq. (7.1.4) and
the Carreau-Yasuda model in Eq. (7.1.6) when a set of viscosity-
shear rate data is given as displaced in Fig. 7.7. Determine the con-
stants in both models, when the data in Fig. 7.7 is fitted by both
models.
Fig. 7.7 Sample data of a shear thinning fluid
7.2 Standard Flow and Material Functions
In the previous section, we discovered that the dynamic property of a New-
tonian fluid in an isothermal condition is characterized by a single material
constant, namely the viscosity. However, in non-Newtonian fluids it is
suggested that the material constant depends upon any deformation, time
and/or other conditions yet to be examined. The dynamic properties of the
materials (the interest in this text lies only in substances classifiable as flu-
ids) that are used to determine the material constants in specific non-
Newtonian constitutive equations or simply used to present mechanical
property in engineering problem, are called material functions. The method
of determining the material functions of fluids via experimental means is
called rheometry, in which in classic approach basic rheometric or vis-
cometric flows are introduced to give stress behavior under any given uni-
form deformation. The most common types of flow, used as standard flow
417

7 Non-Newtonian Fluid and Flow
patterns in rheometric work, are the simple shear flow and simple shear-
free flow.
In this section, we shall also look into the most commonly used
rheometries based on the standard flow patterns and find approaches to ob-
tain their material functions.
7.2.1 Simple Shear Flow
A simple shear flow is most typically understood as the plane Couette flow
given in Eq. (6.3.13) as follows
yy
h
U
yu
yxx
JJ
, 0
y
u and 0
z
u
(7.2.1)
The absolute value of
yx
J
, i.e. the shear component of the rate of deforma-
tion tensor, is written as the shear rate
J
in a rheometric flow. In the
rheometry in a steady state measurement, as sketched in Fig. 7.8(a), it is
assumed that
J
is kept constant for such a long time that all associated
stresses generated in a test fluid are time independent in isothermal condi-
tion.
The stress tensor associated with a simple shear flow is given in the
following equation, referring to Eq. (1.6.13)
ji
zz
yyxy
yxxx
IJp
IJpIJ
IJIJp
p ee
ˆˆ
IJIT
»
»
»
¼
º
«
«
«
¬
ª
00
0
0
(7.2.2)
Fig. 7.8 Rheometric (viscometric) flows
418

7.2 Standard Flow and Material Functions
For rheometric flows, the fluid is assumed to be isotropic so that it has no
preferred direction other than the unidirectional flow field. In Eq. (7.2.2),
IJ is sometimes called the deviatoric stress tensor in order to distinguish it
from the total stress tensor T .
Due to the symmetric nature of
T , recognizing the fluid as a non-polar
fluid, the shear stresses
xy
W
and
yx
W
are the same in their value and
yx
W
will be written by using the non-Newtonian viscosity
JK
as previously
defined in Eq. (7.1.1)
ȖȖȘIJ
yx
(7.2.3)
In incompressible fluids, which are subject to study in most non-
Newtonian fluids practice, the pressure
p
in Eq. (7.2.2) cannot be sepa-
rated from normal stress measurements on a solid interface, so that in order
to isolate
p
from the measurements two normal stress differences are only
meaningful when determining the material functions, such that
2
1
1
ȖȖȥIJIJN
yyxx
(7.2.4)
and
2
2
2
ȖȖȥIJIJN
zzyy
(7.2.5)
where the functions
1
\
and
2
\
are called the first and the second normal
stress coefficients respectively. It is noted that
2
J
is used instead of
J
for
the reason that the sign of the two normal stress differences are not to be
changed for the choice of the sign for
J
.
K
,
1
\
and
2
\
are the material functions, which are often referred to
as the viscometric functions. They are directly connected with a design of
unit operations for processing viscoelastic materials and the mechanical
performance of lubricants. The first normal difference
1
ȃ has significant
effects on unique viscoelastic flow phenomena, such as die swell, Weis-
senberg effect and etc. Both
xy
W
and
1
ȃ can be routinely measured by
commercially available instruments. The second normal stress differ-
ence
2
ȃ , however, receives less attention due to difficulties in its meas-
urements, and for the smallness of its value. For many materials,
2
ȃ
would be usually an order of magnitude smaller than, and have the op-
viscometric functions are displayed. The graphs are typical of many
posite sign to, that of
1
ȃ . In Fig. 7.9, the representative data trends of
419
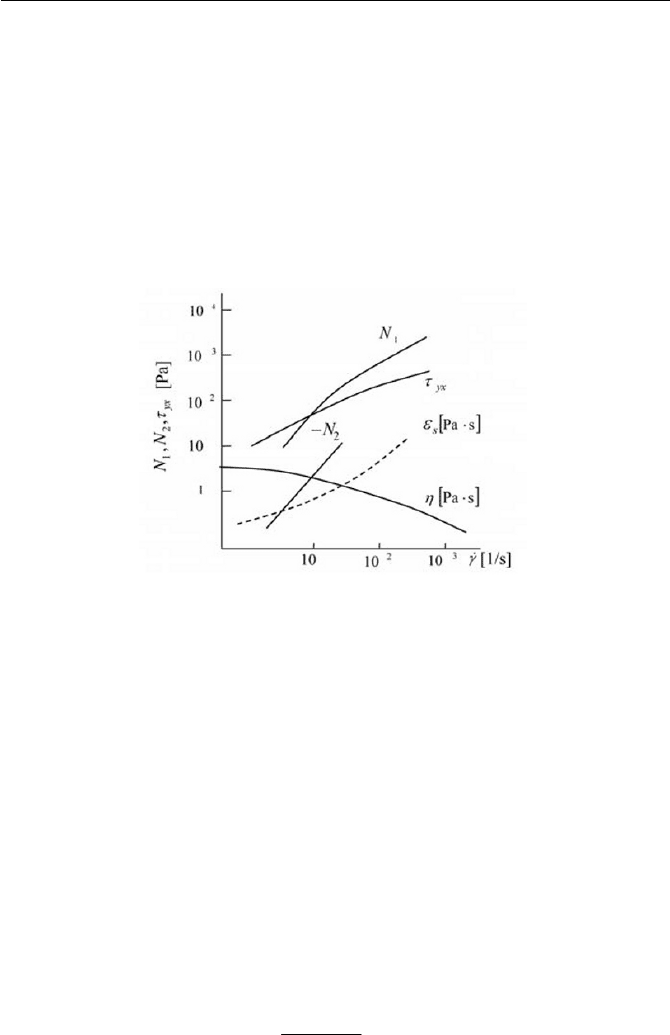
7 Non-Newtonian Fluid and Flow
polymeric liquids (Huilgol and Phan-Thien, 1997). Viscometric functions
are important parameters in order to describe flow characteristics of non-
Newtonian fluids, the determining suitability of the constitutive equation.
It is reassuring that in Newtonian fluids, the total stress tensor for the sim-
ple shear flow is expressed by a tensor form
jixy
yx
p
pIJ
IJp
p ee
ˆˆ
IJIT
»
»
»
¼
º
«
«
«
¬
ª
00
0
0
(7.2.6)
Fig. 7.9 Typically observed viscometric functions (replotted after Huilgol
and Phan-thien, 1997); Polyiso-butylenes in cetane
As it is readily verified in Eq. (7.2.6), the normal stress components in
a deviatoric stress tensor are all zero, i.e. 0
zzyyxx
IJIJIJ . Therefore,
with Newtonian fluids,
Ș is constant for
J
and both
1
ȃ and
2
ȃ are null.
There are many complex and unique flow phenomena that appear in non-
Newtonian fluids due to the fact that there exist normal stresses beside the
non-linearity of the non-Newtonian viscosity.
The appearance of a normal stress in cases of viscoelastic fluids, such
as often seen in polymeric fluids, is particularly important to understand
flow behavior. In such a case, the generations of normal stresses are
closely connected with the elasticity of viscoelastic fluids. A measure of
the elasticity is often quoted by the so-called stress ratio defined as
yx
yyxx
s
IJ
IJIJ
H
(7.2.7)
420
7.2 Standard Flow and Material Functions
In many polymeric fluids,
s
H
is a monotonic increasing function for an in-
creasing
J
, as representatively shown in Fig. 7.9, while in Newtonian flu-
ids
s
H
is always kept at zero.
7.2.2 Shearfree Flow
Shearfree flows are flows in which there is no shear velocity gradient
)( ji
ij
z 0
J
in the rate of the deformation tensor, but only a shearfree
(normal) velocity gradient
ii
J
. There are some variations to achieve an
ideal shearfree flow; they are defined by introducing the elongation rate
H
along one arbitrary axis, such as
H
w
w
xx
x
Ȗ
x
u
(7.2.8)
In dealing with incompressible non-Newtonian fluids, the continuity
equation can be written as
0
w
w
w
w
w
w
z
u
y
u
x
u
z
y
x
(7.2.9)
To satisfy Eq. (7.2.9), the other normal velocity gradients have to be writ-
ten in the following forms, taking into account Eq. (7.2.8) so that
k
y
u
y
w
w
1
2
H
(7.2.10)
and
k
z
u
z
w
w
1
2
H
(7.2.11)
The choice of the axis is arbitrary due to the assumption of isotropic and
frame invariance. The flow fields of shearfree flows defined in Eqs. (7.2.8),
(7.2.10) and (7.2.11) are given by
xu
x
H
(7.2.12)
yku
y
1
2
1
H
(7.2.13)
and
421

7 Non-Newtonian Fluid and Flow
zku
z
1
2
1
H
(
7.2.14)
k is constant and has the range in 10 dd k . In particular, for rheometric
flows, there are some shearfree flows by choice of
H
and k as follows
(i)
0 k
,
0!
H
xu
x
H
,
yu
y
H
2
1
,
zu
z
H
2
1
(7.2.15)
The flow is called an elongational (or extensional) flow, as representa-
tively shown in Fig. 7.8(b). The flow uniaxially stretches in
x
-direction,
while contracting toward the center from the
y and
z
axis points.
(ii)
0 k
,
0
H
xu
x
H
,
yu
y
H
2
1
,
zu
z
H
2
1
(7.2.16)
The flow is called a biaxial stretching flow. This is opposite to (i),
where in
y and
z
, a directional stretching flow persists, while along the
x
direction the flow is contracting.
(iii)
1 k
xu
x
H
, yİu
y
,
0
z
u
(7.2.17)
The flow is called a planar elongational flow. The flow appears along
both the
x
and y plane, where in
x
direction flow stretches and in y direc-
tion flow contracts, and vice versa, depending upon the choice of the sign
of
H
.
Similar to a steady shear flow,
H
is kept constant for such a long time
that all associated stresses generated in test fluids are time independent at
isothermal conditions. The stress tensor associated with shearfree flows are
given via the following equation
ji
zz
yy
xx
p
p
p
p
ee
ˆˆ
IJIT
¸
¸
¸
¹
·
¨
¨
¨
©
§
W
W
W
00
00
00
(7.2.18)
Along with the thought of a simple shear flow, two normal stress dif-
ferences are only meaningful when determining the material functions for
a shearfree flow, i.e.
422

7.2 Standard Flow and Material Functions
H
H
,kȘIJIJ
yyxx 1
(7.2.19)
and
H
H
,kȘIJIJ
zzyy 2
(7.2.20)
where
1
K
and
2
K
are the viscometric functions for shearfree flows of iso-
tropic fluids. Particularly in view of rheometry, the case of
0 k is impor-
tant, so that Eqs. (7.2.19) and (7.2.20) become
H
H
yyxx
e
IJIJ
ȘȘ
0
1
,
(7.2.21)
and
00
2
,
H
K
(7.2.22)
e
K
is called the elongational viscosity (or extensional viscosity) and also
called the Trouton viscosity. It is readily obtain through the elongational
viscosity
e
K
of the fluid, i.e.
0
3
KK
e
, a result found via Trouton (1906).
The rheometric measurement of an elongational viscosity is not easy, as is
the shear viscosity in general, due to the difficulties of the isolation of
shear influences. A typical measurement for data is displayed in Fig. 7.10,
for a polystyrene melt (replotted after Munstedt 1993). In many polymeric
fluids, the elongational viscosity is typically much larger (at least three
times larger than a zero-shear viscosity) than its viscometric counterpart. It
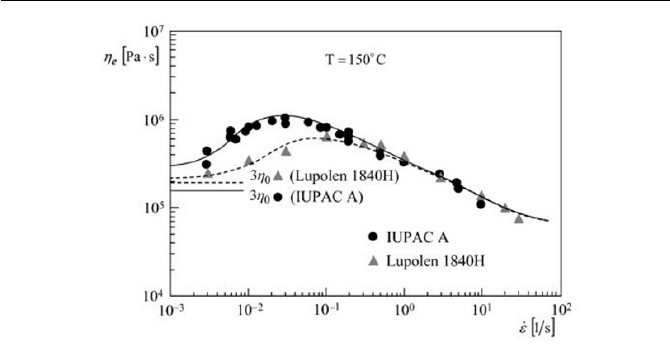
is noted that in Fig. 7.10,
0
K
J
K
o
as 0o
J
,
0
K
is the zero-shear vis-
cosity.
As observed in Fig. 7.10, the elongational viscosity
e
K
approaches to
the value of
0
3
K
as 0o
J
, where (at very low shear rate region) the shear
stress is almost proportional to
J
, showing Newtonian fluid characteristics
and the region called the first Newtonian region (also see Fig.7.1(b)).
Some rheometric measurements on elongational viscosity are found in ref-
erence to Tirtaatmadja et al. (1993).
There are some elongational flow fields typically encountered in engi-
neering practice. They are, for example, converging and diverging chan-
nels, squeezing film, spinning synthetic fibers from molten liquid and so
forth. The tubeless-siphon, in which a siphon continues to ascend even
though the upstream end has been withdrawn from the fluid surface, is also
prominently dominated by the elongational flow field. And, moreover flow
behavior in viscoelastic fluids is widely discussed from the view point of
elongational viscosity in recent years.
423
7 Non-Newtonian Fluid and Flow
Fig. 7.10 Elongational viscosity (replotted after Munstedt 1993)
7.2.3 Oscillatory Rheometric Flow
Viscometric functions
K
,
1
\
,
2
\
and
e
K
, derived from standard flow pat-
terns, which, in view of rheometric work, are commonly the simple shear
and shearfree flows, are defined as time independent variable functions.
However, in dealing with viscoelastic fluids, the dynamic properties and
time dependent material functions, are of considerable practical impor-
tance, as flow behavior can often be directly related to the viscous, as well
as elastic parameters, where the fluids undergo the transient process. In
view of processing such material, the dynamic properties can also yield
strong insight into the microstructure of the material. Among other time
dependent material functions, the most widely used rheometric flow to de-
termine the linear viscoelastic properties of polymeric fluids is a small am-
plitude oscillatory shear flow. The idealistic flow configuration is that the
upper plate of Fig. 7.8(a), i.e. the simple shear flow, is oscillated with a
small amplitude to give the shear strain
J
as a function of time in such a
way that
tt
Z
J
J
sin
0
(7.2.23)
where
0
J
is the shear strain amplitude and
Z
is the frequency. The shear
strain rate
J
is then obtained by differentiating Eq. (7.2.23) to give
tt
Z
J
Z
Z
J
J
coscos
00
(7.2.24)
where
0
J
is the shear rate amplitude.
424
