Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

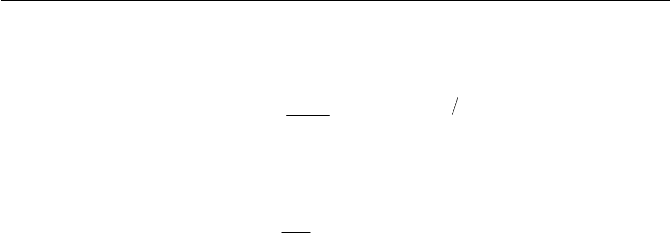
7.3 Viscoelastic Fluid and Flow
Equation (7.3.71) can be reduced to a number of constitutive equations,
as is often referred in the literature. For example, by setting
¦
c
c
odd
tt
ettM
D
ODS
O
K
22
2
0
96
(7.3.81)
and
³
nnn
ˆˆˆ
C
dW :ln
4
5
ൖ,ൕ
1
S
(7.3.82)
we can obtain the Curtiss–Bird (1981) constitutive equation.
7.3.3 Viscoelastic Models to Standard Flow and Application to
Some Engineering Flow Problems
In the preceding section we shall see the rheological predictions of some
simple viscoelastic constitutive equations. However, it should be kept in
mind that these viscoelastic constitutive equations would be used to por-
tray the rheological properties that are observed in typical polymeric fluids.
There are, in fact, a wide variety of material functions, as overviewed in
Section 7.2. The cases examined here are chiefly based on the properties,
in view of applying the equations to engineering problems, that are de-
pendent upon the shear viscosity
JK
and the first normal stress coeffi-
cient
J\
1
in steady, simple shear flows, and also the elongational viscos-
ity
HK
e
at finite level of the elongational rate
H
in particular.
Some of typical flow problems are exemplified in the later section to
illustrate the methods of applying the equations.
7.3.3.1 UCM, CRM and Giesekus Equations
In order to examine rheological characteristics of the constitutive equations
at a steady state, an assumption is made to state that a time period after
imposing a steady shear or elongation is much longer than the relaxation
time constant, which is a property of fluid at rest.
We shall begin to examine the UCM equation given in Eq. (7.3.47), for
simple shear and shearfree flows. Firstly, in the simple shear flow, UCM
equation is written (with reference to Exercise 7.3.1) where
465

7 Non-Newtonian Fluid and Flow
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
000
001
010
000
00
02
00
0
0
0
JKW
WW
JO
W
WW
WW
yy
yyxy
zz
yyxy
xyxx
(7.3.83)
Thus, from Eq. (7.3.83) we are able to obtain the material functions as
JKW
0
xy
,
2
01
2
JOKWW
yyxx
N and 0
2
zzyy
N
WW
(7.3.84)
which gives us
0
K
J
W
K
xy
,
0
2
1
1
2
OK
J
\
N
and 0
2
2
2
J
\
N
(7.3.85)
Secondly, in shearfree flows, the UCM equation is similarly written as its
component form
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
k
k
k
k
zz
yy
xx
zz
yy
xx
100
010
002
1
2
1
00
01
2
1
0
00
2
00
00
00
0
HK
W
W
W
HO
W
W
W
(7.3.86)
Thus, from Eq. (7.3.86) in the case of uniaxial stretching, i.e
0
k , in an
elongational flow, the elongational viscosity
e
K
is obtained where
HOHO
K
H
W
W
K
121
3
0
yyxx
e
(7.3.87)
In a similar manner, the CRM equation given in Eq. (7.3.51), in a sim-
ple shear flow, can be written as its component form
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
000
0
2
0
2
00
0
0
xy
yyxx
yyxx
xy
zz
yyxy
xyxx
W
WW
WW
W
JO
W
WW
WW
466
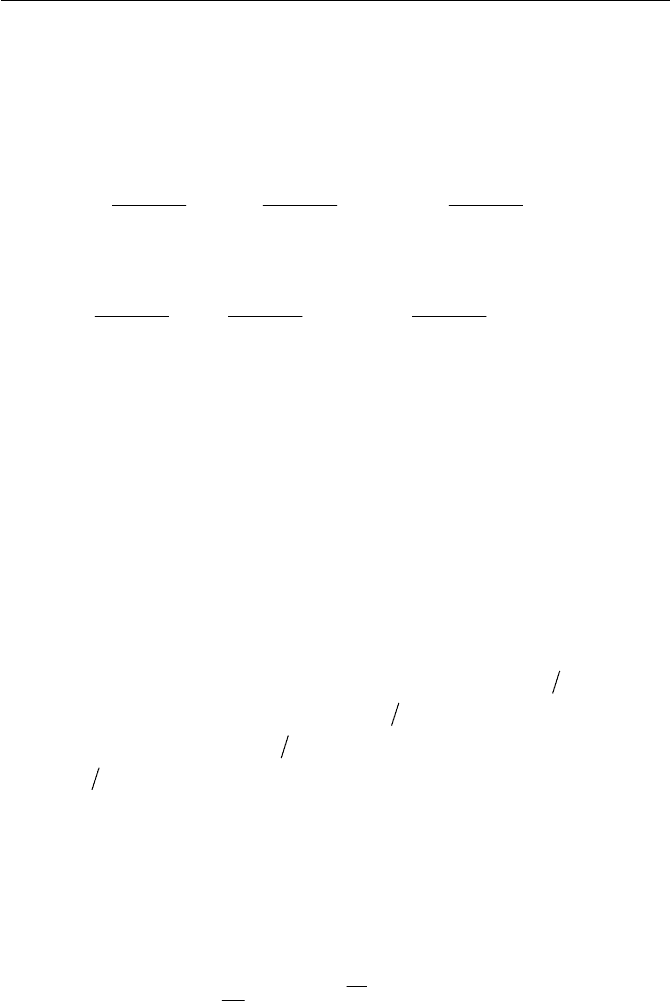
7.3 Viscoelastic Fluid and Flow
¸
¸
¸
¹
·
¨
¨
¨
©
§
000
001
010
0
JK
(7.3.88)
Thus, from Eq. (7.3.88), the material functions are
J
JO
K
W
2
0
1
xy
,
2
2
0
1
1
2
JO
JOK
N and
2
2
0
2
1
JO
JOK
N
(7.3.89)
which gives us
2
0
1
JO
K
K
,
2
0
1
1
2
JO
O
K
\
and
2
0
2
1
JO
O
K
\
(7.3.90)
If we proceed along the same line of reasoning, for the shearfree flow, the
CRM equation is written as
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
k
k
zz
yy
xx
100
010
002
00
00
00
0
HKO
W
W
W
0
(7.3.91)
which readily gives the elongational viscosity in its simplest form for
0 k as follows
0
3
KK
e
(7.3.92)
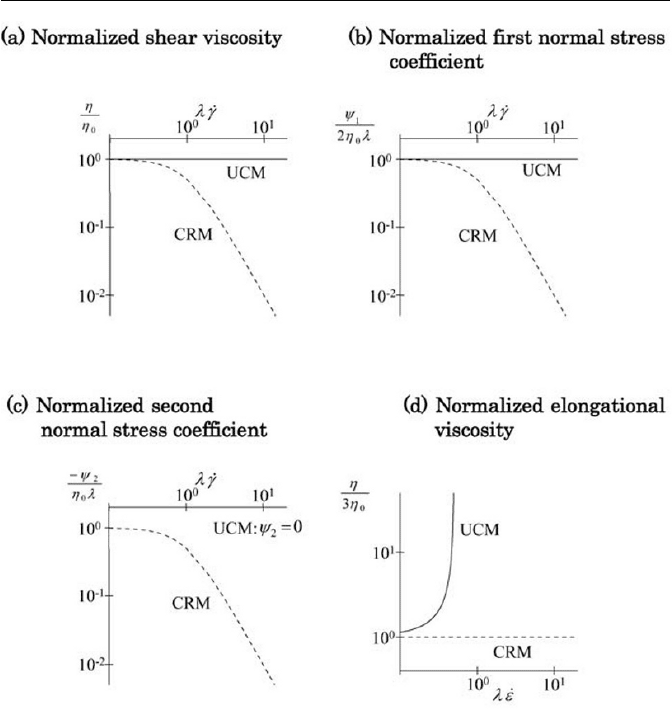
Figure 7.20 shows a qualitative comparison of rheological predictions
of UCM and CRM equations for: (a) normalized viscosities
0
K
K
, (b) nor-
malized first normal stress coefficients
O
K
\
01
2 , (c) normalized second
normal stress coefficients
OK\
02
, and (d) normalized elongational vis-
cosities
0
3
KK
. The CRM equation gives fairly good qualitative predic-
tions on shear thinning characters. However, with the CRM equation, the
elongational viscosity becomes constant for all
H
, giving a Trouton value
of
0
3
KK
, which is not realistic with general polymeric fluids, which of-
ten show the strain hardening.
It is useful to mention that the shear viscosity given in Eq. (7.3.90) can
be modified to write:
>@
2
1
2
0
1
n
Ȗ
O
K
K
(7.3.93)
–
467
7 Non-Newtonian Fluid and Flow
Fig. 7.20 Rheological predictions via UCM and CRM equations
Namely, Eq. (7.3.93) is the equivalent form with the Carreau-Yasuda for-
mula presented in Eq. (7.1.6) where
2
a
and 0
f
K
. Usually, the shear
dependent material functions given in Eq. (7.3.93) give too large predic-
tion to agree with most data on polymeric fluids, for which the range of
n
is
0150 .. dd n
The Giesekus equation given in Eq. (7.3.59) is a nonlinear constitutive
equation, which contains the quadratic term of
IJ with a given constant of
the mobility factor
D
. Choosing
D
gives more realistic predictions in both
melts and solutions of polymeric fluids. Now, cases are examined for the
468
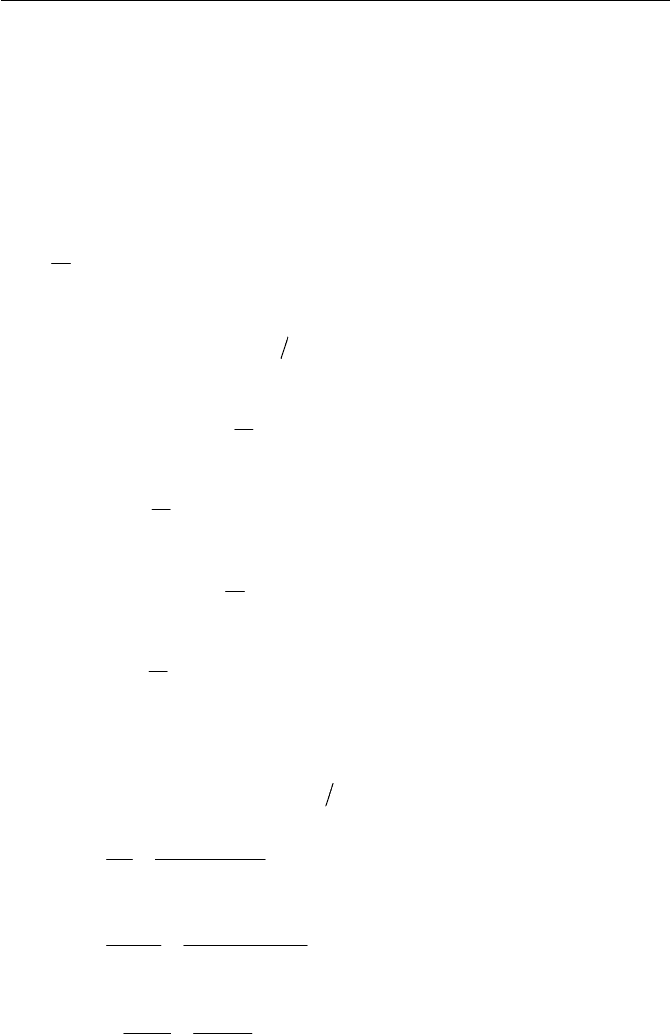
7.3 Viscoelastic Fluid and Flow
equation in steady simple shear flow:
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
000
00
02
00
0
0
1 yy
yyxy
zz
yyxy
xyxx
W
WW
JO
W
WW
WW
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
000
001
010
00
0
0
2
22
22
JK
W
WWWWWW
WWWWWW
D
P
zz
yyxyyyxyxyxx
yyxyxyxxxyxx
G
(7.3.94)
where
G is defined by
1
OK
P
G . Equation (7.3.94) has, thus, algebraic
relationships for four stress components as follows
02
22
1
xyxxxyxx
G
WW
D
WJOW
(7.3.95)
0
22
yyxyyy
G
WW
D
W
(7.3.96)
0
1
JKWWWW
D
WJOW
P
yyxyxyxxyyxy
G
(7.3.97)
0
2
zzzz
G
W
D
W
(7.3.98)
Solving Eqs. (7.3.95) to (7.3.98) for each stress component
xx
W
,
yy
W
,
xy
W
and
zz
W
, we can obtain a steady state of normalized material functions for
the simple shear flow, where
J
W
K
xy
and
]D
]
K
K
211
1
2
P
(7.3.99)
2
1
1
1
1
1
2
JO]D
D]]
OK
\
P
(7.3.100)
2
1
1
2
JO
]
OK
\
P
(7.3.101)
469

7 Non-Newtonian Fluid and Flow
]
is a parameter defined by
[D
[
]
211
1
(7.3.102)
and for
[
^`
2
1
2
1
2
1
2
18
11161
JODD
JODD
[
(7.3.103)
The elongational viscosity predicted from the Giesekus equation may
be obtained for the steady shearfree flow of uniaxial stretching, i.e.
0 k ,
as follows
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
100
010
002
00
00
00
00
00
002
00
00
00
2
2
2
1
HK
W
W
W
D
W
W
W
HO
W
W
W
P
zz
yy
xx
zz
yy
xx
zz
yy
xx
G
(7.3.104)
Equation (7.3.104) contains three stress components, for which the alge-
braic equations can be written where
022
2
1
HKW
D
WHOW
Pxxxxxx
G
(7.3.105)
0
2
1
HKW
D
WHOW
Pyyyyyy
G
(7.3.106)
0
2
1
HKW
D
WHOW
Pzzzzzz
G
(7.3.107)
Solving Eqs. (7.3.105) to (7.3.107) yields the normalized elongational
viscosity to write
470
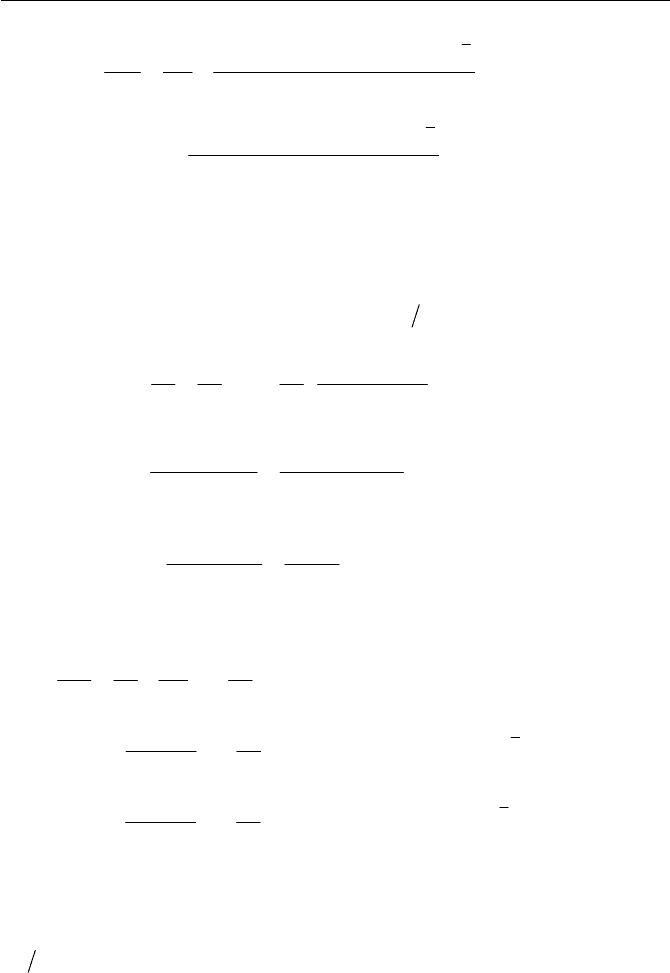
7.3 Viscoelastic Fluid and Flow
^`
^`
HOD
HOHOD
HOD
HOHOD
DK
K
1
2
1
2
11
1
2
1
2
11
6
2121
6
42141
2
1
3
P
e
(7.3.108)
In the application of polymeric solutions, the Giesekus equation can be
written in the form given in Eq. (7.3.63), where the parametric relationship
is given in Eq. (7.3.64). Using the notation found in Eq. (7.3.64), the
steady state normalized material functions are calculated to give, for the
simple shear flow by letting
J
W
K
K
K
xyps
0
]D
]
O
O
O
O
K
K
211
1
1
2
1
2
1
2
0
¸
¸
¹
·
¨
¨
©
§
(7.3.109)
2
1
210
1
1
1
2
JO]D
D]]
OOK
\
(7.3.110)
2
1
210
2
JO
]
OOK
\
(7.3.111)
and for the shearfree flow of uniaxial stretching:
^`
^`
2
1
2
11
1
2
1
2
1
2
11
1
2
1
1
2
1
2
0
21211
6
1
421411
6
1
1
2
1
3
HOHOD
O
O
HOD
HOHOD
O
O
HOD
O
O
DO
O
K
K
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
e
(7.3.112)
In Fig. 7.21, similar to the cases of the UCM and CRM equations in
Fig. 7.20, the rheological predictions via the Giesekus equation for solu-
tions are also plotted qualitatively from Eqs. (7.3.109) to (7.3.112) for
0010
12
.
OO
(i.e. for a relatively small retardation time). The choice of
the mobility factor
D
would soften the material functions with an idea that
0
D
gives the limit of the UCM equation. The Giesekus model often
471
7 Non-Newtonian Fluid and Flow
gives a good rheological estimate for melts and solutions in practical use,
which also reflects the popular quotation found in the CFD.
Fig. 7.21 Rheological predictions via the Giesekus equation for exam-
ple;
0010
12
.
O
O
7.3.3.2 Unidirectional Basic Flow Problems
There are many interesting and rather unexplained flow phenomena that
occur in a flow of viscoelastic fluids. In engineering flow situations they
are extremely complicated due to viscous and elastic effects interacting in
the flow field where, in most cases, the only way to examine the flows is to
obtain the numerical solutions. One particular problem arises, however,
when a realistic constitutive equation is used to simulate viscoelastic flows,
while the convergence of numerical solutions is often difficult due to the
nonlinearity of the constitutive equation and the boundary conditions,
whether if they are no-slip or slip conditions at a given wall.
472
7.3 Viscoelastic Fluid and Flow
In this section of the chapter, we will try to interpret some of viscoelas-
tic flows using simple linearlized theories. This certainly limits the type of
results we can obtain, bearing in mind.
As a representative case, the transient Poiseuille flow of a viscoelastic
fluid may be treated numerically using a simple finite difference technique.
Note that the configuration has already been treated in Section 6.4.3 in the
Newtonian case.
Denote the unidirectional flow field in a cylindrical coordinates system
when
truu
z
,
, and the shear stress
tr
rz
,
WW
. The equation of motion,
the Cauchy’s equation of motion, for the cylindrical flow problem, is writ-
ten as
r
r
r
tP
t
u
w
w
w
w
W
U
1
(7.3.113)
where
zptP ww .We assume a linear viscoelastic fluid represented by
the Maxwell model from Eq. (7.3.39), setting
xy
WW
as follows
r
u
t w
w
w
w
0
K
W
OW
(7.3.114)
Following the nondimensional parameters defined in Eq. (6.4.56) repeat-
edly, they are
0
r
r
r
*
,
t
rr
t
t
2
0
2
0
0
XUK
*
and
Pr
u
u
2
0
0
4
K
*
(7.3.115)
also, defining a nondimensional stress and relaxation time as
WW
Pr
0
4
*
and
2
0
r
XO
]
(7.3.116)
Therefore, for a set of flow field and constitutive equations, Eqs.
(7.3.113) and (7.3.114) are written respectively by
*
*
*
*
*
*
rrt
u
WW
w
w
w
w
4
(7.3.117)
and
*
*
*
*
*
r
u
t w
w
w
w
W
]W
(7.3.118)
These equations are to be solved with the boundary and initial conditions
of the problem. They are respectively
473

7 Non-Newtonian Fluid and Flow
0
0
w
w
*
**
),(
r
tu
and
01 ),(
**
tu
(7.3.119)
and
00
),(
**
ru and 00 ),(
**
r
W
(7.3.120)
Equation (7.3.120) represents the start-up flow from a rest with no-slip at
wall and Eq. (7.3.119) represents the symmetric condition at the center of
pipe. We will impose one more condition on the pressure that follows step
change in pressure gradient imposed upon the fluid at rest, i.e.
0 )(
*
tP for 0ddf
*
t
(7.3.121)
and
Constant
)(
*
tP for fdd
*
t0
(7.3.122)
From a view of CFD, we shall here take an approach to obtain numeri-
cal solutions, by using a finite difference technique. The most direct means
of discretisation is provided by replacing the derivatives of Eqs. (7.3.117)
and (7.3.118) by equivalent finite difference expressions. The algebraic
equations produced by the discretisation with 2nd order central difference
in space and 1st order forward difference in time (the so-called Euler
method) would be
i
kikiki
ki
ki
rrt
uu
,,,
,
,
WWW
2
4
111
(7.3.123)
and
r
uu
t
kiki
k
iki
ki
WW
]W
2
1111
1
,,,,
,
(7.3.124)
which gives explicit finite difference formulation
¸
¹
·
¨
©
§
i
kikiki
ki
ki
rr
tuu
,,,
,
,
WWW
2
4
11
1
(7.3.125)
and
kikikiki
uu
tr
t
t
,,
,,
1111
2
]
W
]
]
W
(7.3.126)
where
rir
i
' for i =0, 1, 2 m and tkt
k
for k =0, 1, 2, 3 f .
''
''
'
'
'
'''
'
. . . . . .
474
