Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

6 Newtonian Flow

by knowing the pressure distribution in the inviscid core flow given in Eq.

(6.5.11) over the same surface shape.

It should be mentioned that the boundary layer equations are valid for

moderately curved surfaces, and for that

(6.5.12)

where

is a representative curvature of the curved surface.

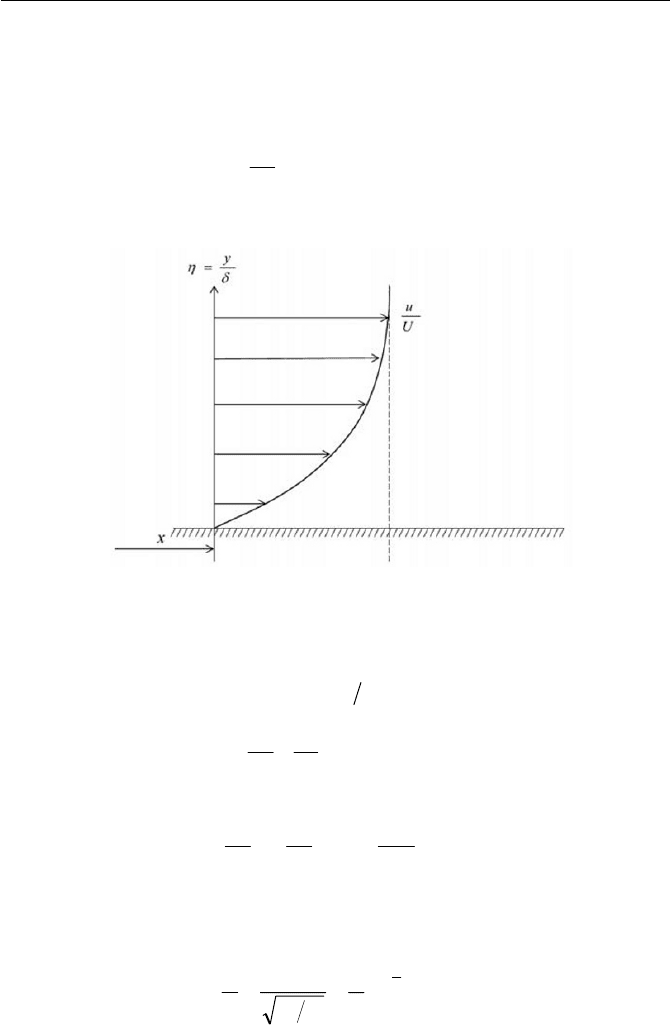
Fig. 6.19 Nondimensional velocity profile by

Blasius gave analytical solutions to the boundary layer equations, as-

suming that the flow is steady and the pressure distribution in an inviscid

flow over a flat plate is uniform, i.e.

w xp , so that we have



(6.5.13)



(6.5.14)

Blasius showed that a similarity solution (the velocity profile) of these

equations can be obtained by introducing a new parameter

(6.5.15)

344

6.5 Laminar Boundary Layer Theory

where

is adopted from Eq. (6.5.7). Note that

is a conventionally de-

fined parameter (it should not be confused with the viscosity), which

scales the directional distance from the wall at position

, as shown in Fig.

6.19. It is reasonable to state that the nondimensional velocity distribution

function

f would be expressed in terms of

to write



(6.5.16)

Since the velocity profile would be written in terms of

, we may be able

to introduce a stream function

by letting

 

KKK

fdf

, as follows

 

KX\

fUxyx ,

(6.5.17)

Using Eq. (6.5.17), we are able to write the velocity component u and v

where



(6.5.18)

 ^`

KKK

v 



(6.5.19)

and a substitution of Eqs. (6.5.18) and (6.5.19) to Eq. (6.5.14) yields



ccc

fff

(6.5.20)

f for 0

(6.5.21)

and

(6.5.22)

It is mentioned that the function



that satisfies Eq. (6.5.20) and the

boundary condition is the Blasius solution.

The exact analytic solution has not yet been obtained. Otherwise,

matching inner and outer series solutions is found to be one of techniques

for solving the equation such as shown by Meksyn (1961) and Rosenhead

Equation (6.5.20) is the Blasius equation, which is a nonlinear, third-order,

ordinary differential equation that is solved for the boundary conditions

345

6 Newtonian Flow

(1963) that gives:

(i) Near wall;







!232

(6.5.23)

where 1

C , 1

C , 11

C , 375

C , 27897

C and 3817137

C .

(ii) Infinite distance from wall;



³³





KKJEKK

dedf

(6.5.24)

(iii) Matching

and

;

Matching Eqs. (6.5.23) and (6.5.24) is given by taking the constants

3320

731

and 2310.

where f , f

and f

are joined in the region of the solution.

The numerical solution for the Blasius equation is readily available. Note

that at the edge of the boundary layer, which is defined as the location

where 99.0 Uuu

, occurs for 0.5914 | .

, the result of a numeri-

cal solution for the Blasius equation. Therefore, we have a value of 99%

boundary layer thickness given as

0.5



xRe

(6.5.25)

It is confirmed that the Blasius solution does agree with experiments, such

as Liepmann’s (1943), showing that the similarity of the velocity profile in

the flat plate is held.

Note that from experimental verification, the turbulent boundary layer

starts to persist for a flat plate with a zero attack angle for

105ut

Re .

6.5.2 Integral Analysis of Boundary Layer Equation

The direct analytical approach to solve the boundary layer equation in-

volves much difficulties, as seen from the solution of the Blasius equation.

However, if the velocity profile within the boundary layer can be assumed

to be known, we may be able to gain a great deal of quantitative informa-

346

6.5 Laminar Boundary Layer Theory

tion by simply integrating Prandtl’s boundary layer equation. Particularly,

in most of engineering problems, estimation of a frictional drag force over

an objective solid wall is of primary importance.

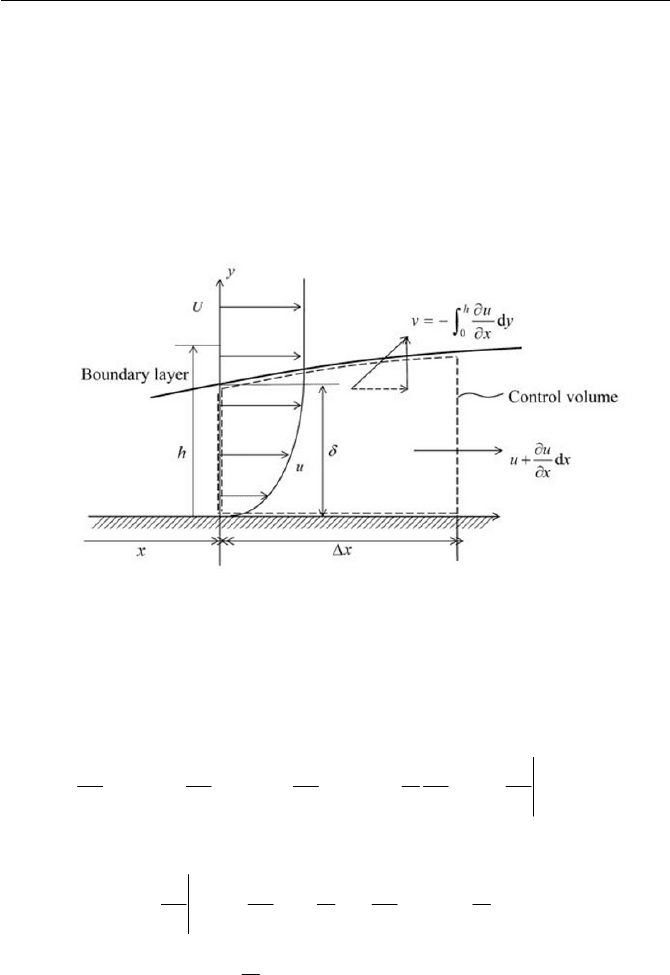
In this section, we will derive the momentum integral equation, follow-

ing an idea first put forth by von Kàrmàn (1921), and calculate the fric-

tional drag on a flat plate at high Reynolds numbers. The control volume

chosen for the analysis is sketched in Fig. 6.20, where the velocity is de-

fined at a downstream position

from the leading edge of a flat plate.

Fig. 6.20 Control volume for a boundary layer

Consider the boundary layer equation, the momentum equation in

di-

rection given in Eq. (6.5.9), and integrate the equation from the wall to the

height beyond the thickness of the boundary layer, i.e. hy dd0, as fol-

lows

hhhh

vdy

udy

0000







³³³³

(6.5.26)

The last term on the right hand side of Eq. (6.5.26) can be written as



(6.5.27)

when

is the wall of shear stress. The last term of Eq. (6.5.26) can be

written as

347

6 Newtonian Flow



(6.5.28)

It should be kept in mind that Eq. (6.5.27) or (6.5.28) can be valid for any

flow mode (laminar or turbulence). Similarly, the continuity equation in Eq.

(6.5.8) is integrated to give



(6.5.29)

Using Eq. (6.5.29), the last term on the left hand side of Eq. (6.5.26) can

be reduced to the following form, after eliminating

v and carrying out the

integration by parts

³³³



hhh

dydy

000

³³





udy

(6.5.30)

The momentum equation is thus written altogether as

hhhh

Udy

udy





³³³³

0000

(6.5.31)

The pressure term in Eq. (6.5.31) is eliminated by the inviscid flow equa-

tion in Eq. (6.5.11), and after some arrangements, we can write the equa-

tion to give

hhh

hhhh

udy

Udy

udy

Udy











³³³

³³³³

000

0000

(6.5.32)

The resultant integral equation of momentum change seems formidable

at first glance, but leads to no novel algebraic difficulties by reducing the

common terms together as follows

 



hhh

dyuU

dyuUu

dyuU





³³³

000

(6.5.33)

Some simplifications are expressed in Eq. (6.5.33) by virtue of defin-

ing the properties of

and

by taking foh , where for the fixed con-

trol volume the integral equation of Eq. (6.5.33) is rewritten with the fol-

lowing compact form

348

6.5 Laminar Boundary Layer Theory





(6.5.34)

where we define

and

respectively



1dy

(6.5.35)



1dy

(6.5.36)

Equation (6.5.34) was first derived by von Kàrmàn (1921) and is often re-

ferred to as the Kàrmàn integral equation. The equation is valid for both

laminar and turbulence flows, as long as the velocity profile





tyxu ,, is

known a priori. The boundary conditions for the integration in Eq. (6.5.34)

are

0 u for 0 y

and 0

for f y

(6.5.37)

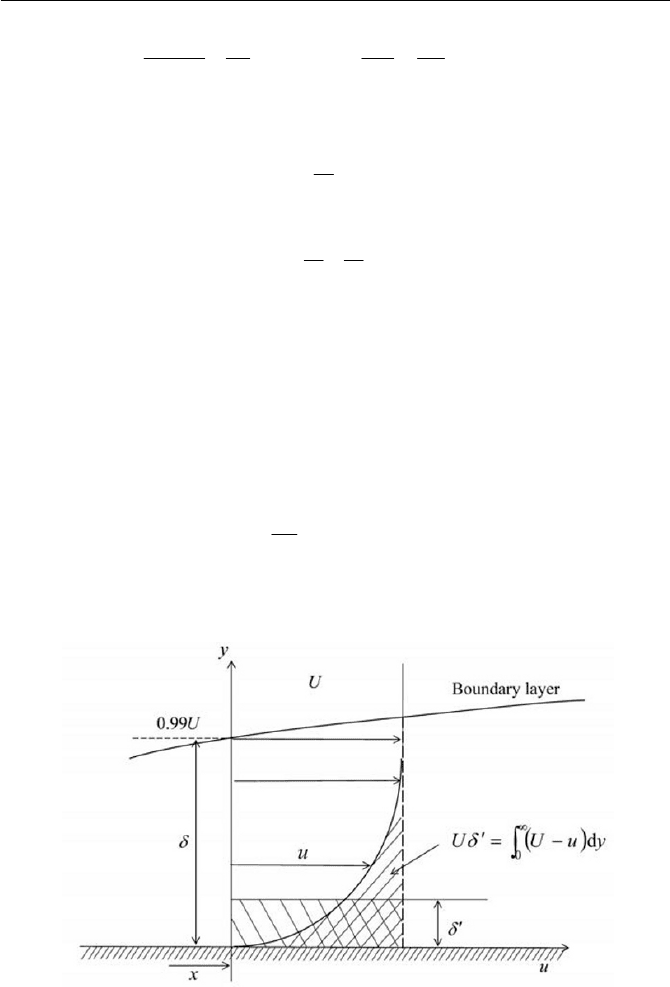
Fig. 6.21 Displacement thickness

349

6 Newtonian Flow

As seen in Eq. (6.5.34), there are two new additional lengths in boundary

layer theory, as defined in Eqs. (6.5.35) and (6.5.36). There are the dis-

placement thickness

and the momentum thickness

. The displacement

thickness is the equivalent thickness of the deficit of volume flow rate in

the boundary layer compared to the inviscid flow limit by the continuity

consideration, as schematically shown in Fig. 6.21. The momentum thick-

ness is the equivalent thickness of the momentums loss due to the deficit of

mass (volume flow rate) in the boundary layer.

For a steady flow over a flat plate with a zero pressure gradient, that is

0 ww xp

/ and



const. UxU , i.e.

0 ww xU /

, the momentum loss is

solely due to wall friction, and this is simply expressed in Eq. (6.5.34) as

(6.5.38)

The momentum thickness

is often used to represent a characteristic

length in turbulent boundary layer studies.

6.5.3 Boundary Layer Separation

The boundary layer theory based on thin layer approximations discussed in

this chapter does not apply in so-called separated regions, such as observed

along curved surfaces. Nevertheless, the boundary layer theory can give an

estimate to the point of occurrence of the separation, and is able to give an

explanation of the phenomena. Here we will consider the phenomenon of

boundary layer separation and vortex formation behind bluff bodies.

The velocity profile in the boundary layer depends upon the potential

flow outside the boundary layer. The core flow, which may be accelerated

or decelerated, is determined by the flow situation and geometry of the

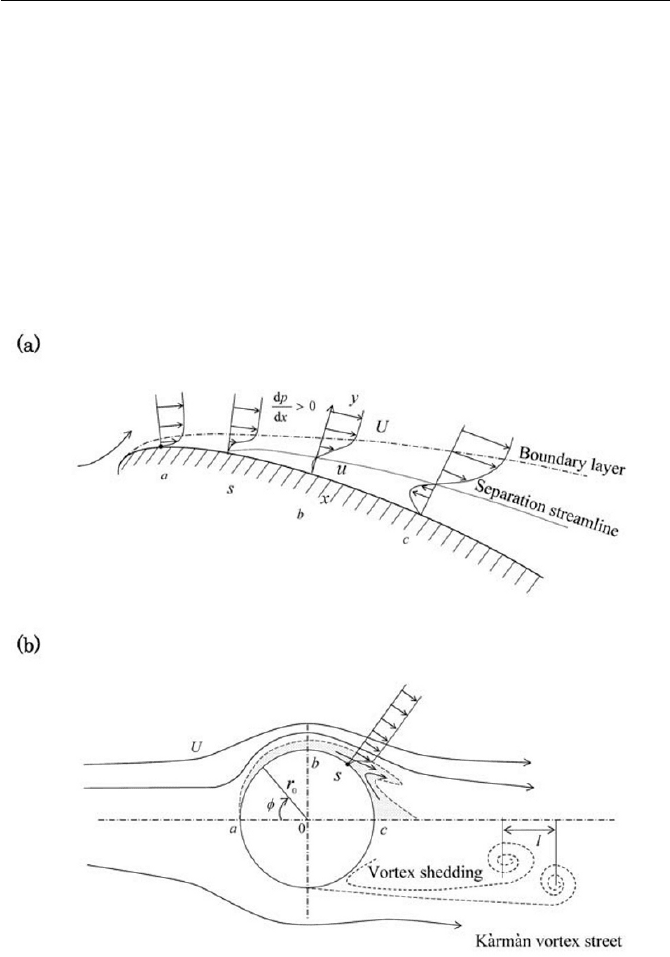
wall. The phenomenon of boundary layer separation occurs for flow, which

has an adverse pressure gradient, 0!dxdp

/ , as illustrated in Fig. 6.22(a).

Particularly with a flow over a curved surface, such as flow over an airfoil,

as representatively displayed in Fig. 6.22(a), the inviscid flow is deceler-

ated, the separation of boundary layer from the wall starts at s and in the

downstream b and

c , the reverse flow persists with 0ww yu / , whereas

in the upstream

the flow is forward at

direction with 0!ww yu / . The

separation streamline, which is of a zero velocity contour coincides with

the wall, leaves the surface at the separation point s and extends toward the

downstream. When the Reynolds number of flow is sufficiently high, at

the downstream of the separation point below the separation streamline,

the wake takes place which is typically characterized by irregular eddies.

350

6.5 Laminar Boundary Layer Theory

In the wake, large energy loss due to high mixing may occur, resulting in a

large pressure loss, and causes a higher pressure difference between the

leading edge and the trailing edge, increasing in the pressure drag. The

boundary layer separation may be seen in a diffuser or in a highly diver-

gent channel in which there exists a strong adverse pressure gradient.

However, there would not be boundary layer separation for a flow over a

flat plate at a zero attack angle since the pressure gradient is always kept

negative, and the laminar boundary layer formed close to the leading edge

grows and changes to a turbulent passing through a transition region, when

the plate is sufficiently long.

Fig. 6.22 Boundary layer separation and vortex formation

351

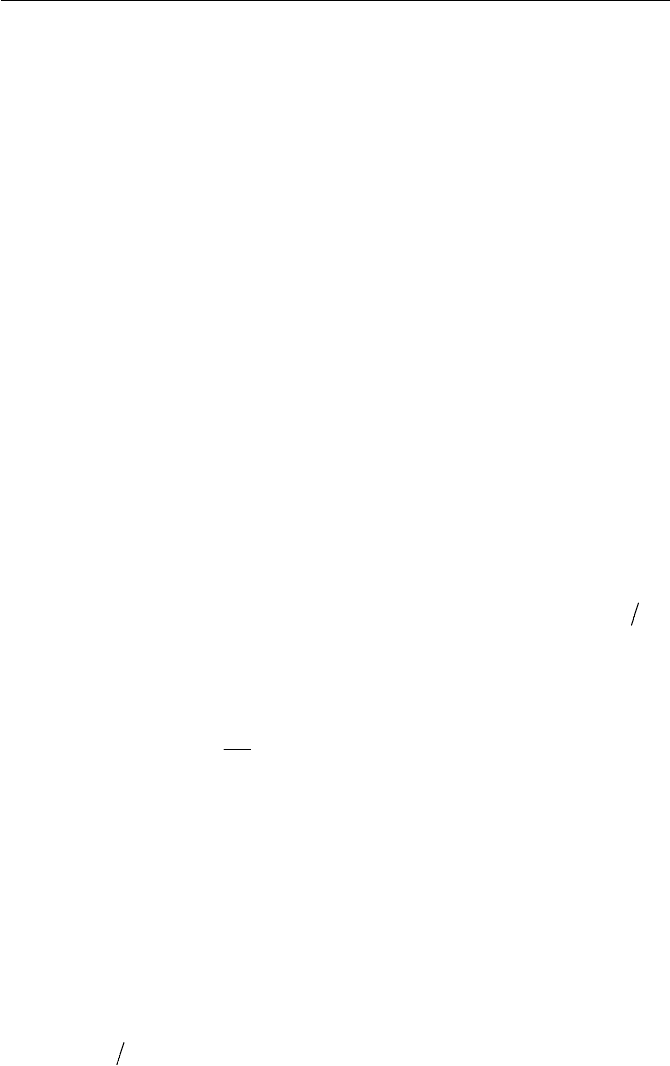
6 Newtonian Flow

The very important phenomenon of boundary layer separation can be

more clearly explained by considering the flow around a circular cylinder,

as illustrated in Fig. 6.22(b). In consideration of an inviscid fluid, the flow

is accelerated on the upstream cylindrical surface, a to b, and decelerated

on the downstream surface, b to c. The adverse pressure gradient occurs in

the region of b to c and the boundary layer below the inviscid flow would

separate at point s on the cylindrical surface. As illustrated in Fig. 6.22(b),

after the point s, backward flow in vicinity of the wall, due to higher pres-

sure in flow direction and toward flow in the upper layer of separation a

streamline causes the vortex formation. The separation point is predicted at

the angle of qt 90

with the boundary layer theory based on inviscid

outer flow. However, for viscous flow, the situation is somewhat different

from the inviscid flow case. For example, at a Reynolds number

of 9500 Re (based on radius

), the angle of separation point s is ap-

proximately q| 580

(Hiemez, experiment 1911), which is quite different

from the inviscid flow. The boundary layer approximation gives a first or-

der estimate, but is inadequate in the separated flow since a large scale

separation may alter the flow field greatly.

The vortex generated in the vicinity of the separation point s is in-

creased in size and becomes separated shortly afterwards and sheds from

the wall, regularly and alternately from opposite sides. The resulting flow

downstream, in the wake, is often referred to as a Kàrmàn vortex street.

dURe

1000040 dd Re , and is accompanied by turbulence. In order to quantify

the vortex shedding, dimensional analysis may be applied by defining the

Strouhal number where

(6.5.39)

where f is the frequency of shedding the vortices. The dimensional

analysis yields, so that St is a function of the Reynolds number and can be

expressed by an empirical relation



7.191198.0



 ReSt

(6.5.40)

for the range of

102250 udd Re . As found in Eq. (6.5.40), St ap-

proaches to the value of 0.198 as the Reynolds number becomes high.

Therefore, the frequency f is directly proportional to the velocity

and

inverse of the diameter

d for a large Reynolds number, i.e.



dUf 1980.|

It occurs in the Reynolds number (based on diameter,

352

6.5 Laminar Boundary Layer Theory

Vortex shedding from an object (such as a cylindrical object) in a flow

may cause periodic lateral forces, when the frequency of a vortex shedding

is equal to the natural frequency of the object. The phenomenon of reso-

nance may occur in the object, appearing as the aerodynamic vibration.

The engineer must be very careful to be aware that such an aerodynamic

vibration can cause a failure of structures, such as towers, chimneys, sus-

pension wire-bridge, and so forth. Furthermore, a long continuous aerody-

namic vibration may cause metal fatigue, leading structures to malfunction.

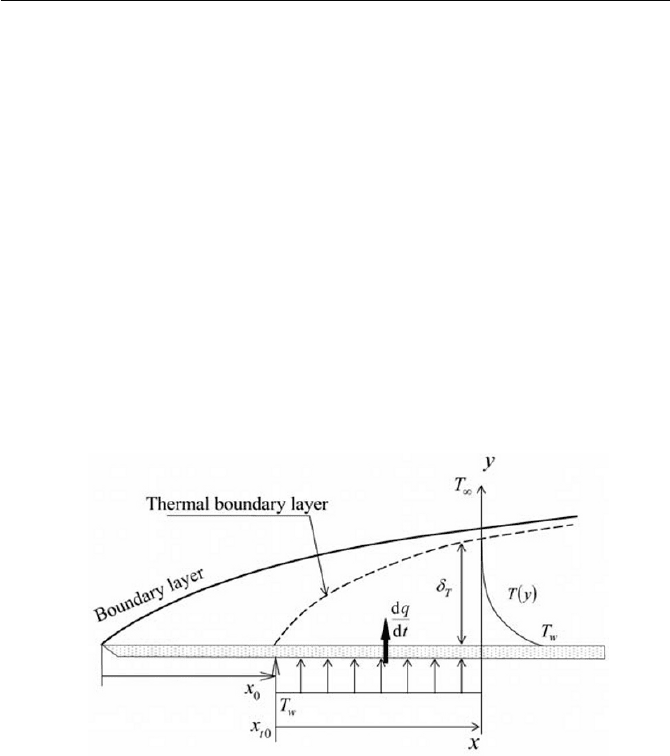
6.5.4. Integral Relation for Thermal Energy

In the case of heating on a flat plate, the energy equation is used to esti-

mate local values of heat transfer and the associated thickness of a thermal

boundary layer. The basic concept of the development of a thermal bound-

ary layer is sketched in Fig. 6.23, where the flow is heated at a constant

temperature with

T beginning at the point of

x .

Fig. 6.23 Thermal boundary layer

In order to derive an expression for the thermal boundary layer, we must

first look into the energy equation where there is a heat transfer from the

plate to the flow in the vicinity of the wall. The nondimensionalized en-

ergy equation in Eq. (6.2.34), will be written in two dimensional

– y co-

ordinates system, assuming the flow is incompressible and the thermal

conductivity

k of fluid is kept constant, as follows

353