Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

6 Newtonian Flow
1
2
**
u
(6.4.22)
It should be kept in mind that the negative pressure gradient is adopted to
make
*
u a positive quantity. Eq. (6.4.22) can now be solved for
1
1
¸
¸
¹
·
¨
¨
©
§
*
*
*
**
dr
du
r
dr
d
r
(6.4.23)
with the boundary conditions,
0
*
u (no-slip at wall) for 1
*
r
(6.4.24)
and
finite
*
u
(along the axis of symmetry) for
0 r
(6.4.25)
The solution of Eq. (6.4.23) is expressed by
21
2
ln
4
1
CrCru
***
(6.4.26)
and with the boundary conditions
0
1
C
and
41
2
C
, we can write a rig-
orous solution for
z
u as follows
2
2
0
0
4
1
rr
z
p
u
z
¸
¹
·
¨
©
§
w
w
K
(6.4.27)
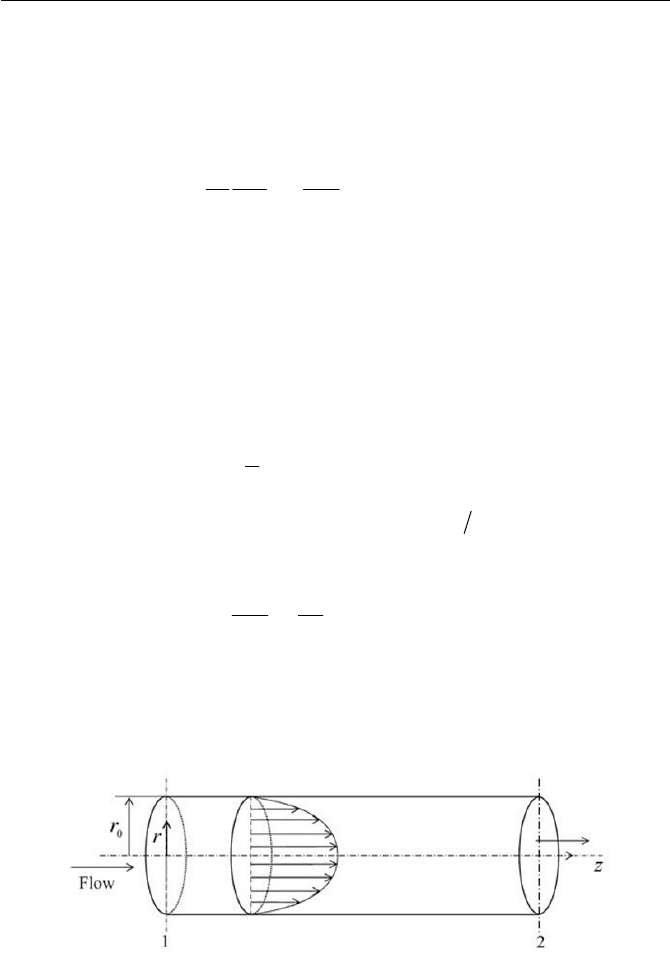
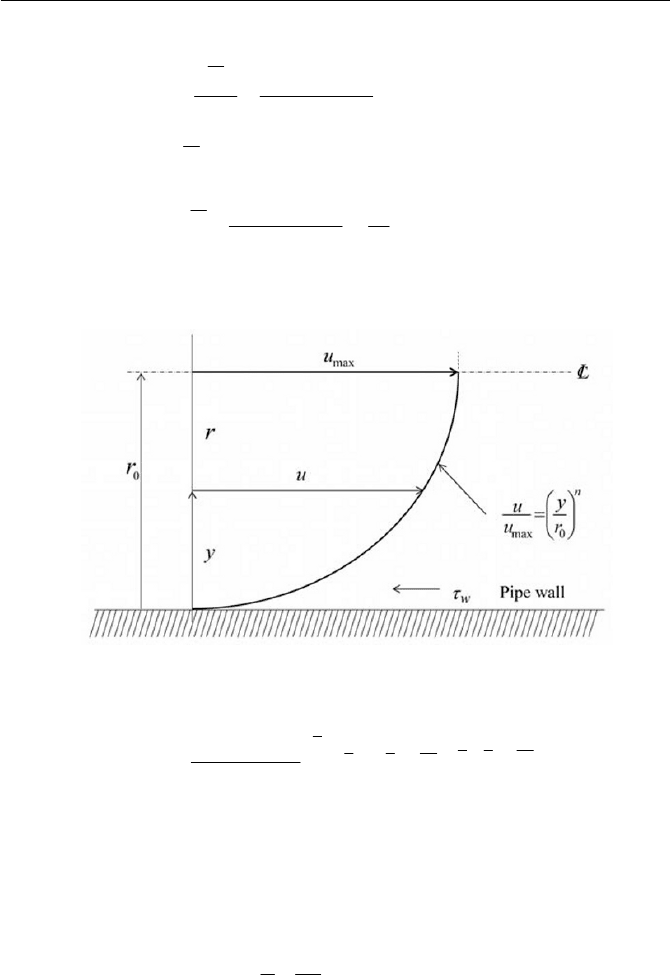
The velocity profile in Eq. (6.4.27) is a paraboloid, termed as the
Poiseuille paraboloid of a revolution about the axis of pipe, as shown in
Fig. 6.10. Note that Eq. (6.4.27) carries a dimension. The flow expressed
in Eq. (6.4.27) is called the Hagen-Poiseuille flow.
Fig. 6.10 Poiseuille paraboloid
Now, the flow properties associated with the Hagen-Poiseuille flow are
examined, knowing that the flow is fully developed that at any cross sec-
324

tion of the pipe, the flow profile is kept identical.
r
dz
dp
r
u
z
rz
¸
¹
·
¨
©
§
w
w
0
2
1
K
W
(6.4.28)
and the wall shear stress
w
W
is calculated by setting
0
rr
0
0
2
1
0
r
z
p
rr
rz
w
¸
¹
·
¨
©
§
w
w
K
WW
(6.4.29)
The volume flow rate
Q through the cross sectional area is given
where
4
0
0
0
0
8
2
r
z
p
rdruQ
r
z
³
¸
¹
·
¨
©
§
w
w
K
S
S
(6.4.30)
This is called the Hagen-Poiseuille equation, and the average velocity
U
is thus given as
2
0
0
2
0
8
1
r
z
p
r
Q
U
¸
¹
·
¨
©
§
w
w
KS
(6.4.31)
The maximum velocity
max,z
u occurs at
0 r
, i.e. at the axis of the pipe,
to write
2
0
0
max
4
1
r
z
p
u
z
¸
¹
·
¨
©
§
w
w
K
,
(6.4.32)
The velocity profile given in Eq. (6.4.27) can be alternatively written by
U or
max,z
u as follows
2
0
12
¸
¸
¹
·
¨
¨
©
§
r
r
Uu
z
(6.4.33)
or
2
0
max
1
¸
¸
¹
·
¨
¨
©
§
r
r
uu
zz ,
(6.4.34)
The pressure drop in an arbitrary section
L with reference to Fig. 6.9
is given in Eq. (6.4.20), and the integration gives
6.4 Flow Through Pipe 325
6 Newtonian Flow
cL
dzcpp
z
z
³
2
1
12
so that
L
p
L
pp
z
p
c
w
w
21
(6.4.35)
Note that Eq. (6.4.35) is equivalent to Eq. (6.4.15). With the aid of Eq.
(6.4.31), the pressure drop
p can be expressed in the following form
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
2
00
0
2
1
22
64
U
r
L
Ur
p
U
UK
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
2
164
U
d
L
Re
U
(6.4.36)
From the Darcy-Weisbach equation below
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
2
1
U
d
L
p
UO
(6.4.37)
the (Darcy) friction factor
O
is thus given in Eq. (6.4.36) as
Re
64
O
(6.4.38)
When the wall of shear stress
w
W
given in Eq. (6.4.29) is non-
dimensionalized as is commonly used in the literature, the skin-friction co-
efficient
f
c (or Fanning friction factor) is defined in such a way that
O
U
W
4
1
2
1
2
U
c
w
f
(6.4.39)
The friction factor
O
derived from the Poiseuille parabolic, namely the
solution of the fully developed laminar pipe flow, is in a generally good
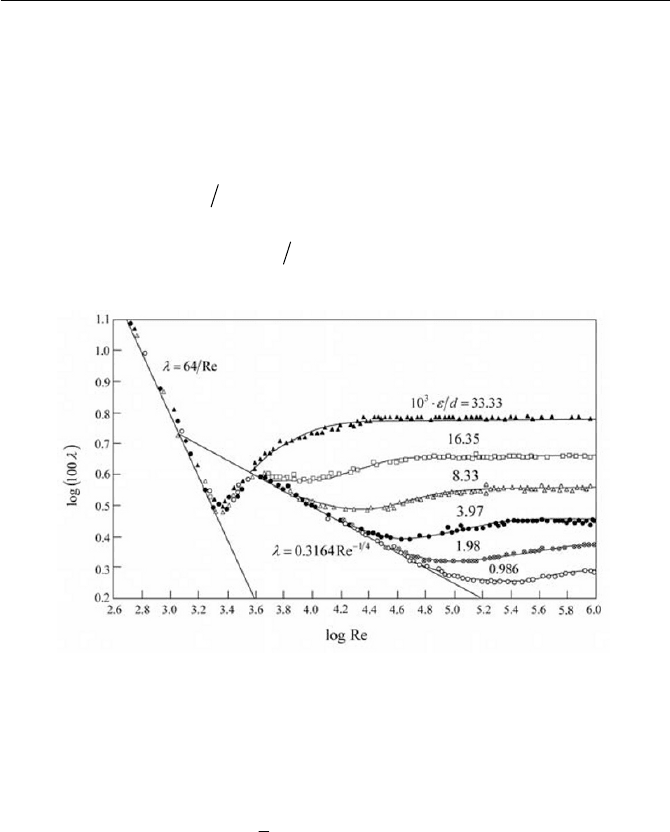
agreement with the experiment as compared with the data (Nikuradse
1933) in Fig. 6.11 with the relationship between
O
and Re . When the
Reynolds number exceeds approximately 2300, in most of engineering ap-
plications, the flow undergoes a transition to turbulence, and above ap-
proximately 3000 the pipe flow becomes fully turbulent. There is no rigor-
'
'
'
'
326
ous solution for turbulent flow in a pipe, where
O
in Eq. (6.4.37) is cus-
tomarily extended in the turbulent flow regime, as shown in Fig. 6.11. It
should be mentioned that Fig. 6.11 is based on experimental data obtained
from various degrees of roughness of a pipe wall (after Nikuradse experi-
ments with pipes of sand roughness), where
H
is the roughness (R.M.S)
and d is the diameter of pipe. As effects of the roughness are exemplified
in the diagram, when
d
H
increases,
O
raises, indicating a higher pressure
drop (higher wall shear) in the turbulent regime, whereas in the laminar re-
gime, as
O
is expressed by Re64 , there would not be the effect of the
roughness on the pressure drop.
Fig. 6.11
O
vs
Re
in straight pipe (replotted after Nikuradse, 1933)
With hydrodynamically smooth pipes that are independent of the sur-
face roughness, a curve fitted correlation to a turbulent flow date is given
as
53
4
1
10103for 31640 ᨺu
ReRe.
O
(6.4.40)
The empirical equation (6.4.40) is called the Blasius formula (1913) that
only depends on the Reynolds number, and is often used for practical pur-
poses in engineering. There are several empirical relations for
O
in hydro-
dynamically smooth pipes. Among those, Prandtl’s universal law of fric-
tion for smooth pipes is valid for a wide range of Reynolds numbers in
turbulent flows, which is given as
6.4 Flow Through Pipe 327
6 Newtonian Flow
80log2
1
.
O
O
Re
(6.4.41)
¸
¸
¹
·
¨
¨
©
§
O
H
O
Re
d
359
log2141
1
.
.
(6.4.42)
It is of interest to know the velocity profile for fully developed turbu-
lent flows in a circular pipe from experimental verifications. This can be
reduced from the Blasius formula (6.4.40) with the definition of the skin-
friction coefficient in Eq. (6.4.39) as follows
2
8
U
w
U
O
W
(6.4.43)
4
1
31640
X
O
dU
.
(6.4.44)
Substituting Eq. (6.4.44) into Eq. (6.4.43) yields
w
W
as
4
3
4
7
4
1
0
4
1
0
033260
UKW
Ur
w
.
(6.4.45)
If we, as Blasius suggested, assume the power law velocity profile for
axisymmetric fully developed a turbulent flow, as schematically shown in
Fig. 6.12, we can write
n
r
y
u
u
¸
¹
·
¨
©
§
0max
(6.4.46)
where
max
u is the maximum velocity at the axis of the pipe, rry
0
is
the wall distance and n is the power index to be determined. It is noted
that u is the time average velocity here in Eq. (6.4.46). The volume flow
rate Q is then calculated as
³
0
0
2
0
2
r
rdruUrQ )(
SS
dyyr
r
y
u
n
¸
¹
·
¨
©
§
0
0
max
2
S
(6.4.47)
C.F. Colebrook (1939) extended the relationship to include the roughness
effect for commercial pipes, which is written as
328
³
0
0
r
Thus
21
2
max
nnu
U
(6.4.48)
and in Eq. (6.4.46),
U can be written as
n
y
r
u
nn
U
¸
¸
¹
·
¨
¨
©
§
0
21
2
(6.4.49)
Substituting Eq. (6.4.49) into Eq. (6.4.45), we have
Fig. 6.12 Power law for turbulent velocity profile
4
7
4
3
4
7
4
7
4
1
0
4
1
0
4
7
21
2
03326.0
n
n
w
yur
nn
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¿
¾
½
¯
®
UKW
(6.4.50)
It should be reasonable to think that
w
W
depends only on fluid properties
and the velocity profile
u so that
w
W
would not include the effect on the
radius
0
r
in its formulation. This thought would lead to the fact that the
power of
0
r in Eq. (6.4.50) is null, i.e.
0
4
7
4
1
n
(6.4.51)
And thus, we can obtain
n for
6.4 Flow Through Pipe 329

6 Newtonian Flow
7
1
n
(6.4.52)
Consequently, the velocity profile
u is written as
7
1
0
7
1
0max
1
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
r
r
r
y
u
u
(6.4.53)
The formula given in Eq. (6.4.53) is termed as the
71 power law of a tur-
bulent velocity profile. By using Eq. (6.4.48), it can be shown that the av-
erage velocity
max
u are related as
max
60
49
uU
(6.4.54 )
The turbulent velocity profile near the solid wall will be further ex-
tended in consideration with the boundary layer theory, which is studied in
later sections.
The time development of flow at the rest to the Poiseuille flow can be ob-
tained as an exact solution of a reduced Navier-Stokes equation. Consider
a Newtonian flow likewise, as in the previous sections, which are initially
at rest in an infinitely long horizontal pipe with a radius
0
r . We will exam-
ine the transient behavior where a constant pressure gradient
dzdp
is ap-
plied at 0 t .
The governing equation of this system is such that, i.e. in the cylindri-
cal axisymmetric rectilinear system, without the body force
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
r
u
r
r
u
z
p
t
u
zzz
1
2
2
0
KU
(6.4.55)
where
z
u is a function of both
r
and t , i.e.
truu
zz
, . Similar to Eqs.
(6.4.23), (6.4.55) can be nondimensionalized through the following re-
lations
6.4.3 Transient Hagen-Poiseuille Flow in Pipe
330

.
0
r
r
r
*
,
t
r
t
r
t
2
0
2
0
0
XUK
*
and
zpr
u
u
z
ww
2
0
0
4
K
*
(6.4.56)
The resultant nondimensional equation can be written in the following
form
*
*
*
*
*
*
*
r
u
r
r
u
t
u
w
w
w
w
w
w
1
4
2
2
(6.4.57)
For the transient Poiseuille flow from at rest, the initial and boundary con-
ditions to be imposed in Eq. (6.4.57) are
0,
***
tru for
0
*
t
,
10 dd
*
r
****
max
, utru for
0!
*
t
,
0
*
r
0,
***
tru for
0!
*
t
, 1
*
r
(6.4.58)
In order to obtain the analytical solution of Eq. (6.4.57), we decompose
z
u with the steady state Poiseuille flow (for f t ) and the transient term
z
u
c
as follows
trurr
z
p
tru
zz
,,
c
¸
¹
·
¨
©
§
w
w
22
0
0
4
1
K
(6.4.59)
which is rewritten in a nondimensional form
***
p
uru
2
1
(6.4.60)
r
u
rr
u
t
u
ppp
w
w
w
w
w
w
1
2
2
(6.4.61)
2
1, rtru
p
for 0 t , 10 dd r
max
1, utru
p
for
0!t
,
0 r
0, tru
p
for 0!t , 1
r
(6.4.62)
Equation (6.4.61) can be solved by using a separation of the variable
in the following manner
6.4 Flow Through Pipe
Equation (6.4.57) is then written in terms of
*
p
u
after the substitution of Eq.
(6.4.60) as follows
It is noted that for a sake of simplicity
will be dropped from the
equation in (6.4.61). The new boundary conditions of Eq. (6.4.61) are
331

6 Newtonian Flow
tTrRtru
p
,
(6.4.63)
so that we have two ordinary differential equations:
0 T
t
dT
(6.4.64)
0
1
2
2
R
dr
dR
r
dr
Rd
(6.4.65)
The solution in Eq. (6.4.64) is rather straightforward to give
t
eTT
0
(6.4.66)
whereas Eq. (6.4.65) is a Bessel’s differential equation of a general form
01
1
2
2
¸
¸
¹
·
¨
¨
©
§
R
r
n
R
r
R
(6.4.67)
rYcrJcR
nn 21
(6.4.68)
The solution
rJ
n
, which has a finite limit as
0or
, is called a Bessel
function of the first kind. The solution
rY
n
, which has no finite limit as
0or , is called a Bessel function of the second kind. The solutions for
rR and
tT are thus obtained with the boundary conditions (6.4.62),
where we have
trurtru
p
,1,
2
¿
¾
½
¯
®
¦
f
1
0
1
1
32
2
81
n
t
nnn
n
erJJr
O
OOO
(6.4.69)
as
0
J and
1
J are the zero-th and first order of Bessel’s function, which are
generated by the following recurrence formula
rJrJrJ
r
n
nnn 11
2
(6.4.70)
and for the
n positive integer we have
d
where 0
tn . It is known that the general solution of the Bessel’s equation
is given in the following form
332
222
6
22
4
2
2
0
642422
1
rrr
rJ
(6.4.71)
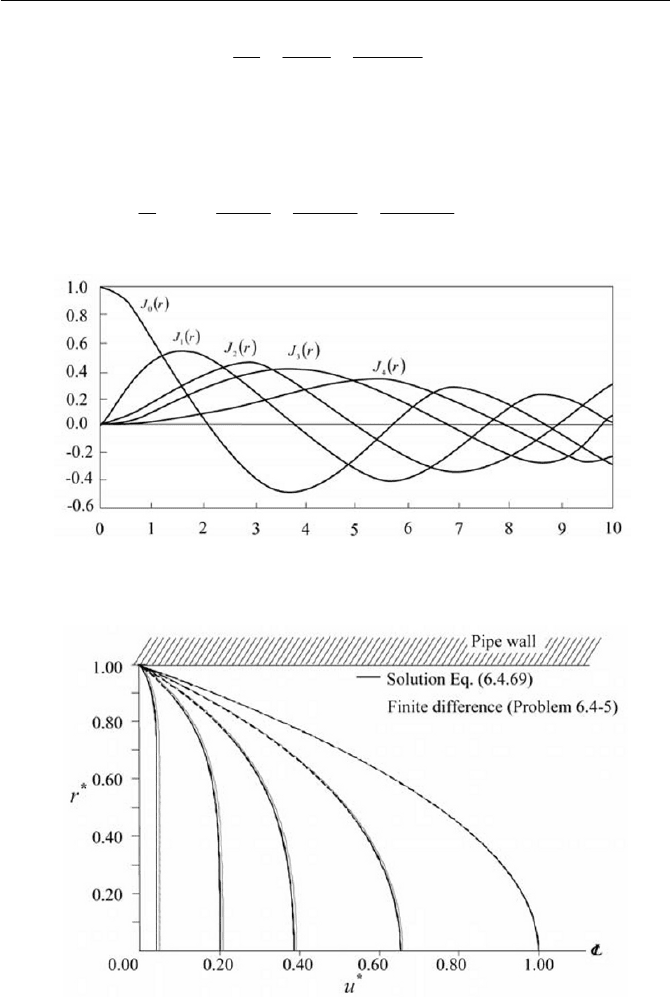
In Fig. 6.13, some
rJ
n
are displayed for a reference.
n
O
that appeared in
(6.4.69) is the
nth root of
0
0
O
J , which are given as
°
¿
°
¾
½
°
¯
°
®
642
15
15116
3
622
1
4
mmm
m
n
SSS
S
O
(6.4.72)
Fig. 6.13 Bessel’s function of first kind
Fig. 6.14 Transient Poiseuille flow
6.4 Flow Through Pipe
333
