Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


6 Newtonian Flow
and then it is solved with the boundary conditions in Eqs. (6.3.29) and
(6.3.30), giving the solution:
rrr
rr
r
rr
rr
u
1
2
1
2
2
21
2
2
2
1
2
1
2
2
1
2
1
2
2
2
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
ZZZZ
(6.3.32)
Among a number of situations in combination of
1
Z
and
2
Z
, we shall ex-
amine a case where 0
2
Z
, i.e. the outer cylinder being kept stationary, as
is often the case in engineering applications. We have a solution from Eq.
(6.3.32) that says
¸
¸
¹
·
¨
¨
©
§
r
r
r
rr
r
u
2
2
2
1
2
2
1
2
1
Z
(6.3.33)
The shear stress
1w
W
acting on the wall of the inner cylinder is
T
W
r
and it
is calculated by
1
01
rr
rw
r
u
r
r
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
w
w
KWW
T
1
2
1
2
2
2
2
0
2
Z
K
¸
¸
¹
·
¨
¨
©
§
rr
r
(6.3.34)
The net torque
r
T exerted on the inner cylinder, whose length is l , is ob-
tained as
1
2
1
2
2
2
2
2
1
0
1
1
l
4
2
Z
SK
SW
l
rr
rr
rlrT
w
r
¸
¸
¹
·
¨
¨
©
§
(6.3.35)
It is useful to mention that Eq. (6.3.35) gives a principle of Couette
rheometer and, with that, the viscosity
0
K
is obtained by measuring the
torque
r
T for the various shear rate
J
with the known geometry
1
r ,
2
r
and
l as follows
>@
¸
¸
¹
·
¨
¨
©
§
J
S
ZS
K
1
4
4
1
2
2
1
2
2
1
2
2
2
21
0
lr
T
rrr
rrT
r
r
)(
)(
(6.3.36)
304

6.3 Basic Flows Derived from Navier-Stokes Equation
where
r
k is the radius ratio
21
rr and
J
is the shear rate defined as
rr
r
kk
k
|
11
1
2
1
2
ZZ
J
(for small gap as 1
o
r
k )
(6.3.37)
In the case of the lubrication of a rotating shaft, the power
P
to over-
come the resistance of viscosity of a lubricant is obtained by multiplying
the torque
r
T by the rotational speed
1
Z
, where
2
1
2
1
2
2
2
2
2
1
0
1
4
Z
SK
Z5
l
rr
rr
T
r
¸
¸
¹
·
¨
¨
©
§
(6.3.38)
The power
5
is normally dissipated into heat and thus results in a tem-
perature increase. The removal of heat from the lubricant often requires
heat exchangers. For a rheometer, the temperature of a test liquid must also
be controlled since
0
K
is a function of temperature.
The laminar flow solution in Eq. (6.3.33) for the inner cylinder rotation
with a fixed outer cylinder is valid up to a rotational Reynolds number
r
Re
,
approximately 7000 (or Taylor number
Ta , 1700|
c
Ta ). Above the criti-
cal value of approximately 7000
|
rc
Re , the flow mode changes from a
simple unidirectional flow to a flow with a secondary flow in the merid-
ional plane, where the velocity distribution in the gap changes with the ap-
pearance of strong
r
u and
z
u components. The flow phenomena was first
tern in the meridional plane, called the Taylor vortex, which is schemati-
cally depicted in Fig. 6.3(b). The occurrence of the flow phenomena is due
to the flow instability. Numerous flow modes appear after the incipience of
the Taylor vortex, when the rotational speed is increased further from
rc
Re
,
and eventually the flow becomes turbulent. These flow transitions are also
observed by plotting the torque coefficient
t
c for the rotational Reynolds
number
r
Re (or Ta ), as indicated in the graph in Fig. 6.3(b).
2
1
5
1
ZU
r
T
c
r
t
(6.3.39)
UK
Z
/
0
1211
r
rrr
Re
(6.3.40a)
or
studied by G.I. Taylor (1923), and found that there appears a cellular pat-
305
6 Newtonian Flow
2
0
3
12
1
3
1
UK
Z
/
rrr
Ta
(6.3.40b)
It must be noted that for measuring the viscosity
0
K
in Eq. (6.3.36) one
should be aware of the limitation of the validity (
r
Re < 7000). It is also
mentioned that the case is different, in view of the flow instability, when
the outer cylinder is rotated while the inner cylinder is kept stationary. The
unidirectionality of
T
u
is kept for further higher Reynolds numbers, since
the flow in the gap is stable in the laminar flow regime.
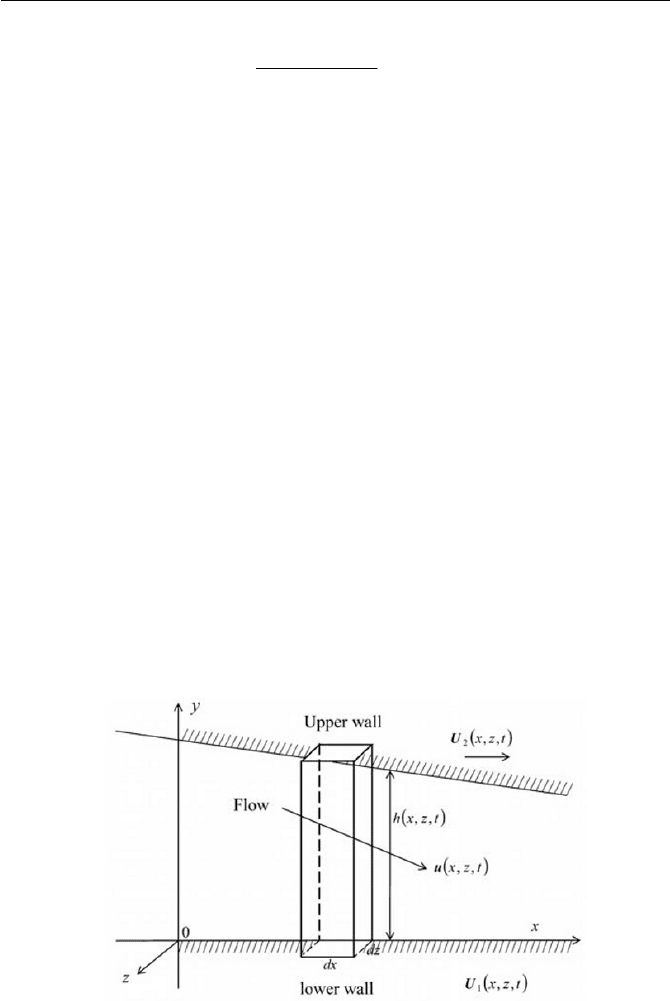
6.3.2 Lubrication Theory
Flow in a varying gap of space is generally regarded as a superposition of
the plane of Couette flow and the plane of Poiseuille flow. Lubrication
flows are generally accomplished by a thin film of viscous fluid in such a
moving wall channel. The theory of lubrication is generally applicable to
the processing of materials in liquid form, film coatings, mechanical lubri-
cation on the slipper-pad bearings and others. The theory was first devel-
oped by Reynolds (1886). The general Reynolds equation in a general lu-
brication problem can be derived for a flow between the upper and lower
walls under the assumption that 1
h , which may be moving tangentially
or normally as schematically displayed in Fig. 6.4, by means of the control
volume principle on the mass continuity equation.
Fig. 6.4 Lubrication flow in a gap
306

6.3 Basic Flows Derived from Navier-Stokes Equation
Based on Eqs. (2.1.3) and (2.1.5), the integration form of the mass con-
tinuity is written as
0
w
w
³³
VV
dVdV
t
u
UU
(6.3.41)
The integration can be performed for the control volume, i.e.
³
h
dydxdz
0
,
and we can reduce Eq. (6.3.41) to the following form
0
00
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
w
w
³³
dxdzdydxdzdy
t
hh
u
UU
where we have
0
w
w
V
t
h
q
U
U
(6.3.42)
where we assumed that the change of
U
in h height is small due to a thin
film of fluid and
V
q
is the volume flux through the gap, which is defined
as
³
h
V
dy
0
uq
(6.3.43)
The flow velocity
tzx ,,u may be written with reference to the solu-
tion given by Eq. (6.3.10)
1
12
0
2
1
U
UU
u
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
y
h
yhyp
K
(6.3.44)
Substitution of Eq. (6.3.44) into Eq. (6.3.43), and rearranging Eq. (6.3.42),
we get the resultant equation where
t
h
hp
h
w
w
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
U
U
K
U
1
2
0
3
2
1
12
UU
(6.3.45)
Equation (6.3.45) is called the Reynolds equation for lubrication. It is men-
tioned here that
U
may be dropped from the equation for incompressible
fluid although in the case when the variation of density is accounted for, in
such as gas bearings,
U
has to be included.
In an application of the Reynolds equation, i.e. Eq. (6.3.45), consider a
slipper-pad bearing as sketched in Fig. 6.5(a). Let us assume the lower
307
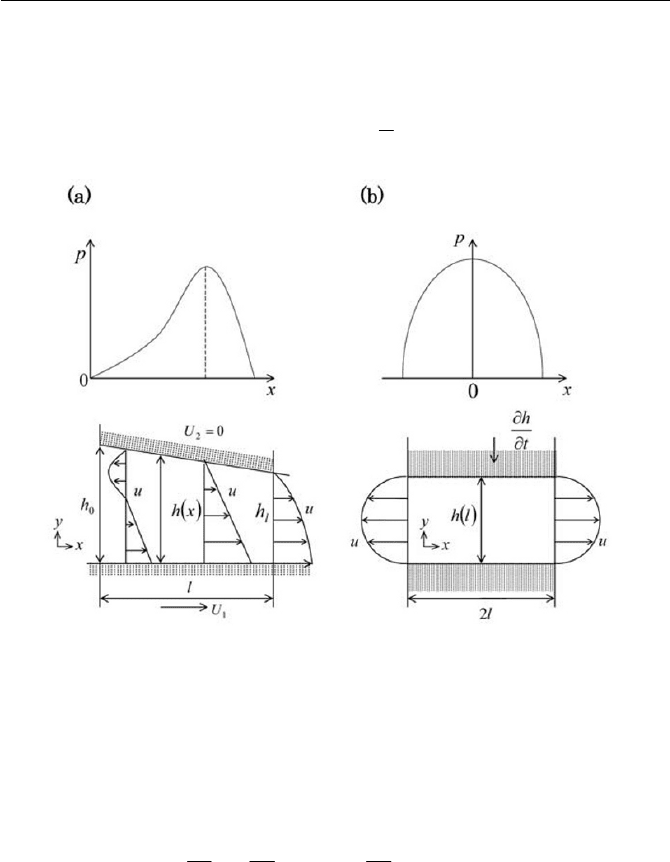
6 Newtonian Flow
wall is flat and moves with a constant velocity of
1
U . The upper wall,
called the slipper block, is inclined where
xh is given by the function
l
x
hhhxh
l 00
(6.3.46)
Fig. 6.5 (a)Slipper-pad bearing
(
(b)Squeezed film
As a bearing, the lubricant fluid provides a high lift force to the slipper
block that supports a large load without the block touching the lower wall
and thus prevents wear. To prove the function, we obtain the pressure force
acting on the block. If we consider the unidirectional (
x
direction), incom-
pressible and steady state flow, Eq. (6.3.45), it can be written as
x
h
U
x
p
h
x w
w
¸
¹
·
¨
©
§
w
w
w
w
1
0
3
6
K
(6.3.47a)
and the boundary condition is such that
0
p at 0 x and 0 p at lx
(6.3.47b)
Equation (6.3.47) is then solved with Eq. (6.3.46) and the boundary condi-
tion which yields the solution to give
308

6.3 Basic Flows Derived from Navier-Stokes Equation
l
l
hhh
xhhU
p
0
2
10
6
K
(6.3.48)
The distribution of
p
as the function of
x
is shown in a graph found in
Fig. 6.5(a), where the velocity profiles
yuu
, which are obtained in Eq.
(6.3.44), are known by given conditions. The total load-bearing capacity
F
(per unit depth) is
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
³
l
l
l
l
l
hh
hh
h
h
hh
lU
pdxF
0
00
2
0
2
1
0
0
2ln
6
K
(6.3.49)
The maximum value of
F
is found by differentiating Eq. (6.3.49) with re-
spect to
l
hh
0
and equating it to zero, and which gives
2
2
10
160
l
max
h
lU
F
K
.
(6.3.50)
where
2.2
0
l
hh . The total drag force
D
F (per unit depth) for the width
l can be calculated as
³
l
wD
dxF
0
W
(6.3.51)
where
0
0
ww
y
w
yu
K
W
, the wall of shear stress.
D
F is obtained by the
known velocity profile, and it is
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
l
l
ll
D
hh
hh
h
h
hh
lU
F
0
00
0
1
0
6ln4
K
(6.3.52)
The drag-lift ratio
max
FF
D
for the maximum load-bearing capacity will
be calculated to give
¸
¹
·
¨
©
§
l
h
FF
D
0
max
142.
(6.3.53)
for
2.2
0
l
hh as a representative value (for maximum load-bearing ca-
pacity).
The slipper-pad bearing is often used as a thrust bearing for heavy tur-
bomachineries, such as for a hydraulic turbine. It is mentioned that revers-
ing the wall direction
01 U
may cause cavitation and form a vapor region
in the gap and may not necessarily exert the required load-bearing capacity.
309

6 Newtonian Flow
The flow configuration of the slipper-pad bearing can be applied to a jour-
nal bearing, where the eccentric annular gap between two rotating cylinder
shafts is filled with lubricant. In the case of a rotating journal bearing,
where the gap contracts and then expands in a rotating direction so that a
partial cavitation often occurs.
The next illustrative example of the Reynolds equation is the squeezed
film problem, which is seen in a squeezed film damper or a modeling of a
knee joint, etc. The basic configuration is displayed in Fig. 6.5(b), where
the upper wall moves toward the lower wall, keeping
h
being parallel to
the both walls. Let us consider the following condition for the problem
t
h
v
w
w
, 0
21
UU and 0 h
(6.3.54)
where the gap width
h is a function of time, i.e.
thh
and the fluid is as-
sumed incompressible. Thus, Eq. (6.3.45) is reduced to
vph
0
23
12
K
(6.3.55)
and for the unidirectional flow of the pressure
p
, we have
v
hx
p
3
0
2
2
12
K
w
w
(6.3.56)
Equation (6.3.56) is directly solved for
p with the boundary condition of
0 x
, 0
w
w
x
p
; symmetry
lx r
, 0 p ; boundary
so that the solution
p
is given as
22
3
0
6
xl
h
v
txp
K
,
(6.3.57)
The pressure distribution
txp , is sketched in the graph in Fig. 6.5(b),
which shows the parabolic distribution. The velocity profile in the gap is
essentially the plane Poiseuille flow as also indicated in the figure, which
is easily verified from Eq. (6.3.44). The total load capacity
F
(per unit
depth) exerted on the upper wall (or the lower wall) is
3
3
0
0
8
2
l
h
v
pdxF
l
K
³
(6.3.58)
310
6.3 Basic Flows Derived from Navier-Stokes Equation
that can be produced by the squeezing of the film flow on the gap walls.
To convey the essence of the subject, although it is hard to survey all
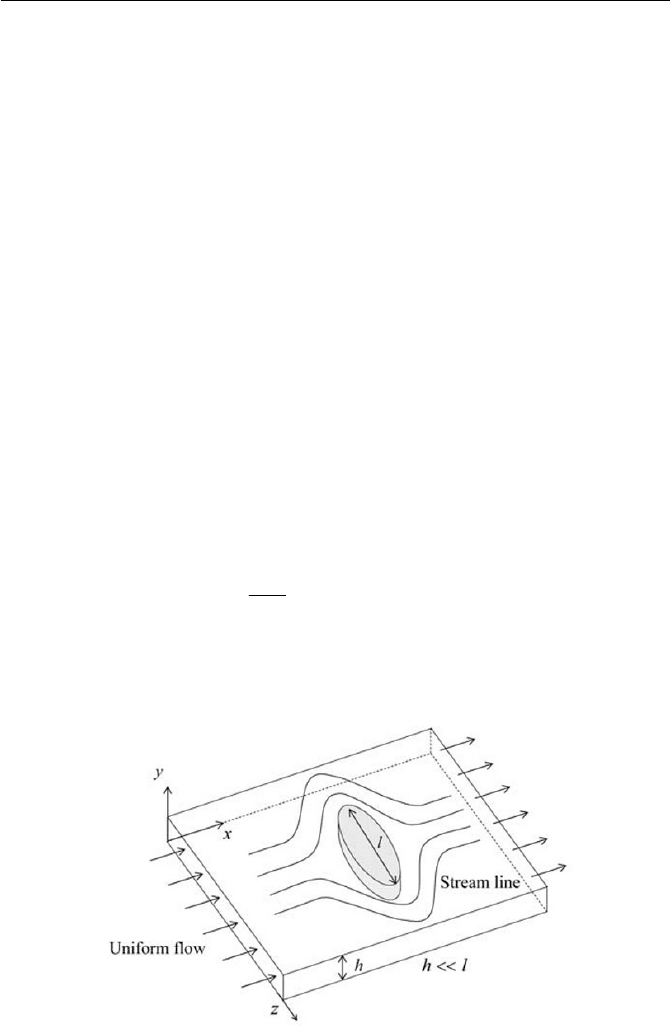
the interesting possibilities, we are able to introduce an interesting applica-
tion of the Reynolds equation, the so-called Hele-Shaw flow. The flow has
a nature of a viscid potential flow, which observes streamline patterns of a
potential flow in laboratory demonstrations. The flow is provided in a
Hele-Shaw cell, that is made of two stationary parallel transparent plates
with a precise small gap distance
h , as shown in Fig. 6.6. When an object,
whose characteristic length
l
is much larger than
h
to ensure a no-slip
condition on the object surface, is placed in the cell, a two dimensional po-
tential flow around the object appears for an incompressible fluid, entering
the cell from one end at a uniform rate. This phenomena is found in the
fact that the pressure
p
in the cell is considered to be followed from Eq.
(6.3.45) where
0
2
p
(6.3.59)
where
U
and h are assumed constant with
0
21
UU
. Thus, the corre-
sponding velocity field is, from Eq. (6.3.44), obtained to write
pyhy
0
2
1
K
u
(6.3.60)
Equation (6.3.60) indicates that in plan view, i.e. the
x
z plane, the stream-
ient, through which the rotation
Fig. 6.6 Hele-Shaw flow cell
–
lines are in parallel with the pressure grad
of Eq. (6.3.60) yields
Since
1h
and if
h
is the decreasing function of t , the total load capac-
ity increases drastically as
foF , indicating a large suspending force
311

6 Newtonian Flow
0
2
1
0
u u pyhy
K
u
(6.3.61)
Therefore, the two dimensional flow field is irrotational and
u can be de-
scribed by a scalar potential (velocity potential)
I
in xz plane, such that
I
u , where
p
itself acts as the velocity potential, satisfying the
Laplace’s equation in Eq. (6.3.59).
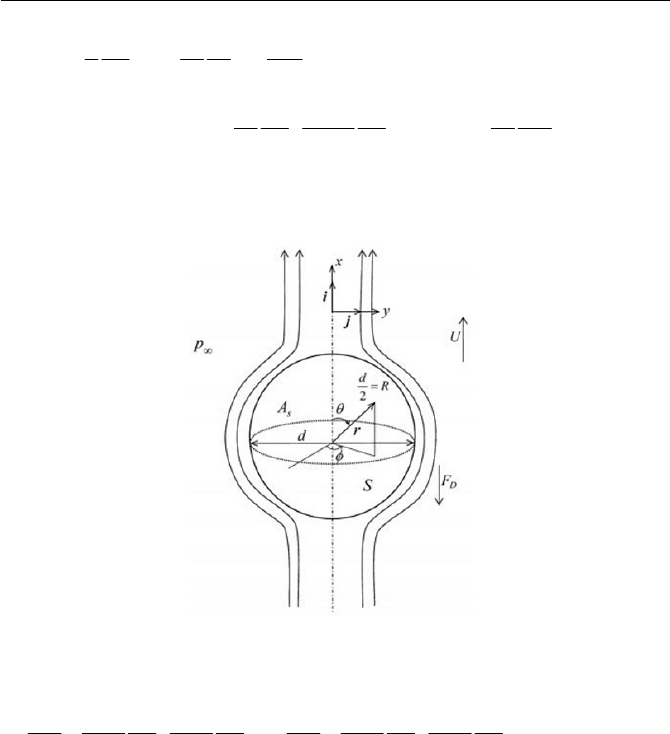
6.3.3 Flow Around a Sphere
Consider a small sphere descending in a viscous fluid. The falling sphere
attains a so-called terminal velocity, when the acceleration becomes zero
after sometime from the incipient motion. In the situation where the buoy-
ant force plus the drag force on the sphere consequently become equal to
its gravity force.
Defining the Reynolds number
UK
0
UdRe
, where d is the di-
ameter of the sphere,
U the terminal velocity,
0
K
the viscosity of fluid
and
U
the density of fluid, we will obtain the drag force and show it to
measure the viscosity of fluid, noting
s
U
being the density of the material
of the sphere. The discussion is supposed to be valid for approximately
1.0
Re .
Let us begin to consider an axisymmetric flow around a sphere, as de-
picted in Fig. 6.7. Due to the axisymmetric flow field where 0
I
u is in
the spherical coordinates system, the flow field can be described by the
stream function
T
\
,r (the Stokes stream function), which identically
satisfied the continuity equation of incompressible fluid. The velocity
components of
r
u and
T
u are thus written by
\
as
rr
u
r
u
r
w
w
w
w
\
TT
\
T
T
sin
1
sin
1
2
,
(6.3.62)
The Navier-Stokes equation in
r
and
T
coordinates, without inertia terms,
i.e. the creep flow limit and neglecting the gravity acceleration, are written
as
»
¼
º
¸
¹
·
¨
©
§
w
w
w
w
«
¬
ª
w
w
w
w
T
T
TT
K
r
r
u
r
ur
rrr
p
sin
sin
11
0
2
2
2
2
2
0
(6.3.63)
and
312
6.3 Basic Flows Derived from Navier-Stokes Equation
»
¼
º
w
w
¸
¹
·
¨
©
§
w
w
w
w
«
¬
ª
¸
¹
·
¨
©
§
w
w
w
w
w
w
T
T
TTT
K
T
T
T
r
u
r
u
rr
r
u
r
rr
p
r
22
2
2
0
2
sin
sin
11
11
0
(6.3.64)
Substituting
r
u and
T
u in Eq. (6.3.62) into Eqs. (6.3.63) and (6.3.64) and
eliminating the pressure terms, we can obtain
Fig. 6.7 Creeping flow past a sphere
0
sin
1sin
sin
1sin
22
2
22
2
»
¼
º
«
¬
ª
¿
¾
½
¯
®
¸
¹
·
¨
©
§
w
w
w
w
w
w
¿
¾
½
¯
®
¸
¹
·
¨
©
§
w
w
w
w
w
w
\
TTT
T
TTT
T
rrrr
(6.3.65)
and using the differential operator
2
E
, we can alternatively write
0
22
\
(
(
(6.3.66)
or
0
4
\(
(6.3.67)
The solutions in Eq. (6.3.66) or Eq. (6.3.67) are harmonic functions in
polar coordinates systems,
T
\
\
,r , with the following boundary con-
ditions on the sphere
313
