Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


6 Newtonian Flow
The components of the Navier-Stokes equation are found in the Ap-
pendix B, together with the equation of continuity and the equation of en-
ergy conservation.
As another point of correspondence, it will be shown that alternative
forms of the Navier-Stokes equation of incompressible flow can be consid-
ered, taking into account the secondary flow field variables, such as the
vorticity vector, for certain problems when pressure and the gravity condi-
tions are not defined explicitly in the boundary conditions. In such a flow
system, conservation equation of the vorticity can be obtained by taking
the rotation of the linear momentum equation and substituting the devia-
toric stress of Newtonian fluids into the vorticity transport equation (2.2.9)
with the following procedure
eIJ
0
2
K
(6.1.9)
IJu
w
w
uȦȦu
Ȧ
UUU
t
(6.1.10)
and resultantly we have
ȦuȦȦu
Ȧ
2
0
w
w
KUUU
t
(6.1.11)
The first term appeared in the right hand side of Eq. (6.1.11) can be further
reduced to
^`
TT
uuuuȦuȦ
2
1
Ȧe Ȧ
ȦȦȦ u e
e Ȧ
(6.1.12)
Therefore, using the relation of Eq. (6.1.12) into Eq. (6.1.11), we obtain
the vorticity transport equation of Newtonian fluid for an incompressible
flow as
ȦȦȦu
Ȧ
2
0
w
w
KUUU
e
t
(6.1.13)
The left hand side terms imply the time change and convection of vorticity
respectively. The right hand side terms represent vorticity amplification
284

Problems
due to the local rate of strain e and diffusion of vorticity with the viscosity
as a diffusivity coefficient respectively. It is interesting to see that the first
term in the right hand side of Eq. (6.1.13) leads to the concept of strain in a
vortex line. The vortex line, as mentioned in Section 4.1, is a line that is
instantaneously formed, joining every point aligned with
Ȧ ; the stream
line is similarly aligned with
u
. The vortex lines are either extended or
contracted, depending on
eȦ . With mass conservation, it is seen that ex-
tended vortex lines move closer together, while contracted lines move fur-
ther apart. A detailed presentation of vorticity dynamics is given in Wu
et al. (2006).
Problems
6.1-1 Write the mass continuity, Navier-Stokes, and energy equations of
incompressible flow in
x
– y plane in Cartesian coordinates system.
Ans.
»
¼
º
«
¬
ª
w
w
0 and 0 with 9B and 8,B 6,BAppndix
z
u
z
6.1-2 Write the mass continuity, Navier-Stokes, and energy equations of
incompressible flow in
r
– z plane in cylindrical coordinates sys-
tems, assuming that the flow is uni-directional and axisymmetric.
Ans.
»
¼
º
«
¬
ª
w
w
0 and 0 with 9B and 8,B 6,BAppndix
T
T
u
6.1-3 Write the mass continuity, Navier-Stokes, and energy equation of in-
compressible flow in
r
–
T
plane in a spherical coordinates system,
assuming the flow is axisymmetric to an axis of rotation through the
center.
Ans.
»
¼
º
«
¬
ª
w
w
0 with 9B and 8,B 6,BAppndix
M
6.1-4 Write the vorticity transport equation of Eq. (6.1.13) in
x
– y plane
in Cartesian coordinates system, assuming that the velocity field is
expressed by the stream function and that the only non-zero vorticity
component is
z
Z
Ans.
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
w
w
x
u
y
u
yxy
u
x
u
t
yx
zz
z
y
z
x
z
\\
ZZ
X
ZZZ
,
2
2
2
2
–– –
–– –
–– –
285
6 Newtonian Flow
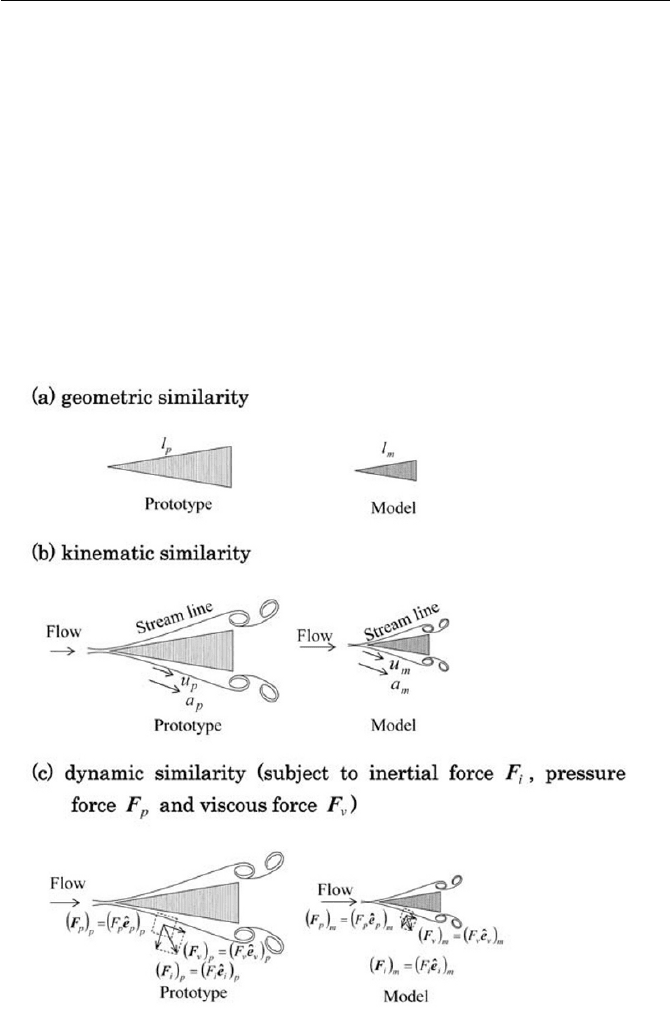
6.2 Similitude and Nondimensionalization
In the design of fluid machineries and systems, before constructing the
full-size device or system, called a prototype, we exploit experimental
modeling as a fundamental method. With the same idea in the solution of
many fundamental fluid mechanics problems, theoretical analysis with a
fluid flow approach is valid only for a limited number of simple problems,
so that in these circumstances we have to depend on test results obtained
from experimental modeling as well. Models, which are usually smaller in
size than the prototype, are tested. If necessary, with a different kind of
fluid, model experiments are utilized for the prototype from the law of
similarity. Similitude is the study of predicting prototype conditions from
model experiments.
Fig. 6.1 Similitude
286

6.2 Similitude and Nondimensionalization
Experimental modeling in the design of fluid machineries and systems
may be found in developing aircrafts in wind tunnels, fluid machineries
and ships in towing tanks, tidal waves in rivers, and so forth. In the simili-
tude there are the similarity conditions to be met in applying test results
obtained from models to the prototype. They are (i) the geometric similar-
ity, (ii) the kinematics similarity, (iii) the dynamic similarity and (iv) the
thermal similarity in some case. The law of similarity for (i) to (iii) are
schematically displayed in Fig. 6.1.
(i) Geometric similarity
The length ratio must be constant between all corresponding points in
the flow fields, when the model and the prototype are identical in shape
but differ in size. Thus, geometrical similarity requires that a scale model
has to have the precise shape of the prototype with the model ratios;
Model ratio
p
m
r
l
l
l
(6.2.1)
Area ratio
2
2
2
r
p
m
p
m
r
l
l
l
A
A
A
(6.2.2)
Volume ratio
3
3
3
r
p
m
p
m
r
l
l
l
V
V
V
(6.2.3)
where subscript
m and
p
denote the model and prototype respectively as
shown in Fig. 6.1(a). The geometric similarity also requires roughness of
objective surface between the model and the prototype. Difference in
roughness may differ with the onset of turbulence, resulting in failure of
similitude. In some problems, however, roughing the surface of the model
may result in holding the geometric similarity. For example, scaling model
of large buildings in a city may face the similar problem, depending on the
magnitude of scaling, i.e. the model ratio scale effect.
(ii) Kinematic similarity
The velocity ratio must be a constant between all corresponding points
in the flow fields for the model and the prototype, where their streamlines
are geometrically similar. In satisfying kinematic similarity, velocities and
287
6 Newtonian Flow
accelerations are in the same ratio for corresponding control volumes in
the flow fields as shown in Fig. 6.1(b);
Velocity ratio
r
r
pp
mm
p
m
r
t
l
tl
tl
u
u
u
(6.2.4)
Acceleration ratio
r
r
pp
mm
p
m
r
l
u
lu
lu
a
a
a
2
2
2
(6.2.5)
or
22
2
r
r
pp
mm
r
t
l
tl
tl
a
(6.2.6)
where
r
t is the time scale ratio. As seen from Eqs. (6.2.4) to (6.2.6), when
the model ratio and the time scale ratio are fixed, the flow will be kine-
maticaly similar. The time scale ratio becomes particularly important for
unsteady flow, indicating that geometrical similarity is not necessarily ki-
nematicaly similar to flows. With satisfying both geometric similarity and
kinematic similarity, we can write the inertial force ratio as
rr
pp
mm
p
i
m
i
ma
ma
ma
F
F
(
6.2.7)
where
r
m is the mass ratio. Equation (6.2.7) shows that the inertial force
ratio becomes constant when the acceleration ratio between corresponding
points on the model and prototype is assured to be constant, if the mass ra-
tio of corresponding control volume is kept constant.
(iii) Dynamic similarity
The forces acting on corresponding control volume in the model flow
and the prototype flow are in the same ratio in the flow fields. Characteris-
tics of the flow fields are governed by the force acting on fluid elements,
so that as seen from Eq. (6.2.7), the kinematic similarity is satisfied when
geometric and dynamic similarities exist between model and prototype
flows.
Suppose that inertial forces
i
F
, pressure forces
p
F
, viscous forces
v
F
,
gravity force
g
F , surface tension forces
s
F and compression forces
c
F
are present in the flow fields of the model and prototype. From Newton’s
288
6.2 Similitude and Nondimensionalization
second law of dynamics, we can equate the inertial force with its summa-
tion if the other forces are
csvpi
FFFFFF
g
(6.2.8)
When all forces are present, dynamic similarity requires that, at corre-
sponding points in the flow fields, the following quotient relation of the
model and prototype should hold
p
c
m
c
p
s
m
s
p
m
p
v
m
v
p
p
m
p
p
i
m
i
F
F
F
F
F
F
F
F
F
F
F
F
g
g
(6.2.9)
These can be rearranged with respect to the inertial force
i
F to read
p
p
i
m
p
i
F
F
F
F
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
,
{
p
i
F
F
Euler number Eu{
(6.2.10)
p
v
i
m
v
i
F
F
F
F
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
,
{
v
i
F
F
Reynolds number Re{
(6.2.11)
p
i
m
i
F
F
F
F
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
gg
,
{
g
i
F
F
Froude number
Fr
{
(6.2.12)
p
s
i
m
s
i
F
F
F
F
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
, {
s
i
F
F
Weber number We{
(6.2.13)
p
c
i
m
c
i
F
F
F
F
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
, {
c
i
F
F
Mach Number
M
{
(6.2.14)
where
Eu , Re ,
Fr
, We and
M
are the nondimensional numbers which
appear in characterizing flow fields. According to dynamic similarity ex-
pressed in Eqs. (6.2.10) to (6.2.14), Newton’s second law given in Eq.
(6.2.8) is expressed in terms of these nondimensional numbers as
c
i
c
s
i
s
i
v
i
v
p
i
p
i
i
i
F
F
F
F
F
F
F
F
F
F
F
F
eeeeee
ˆˆˆˆˆˆ
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
g
g
(6.2.15)
csvpi
M
c
We
c
Fr
c
Re
c
Eu
c
eeeeee
ˆˆˆˆˆˆ
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
54
2
321
g
(6.2.16)
where
i
e
ˆ
~
e
e
ˆ
are unit vectors associated with the forces, as some of them
are representatively shown in Fig. 6.1(c), and
1
c ~
5
c are dimensionless
constants.
289
6 Newtonian Flow
Consequently, to ensure complete dynamic similarity, Eq. (6.2.16) has
simultaneously to be applied to both the model and the prototype system,
where the nondimensional numbers and their associated constants are kept
identical for both systems. For those nondimensional numbers appeared in
Eq. (6.2.16), each nondimensional number is defined by taking
l as the
characteristic length of the system as follows
)(
1
2
2
22
or
vv EuEu
p
U
pl
Ul
F
F
p
i
U
U
(6.2.17)
Re
Ul
Ul
Ul
F
F
v
i
vv
UK
K
U
0
2
0
22
(6.2.18)
)( FrFr
l
U
l
Ul
F
F
g
i
vv or
2
2
3
22
gg
U
U
(6.2.19)
2
0
2
2
0
22
M
K
U
lK
Ul
F
F
c
i
vv
U
U
(6.2.20)
We
l
U
l
Ul
F
F
s
i
vv
UVV
U
222
(6.2.21)
The idea of deriving Eq. (6.2.16) (the dynamic similarity) comes from
the similitude between the model and prototype systems that are com-
pletely ensured if the nondimensional numbers and their associated con-
stants in the governing equations are identical with the same boundary
conditions (satisfying the geometric and the kinematic similarity). We will
see that the nondimensional numbers naturally appear in the governing
equations of flow when the equations are nondimensionalized.
It is mentioned here that nondimensionalization of the flow equations
should also, besides giving the reason of the similitude of dynamic systems,
give two other reasons. The first is that the number of physical parameters
desired to solve the flow problem can be reduced drastically. Thus, there
will be less work involved in solving the equations for given parameter
ranges. This is particularly advantageous in CFD. The second reason is to
give a clue to make rational simplification to the flow equations. This is
particularly advantageous to gain approximation solutions based on order-
of-magnitude arguments in some flow problems.
With the same process the dynamic similarity applied to the momen-
tum equation of Eq. (6.2.8), we are able to obtain the nondimensional
290

6.2 Similitude and Nondimensionalization
cussed in the previous section in dealing the second coefficient of viscosity
0
O
, we will ignore the u
0
O
term identically, thereafter. The mass conti-
nuity equation and the Navier-Stokes equations are written respectively as
0
w
w
u
U
U
t
(6.2.22)
g
UKU
¸
¹
·
¨
©
§
w
w
uuu
u
2
0
p
t
(6.2.23a)
or
g
UKU
u
u
2
0
p
Dt
D
(6.2.23b)
Nondimensionalization of Eqs. (6.2.22) and (6.2.23) is accomplished by
dividing both side of the equations by an appropriate combination of char-
acteristic dimensions. Particularly, for the momentum equation, i.e. the
Navier-Stokes equation (force per volume) of Eq. (6.2.23), the division is
done by the inertial force dimension, thereby making each term dimen-
sionless. By common variables of characteristic dimension, we choose
l
as a characteristic length,
U as characteristic velocity,
0
U
as characteristic
density,
0
p as characteristic pressure and
0
t as characteristic time. We
firstly write nondimensional parameters (denoted by asterisk) by scaling
quantities with the characteristic dimensions as
l
x
x
*
,
0
t
t
t
*
(and
l
tU
t
*
)
U
u
u
*
,
0
p
p
p
*
,
0
U
U
U
*
i
i
*
ˆ
x
l
e
w
w
ේ ,
i
i
x
l
e
ˆ
2
2
22*
ේ
w
w
(6.2.24)
Thus, by using those nondimensional parameters, Eqs. (6.2.22) and
(6.2.23) can be reduced to
¸
¹
·
¨
©
§
0
U
l
U
¸
¸
¹
·
¨
¨
©
§
w
w
***
*
u
U
U
ේ
t
0
(6.2.25)
governing equations for Newtonian fluids. For the sake of simplicity, as dis-
291
6 Newtonian Flow
g
g
eu
u
u
ˆ
****
***
*
*
*
U
U
K
U
U
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¿
¾
½
¯
®
w
w
¸
¹
·
¨
©
§
2
2
0
0
2
0
0
0
ේ
U
l
Ul
p
U
p
u
t
Ut
l
(6.2.26)
Using notation by Eqs. (6.2.17) to (6.2.21), we can write Eqs. (6.2.25) and
(6.2.26), by dropping an asterisk * for brevity’s sake, as
0
w
w
u
U
U
t
(6.2.27)
g
euuu
u
ˆ
2
2
ේ
1
ේ
1
FrRe
p
Eut
St
U
U
¸
¹
·
¨
©
§
w
w
(6.2.28)
where UlUtlSt
Z
is identified as the Strouhal number (=centrifugal
force/inertial force). Note that for a periodic flow motion (
Z
as angular
velocity), such as vortex shedding (for example, flow past cylinder, flow
through turbomachinery, etc.), it is necessary to model the effect of perio-
dicity, which is in effect included with the Strouhal number. With a similar
process, the Navier-Stokes equation in non-conservation form may be
simply written as, instead of Eq. (6.2.28)
g
eu
u
ˆ
2
2
ේ
1
ේ
1
FrRe
p
EuDt
D
U
U
(6.2.29)
Equation (6.2.29) is the same formulation defined in Eq. (6.2.16).
There are some variations on the nondimensionalizing Navier-Stokes
equation, however, depending upon the systems and how those character-
istic parameters are to be chosen.
For example, in natural convection, there is no characteristic velocity
defined in fluid flow systems, where flow is driven by a buoyant force due
to a small change in density. In such a system, the density can be linearly
approximated with respect to the temperature change as
^`
00
1 TT
T
|
E
U
U
(6.2.30)
where
T
E
is the coefficient of thermal expansion defined by Eq. (2.5.25).
The characteristic velocity
U can be replaced by
l
0
U
K
. A new non-
dimensional number may appear for a natural convection, when the Na-
vier-Stokes equation is appropriately simplified, where the non-
dimensional number is given in
292
6.2 Similitude and Nondimensionalization
'
2
0
2
0
0
2
0
X
U
U
K
UE
33
l
g
l
g
TT
Gr
T
Grashof number
(6.2.31)
The derivation of nondimensionalized Navier-Stokes equation, with a
Boussinesq approximation, is given in Exercise 6.2.1.
Up to this point we have dealt with flow problems in which the tem-
perature was assumed constant. However, when the heat and work transfer
to the fluid system are to be considered, the energy equation has to be
coupled with the momentum and the mass continuity equation. Thermal
similarity between the model and the prototype system, or more specifi-
cally for a scaled experiment, is treated with the same manner. This is
done straightforwardly, by nondimensionalizing the energy equation of Eq.
(2.5.24) to give
Dt
Dp
TTk
Dt
DT
c
Tcp
EU
(6.2.32)
where
uේ:IJ is the dissipation function and the heat transfer
Tk
c
q (Fourier’s law) is assumed by a conduction, knowing that the
internal heat generation term
b
U
in Eq. (2.5.24) is ignored. Note that
c
k
is the reference thermal conductivity. Nondimensional parameters (de-
noted by an asterisk) are defined by scaling quantities with characteristic
dimensions as
0
0
TT
TT
T
w
*
,
2
2
U
l
K
*
(6.2.33)
where
w
T is the boundary temperature and
0
T the reference temperature.
Using quantities in Eqs. (6.2.33) and (6.2.24) that are substituted into Eq.
(6.2.32), the final result of the energy equation takes the following form,
after dropping the asterisk
Re
Ec
Dt
Dp
EcT
PrReDt
DT
2
1
(6.2.34)
Nondimensional numbers appeared in Eq. (6.2.34) other than in Eq.
(6.2.29), such as
0
2
Tc
U
Ec
p
Eckert number
(6.2.35)
or alternatively, for an ideal gas (denoting
k as the specific heat ratio. i.e.
)
)
)
)
293
