Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

6 Newtonian Flow
vp
cck )
^`
2
2
0
2
0
2
0
2
0
2
111
1
Mk
a
U
k
kRT
U
k
TkkR
U
Tc
U
Ec
p
D
X
K
kk
c
Pr
c
p
0
Prandtl number
(6.2.36)
PrRePe
Peclet number
(6.2.37)
PrEcBr Brinkman number
(6.2.38)
Thus, taking into account new nondimensional numbers in Eq.
(6.2.34), the similitude of the two systems, i.e. the model and prototype,
can be held when the temperature field is considered.
Solving Eqs. (6.2.27);
u
=0 for incompressible flow, Eqs. (6.2.28 or
6.2.29) and (6.2.34) with given boundary conditions, would give similarity
solutions that represent flow fields of any similar systems simultaneously.
It is seen from the nondimensionalized governing equations that choosing
the nondimensional numbers controls the flow fields of the systems. Thus,
the similarity solutions are the function of the nondimensional numbers,
represented as
0,,,, PrEcFrEuRef
(6.2.39)
where
Re , Eu ,
Fr
, Ec and P
r
are the nondimensional numbers that
appeared in the governing equations discussed above.
In the study of engineering fluid mechanics, there are very few prob-
lems that are actually solved using the differential equations discussed
above and have the similarity solutions as represented by a form of Eq.
(6.2.39). Instead of actually solving the system of differential equations,
we may be able to adopt dimensional analysis to predict prototype condi-
tions from model observations that are based on the notion of dimensional
homogeneity. With dimensional analysis we can find essential non-
dimensional numbers, which contributes to similitude with the two sys-
tems. The Buckingham
S
-theorem is a very powerful tool to derive the
essential nondimensional numbers. Particularly in experimental studies in
fluid mechanics involving the use of scaled models, the
S
-theorem is ef-
fective for correlating experimental results. In Appendix C, the Bucking-
ham
S
-theorem is demonstrated. The reader may refer to the point that
the nondimensional numbers obtained in Eq. (6.2.16) are also straightfor-
wardly derived by the
S
-theorem.
294

Exercise
Exercise
Exercise 6.2.1 The Boussinesq Approximation
There are situations of practical occurrence, where the validity of physical
properties in a fluid is due to small variations in temperature. In natural
convection applications of fluid under gravity and buoyancy for variations
in temperature of only moderate levels, the Navier-Stokes equation may
be simplified so as to put buoyancy into evidence. In such a case, we may
treat the density as a constant
0
U
in all terms in the Navier-Stokes equa-
tion of incompressible media, except for the one in the buoyancy term due
to gravity. This is called the Boussinesq approximation. In the energy
equation, the viscous dissipation term can be ignored owing to the fact
that the prevailing velocity field is weak. The basic equations in the Bous-
sinesq approximation are written as
0
u
(1)
g
0
2
00
UUKU
c
u
u
p
Dt
D
(2)
Tk
Dt
DT
c
cp
2
0
ේ
U
(3)
^`
00
1 TT
T
E
U
U
(4)
and
0
I
c
pp
(5)
where
0
I
is the gravitational potential, such as defined by zg
0
0
U
I
in
Cartesian coordinates system.
Nondimensionalize the equations (1) to (3), using the following non-
dimensional parameters
lU
00
UK
uu
u
*
,
0
2
00
KU
l
t
t
t
t
*
,
2
0
2
0
2
0
l
p
U
p
p
UK
U
c
c
*
0
0
TT
TT
T
w
*
where U and
0
t are replaced by
lU
00
U
K
and
0
2
00
K
U
lt re-
)
spectively. Also, consider a heat transfer through a boundary with an ap-
propriate nondimensional number.
295
6 Newtonian Flow
Ans.
The basic equations are nondimensionalized as
0
2
0
0
¸
¸
¹
·
¨
¨
©
§
**
u
l
U
K
(6)*
g
eu
u
ˆ
****
**
**
gT
*
00
2
3
0
2
0
3
0
2
0
3
0
2
0
TT
l
p
ltD
D
l
W
T
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
EU
U
K
U
K
U
K
(7)*
**
**
**
T
l
k
TT
tD
TD
l
c
TT
c
w
p
w
2
2
0
2
0
0
¸
¹
·
¨
©
§
K
(8)*
so that, for nondimensional equations after dropping the asterisk
0
u
(9)
g
eu
u
ˆ
*
GrTp
Dt
D
2
ේේ
(10)
T
PrDt
DT
2
ේ
1
(11)
At a boundary in natural convection, the heat transferred
w
q
(heat
flux) to the fluid is customarily defined such that
w
q is proportional to
w
TTT as
Thq
ww
(12)
where
w
h is called the heat transfer coefficient.
w
h may be non-
dimensionalized either by
Uc
h
TTUc
q
Sn
p
w
wp
w
0
0
0
UU
(13)
where
Sn
is called Stanton number, or
c
w
k
lh
Nu
(14)
where
Nu is called a Nusselt number. Sn and Nu are related by
'
'
296
Exercise
SnRePrNu
(15)
where
Re is defined by the characteristic length l . Thus, from the argu-
ment given above for the natural convection, if
Nu is chosen as a thermal
characteristic parameter, a characteristic in a thermally similar system may
be determined where
PrGrfNu ,
(16)
For a very simple basic system in natural convection, for example,
called the Benard’s convection,
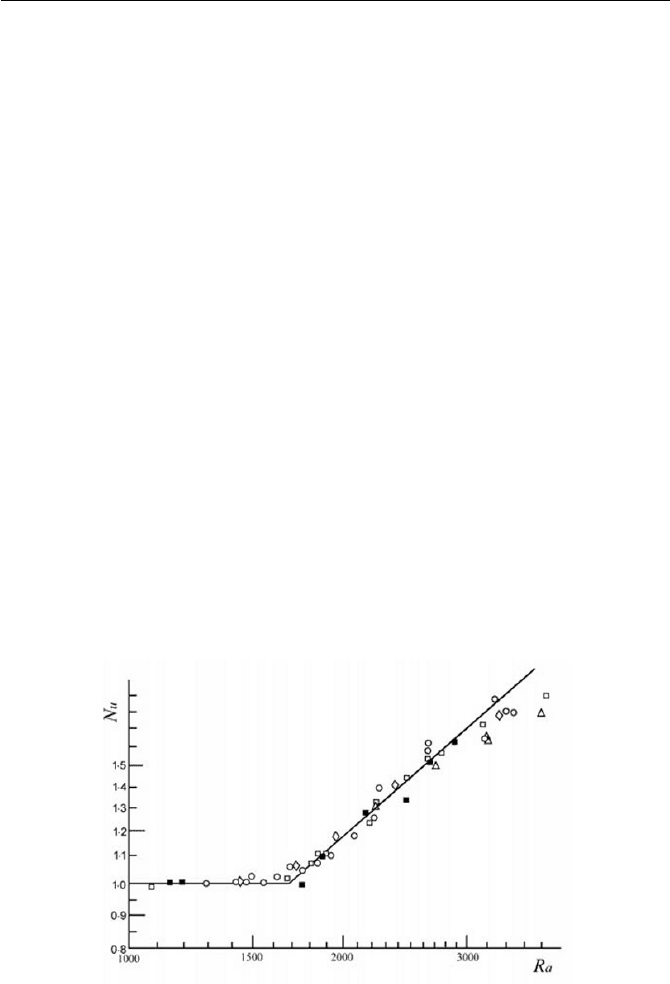
Nu around the onset of a natural convec-
tion from the heat conduction mode is almost a function of
PrGr u , as
show in Fig. 6.2. The data referred in Fig. 6.2 is a case for the Benard’s
convection, where the lower plate is heated while the upper plate is cooled
for fluids contained in an infinite slab. As the experimental results indicate
that
Nu becomes a function of PrGr u , which is defined as a Rayleigh
number, i.e.
PrGrRa u , after the onset of a natural convection that is
observed after
Nu deviates from value of 1 around 1708|Ra , as seen in
Fig. 6.2. The natural convection occurs from a state of equilibrium in heat
conduction mode at the critical Rayleigh number
c
Ra
, where the value of
c
Ra in Fig. 6.2 is approximately 1708|
c
Ra , which is also verified by an
instability analysis. For a limited range of
,Ra it is possible to express the
Nusselt number
Nu by the relationship
RafNu
(
17)
Fig. 6.2 Benard’s convection at onset of natural convection
(Replotted after Silveston, 1958)
297
6 Newtonian Flow
Problems
6.2-1 Give the definition for each nondimensional number in Eqs. (6.2.10)
to (6.2.14);
WeFrReEu ,,, and
M
in view of the dynamic similarity.
6.2-2
For steady state flows in a horizontal pipe of diameter d and length
l with the roughness
H
(RMS), the dominant forces will be the driv-
ing force (pressure), resisting force (wall shear), and the inertial
force. Find the governing nondimensional numbers.
Ans.
»
¼
º
«
¬
ª
H
,,
d
l
Refc
p
6.2-3 A prototype propeller of a wind power generator of diameter 50 m is
to be tested in a wind tunnel using a
501
scaled model. If the proto-
type propeller is to run at 60 rpm, what should be the speed (revolu-
tion per minutes) of the model? What is the ratio of prototype torque
and model torque? The fluid properties for the prototype and model
are the same.
Ans.
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
rpm4245060
22
m
m
mm
d
d
nn
dndn
Fr ,
gg
6.2-4 Assume that the critical Rayleigh number of the natural convection is
1708
c
Ra for an infinite slab. For water as a working fluid, esti-
mate the temperature difference
T between the lower hot surface
and upper cold surface, when the thickness of the slab is 20 mm.
Take a reference temperature at 20
C
$
.
Ans.
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
K116
3
0
0
0
3
0
2
0
0
32
0
.
l
kR
T
k
Tl
k
TTl
PGR
T
a
TT
rra
UE
K
K
UEX
K
UE
D
DD
g
gg ᧩
6.3 Basic Flows Derived from Navier-Stokes Equation
There are certain cases for viscous flows where the Navier-Stokes equation
is rationally simplified so that analytical solutions can be obtained. In the
most of the cases that the analytical solutions are available, the nonlinear
term (the convective term) in the Navier-Stokes equation is either omitted
or linearlized in consideration of the types of flow with appropriate as-
sumptions to avoid further intricate problems.
'
'
'
298

6.3 Basic Flows Derived from Navier-Stokes Equation
We will see a number of basic flows in which such results are valid
within a certain range of Reynolds numbers. In order to gain further engi-
neering significance, some cases are extended to include higher Reynolds
numbers, illuminating pure viscous flow phenomena.
6.3.1 Unidirectional Flow in a Gap Space
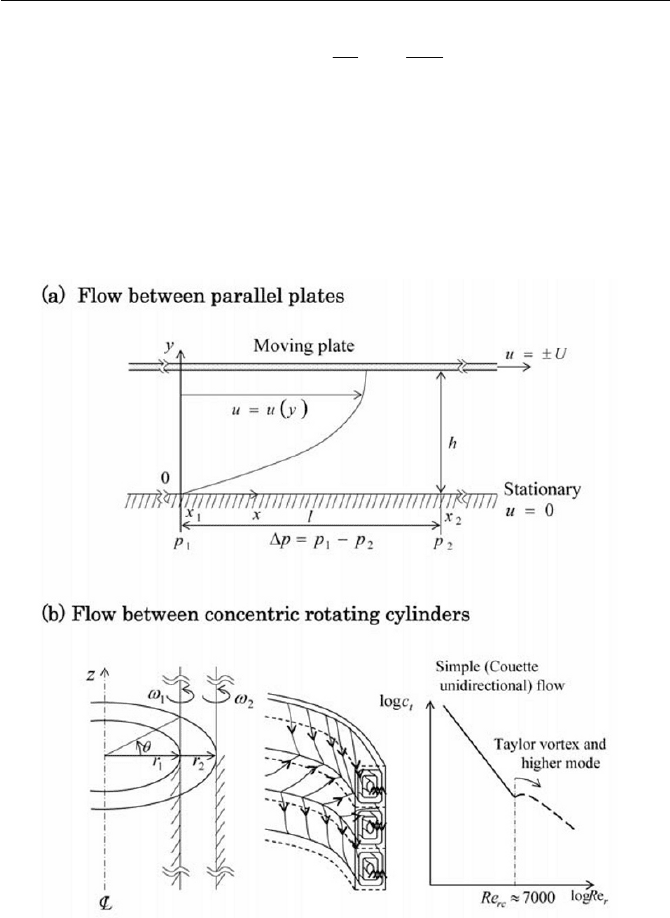
M. Couette (1880) conducted experiments on the flow between stationary
and moving concentric cylinders. Flows in a narrow gap, including parallel
plates and concentric cylinders, are treated here.
(i) Flow in parallel plates is considered firstly as one of the simplest geo-
metrical configuration of flow, referred to Fig. 6.3(a). As schematically
displayed in the diagram, the flow configuration is such that the length of
the gap is
h and the upper plate moves with velocities Uu r , while the
lower plate is kept stationary. Assume that flow is unidirectional to
x
direc-
tion, incompressible and steady, neglecting the body force or may be in-
cluded in
p
as the gravitational potential as previously described. For ex-
ample, the conditions are
0,0,,, uuuu
zyx
{u
(6.3.1)
¸
¹
·
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
{
0,0,,,
x
p
z
p
y
p
x
p
p
(6.3.2)
and
yuu
(6.3.3)
const.
w
w
x
p
(6.3.4)
0
u , 0
w
w
t
, 0 g
U
(6.3.5)
The governing equations of flow in Cartesian coordinates systems are writ-
ten as
Continuity:
0
w
w
x
u
(6.3.6)
299
6 Newtonian Flow
N-S equation:
2
2
0
0
y
u
x
p
w
w
w
w
K
(6.3.7)
The boundary conditions are such that with reference to Fig. 6.3(a)
0
u for 0 y
(6.3.8)
Uu r for hy
(6.3.9)
Fig. 6.3 Flows in narrow gap
The solution in Eq. (6.3.6) is Constant u for
x
direction, indicating
that the flow is fully developed toward its motion.
300

6.3 Basic Flows Derived from Navier-Stokes Equation
Equation (6.3.7) is solved for )(yu with the boundary conditions in
Eqs. (6.3.8) and (6.3.9), giving solutions as
h
Uy
yyh
l
p
u
r
0
2
K
(6.3.10)
where the pressure difference
p between the points in
x
-direction
1
x
and
2
x are defined by, as in Eq. (6.3.4)
c
dx
dp
(constant)
(6.3.11)
so that
1212
xxcpp
clp , 0
21
t ppp
and
l
p
c
(6.3.12)
The solutions (6.3.10) indicate that the velocity profiles appearing in the
flow field is parabolic in nature, and this flow is called the plane Poiseuille
flow, particularly in the case when 0
U . On the contrary, when 1h ,
the second term in Eq. (6.3.10) dominates the flow field, yielding
y
h
U
u r
(6.3.13)
The flow of Eq. (6.3.13) has a linear velocity profile, and is called the
plane Couette flow, which is independent from the viscous effect.
The volume flow rate
Q through the gap is then calculated from Eq.
(6.3.10) such that
212
0
3
0
Uh
l
ph
dyuQ
h
r
³
K
(6.3.14)
and the average velocity
u is also defined by
212
0
U
l
ph
h
Q
u
r
K
(6.3.15)
Using the average velocity
u for the plane Poiseuille flow ( 0 U ), the
flow through the channel (the gap) length
l may be characterized by the
'
'
''
'
'
'
2
301

6 Newtonian Flow
friction coefficient
O
, or referred as Darcy friction factor, defined along
with the Darcy-Weisbach equation
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
1
l
h
p
UO
(6.3.16)
in which
Re
24
O
(6.3.17)
where the Reynolds number
Re
is defined as
UK
0
h
Re
(6.3.18)
It is also desired to derive an expression for the wall shear stress
w
W
to give
h
y
xyw
0
0
6
K
WW
(6.3.19)
which, furthermore, is nondimensionalized as
Re
c
w
f
12
2
1
2
U
W
(6.3.20)
In a similar way, the plane Couette flow is also characterized as follows
Re
4
O
and
R
e
c
f
2
(6.3.21)
The flow expressed with Eq. (6.3.10) is laminar and is maintained up to
the incipience of the turbulent flow mode, in the order of 1000
#Re for
the plane Poiseuille flow and 1900
#Re for plane Couette flow.
(ii) The flow between two concentric rotating cylinders as shown in Fig.
6.3(b) is another flow field that is obtained by solving Navier-Stokes equa-
tion with rational simplification. The geometric configuration of flow is
particularly important for lubrication of a rotating shaft, a cylindrical vis-
cometer and other similar designs. The analytical solution of laminar flow
will be found for fairly slow relative rotational speeds between the inner
cylinder with an angular velocity of
1
Z
and an outer cylinder with that of
2
Z
. Assume that the flow is unidirectional for
T
direction, incompressible
'
2
u
u
u
u
302

6.3 Basic Flows Derived from Navier-Stokes Equation
and steady, neglecting the body force or inclusive in
p
, i.e. the conditions
are
0,,0,, uuuu
zr
T
u
(6.3.22)
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
0,0,,
1
,
r
p
z
pp
rr
p
p
T
(6.3.23)
and
ruu
(6.3.24)
0
w
w
T
u
, 0
w
w
z
u
(6.3.25)
0 u ,
0
w
w
t
, 0 g
U
(6.3.26)
The governing equations of flow in cylindrical coordinates systems are
written as
Continuity :
0
1
w
w
T
u
r
(6.3.27)
N-S equation :
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
22
2
0
1
0
r
u
r
u
r
r
u
K
(6.3.28)
The boundary conditions are such that, with reference to Fig. 6.3(b)
11
Z
ru
for
1
rr
(6.3.29)
22
Z
ru for
2
rr
(6.3.30)
where it is noted that
1
Z
and
2
Z
include the direction r for the laboratory
(fixed) frame of reference.
The solution of Eq. (6.3.27) is
Constant u for
T
direction, indicating
that the flow is fully developed toward its motion.
In order to solve Eq. (6.3.28), it will prove useful to write the equation
with
0
2
2
¸
¹
·
¨
©
§
r
u
dr
d
dr
ud
(6.3.31)
303
