Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

6 Newtonian Flow
0
T
uu
r
for
R
d
r
2
(6.3.68)
which implies
0
w
w
r
\
and 0
w
w
T
\
(6.3.69)
At infinity,
fo
r
TTT
T
T
eeee
ˆˆˆˆ
sincos
rrr
UUUu
(6.3.70)
which implies that
T
\
2
sinUr
r
w
w
and
TT
T
\
cossin
2
Ur
w
w
(6.3.71)
Equation (6.3.71) gives
\
at
for
by the integration of
TT
T
\\
\\
22
sin
2
1
Urddr
r
d
w
w
w
w
³³³
(6.3.72)
Equation (6.3.72) might assume the form of the solution in Eq. (6.3.67) as
T
\
grf
(6.3.73)
In order to seek a solution in Eq. (6.3.67), it may be appropriate to set
TT
2
sin g and substitute Eq. (6.3.73) for Eq. (6.3.64), where
0sin
2
2
2
22
2
¸
¸
¹
·
¨
¨
©
§
T
rf
rdr
d
(6.3.74)
In order to satisfy Eq. (6.3.74) for
r
and
T
simultaneously, we must sat-
isfy
0
2
2
22
2
¸
¸
¹
·
¨
¨
©
§
rf
rdr
d
(6.3.75)
The solutions of f in Eq. (6.3.75) must satisfy the following differential
equation (equidimentional equation)
0884
24
c
cc
cccc
ffrfrfr
(6.3.76)
Equation (6.3.76) is the so-called Euler’s differential equation, to which the
general solution to this equation is given as
314

6.3 Basic Flows Derived from Navier-Stokes Equation
4
4
2
32
1
rcrcrc
r
c
rf
(6.3.77)
where constants
1
c ,
2
c ,
3
c and
4
c are determined from the boundary con-
ditions in Eqs. (6.3.68) and (6.3.69). The final solution in Eq. (6.3.73) is
given with the aid of the functional form of Eq. (6.3.73) where
T\
2
3
3
2
sin
2
1
2
3
1
2
1
¸
¹
·
¨
©
§
r
R
r
R
rU
(6.3.78)
Equation (6.3.78) also gives the velocity components as
T
cos
2
1
2
3
1
3
3
¸
¹
·
¨
©
§
r
R
r
R
Uu
r
(6.3.79)
T
T
sin
4
1
4
3
1
3
3
¸
¹
·
¨
©
§
r
R
r
R
Uu
(6.3.80)
Knowing the velocity field given in Eqs. (6.3.79) and (6.3.80), we can
obtain the pressure field by substituting Eqs. (6.3.79) and (6.3.80) into Eqs.
(6.3.63) and (6.3.64), and carrying out the integration to yield
T
,rp as
³³³
w
w
w
w
f
2
0
cos
2
3
r
RUpd
p
dr
r
p
dprp
T
KT
T
T
,
(6.3.81)
where
f
p is the pressure at infinity, i.e. fo
r
.
As another point of correspondence, it will now be shown that the drag
force
D
F , which is the net force acting on the sphere in the flow direction
i in Fig. 6.7, may be calculated by obtaining the stress component
x
t
on
the sphere in direction
i . This will be done by knowing the stress vector t
on the sphere as follows
jiji
eeIJeet
TTWTTW
WW
T
TT
cossinsincos
rrr
rrrrrr
p
pp
ˆˆ
I
ˆ
T
ˆ
(6.3.82)
The stress component
x
t is thus
T
W
T
W
T
sincos
rrrx
pt ti
(6.3.83)
where
rr
W
and
T
W
r
are components of the viscous stress tensor of a New-
tonian fluid, and which are given by the following constitutive equations
315
6 Newtonian Flow
r
u
r
rr
w
w
0
2
KW
,
»
¼
º
«
¬
ª
w
w
¸
¹
·
¨
©
§
w
w
T
KW
T
T
r
r
u
rr
u
r
r
1
0
(6.3.84)
The velocity components
r
u and
T
u of Eqs. (6.3.79) and (6.3.80) are then
substituted into the relationship in Eq. (6.3.84), and consequently
x
t will
be obtained as
U
R
pt
x
0
2
3
cos
K
T
f
(6.3.85)
Thus, as a result, the drag force
D
F is calculated to integrate
x
t over the
spherical surface
S
dU
RU
ddRtdStF
x
S
xD
0
0
2
00
2
3
6
sin
SK
SK
ITT
SS
³³³
(6.3.86)
It is noted that
T
cos
f
p does not contribute the drag
D
F due to its
symmetry, as previously described, indicating that the potential flow,
which has only a contribution of
T
cos
f
p , does not influence the drag,
but only that the viscous contribution found in Eq. (6.3.85) does in the case
of viscous flow. If the drag coefficient
D
c is defined such that
s
D
D
AU
F
c
2
21
U
(6.3.87)
where
s
A is the frontal area of the sphere. Then we can reduce Eq. (6.3.86)
to give the drag coefficient in terms of the Reynolds number
RedU
F
c
D
D
24
421
22
SU
(6.3.88)
If 10
.Re , which implies a small sphere in a high viscous fluid, the
Stokes’ law is valid and for a sphere at the terminal velocity
U
, the buoy-
ant force
b
F plus the drag force
D
F become equal to the gravity force
g
F ,
that is
Equation (6.3.86) states that at the creep flow limit the drag force is line-
arly proportional to the speed of flow passing a small sphere (or a descend-
ing sphere with a constant speed). This is called Stokes’ law.
316
6.3 Basic Flows Derived from Navier-Stokes Equation
gg
s
dUdd
U
S
SKU
S
3
0
3
6
3
6
(6.3.89)
An important application of Eq. (6.3.89) is to measure the viscosity
0
K
by
measuring the terminal velocity
U for a falling sphere in a transparent cyl-
inder, containing the viscous fluid to be tested. According to Eq. (6.3.89)
0
K
can be obtained where
U
d
s
18
2
0
g
UU
K
(6.3.90)
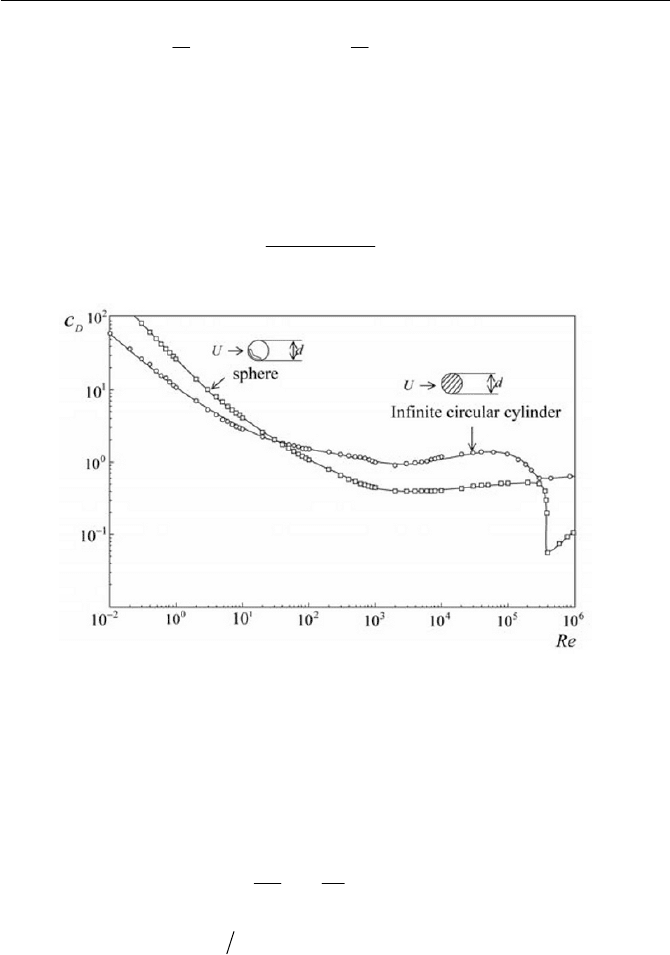
Fig. 6.8
D
Drag coefficient of a sphere and an infinite cylinder
sources, and data for
4
10tRe
is
replotted after Achenback, 1971
and 1972)
The drag coefficient
D
c
given by Stoke’s law, i.e. Eq. (6.3.88), is fur-
ther extended to validate in higher Reynolds numbers by Oseen (1910)
n
D
Re
Re
c
¸
¹
·
¨
©
§
16
3
1
24
(6.3.91)
where 1
Re for sm1 u . If n is chosen at 0.5, Eq. (6.3.91) is extended
to
100|Re . Typical changes of
D
c versus Re are displayed in Fig. 6.8 for
a sphere and an infinite cylinder for the sake of comparison. It is seen in
both cases at approximately
55
105103 uu| ~Re , there is a sudden drop
(From various
317

6 Newtonian Flow
in the value of
D
c . This is due to phenomena caused by a transition of
laminar flow to turbulence. The boundary layer, which is described in
more detail in later sections, is the cause of this phenomenon.
Problems
6.3-1 Describe how the resultant flow between the concentric rotating cyl-
inders can be used as a means of measuring the viscosities of fluids.
Give comments on the feasibility of the method of measuring vis-
cosity.
6.3-2 A slipper-pad bearing is running with a speed of
sm2
1
U
. The rep-
resentative dimensions are such that,
m1080
4
0
u .h
,
m1040
4
u .
l
h
and m30. l . The viscosity of the lubricant oil is
sPa102
5
0
u
K
at a constant operating temperature. Find the total
load-bearing capacity to maintain the gap. Also calculate the drag-
lift ratio.
Ans.
»
»
¼
º
«
«
¬
ª
u
5
max
106550
N354
.
.
FF
F
D
6.3-3 Design an appropriate experimental apparatus for examining a poten-
tial flow around an infinite cylinder.
6.3-4 A small sphere of diameter
d and density
s
U
is dropped from a rest
position in a viscous fluid with density
U
. Write the equation of mo-
tion of this sphere and find the terminal velocity. The viscosity of the
fluid is
0
K
. Assume that the Stokes’ law is in effect to the motion of
the sphere.
Ans.
»
»
»
»
¼
º
«
«
«
«
¬
ª
¸
¹
·
¨
©
§
0for
18
6
3
66
0
3
0
33
dt
dU
U
dUdd
dt
dU
d
s
ss
K
UU
U
S
SKU
S
U
S
2
gd
g-g
6.3-5 Find the time elapsed to the fall distance m010
. l for a sphere of
m101
5
u d and
33
mkg105u
s
U
released from a position of
rest in a viscous fluid of viscosity
sPa101
1
0
u
K
and the density
33
mkg102u
U
.
Ans.
>@
s. 9001 Appox.
318
6.4 Flow Through Pipe
6.4 Flow Through Pipe
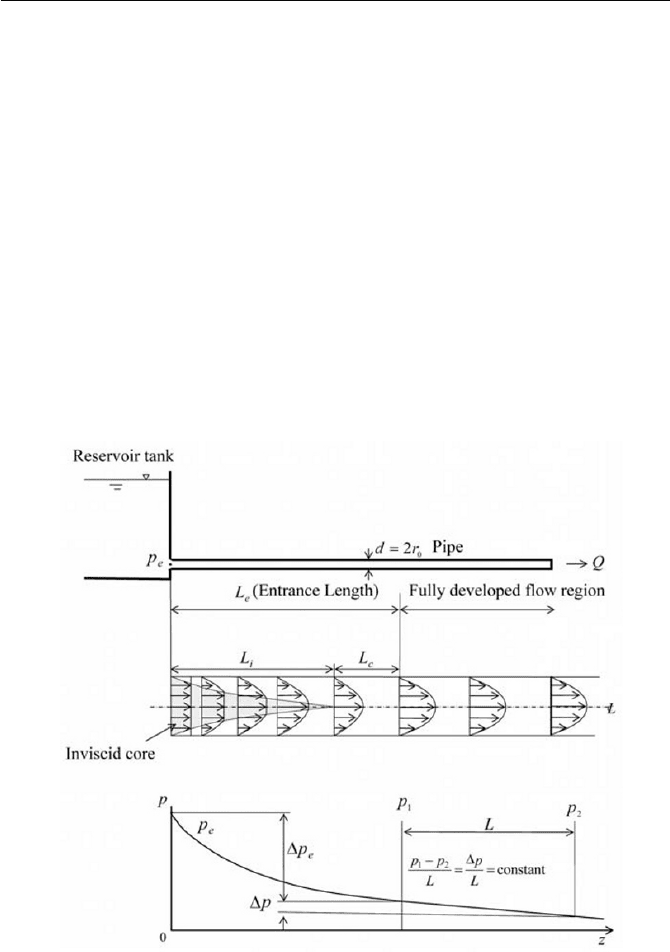
The circular pipe flow is probably the most celebrated viscous flow in the
development of fluid dynamics, in view of the fundamental importance of,
as well as, basic fluid engineering applications. We shall start to consider a
straight circulation pipe connected to a reservoir tank, as illustrated in Fig.
6.9. In many practical engineering applications, a pipe is usually connected
to a reservoir tank or a source, and the flow in the pipe starts to move for-
ward, downstream. Note that the entrance is supposed to be a bell mouth
shape to avoid boundary layer separation. There will be an “entrance ef-
fect”, where a shear layer (boundary layer; details of which will be studied
in later section) on the pipe wall and an inviscid core (uniform constant ve-
locity region along axis of the pipe) that develops toward the downstream
of flow near the entering region of the pipe.
Fig. 6.9 Circular pipe flow though entrance
319
6 Newtonian Flow
As indicated in Fig. 6.9, the shear layer grows and meets at the axis as the
inviscid core disappears within the length
i
L
termed as the inviscid core
length, at which the viscous stress dominates the entire cross section. The
profile then continues to change due to the viscous effect until a developed
flow is achieved, where the length is often termed as the profile develop-
ment region
c
L . The total length
ci
LL is called the entrance length
e
L ,
and after which the flow is fully developed, where the velocity profile
across the cross section does not change toward the downstream.
6.4.1 Entrance Flow
The entrance length for a laminar flow can be correlated in the forms
Re
d
L
e
0650. (Boussinesq, 1891 and Nikuradse, 1933)
(6.4.1)
h
h
e
Re
d
L
05050 .. (Shah and London, 1978)
(6.4.2)
where Reynolds number
Re is based on the average velocity U through a
cross section area and the diameter
d , i.e.
X
dURe . Note that the
Shah-London correlation is valid for an arbitrary pipe shape in a cross sec-
tion, where
h
d is the hydraulic diameter (four times hydraulic radius
h
r ),
which is defined by
h
p
h
r
l
A
d 44
¸
¸
¹
·
¨
¨
©
§
(6.4.3)
where
A is the cross-section area and
p
l is the wetted perimeter, that pe-
rimeter where the fluid is in contact with the solid boundary. The limit of
the Reynolds number is approximately 2300 for engineering applications,
whereas with carefully controlled conditions the Reynolds number may go
up to higher values in excess of 40,000.
For a turbulent flow, the situation is somewhat different from the lami-
nar case. In order to observe the entrance length
e
L
of the fully developed
turbulent flow, an extra length may be needed for the detailed structure of
the turbulent flow to develop in addition to the profile development region.
For the high turbulent strength flow at the inlet of the pipe, the entrance
length
e
L is given by the following correlation at the Reynolds numbers
normally encountered
320

6
1
44 Re
d
L
e
.
4025 ~ (Nikuradse, 1933)
(6.4.4)
The pressure variation along the pipe length from the inlet is sketched
in Fig. 6.9, where the inlet pressure is
e
p . The pressure loss at the entrance
length occurs due to an acceleration of flow, i.e. the kinetic energy loss,
and the viscous friction loss. The pressure loss
e
p solely due to the ki-
netic energy loss can be estimated in consideration of the energy flux at a
representative cross sectional area as follows
Ur
EE
p
ef
e
2
0
S
(6.4.5)
where
f
E
and
e
E are the kinetic energy through a cross section of pipe at
the entrance length
e
L and the inlet respectively. They are, therefore,
given by the following formula
³
¸
¹
·
¨
©
§
0
0
2
2
2
1
r
eandf
rdruuE
SU
(6.4.6)
For the laminar flow, the velocity profile in the fully developed flow is
given by well known Hagen-Poiseuille flow, which will be explained in
the subsequent section (with reference to Eq. (6.4.33)), as follows
2
0
12
¸
¸
¹
·
¨
¨
©
§
r
r
Uru
(6.4.7)
where, at the inlet of the pipe, the velocity profile can be assumed to be
constant where
Uru
(6.4.8)
Substituting Eqs. (6.4.7) and (6.4.8) into Eq. (6.4.6) and calculating
e
p
from Eq. (6.4.5), we can obtain
2
2
Up
e
U
(6.4.9)
If the pressure loss coefficient
]
based on a loss of head is defined by
'
'
'
'
6.4 Flow Through Pipe 321

6 Newtonian Flow
¸
¸
¹
·
¨
¨
©
§
gg 2
2
Up
e
]
U
(6.4.10)
]
is obtained for the laminar flow as
1
]
(6.4.11)
In the case of the turbulent flow,
]
is given by 71 power law (Eq.
6.4.53)
090
.
]
(6.4.12)
The actual pressure loss (defining
0
]
]
as the total pressure loss co-
efficient) at the entrance length is usually higher than that of the kinetic
energy loss due to the viscous friction loss, and they are found by using the
Hagen’s experiments
71
0
.
]
for laminar flow
(6.4.13)
40
0
.
]
without bell mouth entrance for turbulent flow
(6.4.14)
In the flow beyond the entrance length the pressure variation tends to
decrease linearly along the axial distance
z and the pressure gradient
L
p
L
pp
z
p
w
w
21
(6.4.15)
is kept constant for both the laminar and turbulent flows.
For
e
Lz ! , the velocity becomes a solely axial and only with the lateral
coordinates in the fully developed flow in a circular pipe, as sketched in
Fig. 6.9, where the flow is non-accelerating and is driven by the pressure
gradient (when the gravitational body force is ignored for a horizontal
straight pipe or, if at all, it can be incorporated in the pressure term as the
potential energy function). In general terms, such a (nearly) non-
accelerating flow of an incompressible Newtonian fluid in a steady state of
motion is treated as the so-called Stokes’ equation, which is written with
the continuity equation as follows
0 u
(6.4.16)
'
'
6.4.2 Fully Developed Flow in Pipe
322

and
0
2
0
u
K
p
(6.4.17)
It should be noted that the Stokes’ equation (6.4.17) is reduced from the
Navier-Stokes equation Eq. (6.1.7), by setting the inertia term zero, and is
valid for not so large Reynolds number where the flow tends to become
turbulent. The flow field derived from Eq. (6.4.17) is independent of the
density, and the flows followed in Eq. (6.4.17) are so-called creeping flows,
even though the Reynolds number need not be small (and in fact the Rey-
nolds number is not even a required parameter).
It is now desired to consider the fully developed, pressure-driven lami-
nar flow in a circular pipe where the flow is assumed to be steady, axi-
symmetric and rectilinear. This flow is termed as the Hagen-Poiseuille
flow, which implies that in the flow field there is only an axial velocity
component
z
u , while the radial
r
u and circumferential
T
u velocity com-
ponents are, respectively, 0
r
u and 0
T
u . In the cylindrical coordi-
nates system
z
u may be the function of
zr ,,
T
, i.e.
zruu
zz
,,
T
. How-
ever with the condition of axisymmetry, i.e.
0
w
w
T
z
u
(6.4.18)
and from the mass continuity
0
w
w
z
u
z
(6.4.19)
z
u is only the function of
r
, i.e.
ruu
zz
. In the fully developed recti-
linear flows, the pressure gradient in the axial direction is kept constant as
is referred to in Eq. (6.4.15), i.e.
c
z
p
w
w
const.
(6.4.20)
It will prove useful to consider the nondimensionalization of the
Stokes’ equation in Eq. (6.4.17), which can be carried out by taking the
pipe radius
0
r
as follows
0
r
r
r
*
,
zpr
u
u
z
ww
2
0
0
K
*
(6.4.21)
Resultantly we have
6.4 Flow Through Pipe 323
