Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

6 Newtonian Flow
where
14 nm
. The detailed derivation of the solution (6.4.69) is found
in Szymaniski (1932) and Papanastasiou et al. (2000).
As a result of the solution expressed in Eq. (6.4.69), the transient behav-
ior of the flow is shown in Fig. 6.14, where it is seen that two (both ana-
lytical and numerical) flow velocities evolve from a rest position as time
elapses to reach the maximum center speed
10 f,u .
It is mentioned that Eq. (6.4.57) is a partial differential equation of a
parabolic type that is solved numerically fairly easily, such as the finite dif-
ference method. In Fig. 6.14, as an example, a numerical solution by the
finite difference method is displayed in comparison with the analytic solu-
tion of Eq. (6.4.69).
Exercise
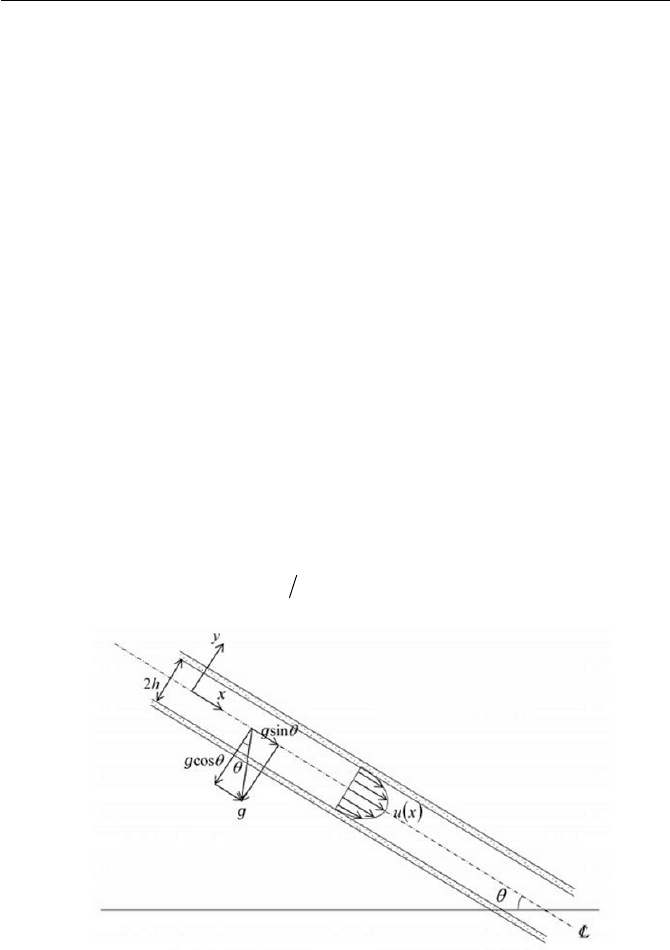
Exercise 6.4.1 Inclined Plane Poiseuille Flow
Let’s us consider the incompressible steady laminar flow between two in-
clined plates as shown in Fig. 6.15. Obtain the velocity profile of
u as a
function of
y for the one dimensional rectilinear flow in
x
– y plane, as-
suming the pressure gradient
xp ww is constant.
Fig. 6.15 Inclined plane Poiseuille flow
334

Exercise
Ans.
The Navier-Stokes equation can be reduced to the following form in the
x
– y plane
TUK
sin0
2
2
0
g
w
w
w
w
y
u
x
p
(1)
With the boundary conditions such that
0
dy
du
for 0 y
(2)
and
0
u for hy
(3)
Equation (1) can be solved for
u , which yields the solution as
22
0
sin
2
1
yh
x
p
yu
¸
¹
·
¨
©
§
w
w
TU
K
g
(4)
The body force (the gravity) is added to the pressure gradient to in-
crease, depending on the sign of
T
sin
.
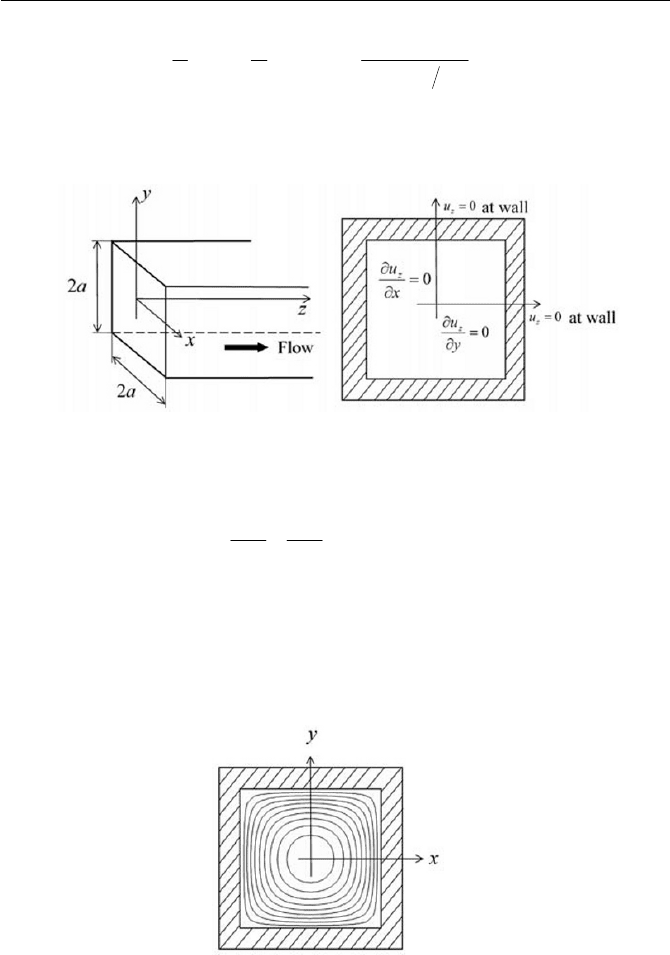
Exercise 6.4.2 Laminar Flow in a Square Duct
Suppose that an incompressible Newtonian fluid is flowing through an in-
finitely long square duct. The flow is assumed laminar with the constant
pressure gradient along the flow direction
z . Determine the velocity pro-
file in the square cross section of the
x
– y plane, as depicted in Fig. 6.16.
Ans.
The situation is that the non-accelerating and unidirectional flow of the
velocity component
z
u
is persisting in the duct with a constant pressure
gradient. We apply the Stokes’ equation given in Eq. (6.4.17) in
z -
direction, so that we can write the governing equation of flow as
z
p
y
u
x
u
zz
w
w
w
w
w
w
0
2
2
2
2
1
K
(1)
Equation (1) can be nondimensionalized by the relationships
335
6 Newtonian Flow
a
x
x
*
,
a
y
y
*
and
zpa
u
u
z
ww
2
0
2
K
*
(2)
through which the resultant nondimensionalized equation for Eq. (1) will
be written as
Fig. 6.16 Flow in a square duct
2
2
2
2
2
w
w
w
w
y
u
x
u
(3)
It is noted that * is dropped in Eq. (3) for a sake of clarity. The boundary
conditions in the first quadrant plane (due to symmetry) are written below.
Note that at the center of the duct the symmetric conditions in both
x
and
y axis are given respectively together with the no-slip conditions at the
wall.
Fig. 6.17 Velocity contour in a duct flow
336

Exercise
0
w
w
y
u
for 0 x
0
w
w
x
u
for 0 y
0 u
for
1 x
0
u for 1 y
(4)
Similar to Eq. (6.4.59), by decomposing
z
u with the plane Poiseuille
flow, we have
yxuya
z
p
yxu
zz
,
2
1
,
22
0
c
¸
¹
·
¨
©
§
w
w
K
(5)
and with a nondimensional form, we can write
p
uyu
2
1
(6)
Equation (3) of the Poisson equation can now be reduced into the
Laplace’s equation by substituting Eq. (6) into Eq. (3) to write
0
2
2
2
2
w
w
w
w
y
u
x
u
pp
(7)
The boundary conditions for
p
u are newly written as
0
w
w
y
u
p
for 0 x
0
w
w
x
u
p
for 0 y
2
1 yu
p
for 1 x
0
p
u for 1 y
(8)
In Eq. (7) the boundary conditions (8) are the same as the heat conduc-
tion problem in a square plate, to which the analytical solution is possible
by solving the equation through the method of the separation of variables.
The solution for
p
u consists of particular product solutions in the form
yYxXyxu
p
,
(9)
Substituting Eq. (9) into Eq. (7) yields
337

6 Newtonian Flow
0
2
2
2
2
dy
Yd
XY
dx
Xd
(10)
and after separating the variables, we may be able to set the equation to the
flow
2
2
2
2
2
11
c
dy
Yd
Y
dx
Xd
X
(11)
where
2
c is the arbitrary constant. As a result, there follows a set of ordi-
nary differential equations
0
2
2
2
Xc
dx
Xd
(12)
0
2
2
2
Yc
dy
Yd
(13)
Equations (12) and (13) constitute a Sturm-Liouville problem through
which the characteristic values are given where
2
12
S
ncc
n
for ,3,2,1 n
(14)
It follows that the solution is written for a series of the form where
¦
f
1
coshcos
n
nnnp
xcycau
(15)
and
n
a satisfies Eq. (7) with the boundary conditions in (8). The final form
of
p
u is given as
¦
f
1
3
coshcos
cosh
1
4
n
nn
nn
n
p
xcyc
cc
u
(16)
It should be kept in mind that the actual solution of
u is expressed with
Eq. (6) by substituting
p
u in Eq. (16). In Fig. 6.17, the velocity profile is
schematically drawn by velocity contour, which is the same as the tem-
perature contour in the case of a heat conduction problem.
Note that Eq. (7) is a partial differential equation of the elliptic type.
The equation can be fairly easily solved by a numerical method, such as
338

Problems
the finite difference method. The reader may be worth trying to write a
program code to solve the problem. This is left to reader’s own discretion,
similar to the Problem in 6.4-5 (which is a type of parabolic partial differ-
ential equation).
Problems
6.4-1. Can the Poiseuille flow be used as a means of measuring the viscosi-
ties of liquids? Describe how and give a limitation for the method.
Ans.
>@
flowlaminar e within thYes,
6.4-2. In a horizontal circular pipe with a diameter of
m1010
3
u , a fluid
with a viscosity of sPa101
2
u
and density
33
mkg1021 u.
is
flowing. The discharge is
s
37
m1004
u. . Find the pressure drop in
a m10 section, and a maximum velocity in the pipe cross section.
Ans.
»
¼
º
«
¬
ª
u
su
p
m021
mN10631
max
26
.
.
6.4-3. Find the laminar flow velocity profile in a circular annulus for
bra dd . Assume that the pressure drop in a length l is p . The
fluid properties are such that the density is
U
and the viscosity is
0
K
,
which are kept constant. Also show that the maximum velocity oc-
curs at
^`
2
1
22
ln50 ababr . .
Ans.
»
¼
º
«
¬
ª
¿
¾
½
¯
®
'
2222
0
ln
ln
4
rb
ba
rb
ab
l
p
u
K
6.4-4. Prove Eq. (6.4.50).
6.4-5. Write a finite difference code for solving Eq (6.4.57).
Ans.
>@
2337SectionRefer ...
6.4-6. Show that the velocity profile of the laminar flow in a square duct is
equivalent to the temperature distribution of the heat conduction of
an identical square plate (without internal heat generation).
6.4-7. Verify that the volumetric flow rate
Q through a square duct is
given where
'
'
339

6 Newtonian Flow
»
»
¼
º
«
«
¬
ª
¿
¾
½
¯
®
¸
¹
·
¨
©
§
w
w
¦
f
1
5
4
0
tanh
61
3
4
n
n
n
c
c
a
z
p
Q
K
for a steady laminar flow of Newtonian fluid.
6.5 Laminar Boundary Layer Theory
The conceptual thought on the boundary layer is already given in the pre-
vious sections, for example, in the Problems 4.1-6, 4.1-8, and Section 6.3.3.
From a phenomenological point of view, the boundary layer is important to
flow, as in confined narrow regions near solid walls, where the effect of
viscosity comes into play. In addition, all the previous examples of the vis-
cous flow, in one way or another, have hinted strongly at boundary layer
behavior.
The idea about a boundary layer was first put forth by Prandtl (1904),
in his celebrated boundary layer equations, and a great deal of quantitative
information was also obtained in the exact solutions given by his student,
Blasius (1908). Von Kàrmàn (1921), suggested an integral method over the
thickness of the boundary layer, using a guessed velocity profile rather
than obtaining the exact solution of the equations. The excellent idea of
Kàrmàn’s leads to estimate the drag and wall shear of a viscous flow past a
flat plate at a high Reynolds number, and that is valid, in effect, for either
laminar or turbulent flow. The theory of the boundary layer carries particu-
lar importance in designing aircrafts, turbo blades in various turbo machin-
eries, and those are categorized as external flows. In this section, the thin
boundary layer approximations will be discussed. The boundary layer is
laminar at first and, as the Reynolds number increases, it undergoes a tran-
sition to turbulence. In order to convey the essence of the theory, the flows
that we discuss in this chapter are laminar, for which the Reynolds num-
bers are not too high. We will begin to study a two dimensional laminar
boundary layer flow in order to gain a fundamental insight within the
framework of the traditional approach.
6.5.1 Flow over a Flat Plate
Consider the laminar flow over a flat plate when the Reynolds number,
which we have yet to define, is high enough, before it undergoes a transi-
tion to turbulence. Here, we expect that the flow of an incompressible
340
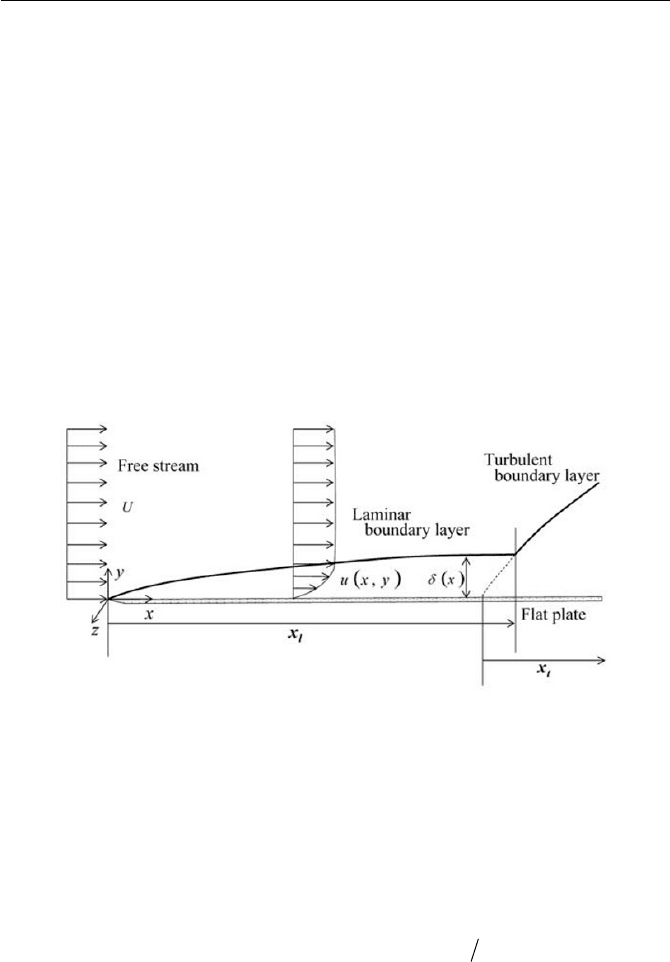
6.5 Laminar Boundary Layer Theory
stream velocity component, as indicated in Fig. 6.18. The flow in the con-
fined narrow region of high shear stress beginning from the leading edge
close to the plate, whose thickness is
x
G
, is two dimensional with veloc-
ity components,
0,,0,, vuuu
yx
u . The boundary layer thickness
x
G
is defined in such way that the height about the plate is Uu 990. ,
meaning that the streamwise velocity component u is within 1% of the
free stream velocity U , although u to U is asymptotic in direction. The
velocity boundary conditions of the boundary layer require no-slip and no
penetration at the wall of the flat plate, i.e.
00 ,xu
and
00 ,xv
for
0tx . Also, above the plate, outside the boundary layer the flow is treated
as the inviscid, i.e.
Uyxu , and
0, yxv for 0!x and
xy
G
!! .
In the boundary layer, more importantly inertial effects and viscous ef-
fects are both significant, so that it appears that we need to solve the Na-
vier-Stokes equation, whereas outside the boundary layer the Euler equa-
tion may be used. By focusing our attention within the boundary layer, we
may write the continuity equation and the Navier-Stokes equation, as the
starting point for a discussion on flat plate boundary layer flow. The non-
dimensionalized governing equations are given by taking the representa-
tive length scale as
x
, velocity as U , time scale as Ux and pressure scale
as
2
U
U
, as follows
Fig. 6.18 Boundary layer over a flat plate
341
Newtonian fluid with density
U
and viscosity
0
K
is planar, with no cross-

6 Newtonian Flow
1o1o
0
w
w
w
w
*
*
*
*
y
v
x
u
(6.5.1)
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
w
w
w
w
2
2
1
1
o1oo1o 1o1o
2
2
2
2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
G
G
y
u
x
u
Rex
p
y
u
v
x
u
u
t
u
x
(6.5.2)
¿
¾
½
¯
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
w
w
w
w
*
*****
*
*
*
*
*
*
*
*
*
*
*
*
*
*
G
GGGGG
1
oooooo
2
2
2
2
2
1
y
v
x
v
Rey
p
y
v
v
x
v
u
t
v
x
(6.5.3)
In applying Eqs. (6.5.1), (6.5.2) and (6.5.3) to the boundary layer, sub-
stantial simplification of these equations can be made by recalling that;
(i) the flow is predominantly parallel to the plate, i.e.
vu !!
(ii) the boundary layer thickness
x
G
is very thin, i.e.
xx
G
implying that axial derivatives of velocity components are much smaller
than the transverse derivatives of those same components, and that the
transverse pressure gradient is much smaller than the axial pressure gradi-
ent.
Using the conditions from (i) and (ii), we can perform an order-of-
magnitude analyses. In order to make the point clear in Eqs. (6.5.1), (6.5.2)
and (6.5.3), the order of each term is shown in the equations below, where
1o is determined such a way that, for example, 1| Uuu
*
and
1|
*
x
so that
1o|ww
**
xu , whereas
**
G
| Uvv and
**
G
G
| xy so that
1o|ww
**
yv
, and so on. Let
x
Re
denote the Reynolds number, defined
by
XUK
UxUx
Re
x
0
(6.5.4)
The important issue that arises for the viscous terms of
2
2
**
yu ww
and
2
2
**
yv ww
, for which as fo
x
Re and 0o
*
G
, the condition of Eqs.
(6.5.2) and (6.5.3) not being reached to the inviscid limit is that
342
6.5 Laminar Boundary Layer Theory
1o
1
2
2
|
w
w
u
*
*
y
u
Re
x
(6.5.5)
and Eq. (6.5.5) indicates that
x
Re has to have the order
2
1
*
G
|
x
Re
(6.5.6)
as already displayed below, each term in Eqs. (6.5.2) and (6.5.3). Eq.
(6.5.6) consequently shows the important fact that the boundary layer
thickness
x
G
becomes thicker toward downstream, along the axial direc-
tion followed by the relation
x
Re
x
|
G
(6.5.7)
The pressure is such that
1o|
*
p , and since in y direction the varia-
tion of
*
p is very small, i.e.
***
G
o|ww yp ,
*
p is in effect given by the
inviscid flow outside the boundary layer.
It is now desired to derive an expression for the boundary layer flow by
using the order-of-magnitude analysis, and as a result we obtain the set of
simplified equations in a dimensional form as follows
0
w
w
w
w
y
v
x
u
(6.5.8)
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
2
2
0
y
u
x
p
y
u
v
x
u
u
t
u
KU
(6.5.9)
y
p
w
w
0
(6.5.10)
and for the inviscid core flow
x
p
x
U
U
t
U
w
w
w
w
w
w
U
1
(6.5.11)
These are the so-called Prandtl’s boundary layer equation. The boundary
layer equations however, are still kept in nonlinear terms (as seen in Eq.
(6.5.9) in convective terms. Nevertheless, one of the important aspects of
the equations is that the pressure gradient in Eq. (6.5.9) may be determined
343
