Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


6 Newtonian Flow
Ans.
>@
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
|?
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¿
¾
½
¯
®
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
|
¿
¾
½
¯
®
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
|
f
f
f
f
f
³
³
³
f
f
f
306
306
2242
2
1
2
2
1
2
32
32
52
4
3
3
2
2
32
3
2
2
0
0
2
2
2
2
2
2
2
2
0
0
0
99
GU
99
G
G99GGG99GG
9GGGGG
G
GGG
U
G
GGG
U
G
G
G
G
G
G
TTUc
dx
d
q
dy
yyyyyy
dy
yyyy
TTUc
dx
d
dy
yyyy
TTUc
dx
d
q
wp
w
T
T
T
wp
T
T
wp
w
6.6 Turbulent Flow
Osborne Reynolds (1895) tried to give theoretical explanation for the em-
pirical criterion
2300d
X
Ud that rules out turbulent flow, observed in his
celebrated experimental apparatus, the Reynolds tank. He manipulated the
continuity and Navier-Stokes equations into a form that can predict the
time-averaged behavior of turbulence. When entering into the subject of
turbulent flow, it is essential to understand that, in most engineering appli-
cations, the kind of flows is shear flow. They can be bound by a solid wall
or they may be free, such as with boundary layers and pipe flows, or free
jets and wakes. In this section, greater emphasis is placed on the flow
characteristics of a mean flow from the act of turbulence, rather than on
turbulent motions and their associated structure. Moreover, we will com-
bine the subject into incompressible Newtonian flows for the sake of clear
understanding.
The nature of turbulent flow is three dimensional, at which velocity
and pressure at a certain point do not remain constant with time but per-
form highly irregular fluctuations, and mixing of fluid in a turbulent flow,
is much higher than in laminar flow, resulting in a more uniform mean of
velocity distribution in comparison to a laminar flow, owing to a mixed
dispersion of momentum. Also the intermittency is of notable phenomenon,
as observed in measuring a turbulent flow field, such as the velocity record
in relation to time variations. This phenomenon can occur when noticing
the Reynolds number is close to the transition between the laminar and the
turbulent flow in pipes and boundary layers.
Turbulent motions of fluid particles are so complex that they cannot be
treated individually, although they are deterministic and predictable in
6.5-5. Prove Eq. (5) in Exercise 6.5.2.
364
6.6 Turbulent Flow
principle from the mass and momentum equations, once an appropriate
boundary and initial conditions are given. In practice, because of the ap-
parent randomness of turbulent flows, we will take an averaging approach
to obtain the means of motion to enable us to discover a statistical flow de-
scription that includes turbulent properties. The average value of a flow
quantity f (such as
u or
p
) of a Eulerian flow description in turbulent
flows is obtained via an ensemble average that is defined by
»
¼
º
«
¬
ª
¦
fo
N
i
i
N
tf
N
tf
1
,
1
lim xx,
(6.6.1)
where all samples are drawn at the same time with the same position rela-
tive to the flow field boundaries. The ensemble average expressed in Eq.
(6.6.1) allows for the possibility of an unsteady mean flow. However, from
a practical point of view, data drawn from an ensemble average of nomi-
nally identical experiments is never available. Indeed, in turbulent flows,
most available quantitative information will be gained for flows that are
statistically stationary flows, the average of f given by the time average
that is defined as
³
Tt
t
dttf
T
tf
0
0
,
1
,
00
xx
(6.6.2)
where
0
x
is a point
0
xx
,
T
the averaging time and
0
t
the starting time.
Note that
0
t is not important. Nevertheless,
T
must be large enough so
that any further time elapsed has no significant effect on the measured
value of
f . For f in the statistically stationary flows, the ergodic hy-
pothesis is held such that the ensemble average of each flow variable is the
same as its time average in certain fairly general conditions.
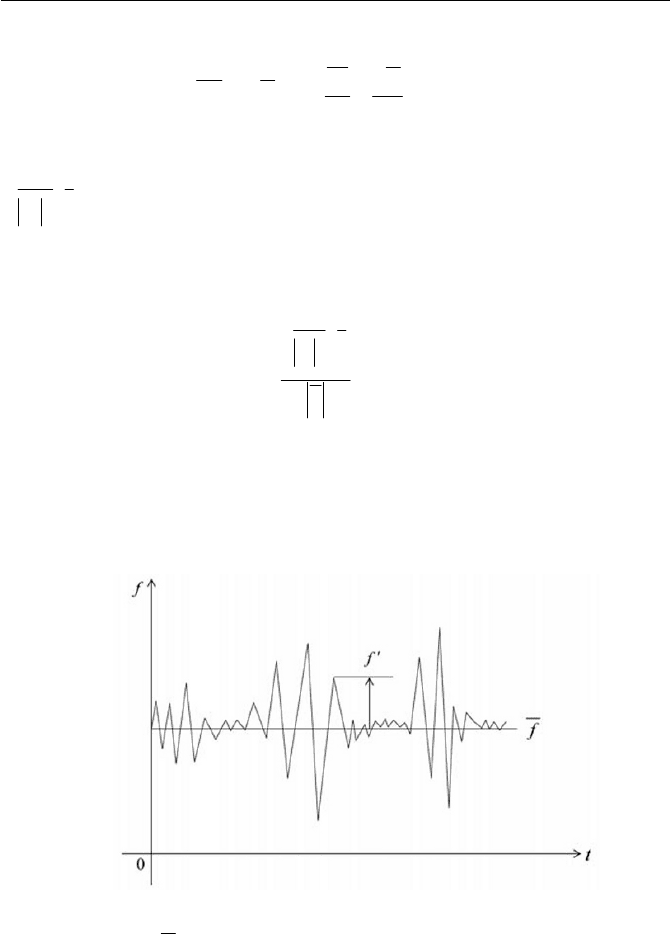
According to Reynolds, we decompose each flow variable f as a sum
of the mean value
f and the fluctuation f
c
from the mean. Thus,
tftftf ,,, xxx
c
(6.6.3)
and simply, as illustrated in Fig. 6.25, we can write
fff
c
(6.6.4)
It is clearly shown that
0
c
f and ff
(6.6.5)
365
6 Newtonian Flow
and that for the differential operation we have
ff and
t
f
t
f
w
w
w
w
(6.6.6)
It will prove useful to mention that the root mean square of f
c
, i.e.
2
1
2
¸
¹
·
¨
©
§
c
f is not zero, and in consideration of f as the instantaneous veloc-
ity
u in the turbulent flow field (i.e. u{f ), we can define the relative
turbulent intensity
I
as
u
u
2
1
2
¸
¹
·
¨
©
§
c
I
(6.6.7)
The turbulent intensity is often used for determining the level of turbulent
intensity. In a typical turbulent flow in an engineering application, the tur-
bulent intensity is approximately 10.I | . Note that the critical Reynolds
number at the transition depends upon
I
in the upstream.
Fig. 6.25 Superimposition of turbulent fluctuation
f
c
and the mean
value
f
Now we shall consider the mass and momentum conservation equa-
tions for an incompressible, isothermal, Newtonian fluid of density
U
and
viscosity
0
K
, respectively:
366
6.6 Turbulent Flow
0 u
(6.6.8)
and
uuu
u
2
0
¸
¹
·
¨
©
§
w
w
KUU
p
t
(6.6.9)
where the gravitational (body force) term is ignored. Decomposing
u
and
p
respectively where
uuu
c
(6.6.10)
ppp
c
(6.6.11)
and substituting into Eqs. (6.6.8) and (6.6.9) yields
0
c
uu
(6.6.12)
and
»
¼
º
«
¬
ª
cc
c
c
w
c
w
uuuuuuuu
uu
t
U
uu
c
c
2
0
K
pp
(6.6.13)
Taking the average of each term in Eqs. (6.6.12) and (6.6.13) as a result,
we can obtain
0 u
(6.6.14)
and
uuuuu
u
cc
w
w
UKUU
2
0
p
t
(6.6.15)
Equation (6.6.15) differs from the Navier-Stokes equation for the average
flow because of the extra term on the last term in the right hand side of the
equation. This quantity
uu
cc
U
R
IJ
(6.6.16)
is called the Reynolds stress, and Eq. (6.6.15) is called the Reynolds equa-
tion. The Reynolds stress
R
IJ acts on a control surface that moves with the
local averaging velocity
u , just as though a stress equals to
uun
cc
U
ˆ
.
367

6 Newtonian Flow
There is a closure problem in the Reynolds equation for the Reynolds
stress in Eq. (6.6.16), which has to be attained with an appropriate equa-
tion. In order to eliminate the closure problem and to obtain an appropriate
equation, we may be able to set a transport equation for
''uu , by setting
u
c
1366Eq. .. dyadic product of
u
c
to Eq. (6.6.13) then averaging
(6.6.17)
Equation (6.6.17), after some manipulation, however, generates a higher
order of terms, such a
uuu
ccc
, and consequently it requires another ef-
fort to give an equation for
uuu
ccc
, and so forth. This would require end-
less labor without knowing substantial information. In order to make the
problem easier, we need an independent equation for the Reynolds stress.
The independent equation for the nature of a constitutive equation or a so-
called turbulent model may be necessary.
It is appropriate to give a turbulent model analogous to a Newtonian
constitutive equation, by referring to Eq. (6.11), to the Reynolds stress
where
Ik
T
t
UKU
3
2
¸
¹
·
¨
©
§
cc
uuuu
(6.6.18)
or in tensor notation
ij
i
j
j
i
tji
k
x
u
x
u
uu
GUKU
3
2
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
cc
(6.6.19)
where
t
K
is defined as the eddy viscosity and k is the average kinetic en-
ergy of the turbulence per unit mass, which is defined as
22
2
1
2
1
2
1
jjii
uu
k
c
c
c
c
uu
(6.6.20)
It should be mentioned that the addition of the second term in Eq.
(6.6.18) or Eq. (6.6.19) is due to the result of defining
k
as expressed in Eq.
(6.6.20). From the definition of k in Eq. (6.6.20),
k is used as a charac-
teristic scale of velocity if no other velocity characterizes the turbulent
flow. Thus, it is appropriate to define the Reynolds number for the turbu-
lence as
368

6.6 Turbulent Flow
XUK
cc
t
lklk
Re
0
(6.6.21)
where
c
l is the characteristic length, which can also be chosen as the
length scale of the largest fluctuations, such as a diameter in a pipe flow.
It is necessary to estimate the scales of time and the length in a turbu-
lent flow for a consideration of the turbulence structure and a statistical de-
scription of the fluctuations. The important scales of length and time are
the Kolmogorov scales. The argument used to estimate those scales is
based on the idea that the kinetic energy is transferred down the energy
cascade to smaller and smaller length scales with an increased rate of de-
formation induced by the smallest eddies. There would be an end of energy
cascade where the length is sufficiently small enough for the energy to be
dissipated by a viscous action. The mean rate of dissipation energy per unit
of mass
H
is brought in the equilibrium region by larger eddies, where the
turbulence is assured to be locally isotropic. At the equilibrium region the
kinematic viscosity
U
K
X
0
is also an important parameter to control the
dynamics. Thus, at the equilibrium region, the length scale
k
O
and time
scale
k
W
for the smallest eddies, or the smallest fluctuations can be ob-
tained by combination of the dimensions
32
TL and TL
2
for
H
and
X
respectively, as
4
1
3
¸
¸
¹
·
¨
¨
©
§
H
X
O
k
and
2
1
¸
¹
·
¨
©
§
H
X
W
k
(6.6.22)
where
k
O
and
k
W
are called the Kolmogorov (or dissipation) scales of
length and time respectively. It may be speculated from energy accounting
that
H
is proportional to
c
lk
3
, so that in Eq. (6.6.22) we can write for
k
O
as
4
3
t
c
k
Re
l
|
O
(6.6.23)
It should be further considered that multiplication of
k
W
and k can
give an estimate of the average length scale of the fluctuations
T
O
, which
is called the Taylor microscale, which is given by
369

6 Newtonian Flow
2
1
t
c
T
Re
l
|
O
(6.6.24)
Thus, from Eqs. (6.6.23) and (6.6.24) we have reached an important rela-
tionship where
4
1
t
k
T
Re|
O
O
(6.6.25)
Namely, Eq. (6.6.25) shows that the average length scale of the fluctuation
of order is
4
1
t
Re times the Kolmogorov scale (the smallest scale).
6.6.1 Turbulence Models
There are numerous turbulence models, ranging from the simplest alge-
braic correlations to second-closure models by Wilcox (1998), which are
further extended to be based on CFD with large eddy simulations (LES)
and direct numerical simulations (DNS). In the proceeding sections, in
view of engineering applications, we shall look into the most basic models
of zero-equation models: one-equation models and two-equation models,
all of which deal with the eddy viscosity
t
K
and the average kinetic energy
of turbulence
k .
(i) Zero-equation model
In a two dimensional turbulent boundary layer flow of an incompressi-
ble fluid, denoting
0,,vu u and
0,,vu
c
c
c
u , we have the following set
of equations from Eqs. (6.6.14) and (6.6.15), such as
0
w
w
w
w
y
v
x
u
(6.6.26)
vu
y
y
u
x
p
vu
y
u
xt
u
cc
w
w
w
w
w
w
»
¼
º
«
¬
ª
w
w
¸
¹
·
¨
©
§
w
w
w
w
UKU
2
2
0
2
(6.6.27)
0
2
c
w
w
w
w
v
yy
p
U
(6.6.28)
For the inviscid flow from Euler equation, Eq. (6.5.11), we have
370
6.6 Turbulent Flow
x
p
x
U
U
t
U
w
w
w
w
w
w
U
1
(6.6.29)
In the momentum equation in Eq. (6.6.27), the third term in the right hand
side of the equation includes the turbulent shear stress
t
W
vu
t
cc
UW
(6.6.30)
The simplest way to give a constitutive relation to
t
W
is to introduce the
eddy viscosity
t
K
as analogous to the molecular shear viscosity with refer-
ence to either Eq. (6.6.18) or (6.6.19)
¸
¸
¹
·
¨
¨
©
§
w
w
y
u
tt
KW
(6.6.31)
It is noted that
t
K
is not a fluid property, but depending upon flow condi-
tions and thus varying with position,
t
K
is a positive value, and the gradi-
ent
yu ww is positive under typical boundary layer flows. For a positive
t
K
in Eq. (6.6.31), the shear correlation
vu
cc
must thus be negative, which
is supported by experimental observation.
One successful approach to estimate
t
K
is the mixing length concept of
Prandtl (1925). The basic idea is to assume that
u
c
and v
c
are each propor-
tional to
yu ww , i.e.
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
|
cc
y
u
l
y
u
lvu
21
UU
(6.6.32)
where
1
l and
2
l are mixing lengths.
1
l and
2
l represent a degree of aver-
age eddy size, and may be conveniently replaced by a representative length
l . Thus using l , Eq. (6.6.32) may be written as
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
cc
y
u
y
u
lvu
2
UU
(6.6.33)
Comparing Eq. (6.6.33) with Eq. (6.6.31), we can write
t
K
where
y
u
l
t
w
w
|
2
UK
(6.6.34)
371

6 Newtonian Flow
Thus the difficulty arises again to determine
l
, which is just replaced
in ignorance of
vu
cc
. However, if we can relate the mixing length l to the
flow condition, the model will be completely determined as a closed sys-
tem that deals with l . We will look into the turbulent boundary layer in
more detail by decomposing the turbulent flow over a flat plate for the
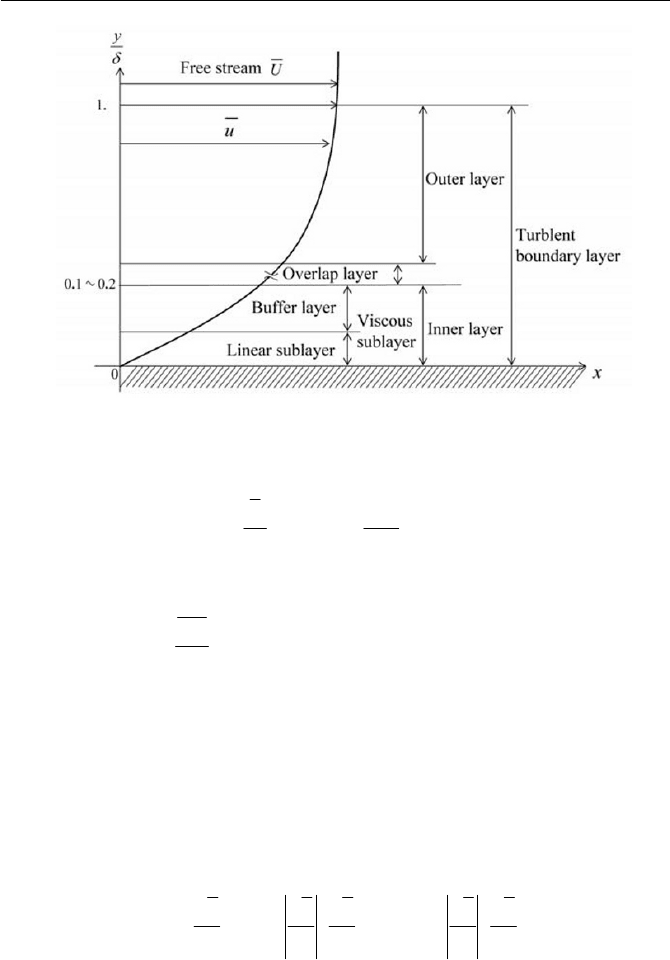
sake of clearness, as schematically shown in Fig. 6.26. As indicated in Fig.
6.26, the turbulent boundary layer is composed chiefly by two layers: one
is a thin inner layer close to the wall, where the viscous effects are signifi-
cant; another is a thicker outer layer where the viscous effect is insignifi-
cant. There is a region called an overlap layer in-between the inner and
outer layers, where the inertial and viscous effects are both insignificant. In
the free stream, viscous and Reynolds stresses do not play important roles.
As it is shown further in Fig. 6.26, from inside of the inner layer, there are
two distinct layers, and they are identified as buffer layers and linear sub-
layers. Those two layers are altogether called viscous sublayers, where vis-
cous effects are significant. In the linear sublayer, the Reynolds stress ef-
fects are insignificant, while in the buffer layer viscous and Reynolds
stress effects are comparable.
As to the mixing length l , the primary effect is the distance from the
wall. The following correlations were suggested by Prandtl and Kàrmàn
In the viscous sublayer:
2
yl |
(6.6.35)
In the overlap layer: ayl |
(6.6.36)
In the outer layer: constant|l
(6.6.37)
It will prove useful to nondimensionalize the quantity
vu
cc
by knowing the
parameters
U
,
X
, y and
w
W
in the boundary layer as follows
¸
¹
·
¨
©
§
cc
X
W
W
yu
g
u
vu
2
and
¸
¹
·
¨
©
§
X
W
W
yu
f
u
u
(6.6.38)
where we define the velocity
W
u , the so-called friction velocity which is
given as
U
W
W
w
u
(6.6.39)
372
6.6 Turbulent Flow
Fig. 6.26 Structure of turbulent boundary layer over a flat plate
Using conventional notations for these nondimensional parameters
W
u
u
u
and
X
W
yu
y
(6.6.40)
we can write Eq. (6.6.38) simply by
cc
yg
u
vu
2
W
and
yfu
(6.6.41)
The correlational expression of Eq. (6.6.41) is called the law of the
wall. From the argument of the law of the wall, we can readily calculate
the velocity profile in the overlapping layer for hydrodynamically smooth
flat plates with a zero attack angle and a zero pressure gradient (the total
shear stress is constant near the wall), assuming that the turbulent (shear)
stress
t
W
is written as the eddy viscosity
t
K
(with reference to Eq. (6.6.34))
and the mixing length
l (with reference to Eq. (6.6.36)) as follows
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
y
u
y
u
ya
y
u
y
u
l
y
u
tt
222
0
UUKKW
(6.6.42)
Via the assumption of
0
K
K
!!
t
in the overlap layer, we can relate the ve-
locity profile
W
u
with a shear stress, using Eq. (6.6.39), in the following
manner
373
