Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

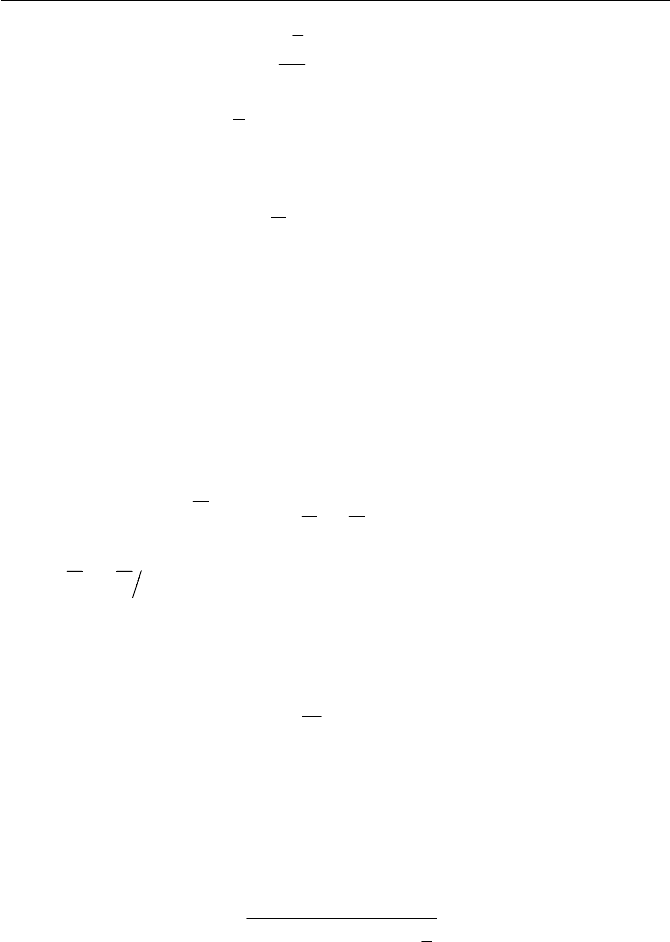
6 Newtonian Flow

2

22

W

UU

u

y

u

ya

¸

¹

·

¨

©

§

w

(6.6.43)

Solving Eq. (6.6.43) for

u and using the notation from Eq. (6.6.41), we

can obtain a correlation of







yf as



by

a

u 



ln

1

(6.6.44)

The expression is called the logarithmic velocity distribution, where a and

b

are suggested, for example, by Coles and Hirst (1968) as

41.0|a and 0.5|b

With these constants, Eq. (6.6.44) gives good estimate for

35035 dd



y with ordinary flow conditions. Analogous to Eq. (6.6.44),

the correlation may be extended to the outer layer via the relationship

where

c

y

a

uU 

¸

¹

·

¨

©

§

 



G

ln

1

(6.6.45)

where

W

uUU



and c are constant depending upon the pressure gradi-

ent, and often upon flow parameters. In order to cover the correlation be-

tween the viscous sublayers, the following expression by van Driest (1956),

is helpful

D

A

y

ayeayl

D

»

¼

º

«

¬

ª

|

¸

¹

·

¨

©

§





1

(6.6.46)

where

D

is the damping factor and A is the configuration parameter.

Adopting Eq. (6.6.46), the velocity profile may be given in the following

form, similar to Eq. (6.6.44), as follows





³





y

D

ya

dy

u

0

2

1

2

411

2

D

(6.6.47)

It is noted that

26 A

is given to a case of flow over a flat plate.

In the most adjacent layer to the wall, where the viscous effect domi-

nates the flow, i.e.

t

K

!!

0

, we may write the turbulent shear stress as

374

6.6 Turbulent Flow



2

00

W

UKKKW

u

y

u

y

u

tt

¸

¹

·

¨

©

§

w

|

¸

¹

·

¨

©

§

w



(6.6.48)

which gives a simple differential equation for



u

e

y

u

w



(6.6.49)

and thus with a boundary condition, i.e. 0



u for 0



y , we have



ycu

0

(6.6.50)

where

0

c is a constant. Equation (6.6.50) gives a linear velocity profile in

the linear sublayer. The range of Eq. (6.6.50) is valid within approximately

5030

~d



y (the buffer layer)

(ii) One-equation model

This is a model to unite an equation for k given in Eq. (6.6.20), and

the momentum equation in Eq. (6.6.15) which is solved in coupled with

the continuity equation of Eq. (6.6.14).

We shall now write a transport equation for

k , by starting to obtain a

mechanical energy equation, multiplying (dyadic product of)

u

(or

i

u ) to

the Navier-Stokes equation where

»

¼

º

«

¬

ª

w



w



¸

¹

·

¨

©

§

w



w

2

0

j

i

j

i

j

i

x

u

x

p

u

x

u

t

u

KU

(6.6.51)

which directly gives

j

i

j

i

j

i

j

jj

i

ii

x

u

x

u

x

u

x

u

x

u

x

uu

p

u

x

uu

t

w

¸

¹

·

¨

©

§

w



w



°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§

w



w



¿

¾

½

¯

®



¸

¹

·

¨

©

§



w



¸

¹

·

¨

©

§

w

XX

U

22

(6.6.52)

Now we will write Eq. (6.6.52) in terms of average and fluctuating quanti-

ties, substituting the following relationship in Eq. (6.6.52)

i

uuu

c



(6.6.53)

375

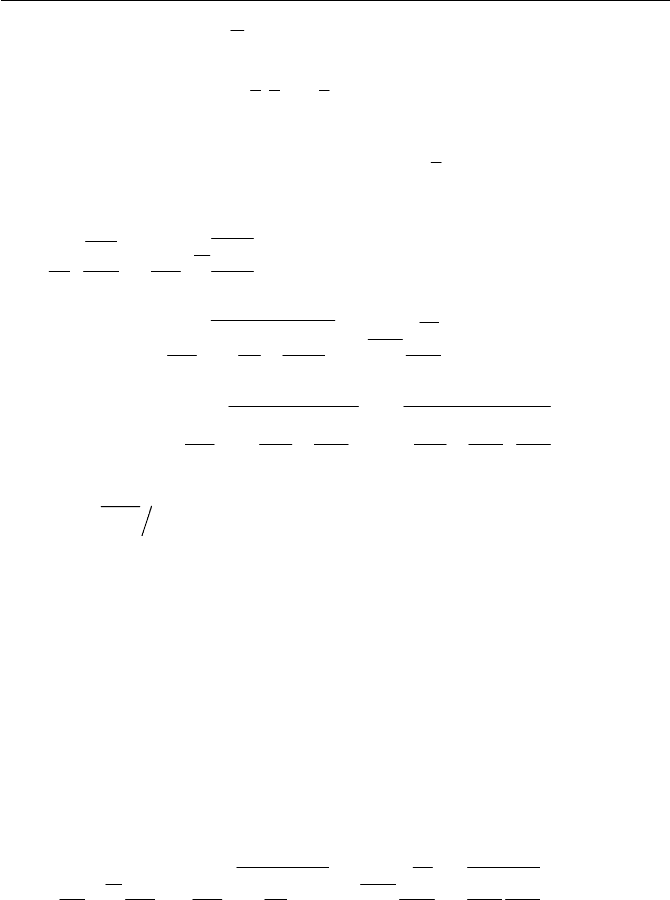
6 Newtonian Flow

ppp

c



(6.6.54)

iii

ii

uuuuuuuu

cc



c

 2

(6.6.55)

and taking the time average of both sides. Then we subtract with the Rey-

nolds equation in Eq. (6.6.15) after multiplying

i

u to it, and resultantly we

obtain

i

j

i

j

i

j

i

j

i

j

ji

jj

i

jj

i

ii

x

u

x

u

x

u

x

u

x

u

x

u

uu

p

u

x

uu

u

x

uu

t

w

c

w

¸

¹

·

¨

©

§

w

c

w



w

c

w



°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§

w

c

w



w

c

w

c

w



w

cc



°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§

cc



c

w



¸

¹

·

¨

©

§

cc

w



¸

¹

·

¨

©

§

cc

w

XX

U

2

22

(6.6.56)

where

2

jj

uuk

cc

. Each term of Eq. (6.6.56) contains identifiable energy

as counting from the 1st term on the left hand side of the equation to right

and over to the right hand side of the equation:

1.

time rate of change of k

2.

convection of k by means of the mean flow

3.

convection of total energy by means of turbulence

4.

production of turbulence taken from the mean flow

5. work done by viscous effect due to turbulence motion

6.

dissipation of turbulence by turbulence motion

Equation (6.6.56) seems formidable, but the introduction of the pa-

rameter leads to a lose of novel algebraic difficulties and as a result it will

be written in the boundary layer form, with a non-conservation form, as

follows

i

j

i

j

i

j

jii

ii

i

x

u

x

u

x

u

uuk

p

u

xx

k

u

t

k

w

c

w

c

w



w

cc



°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§



c

w



w



w

X

U

(6.6.57)

In one equation model, the three terms appearing on the right hand side

of Eq. (6.6.57) are replaced by each appropriate term. Typically, in the first

term, the convection of total energy can be replaced by a gradient diffusion,

such that

376

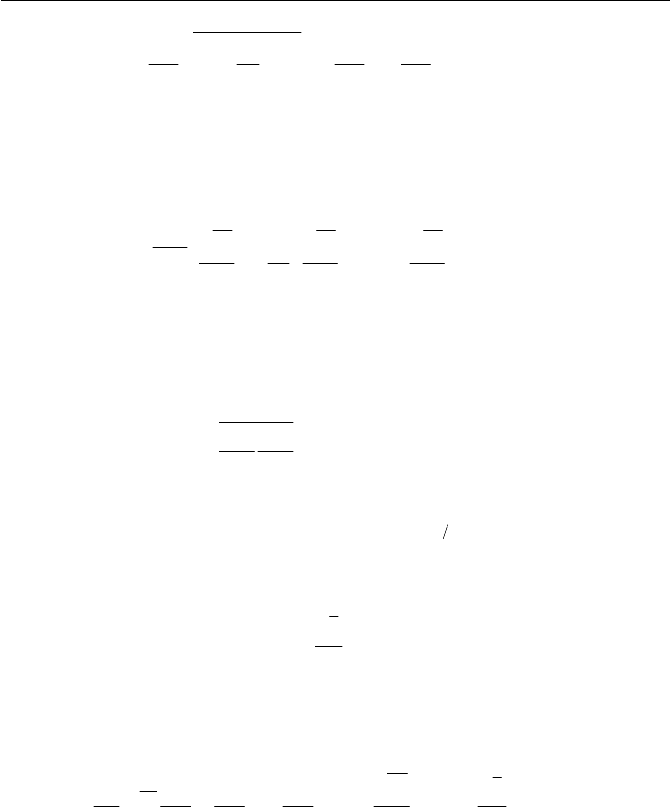
6.6 Turbulent Flow

¸

¹

·

¨

©

§

w

|

°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§



c



w

ii

i

x

k

x

k

p

u

x

1

D

U

(6.6.58)

where, by analogy with turbulent shear stress,

1

D

is a constant. The second

term, the production of turbulence, has already been modeled by the eddy

viscosity

t

K

in Eq. (6.6.30), so that

22

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w

cc



i

j

t

i

j

t

i

j

ji

x

u

x

u

x

u

uu

X

U

K

(6.6.59)

The third term, the dissipation of turbulence, is a difficult term to tackle as

its stands. The term, setting

H

, carries units of power per mass or



3

velocity per length, so that dimensionally it is convenient to relate

H

by

nm

i

j

i

j

lk

x

u

x

u

v

w

c

w

c

w

HX

(6.6.60)

where

k is the average kinetic energy of turbulence and l is a length scale

of an eddy moving with the velocity scale



21

k . Therefore, using Eq.

(6.6.60),

H

may be written as

l

k

2

3

2

DH

(6.6.61)

where

2

D

is a constant. Using Eqs. (6.6.58), (6.6.59) and (6.6.61) we can

write the energy equation, the so-called

k -equation, as follows

l

k

x

u

x

k

xx

k

u

t

k

i

j

t

iii

i

2

3

2

1

DXD



¸

¹

·

¨

©

§

w



¸

¹

·

¨

©

§

w



w

(6.6.62)

However, it should be kept in mind that Eq. (6.6.62) is not yet in closed

form since

l has not been correlated for with flow properties. For given

1

D

and

2

D

, “

l

” may be correlated by experimental verification by Kline

et al. (1968). One needs so much effort to solve Eq. (6.6.62), together with

finding a correlation for

l , and so far, one-equation model represented by

Eq. (6.6.62) is not popular, except for one particular problem.

377

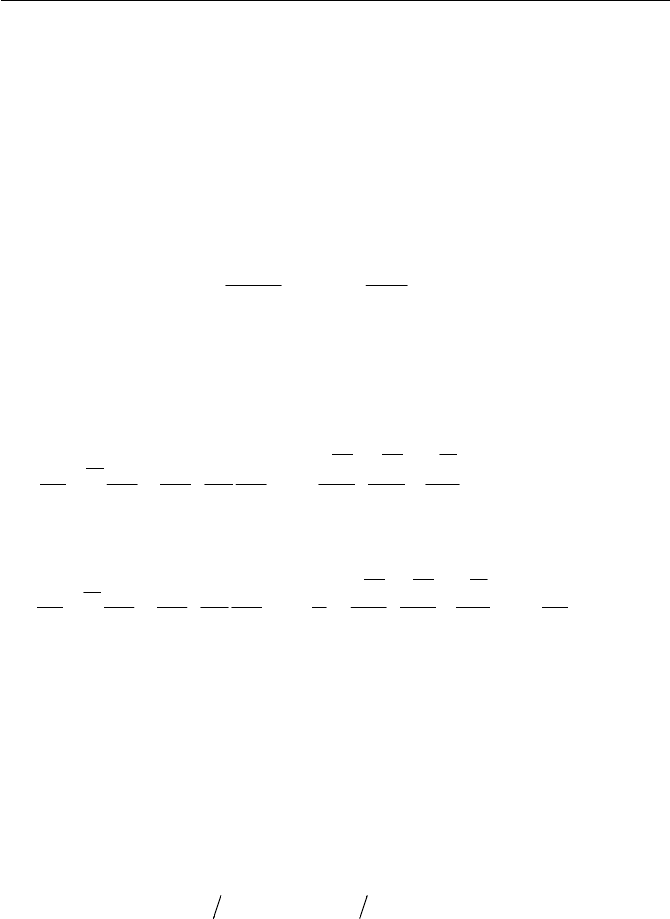
6 Newtonian Flow

As we see in one equation model, the difficulty is to determine the

characteristic length

l

, or alternatively, to determine

H

in the equation-k

given in Eq. (6.6.62). The two-equation model is generally based on an

idea that the characteristic length can be obtained by writing an additional

equation for the

k -equation. Among the most popular of the two-equation

model is the

k

–

H

model. With the

k

–

H

model, the eddy viscosity

t

K

is

further written with

k and

H

as

H

U

K

2

kc

t

"

(or

H

X

2

kc

t

"

)

(6.6.63)

where

"

c is a constant to be determined by experimental observation.

Similar to the one-equation model in Eq. (6.6.62), a set of

k –

H

equa-

tions is written by Tennekes and Lumley (1972) as follows:

k

-equation:

HX

V

X



¸

¹

·

¨

©

§

w



w



¸

¹

·

¨

©

§

w

|

w



w

j

i

j

i

j

t

ik

t

ii

i

x

u

x

u

x

u

x

k

xx

k

u

t

k

(6.6.64)

H

-equation:

k

c

x

u

x

u

x

u

k

c

xxx

u

t

j

i

j

i

j

t

i

t

ii

i

2

21

H

X

HH

V

XHH

H



¸

¹

·

¨

©

§

w



w



¸

¹

·

¨

©

§

w

|

w



w

(6.6.65)

There are five empirical constants appearing in

k

–

H

equations. The

k

–

H

model is widely used for analysis of two dimensional turbulent shear flows

at high Reynolds numbers. The five empirical constants were obtained via

experiments and are recommended for calculations:

441

1

. c , 921

2

. c , 090.

"

c , 01.

k

V

and 31.

H

V

(6.6.66)

Note that they are not universal constants, but can be modified for specific

problems. The constants given in (6.6.66) give good estimate for turbulent

flow characteristic for a flat plate with high Reynolds numbers. It is further

mentioned that

ktk

X

V

and

HH

X

V

t

are effective Prandtl numbers

defined by the eddy diffusivity.

In practical engineering applications the

k –

H

equations, Eqs. (6.6.64)

and (6.6.65), are solved with the continuity and momentum equations

where, respectively, Eqs. (6.6.14) and (6.6.15) are attained by numerical

methods. However, the models (the

k –

H

model) are designated to the

fully turbulent region away from solid walls. In the near region of solid

walls, due to strong viscous effects, the velocity gradient is very high, so

(iii) Two-equation model

378

6.6 Turbulent Flow

that in practical computations, there are needs for a large number of mesh

points to give sufficient resolutions. Even with modern super computers,

the number of mesh to gain sufficient resolution for turbulence motion is

not enough. There could be some methods to overcome the problem. One

of the most fundamental methods is to use a wall-function to give an esti-

mate of turbulent properties at the first node point in a computational mesh

in the overlapping layers; with that, the calculation in the lower layer close

to the wall will not be necessary. In the region of the overlapping layer,

35035

dd



y , the turbulence energy production and dissipation is bal-

anced so that other terms beside the production and dissipation are unim-

portant. In this region, some significant use is expressed by virtue of the

logarithmic velocity distribution in Eq. (6.6.44), which gives a first esti-

mate for the

k –

H

parameters for the closest node



py to the wall, as

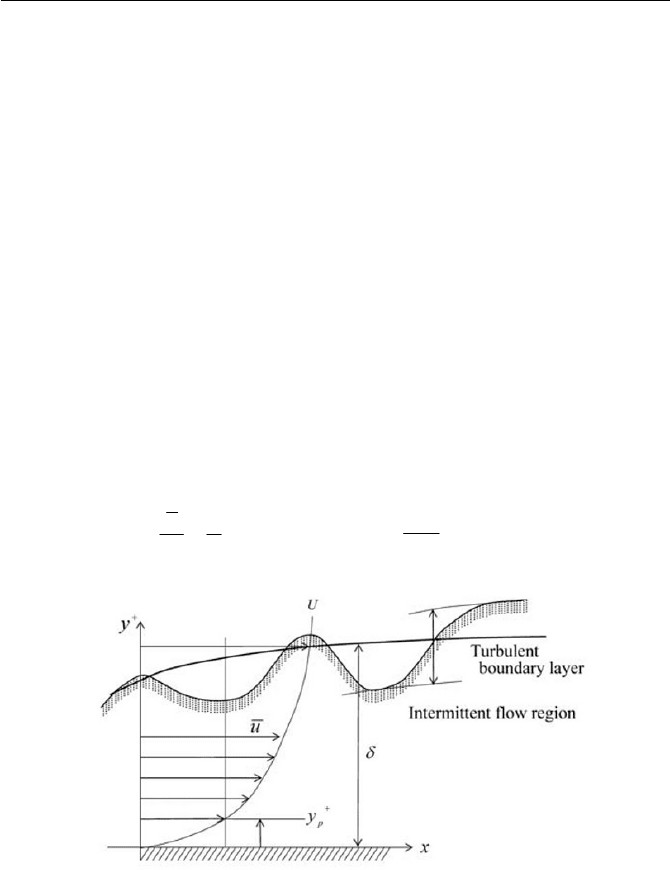
schematically displayed in Fig. 6.27. Then the

k –

H

equations are solved

to give converged solutions by a numerical procedure. According to the

idea close to the wall,



p

uu

will be then given via



p

y

using the wall-

function as



By

au

u

p



ln

1

W

,and

X

W

yu

y

p



(6.6.67)

Fig. 6.27 Node point



p

y

with wall-function

where

410. a

and

77.7 B

. In order to examine

k

close to the wall, the

k -equation in the two dimensional turbulent boundary layer in the over-

lapping layer is considered to be

379

6 Newtonian Flow

0 

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w

UHK

y

u

y

u

t

(6.6.68)

It is further known that the shear stress





yu

t

ww

K

is nearly equal to the wall

of shear stress

2

W

UW

u

w

, so that we can write

2

W

UWK

u

y

u

wt

|

¸

¹

·

¨

©

§

w

(6.6.69)

Using the expression in Eq. (6.6.63) for

t

K

, we can calculate k where

2

1

2

l

c

u

k

W

(6.6.70)

Thus,

k is determined by

W

u with Eq. (6.6.70). Similarly, for

H

in Eq.

(6.6.68), we can obtain

2

¸

¹

·

¨

©

§

w

y

u

t

U

K

H

(6.6.71)

Using Eqs. (6.6.67) and (6.6.69),

H

is further written where

ky

u

3

W

H

(6.6.72)

Therefore, when

W

u is given a priori as a guessed value,

k

and

H

at



p

y

will be estimated. It is mentioned that

W

u is a quantity entirely determined

by a whole turbulent flow field calculation, provided that only

W

u is finally

determined at the end of recurrence procedure in a numerical calculation.

It is also useful to give

u and

W

u

a relationship, which is given in Eq.

(6.6.67) as

¸

¹

·

¨

©

§

X

W

2

1

4

1

2

1

4

1

2

ln

1 kc

yB

a

kc

u

l

p

l

(6.6.73)

for

p

y at



p

y ,we set

X

21

41

kcyy

l

pp



.

380

6.6 Turbulent Flow

6.6.2 Turbulent Heat Transfer

In a non-isotropic temperature field, it becomes necessary to take into ac-

count the energy equation in addition to the continuity and momentum



equations in turbulent flows. Particularly, in a compressible flow there ap-

pears a strong interaction between the velocity and temperature field. The

general treatment for a turbulent heat transfer is far from complete, and

rather it is at the developing stage in the research of turbulent flows. In this

section of the chapter, we shall look into the characterization of turbulent

equation in turbulent boundary layers, using the Reynolds’ analogy as ex-

amined earlier (in Exercise 6.5.2).

The energy equation given with Eq. (2.5.29) can be written for an in-

force term, as follows



ee  

w

0

2

KU

U

TkTc

t

Tc

cp

p

u

(6.6.74)

where

e is the rate of strain tensor given in either Eq. (1.1.19) or (6.1.2).

For a turbulent flow, likewise, what we had done to the velocity, tempera-

ture

T

is also decomposed into its average part

T

and its fluctuating part

T

c

, where

T

c



(6.6.75)

Substituting Eq. (6.6.75), together with the velocity of Eq. (6.6.10) to Eq.

(6.6.74), and taking the average from the equation, we have

With a non-conservation form with tensor notation, we can write



2

0

2

°

¿

°

¾

½

°

¯

°

®



¸

¹

·

¨

©

§

w

c

w



w

c

w



¸

¹

·

¨

©

§

w



w



cc

w



¸

¹

·

¨

©

§

w

i

j

i

j

i

ip

ii

c

i

p

x

u

x

u

x

u

x

u

Tuc

xx

T

k

xDt

TD

c

K

UU

(6.6.77)

In order not to lose the generality and to convey the essence of the sub-

ject, it appears that Eq. (6.6.76) can be written in a two dimensional

boundary layer over a flat plate:

heat transfer in two dimensional consideration of the averaged energy

compressible Newtonian fluid in the conservation form, ignoring the body





2

0

2 ee

c



cc



w

KUU

U

TkTcTc

t

Tc

c

pp

p

uu

(6.6.76)

381

6 Newtonian Flow

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w



w



w



¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w



w



w

y

u

y

u

y

u

y

q

y

T

k

yy

T

v

x

T

u

t

T

c

t

y

cp

KKU

0

(6.6.78)

where

y

q is defined as the turbulent heat flux against the molecular heat

flux (laminar heat flux) given by the term





yTky

c

wwww where

Tvcq

py

cc



U

(6.6.79)

It has been mentioned that





yu

t

ww

K

in Eq. (6.6.78) is introduced analo-

gous to the turbulent shear stress expressed in Eq. (6.6.31). It is further

postulated that in order to render Eq. (6.6.78) to make an amenable practi-

cal calculation that

y

q may be set, in analogous to the Fourier’s law in

laminar flow case, where

¸

¹

·

¨

©

§

w



y

T

Acq

tpy

(6.6.80)

where

t

A is the turbulent heat flux coefficient. Consequently, Eq. (6.6.78)

can be written as



2

0

¸

¹

·

¨

©

§

w



»

¼

º

«

¬

ª

w



w

¸

¹

·

¨

©

§

w



w



w

y

u

y

T

Ack

yy

T

v

x

T

u

t

T

c

ttpcp

KKU

(6.6.81)

The complete derivation of the energy equation of a turbulent heat transfer

is given first by Schlichting (1955).

The turbulent energy equation expressed in Eq. (6.6.81) is solved by

combining the continuity equation in Eq. (6.6.26) with the appropriate

momentum equations, for example, k –

H

equations for Eqs. (6.6.64) and

(6.6.65).

However, the problem arose where there exists another unknown quan-

tity

t

A in Eq. (6.6.81) that must be determined by the flow and thermal

variables. Considering the temperature field in heat transfer situation, there

exists an intimate connection between heat and momentum transfer in gen-

eral. Owing to this fact, we can extent the Reynolds’ analogy to the turbu-

lent heat transfer. In order to formulate the idea we can relate the eddy vis-

cosity

t

K

(the momentum exchange coefficient) and the turbulent heat flux

coefficient

t

A (the heat exchange coefficient), with the reason that both of

which have the common dimension of the molecular viscosity. A new non-

dimensional number, so-called the turbulent Prandtl number

t

Pr is analo-

382

6.6 Turbulent Flow

gous to the molecular Prandtl number





cp

kcPr /

0

K

, is a convenient pa-

rameter to relate the quantities

t

A

Pr

K

(6.6.82)

While we have the relationship of

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w



¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

w



y

u

y

T

Pr

c

y

u

y

T

Ac

q

t

p

t

tp

t

y

K

W

(6.6.83)

We are be able to collect the molecular heat conduction

c

q and the turbu-

lent heat transfer

t

q

terms in a kind of total rate of heat transfer q where

¸

¹

·

¨

©

§

w

¸

¹

·

¨

©

§

 

y

T

PrPr

cqqq

t

ptc

KK

0

(6.6.84)

yT ww / is taken as the positive gradient.

The analogy between the heat and momentum transfer in a flow over a

flat plate with a zero attack angle is discussed here in succession for the

laminar boundary layer case. With reference to Fig. 6.28, consider the lin-

ear sublayer in the turbulent boundary layer with Reynolds’ analogy, in

particular, where the momentum and heat transfer exchange (with coeffi-

cients respectively with

t

K

and

t

A

) are thought to be insignificant. There-

fore, it may not be far from reality to write the relationship between (Exer-

cise 6.5.2, Eq. (14)) , assuming that 1

|

t

Pr ,where

w

c

w

du

dTkq

¸

¹

·

¨

©

§



0

KW

(6.6.85)

On the other hand, with the turbulent outer layer as indicated in Fig.

6.28, the molecular coefficients of

0

K

and

c

k can be neglected, where it is

assumed that 1

|

t

Pr , so that Eq. (6.6.83) will become

¸

¹

·

¨

©

§



ud

Td

c

q

p

t

y

W

(6.6.86)

383

Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.