Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


6 Newtonian Flow
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
222
2
2
2
2
22
1
11
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
x
v
y
u
y
v
x
u
Ec
Re
y
T
x
T
PrRe
y
T
v
x
T
u
t
T
x
x
(6.5.41)
Then we carry out the order-of-magnitude analysis, similar to the
Prandtl boundary layer equations, discarding the terms
2
ww xu and
,
2
2 **
xT ww where we have the energy equation for the thermal boundary
in resultant dimensional form
2
0
2
2
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
y
u
y
T
k
y
T
v
x
T
u
t
T
c
cp
KU
(6.5.42)
The boundary conditions are, with the aid of Fig. 6.23, given as
txTtxT
txTtxT
w
,,,
,,0,
f
f
(6.5.43)
For the initial and inlet conditions, respectively
given,,
given0,,
0
{
{
tyxT
yxT
(6.5.44)
Equation (6.5.42) is also written in terms of thermodynamic properties and
the shear stress in the conservation form as
xy
uq
yy
vh
x
uh
t
h
W
UUU
w
w
w
w
w
w
w
w
000
(6.5.45)
where
2
2
0
uTch
p
is the total enthalpy of the flow. Neglecting the ki-
netic energy of
2
2
u , since 2
2
uTc
p
!! , the integral form of Eq. (6.5.45)
is thus, for the wall heat transfer
w
q
, written as
ff
f
f
f
¿
¾
½
¯
®
w
w
¸
¹
·
¨
©
§
w
w
³³
00
0
00
0
xyp
p
w
uTvcdyhhu
x
Tdyc
t
q
WUUU
354
Exercise
¿
¾
½
¯
®
w
w
¸
¹
·
¨
©
§
w
w
|
³³
f
f
f
0
00
0
dyhhu
x
Tdyc
t
p
UU
(6.5.46)
Furthermore, for the steady flow, i.e.
0 ww t
, we can write the heat trans-
fer quantity
w
q as
»
¼
º
«
¬
ª
¿
¾
½
¯
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
³
f
f
0
22
2
1
2
1
dyUhuhu
dx
d
q
w
U
(6.5.47)
where at the flat plate wall,
0
ww
y
c
w
yTkq . It should be kept in mind
that Eq. (6.5.47) is usually valid for a low speed laminar flow or a turbu-
lent boundary layer, customarily neglecting kinetic energy of
2
2
u
and
2
2
U (as
Ec
<<1). Thus the energy integral relation in the thermal bound-
ary layer, we can write
¿
¾
½
¯
®
³
f
f
0
dyTTuc
dx
d
q
pw
U
(6.5.48)
From Eq. (6.5.48) it is useful to derive an expression for the wall heat
transfer by defining the enthalpy thickness
h
G
defined as
³
f
f
f
¸
¸
¹
·
¨
¨
©
§
0
dy
U
u
TT
TT
w
h
G
(6.5.49)
so that we have
f
f
w
w
y
c
h
wpw
y
T
k
dx
d
TTUcq
G
U
(6.5.50)
where the thermophysical properties,
U
,
p
c ,
0
K
and
c
k are assumed to be
kept constant throughout the flow and thermal boundary layer.
Exercise
Exercise 6.5.1 Estimation of Drag Coefficient on Flat Plate
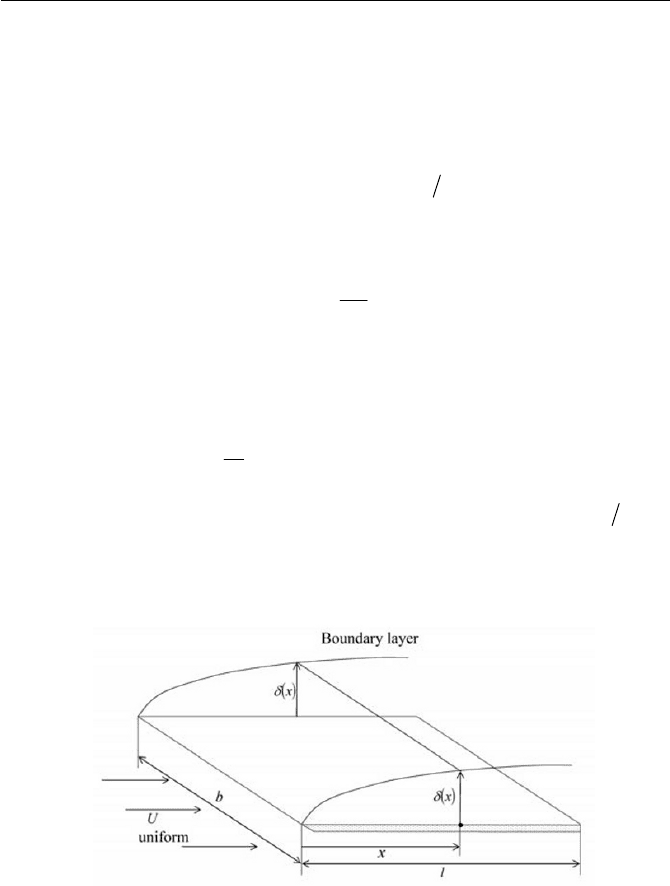
Consider a flat plate with a zero attack angle and obtain the drag force on
one side of the surface with a width of b and a length of l , assuming that
355
6 Newtonian Flow
the flow is isothermal, incompressible and in a steady laminar flow. The
fundamental geometrical configuration is shown in Fig. 6.24.
Ans.
For a flat plate with a zero attack angle, the condition for an inviscid
core flow parallel to the plate is given as
0 dxdU
, so that from the
Kàrmàn integral equation, the local wall sheer stress
w
W
is expressed in Eq.
(6.5.38) to be written as
dx
d
Ux
w
T
UW
2
(1)
where
T
is the momentum thickness and is a function of
x
.
T
can be de-
termined if the velocity profile in the boundary layer is known. We will
exploit a similarity solution of the velocity profile
KK
ff
U
u
n
(2)
where
K
is the y-directional distance from the wall defined by
xy
G
K
,
and
x
G
is the boundary layer thickness.
T
and
w
W
, thus, will be ex-
pressed in terms of
K
as follows
Fig. 6.24 Flow over a flat plate
G
KGT
1
1
00
2
1
c
dffdyuUuU
³³
f
(3)
356
Exercise
G
K
KG
KKW
K
U
c
UuU
y
u
y
w
0
2
0
0
0
0
»
¼
º
«
¬
ª
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
(4)
where
³
1
0
1
1
K
dffc and
0
2
fc
c
. Substituting Eqs. (3) and (4) into
Eq. (1), we have a new equation
Uc
c
dx
d
XG
G
¸
¹
·
¨
©
§
1
2
(5)
and is solved for
G
where
U
x
c
c
X
G
¸
¸
¹
·
¨
¨
©
§
1
2
2
(6)
Therefore, if the displacement thickness
G
c
is defined, such that
G
G
3
c
c
(7)
where
³
1
0
3
1
K
dfc , we have
U
x
c
c
c
X
G
¸
¹
·
¨
©
§
c
1
2
3
2
(8)
and for
T
, similarly
U
x
c
c
c
X
T
¸
¹
·
¨
©
§
1
2
1
2
(9)
The required drag force
D
F
on one side of the flat plate is thus calcu-
lated as
32
21
0
2
0
2 lUccb
dbU
dxbF
l
l
wD
XU
TU
W
³
³
357

6 Newtonian Flow
322
21
2 lUbcc
XU
(10)
and the drag coefficient
f
c is expressed by definition to be written as
2
1
21
21
2
22
22
2
1
¸
¹
·
¨
©
§
l
D
f
Recc
Ul
cc
Ubl
F
c
X
U
(11)
It is therefore mentioned that
D
F and
f
c are obtained by simply calculat-
ing
1
c and
2
c by giving the velocity distribution function
K
f .
In order to calculate Eqs. (10) and (11), we will take an approach of
guessing
K
f in the first place. Let us assume that
K
f is the polynomial
function of the 4th order, where
4
4
3
3
2
210
KDKDKDKDDK
f
(12)
where constants
40
D
D
~ are determined from the following physical con-
ditions of the boundary layer.
(i) 0 u so that
00 f for 0 y
(ii)
dx
dU
U
dx
dp
y
u
w
w
U
X
1
2
2
so that
00
cc
f for 0 y
(iii)
Uu so that
11 f for
G
y
(iv)
0
w
w
y
u
so that
01
c
f for
G
y
(v)
0
2
2
w
w
y
u
so that
01
cc
f for
G
y
It is noted that for 0 y , there is no-slip condition on the wall, i.e. 0
Q
and 0 u , so that
Q
does not appear in the conditions (i) ~ (v). By apply-
ing the conditions (i) ~ (v) to Eq. (12), we can obtain the constants
1and2020
43210
D
D
D
D
D
,,,
that give the velocity distribution function f as
43
22
KKKK
f
(13)
Thus, the drag force
D
F and the drag coefficient
f
c are given, according
358

Exercise
to Eqs. (10) and (11) and calculating
1
c and
2
c from Eqs. (3) and (4), by
322
68540 lUbF
D
XU
.
(14)
and
2
1
3711
lf
Rec .
(15)
Note that from the Blasius’ analytical solution,
f
c is given where
2
1
3281
lf
Rec .
(16)
The difference between Eqs. (15) and (16) is small, showing that the ap-
proach taken for the von Kàrmàn integral equation by adopting a guess-
velocity profile is correct.
f
c
in Eq. (15) or (16) is valid for
53
10510 udd
l
Re , as long as the boundary layer is thin enough (
G
<<
x
).
The method of the guess-velocity for the Kàrmàn integral equation is also
used for turbulent flows, by giving an appropriate turbulent velocity profile
in the boundary layer.
Exercise 6.5.2 Heat Transfer from a Flat Plate
Assume the profile of thermal boundary layer with reference to Fig. 6.23 is
given by a following second order polynomial function, similar to a second
order polynomial function guessed by velocity profile (see Problem 6.5-1),
such that
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
ff
2
21
TT
w
yy
TTTT
GG
(1)
Estimate the heat transfer from the flat plate to the fluid. Note that the
heating region begins at the leading edge,
0
0
x
, with reference to Fig.
6.23, and that u is given where
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
2
GG
yy
Uu
(2)
Ans.
The heat transfer rate
w
q from the plate wall to the fluid is given in Eq.
359
6 Newtonian Flow
(6.5.48), and with the given temperature profile in Eq. (1) and the velocity
profile in Eq. (2), we have
f
f
w
w
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
³
f
y
c
TT
wp
w
y
T
k
dy
yyyy
dx
d
TTUcq
22
221
0
GGGG
U
G
G
(3)
Taking into account that for the integration over the thermal boundary
layer thickness
T
G
9GGGGG
|
f
f
T
yy 00
(4)
so that Eq. (3) can be written as
9G
99
GU
f
f
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
TTk
dx
d
TTUc
wc
wp
2
306
32
(5)
where
G
G
9
T
is the boundary thickness ratio. Eq. (5) is further reduced
to the form after differentiation to write
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
p
c
c
k
Udx
d
UG
9
9
G
2
56
1
4
3
(6)
For the velocity profile in Eq. (2), we have (see Problem 6.5.1)
U
x
U
K
G
0
2
30
or
2
1
5.5
x
Re
x
G
(7)
and
Udx
d
U
KG
G
0
15
(8)
Substituting Eq. (8) for Eq. (6), and after rearranging, we have a non-
dimensional equation
1
4
3
80
5
4
5
| Pr
k
.
X
9
9
D
(9)
where
D
k is the thermal diffusivity
pc
ckk
U
D
and P
r
is the Prandtl
number. The solution in Eq. (9) for
9
with P
r
being not too far from
360

Exercise
unity is obtained to be
3
1
| Pr
9
(10)
Thus the local heat transfer
w
q is written with the aid of Eqs. (7) and (10)
as
x
PrRe
TTkq
x
w
cw
5.5
2
3
1
2
1
f
|
(11)
Furthermore, the local Nusselt number can be obtained as
3
1
2
1
3640 PrRe
TTk
xq
Nu
x
w
c
w
x
.
f
(12)
For comparison reasons it is quoted that the analytical solution is available
in Schlichting (1955), for
x
Nu to give
3
1
2
1
3390 PrReNu
xx
.
(13)
The difference is not as large as obtained in Eq. (12) from the guessed pro-
file method.
In two dimensional boundary layer flow, if P
r
is not far from unity,
there exists a relationship between the heat flux
w
q and the wall shear
stress
w
W
as follows
w
c
w
w
c
w
w
du
dTk
y
u
y
T
k
q
0
0
K
K
W
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
(14)
where it is assumed that the behavior of u and
T
in the boundary layer is
similar. The relation (14) is known as the Reynolds’ analogy. Considering
Eq. (11) in Exercise 6.5.1 and Eq. (12) in Exercise 6.5.2 to Eq. (14), we
can relate
x
Nu (representing
w
q ) and
f
c (representing
w
W
) as follows
3
1
2
1
PrRecNu
xfx
(15)
For 1 P
r
, we have the relationship
361

6 Newtonian Flow
xfx
RecNu
2
1
(16)
Equation (16) is the simplest form of the Reynolds’ analogy. It is of inter-
est to consider that the expression Eq. (15) is expanded in more general
form of the Reynolds’ analogy, which is valid for all laminar boundary
layer flow, and is written as
),( Pr
l
x
fRecNu
xfx
2
1
(17)
where
)( Prlxf , is a function determined by experiments or analysis. It is
noted that frequently in practice, the Stanton number Sn (the local Stanton
number
x
Sn ) is used instead of the Nusselt number, which is defined as
PrRe
Nu
Sn
x
x
x
(18)
Using
x
Sn , Eq. (15) it is written as
3
2
2
1
PrcSn
fx
(19)
Problems
6.5-1. The guessed laminar and turbulent velocity profiles in the boundary
layer on a flat plate with a zero attack angle is given by the parabolic
and the 1/7-power law respectively as follows
2
2 )()(
GG
yy
U
u
; laminar
(1)
and
7
1
)(
G
y
U
u
; turbulence
(2)
Show that
(i)
for a laminar flow;
5
105ud
ex
R
362

Problems
2
1
5.5
|
x
xRe
G
(3)
2
1
73.0
|
xf
Rec
(4)
(ii) for a turbulent flow;
75
101105 uddu
x
Re
5
1
38.0
|
x
xRe
G
(5)
5
1
059.0
|
xf
Rec
(6)
6.5-2. Define the boundary layer thickness ,
G
the displacement thickness
G
c
and the momentum thickness
T
, and give the physical interpreta-
tion by discussing the importance of the three thicknesses.
6.5-3. Give the limitation of applying the boundary layer theory to an ac-
tual viscous flow over a bluff body.
6.5-4. For a flat plate with a zero attack angle, calculate the boundary layer
thickness at a point of m5.0 x from the leading edge, if the free
stream velocity of air is
sm05.0 U
, where the density is
3
mkg161.
U
and the kinematic viscosity is
s
25
m10601
u .
X
.
Also, predict the net drag force for one side of the plate if the surface
is 2 m wide and 4 m long. Is the flow laminar or turbulence? If the
free stream velocity of the inviscid core flow is increased to
sm5 U , predict the net drag force, taking into account of the
laminar portion, where
5
105 ud
x
Re . Use relations in Problem 6.5-
1 (to be more precise relations Exercise 6.6.1 may be used and also
see Problem 6.6-4).
Ans.
»
»
»
¼
º
«
«
«
¬
ª
|
N5530m05For
N142
m0701560050For
.,.
.
.,,.
D
D
x
FsU
F
laminarResmU
G
363
