Яковлев В.В. Экологическая безопасность, оценка риска

Подождите немного. Документ загружается.

141

Максимальное значение среди всех значений h

равно 4.5, т.е. реко-

мендуется стратегия А

В общем случае выбор критерия – процесс субъективный. Наилуч-

ший выход из этой ситуации состоит в том, чтобы рассчитать оптималь-

ную стратегию (выбрать наилучшее решение в условиях неопределенно-

сти) по всем трем критериям. Если в своем большинстве, в пределах до-

пустимых отклонений, решения совпадают, можно считать, что выбор оп-

тимальной стратегии

оказался удачным. Даже в том случае, когда решения

по трем критериям существенно расходятся, процесс принятия решения

поможет глубже осознать суть задачи и облегчит ее решение.

В частности, обобщая представленные выше расчеты примера 7.7,

можно сделать вывод о том, что в большинстве случаев в качестве реко-

мендуемой выступает стратегия А

Пример 7.13.

Требуется найти оптимальное решение в условиях неопределенно-

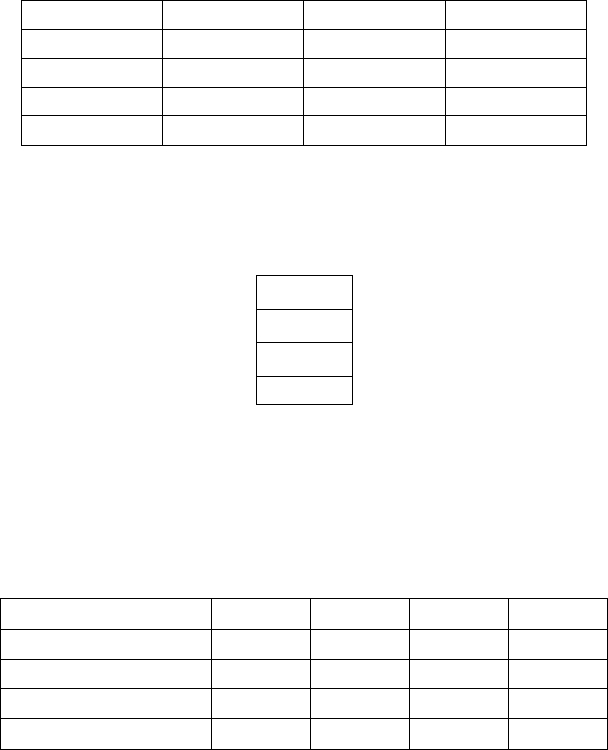
сти. Платежная матрица имеет вид, представленный табл. 7.20.

Таблица 7.20.

А\П

0.20 0.30 0.15

0.75 0.20 0.35

0.25 0.80 0.25

0.85 0.05 0.45

1. Решение на основе критерия Вальда.

В каждой строке находим наименьший выигрыш (табл. 7.21).

Таблица 7.21.

=0.15

=0.20

=0.25

=0.05

Среди этих значений находим максимальное: V=0.25, что соответст-

вует рекомендации выбирать в качестве оптимальной стратегию А

2. Решение на основе критерия Сэвиджа.

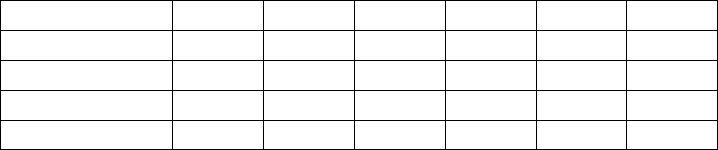
Построим матрицу рисков и добавим справа столбец, в котором за-

пишем максимальное значение риска для каждой стратегии (табл. 7.22).

Таблица 7.22.

А\П

0.65 0.50 0.30 0.65

0.10 0.60 0.10 0.60

0.60 0 0.20 0.60

0 0.75 0 0.75

142

Минимальное значение риска по всем стратегиям равно R

= 0.6, что

соответствует рекомендации о выборе в качестве оптимальной стратегии

или А

3. Решение на основе критерия Гурвица.

Принимаем значение коэффициента k = 0.6.

Построим новую матрицу, добавив к исходной три столбца справа, в

которых соответственно запишем:

– - пессимистическую оценку a

каждой i-й стратегии

aa min

– оптимистическую оценку w

каждой i-й стратегии

aw max

– их среднее взвешенное h

iii

wkakh

⋅

−

⋅

= )1(

(7.52)

Максимальное число среди значений h

(табл. 7.23) будет соответст-

вовать оптимальной стратегии.

Таблица 7.23.

А\П

0.20 0.30 0.15 0.15 0.30 0.21

0.75 0.20 0.35 0.20 0.75 0.42

0.25 0.80 0.25 0.25 0.80 0.47

0.85 0.05 0.45 0.05 0.85 0.37

Среди всех h

максимальное значение имеет h

= 0.47. Следователь-

но, согласно критерию Гурвица в качестве оптимальной следует выбирать

стратегию А

Таким образом, в рассмотренном примере все три критерия сходятся

в решении и рекомендуют выбор стратегии А

Изложенные выше методы рассматривали выбор решения в чистых

стратегиях стороны А.

Аналогичные подходы могут быть рекомендованы для определения

оптимальных вариантов поведения стороны А в смешанных стратегиях.

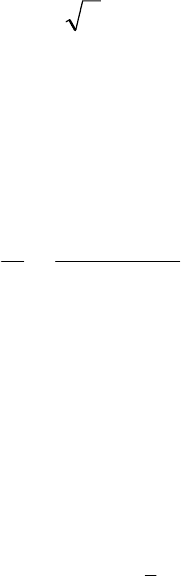
143

8. Интервальное оценивание числовых характеристик

и параметров распределения

генеральной совокупности [49, 50, 51].

8.1. Законы распределения случайных величин и их параметры

Группированный статистический ряд.

Пусть имеется выборка (х

min

, х

,…, х

max

) из генеральной сово-

купности Х.

Промежуток [х

min

, x

max

] делится на некоторое число k равных по дли-

не промежутков. Обозначим эти промежутки слева направо через:

∆∆∆ ,...,,

[

]

(

]

(

]

max12121min1

,...,,,,, xaaaax

kk −

∆

=∆=∆

Здесь принято: а

= х

min

, a

= x

max

Пусть n

– число элементов выборки, попавших в промежуток ∆

Числа n

, n

… n

называют частотами попадания элементов выборки в рас-

сматриваемые промежутки.

Определение 1. Совокупность промежутков

∆∆

∆

,...,,

и соот-

ветствующих им частот называется группированным статистическим

рядом.

Для определения числа k промежутков рекомендуется следующая

полуэмпирическая формула:

72.1 nk ⋅≈

где n – объем выборки, как правило n ∈ [30, 100].

Применяется также формула Старджесса:

(

)

nk lg3.31 ⋅+≈

Длина h промежутков

∆

,...,,

определится через размах R вы-

борки соотношением:

minmax

−

Вместо группы элементов, попавших в конкретный интервал ∆

, мо-

жет рассматриваться один их представитель. В качестве такого представи-

теля выбирается средняя точка

∗

x промежутка ∆

Группированный статистический ряд обычно представляют в виде

таблицы, что удобно выполнять в Excel.

Определение 2. Выборочной оценкой генеральной числовой характе-

ристики называется ее приближенное значение, найденное по выборке.

Основными оценками являются:

Выборочное среднее

, которое является оценкой генерального математи-

ческого ожидания m = M[X]:

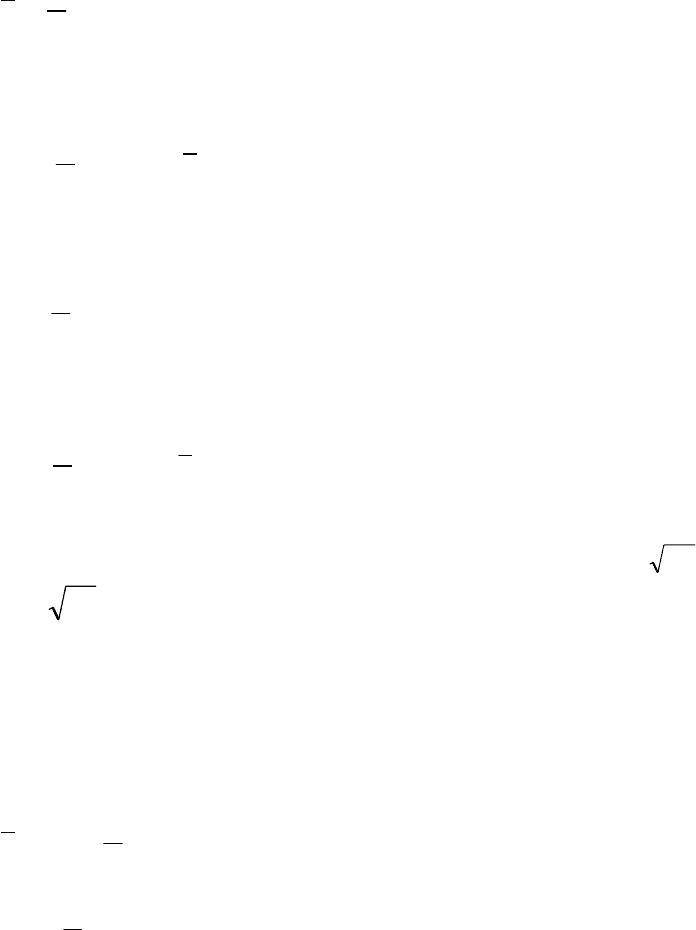
144

∑

⋅=

(8.1.1)

Выборочный центральный момент s

порядка d, который является оценкой

генерального центрального момента порядка d (µ

= M[(X-m)

] ):

()

∑

−⋅=

(8.1.2)

Выборочный начальный момент a

порядка t, который является оценкой

генерального начального момента порядка t α

= M(X

∑

⋅=

(8.1.3)

Выборочная дисперсия s

, которая является оценкой генеральной диспер-

сии σ

= µ

()

∑

−⋅=

(8.1.3)

Выборочное среднее квадратическое отклонение s, которое является оцен-

кой генерального среднего квадратического отклонения

σσ

= :

ss =

(8.1.4)

С помощью группированного статистического ряда можно при-

ближенно вычислить выборочные моменты. Так как группа элементов

выборки, входящих в промежуток

∆

, заменяется средней точкой

∗

x про-

межутка, то следует полагать, что элемент

∗

как бы встречается в

выборке n

раз, т.е. имеет частоту n

. Получаем следующие формулы:

∑

∗

⋅⋅≈=

()

iif

∑

∗

⋅⋅≈

где n

– число элементов выборки, попавших в промежуток ∆

n – объем выборки

Применение этих формул целесообразно при ручных расчетах.

8.2. Метод максимального правдоподобия оценок параметров гене-

рального распределения

Пусть известен вид закона генерального распределения, а параметры

,..,,

в него входящие, неизвестны. Возникает задача их статистиче-

ской оценки.

Метод максимального правдоподобия, созданный английским мате-

матиком Р. Фишером (1890-1962), является достаточно универсальным.

145

Пусть имеется выборка (х

, х

,…, х

) из генеральной совокупности с

плотностью вероятности f(x,θ), содержащей один неизвестный параметр θ.

Выборка является n-мерной случайной величиной, компоненты x

которой взаимно независимы, одинаково распределены с плотностью

f(x,θ), следовательно, на основе теоремы умножения плотностей распреде-

ления случайных величин, плотность распределения n-мерной случайной

величины (х

, х

,…, х

) будет равна:

),(),(),();,...,,(

2121

xfxfxfxxxL "

⋅

(8.2.1)

Эта функция называется функцией правдоподобия для рассматри-

ваемой выборки.

Будем считать θ неслучайной переменной величиной, а элементы

, х

,…, х

выборки – фиксированными, т.к. выборка фактически осущест-

влена. Если придать θ различные значения, то естественно ожидать, что

плотность L(x

, x

,…, x

; θ) примет максимальное значение в случае, когда

значение θ окажется равным истинному

значению, т.к. при других значе-

ниях θ менее вероятно за один раз получить именно данную выборку.

Эти интуитивные соображения приводят к тому, что за оценку θ при-

нимают такое его значение, при котором функция правдоподобия L(•) дос-

тигает максимума

Поскольку L(•) состоит из произведений, то технически удобнее ис-

кать максимум логарифма:

(

)

);,...(lnmax

xxL

, учитывая, что точка

доставляющая максимум ln(L(•)), доставляет максимум и функции L(•).

Тогда, для определения

составляем уравнение:

()

[]

;,...ln

∂

xxL

которое называется уравнением правдоподобия, а его решение

()

xxx ,...,,

θθ

зависящее от элементов выборки, называют оценкой максимального прав-

доподобия.

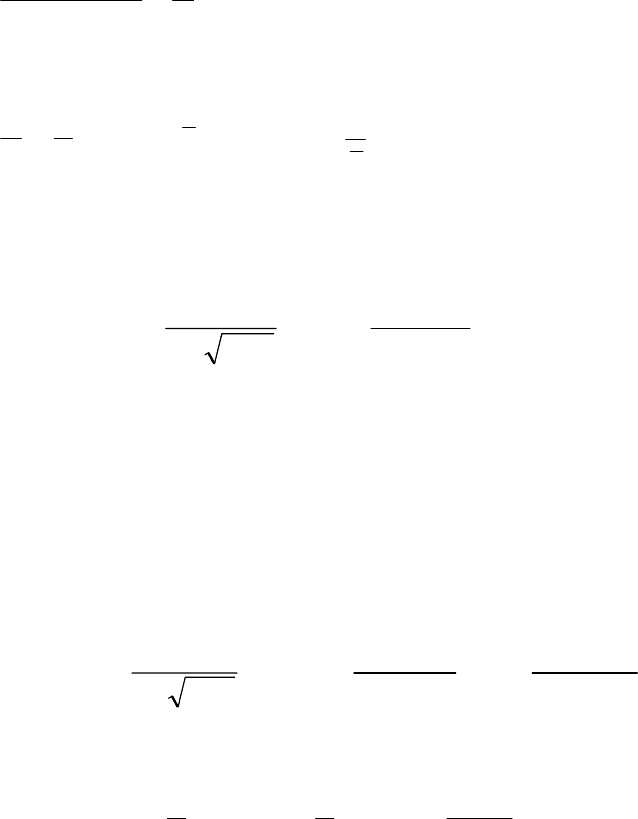
В случае, когда генеральная плотность вероятности содержит k па-

раметров,

то вместо одного уравнения правдоподобия решается система

уравнений:

)ln(

,....,0

)ln(

∂

θθ

(8.2.2)

Рассмотрим несколько типовых примеров.

146

Пример 8.2.1.

Показательный закон с плотностью:

()

0,exp),( ≥⋅−

⋅

= xдляxxf

Функция правдоподобия при х > 0 имеет вид:

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅=⋅⋅=

∑

⋅−

xeexxxL

exp),,...,,(

λλλλ

После логарифмирования:

∑

⋅−⋅=

xnxL

)ln(),(ln

λλλ

Находится частная производная функции L(λ, x) по переменной λ:

()

[]

,ln

=−=

∂

∑

nxL

λλ

отсюда:

=⋅=

∑

, или

Пример 8.2.2.

Нормальный закон распределения с плотностью:

(

)

⎥

⎦

⎤

⎢

⎣

⎡

⋅

−

−⋅

⋅⋅

exp

),,(

πσ

mxf

где m – математическое ожидание случайной величины Х генераль-

ной совокупности;

σ - среднее квадратическое отклонение случайной величины Х

генеральной совокупности.

В данном случае имеется два параметра m и σ

. Следовательно,

функция правдоподобия L(m, σ) имеет вид:

(

)

(

)

⎥

⎦

⎤

⎢

⎣

⎡

⋅

−

−−

⋅

−

−⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

exp

),(

σσ

πσ

После логарифмирования:

()

∑

−⋅

⋅

−⋅−⋅⋅−=

2ln

),(ln

σπσ

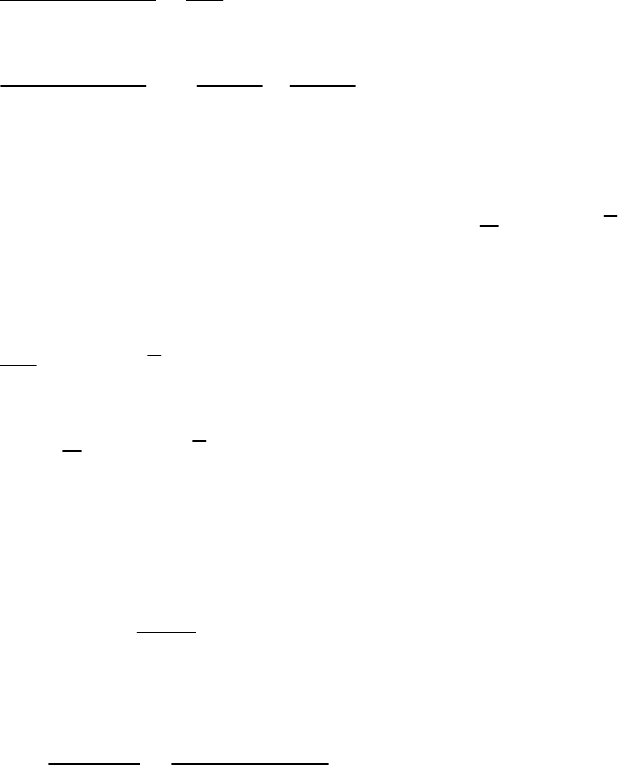
147

Далее, дифференцируя [ln(L(m, σ)] по m и σ

, получаем систему

уравнений правдоподобия:

()

∑

=−

⋅

−=

∂

=−⋅=

∂

nmL

422

),(ln(

1)),(ln(

σσσ

Из первого уравнения находим:

=⋅−

∑

mnx

, откуда получаем

=⋅=

∑

Из второго уравнения:

()

sxx

nxx

=−⋅=

=−⋅

∑

Пример 8.2.3.

Равномерное распределение с плотностью:

[]

baxпри

baxf ,,

),,( ∈

−

Функция правдоподобия в этом случае имеет вид:

()()

xxab

minmax

−

≤

−

Необходимо найти такие значения (a, b), которые доставляют функ-

ции правдоподобия максимум.

Из последнего неравенства следует, что функция L(a,b) принимает

максимальное значение при b = x

max

и a = x

min

. Таким образом, оценками

максимального правдоподобия в случае равномерного закона распределе-

ния являются:

maxmin

, xbxa ==

Пример 8.2.4.

Распределение Пуассона.

В случае дискретного закона распределения ),()(

xpxXP =

функ-

ция правдоподобия определяется зависимостью:

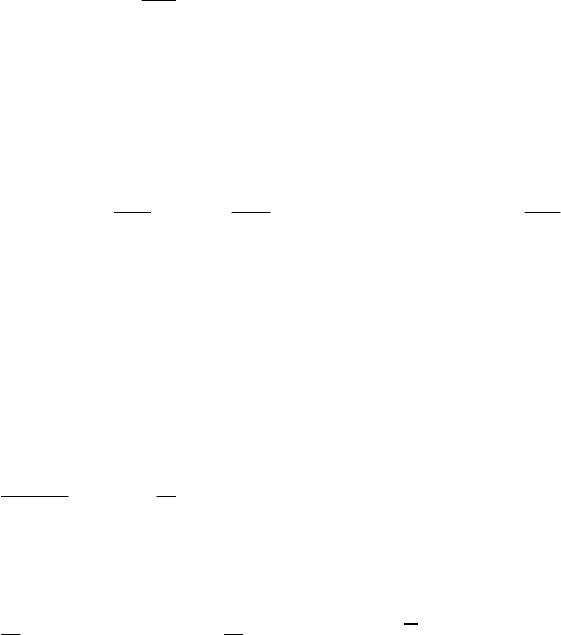
148

()

∏

xpхL

),(,

θθ

Вероятность того, что случайная величина Х, распределенная по за-

кону Пуассона, реализуется ровно k раз:

)exp(

)( a

kXP

−⋅==

В этом случае необходимо найти такое значение параметра а, для ко-

торого функция правдоподобия L(a) достигнет своего максимума.

Тогда функцию правдоподобия можно представить в виде:

∏

−−

⋅⋅−=⋅⋅=

ane

aхL

)exp(

),(

После логарифмирования:

()

∑∑

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅+⋅−=

xxаanaL

!ln)ln()(ln

Находим частную производную функции ln(L(a)) по аргументу а:

1ln

=⋅+−=

∂

∑

Откуда:

хax

anx

=⋅==⋅

∑∑

8.3. Проверка гипотезы о законе распределения

генеральной совокупности.

Вначале выдвигается гипотеза о виде закона распределения, который

может быть нормальным, Пуассона и т.д.

После того, как выбран вид закона распределения, возникает задача

оценки его параметров и проверки закона в целом.

Наиболее обоснованным и часто используемым является метод с ис-

пользованием критерия

(хи-квадрат), введенный английским статисти-

ком К. Пирсоном (1900 г.) и существенно уточненным английским матема-

тиком Р. Фишером (1924 г.).

Ограничимся случаем одномерного распределения.

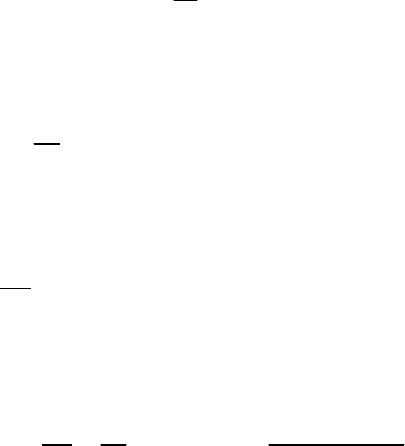
149

Пусть выдвинута гипотеза Н

о генеральном законе распределения с

функцией F(x). Конкурирующей гипотезой является гипотеза о справедли-

вости одного из конкурирующих распределений.

Случай первый.

Параметры проверяемого закона полностью известны.

Разобьем генеральную совокупность, т.е. множество значений изу-

чаемой случайной величины Х, на k непересекающихся промежутков

∆∆∆ ,...,,

. Обозначим через p

вероятность того, что Х∈∆, )(

XPp

∆

∈

= ,

i = 1, 2,…, k. Если генеральная совокупность – вся вещественная ось, то

подмножества

[

)

iii

aa ,

1−

∆ - полуоткрытые промежутки, i= 2, 3, …, k-1.

Крайние промежутки будут полубесконечными:

()

[

)

∞

=∞−= ,,,

kk10

aa ∆∆

Отметим, что

∑

p . Будем полагать, что все р

> 0.

Пусть далее n

, n

, … , n

– частоты попадания выборочных элемен-

тов в соответствующие промежутки. В случае справедливости гипотезы Н

относительные частоты

при большом n должны быть близки к вероят-

ностям р

(i = 1, 2, …, k), поэтому за меру отклонения выборочного рас-

пределения от гипотетического с функцией F(x) выбирают величину:

∑

⎟

⎠

⎞

⎜

⎝

⎛

−⋅

, (8.3.1)

где с

– некие положительные числа (веса).

К. Пирсоном в качестве весов выбраны числа:

),...,,( ki

21==

Тогда получается следующее выражение статистики критерия хи-

квадрат К. Пирсона:

(

)

∑∑

⋅

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

−⋅=χ

pnn

(8.3.2)

(статистика обозначена тем же символом, что и закон распределения

хи-квадрат)

Закон распределения хи-квадрат появляется в теории вероятностей

при изучении суммы квадратов нескольких (k) взаимно независимых нор-

мально распределенных случайных величин Х

, Х

, …, Х

с одинаковыми

параметрами распределения: m = 0, σ = 1.

1 k

XXXZ +++= ...

150

Доказано, что случайная величина Z распределена по закону хи-

квадрат с k степенями свободы. Числом степеней свободы функции назы-

вается число ее независимых аргументов.

Закон распределения хи-квадрат обозначается

)(k

χ . Плотность ве-

роятности этого закона определяется формулой для х ≥ 0:

≥≥

⎟

⎠

⎞

⎜

⎝

⎛

−⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

Γ⋅=

−

kxдля

,exp)(

(8.3.3)

Теорема К. Пирсона.

Статистика (8.3.2) критерия χ

асимптотически при n → ∞ распреде-

лена по закону χ

с (k-1) степенями свободы.

Аргументами статистики χ

являются частоты n

, n

,…, n

. Эти час-

тоты связаны равенством:

nnnn

++ "

следовательно, функция χ

имеет (k-1) независимых аргументов.

Случай второй.

Параметры проверяемого закона распределения неизвестны.

Параметры закона распределения могут быть оценены по методу

максимума правдоподобия. Справедлива теорема Р. Фишера.

Теорема Р. Фишера. Статистика (8.3.2) при n → ∞ асимптотиче-

ски распределена по закону

с числом степеней свободы r:

,1−−= lkr

где l – число параметров, оцененных по выборке.

Замечание.

Суждение о принятии или отвержении выдвинутой статистиче-

ской гипотезы не являются абсолютными, а носят вероятностный ха-

рактер. Принимая или отвергая гипотезу, могут быть совершены ошиб-

ки.

Ошибкой первого рода называется ошибка отвержения правильной

гипотезы.

Ошибкой второго рода называется ошибка принятия неверной ги-

потезы.

Уровнем значимости называется такое значение вероятности, что

событие с такой вероятностью практически не реализуется.

Вероятность ошибки первого рода равна уровню значимости

вероятность ошибки второго рода обозначается

По виду статистики

можно заключить, что большие значения

неприемлемы для справедливости гипотезы Н

. Отсюда следует, что

критерий

является правосторонним, а критической областью будет

промежуток вида

(

)

∞+χ

α−

),(r

, где

(

)

)(r

α−

χ - квантиль порядка (1-

) рас-

пределения хи-квадрат с r степенями свободы (рис. 8.3.1).