Яковлев В.В. Экологическая безопасность, оценка риска

Подождите немного. Документ загружается.

131

2211

2222112

1221111

≥⋅++⋅+⋅

≥

⋅

+⋅

mmnnn

xaxaxa

""""""""""""""

(7.25)

где х

– неотрицательные переменные.

С учетом (7.24), (7.21) имеет место следующее условие:

...

=+++

xxx

(7.26)

Поскольку сторона А заинтересована в максимальном выигрыше, то

правая часть уравнения (7.26) должна иметь минимальное значение, или

цена игры

должна быть максимальной.

Таким образом, задача решения игры m×n свелась к следующей ма-

тематической задаче.

Определить неотрицательные значения переменных х

, х

, … , х

удовлетворяющих линейным ограничениям (7.25) и доставляющих мини-

мум линейной функции:

xxxxL +++= "

)(

(7.27)

Это типичная задача линейного программирования. Для данной по-

становки она адекватна выбору таких решений, при которых цена игры бу-

дет максимальна.

Для поиска решения в интересах игрока В рассуждения будут иден-

тичными с той лишь разницей, что игрок В стремится минимизировать

выигрыш игрока А, т.е. не минимизировать, а максимизировать величину

.....................................................

2211

2222121

1212111

≤⋅++⋅+⋅

≤

⋅

+⋅

nmnmm

yayaya

(7.28)

где неотрицательные переменные y

имеют вид:

ννν

y === ...,,,

(7.29)

Требуется найти такие значения переменных y

, при которых в усло-

виях ограничений (7.28) обращается в максимум линейная функция:

)(

=+++=

yyyyL "

(7.30)

Вместо максимума функции L(y) можно искать минимум

функции

yyyyLyL −−−−=−=−= "

)()(

(7.31)

132

Таким образом, решение игры m×n удалось свести к двум задачам

линейного программирования.

Нетрудно заметить, что решение задачи линейного программирова-

ния всегда (в данных условиях игры) существует.

Применяя изложенный подход к задаче «три пальца» получим сле-

дующее решение:

321

=ν

∗

);,,(),,(

qqqS

pppS

(7.32)

Игры с природой.

При исследовании операций в процессе принятия решений в услови-

ях неопределенности приходится сталкиваться с ситуациями, в которых

противник не руководствуется разумом, т.е. противодействие перестает

быть осознанным.

Во всех случаях, когда принятие решения зависит не от сознательно

противодействующего противника, а от случайной объективной действи-

тельности, модели

операций принятия решений носят общее название «иг-

ры с природой».

Рассмотрим такого рода ситуацию.

Пусть сторона А имеет m возможных стратегий А

, А

, … , А

В качестве стратегий «природы» можно сделать n предположений:

, П

,…,П

(7.33)

Выигрыш стороны А в каждой паре выбранных стратегий задается

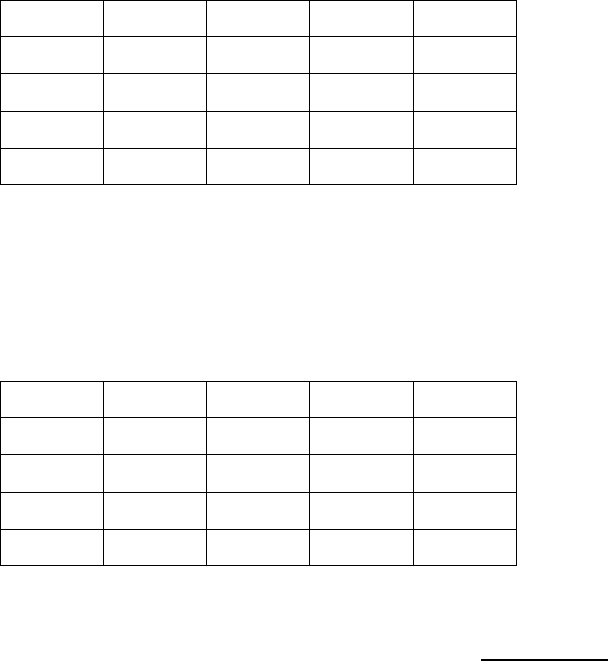
платежной матрицей (табл. 7.8).

Таблица 7.8.

Платежная матрица игры с природой.

Требуется выбрать такую стратегию стороны А (чистую или сме-

шанную), которая является предпочтительной.

Отсутствие разумного противодействия не облегчает решение по-

ставленной задачи. В конфликтной ситуации предположение о диамет-

ральной противоположности

интересов в какой-то степени снижало зна-

чимость неопределенности.

A\П

… П

… a

…

… … … …

… a

133

Рассмотрим типичные ситуации игр с природой.

Ситуация 1. Наиболее простым случаем принятия решения в услови-

ях неопределенности является случай, когда одна из стратегий стороны А

доминирует перед остальными.

Пример 7.5.

Рассмотрим игру 4×4, заданную платежной матрицей (табл. 7.9).

Таблица 7.9.

Вид заданной платежной матрицы.

А\П

-2 -1 0 +2

+4 +1 +1 +2

0 +1 +1 -2

+4 +1 -1 -1

Преобразуем заданную платежную матрицу, прибавив к каждому ее

элементу +3. Получим матрицу (табл. 7.10) с положительными значениями

выигрышей.

Таблица 7.10.

Выбор доминирующей стратегии стороны А в игре 4×4.

А\П

1 2 3 5

7 4 4 5

3 4 4 1

7 4 2 2

Анализ стратегий стороны А показывает, что при выборе стратегии

при любом состоянии «природы» П

выигрыш будет не меньше чем при

любой другой стратегии А

. Стратегия А

является предпочтительной (до-

минирующей) в сравнении с остальными стратегиями стороны А.

Если в матрице нет доминирующих стратегий, то игру следует про-

анализировать для определения стратегий, заведомо невыгодных или дуб-

лирующих друг друга. Такие стратегии можно исключить из дальнейшего

рассмотрения.

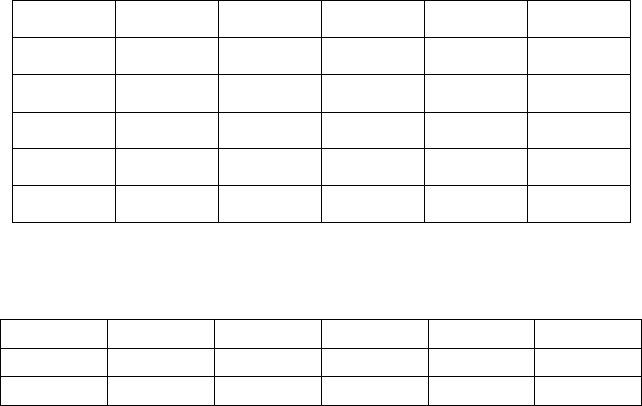
Пример 7.6.

Рассмотрим игру 5×5, заданную платежной матрицей (табл. 7.11).

Анализ игры показывает,

что можно отбросить стратегии А

и А

как заведомо невыгодные в сравнении со стратегией А

. Стратегия А

не

выгодна в сравнении со стратегией А

, т.е. стратегия А

тоже может быть

исключена из дальнейшего участия в решении задачи. В результате полу-

чаем платежную матрицу в следующем виде (табл. 7.12).

134

Таблица 7.11.

Исходная платежная матрица игры 5×5.

А\П

5 3 4 2 1

5 3 2 1 1

1 2 5 4 3

7 6 7 3 1

1 2 3 4 3

Таблица 7.12.

Окончательный вид приведенной платежной матрицы.

А\П

1 2 5 4 3

7 6 7 3 1

Таким образом, игру 5×5 удалось свести к более простой игре 2×5.

Следует заметить, что при рассмотрении игры с разумным против-

ником за него можно было бы отбросить стратегию П

как невыгодную в

сравнении со стратегией П

. Но в рассматриваемой задаче «природа» не

выбирает свою стратегию таким образом, чтобы как можно больше «на-

вредить» стороне А, следовательно, упрощение игры за счет исключения

«невыгодных для природы» стратегий недопустимо.

Далее будем полагать, что априорное упрощение игры и преобразо-

вание платежной матрицы выполнено.

Заметим, что картина игры с природой, которую

представляет пла-

тежная матрица, содержит некоторые искажения. Предположим, что выиг-

рыш при выборе стратегии A

для состояния природы П

больше, чем для

пары A

, П

kgij

aa >

(7.34)

Однако первый выигрыш может быть больше второго не за счет то-

го, что стороной А выбрана более удачная стратегия, а за счет того, что со-

стояние природы П

«выгоднее» для стороны А. Например, отсутствие сти-

хийных бедствий выгоднее при проектировании объекта, чем наводнение

или землетрясение.

Представляется целесообразным ввести такие показатели, которые

отображали бы степень «удачливости» выбора стратегии с учетом того,

насколько она благоприятна для нас.

С этой целью в теории принятия решений вводится понятие риска.

Риском игрока А

при использовании стратегии А

в условиях П

назы-

вается разность между выигрышем, который он получил бы, если бы дос-

товерно знал состояние П

, и выигрышем, который игрок А получит в

сложившихся условиях, применяя стратегию А

135

Т.е. если сторона А знает достоверно, что произойдет именно ситуа-

ция П

, то она может применить стратегию, отличную от А

Обозначим через r

риск игрока А при выборе стратегии А

в услови-

ях П

. Выразим значение риска через элементы платежной матрицы. Оче-

видно, если бы игрок А знал заранее состояние «природы» П

, он выбрал

бы такую стратегию, которой соответствует максимальный выигрыш α

данном j-м столбце:

aa max

(7.35)

Тогда значение риска можно определить с помощью соотношения:

ijij

ijjij

aaaar

−

max

(7.36)

Из этого соотношения следует, что

0≥

(7.37)

Матрица рисков зачастую дает более благоприятное представление о

неопределенной ситуации, чем исходная платежная матрица.

Пример 7.7.

Планируется операция по реабилитации удаленного земельного уча-

стка, загрязненного неизвестными веществами. Предполагается, что это

могла быть нефть, бензин, керосин, бензол. Средства, необходимые для

приведения земли в состояние, пригодное для пользования (например, сор-

бенты), могут состоять

из трех комплектов. Платежная матрица (табл.7.11)

содержит «выигрыши» в виде, например, очищенной площади (га) в еди-

ницу времени (месяц).

Требуется построить матрицу рисков.

Таблица 7.11.

Вид платежной матрицы в задаче 3×4.

А\П

1 4 5 9

3 8 4 3

4 6 6 2

Таблица 7.12.

Вид матрицы рисков в той же задаче.

А\П

3 4 1 0

1 0 2 6

0 2 0 7

При анализе матрицы рисков и ее сравнении с платежной матрицей

можно сделать следующие выводы.

В платежной матрице элементы а

и а

равны:

2421

аа

га

Однако, они неравноценны по степени «удачливости» выбора стра-

тегии А

: при состоянии участка П

можно было реанимировать 4 га, вы-

136

брав стратегию А

и с выбором стратегии А

можно было бы согласиться,

но при состоянии участка П

можно было обработать 9 га, выбрав ком-

плект А

, т.е. выбор стратегии А

нельзя признать удачным.

До сих пор все действия были связаны, в основном, с группировкой

исходных данных. Вместе с тем принятие решений в играх с природой ба-

зируется на определенных критериях.

Критерии, основанные на известных вероятностях состояний.

Если известны вероятности Р состояний природы Q

∑

jjj

QПPQ

1);(

, (7.38)

то за показатель эффективности, который сторона А стремится обратить в

максимум, следует выбрать математическое ожидание выигрыша. Обозна-

чим это среднее значение для i-й стратегии через

∑

⋅=

ijji

aQa

(7.39)

В качестве оптимальной стратегии выбирают такую стратегию i

∗

, для

которой значение

будет максимально:

∗∗

⇒= iaa

max

(7.40)

Пример 7.8.

Обратимся к исходным данным примера 7.7. Его платежная матрица имеет вид

(табл. 7.13):

Таблица 7.13.

А\П

1 4 5 9

3 8 4 3

4 6 6 2

Добавим данные по вероятностям Q

в дополнительной строке и по

значениям математических ожиданий выигрышей для каждой стратегии в

дополнительном столбце. Получим новую матрицу (табл. 7.14):

Таблица 7.14.

А\П

1 4 5 9

5.2

3 8 4 3 4.5

4 6 6 2 5.0

0.1 0.2 0.5 0.2

137

Очевидно, решением игры является стратегия А

1,2.5 ==

∗∗

(7.41)

В тех же условиях можно пользоваться средним риском, который на-

до минимизировать:

∑

⇒⋅=

ijji

rQr

min

(7.42)

Докажем, что оптимальные стратегии, выбранные по значению сред-

него риска и по математическому ожиданию выигрыша, совпадают.

∑∑∑∑∑

=====

⋅+⋅−⋅=−⋅+⋅=+

jjijj

ijj

ijjjijjii

QaQaQaQaQra

11111

)(

ββ

∑

⋅=+

jjii

Qra

(7.43)

Заметим, что среднее взвешенное столбцов, т.е. сумма

∑

⋅

представляет собой константу:

CconstQ

==⋅

∑

(7.44)

Становится ясным, что среднее взвешенное значение риска обраща-

ется в минимум тогда, когда среднее взвешенное значение выигрыша об-

ращается в максимум. Следовательно, утверждение о совпадении опти-

мальных стратегий, выбранных по этим двум показателям, справедливо.

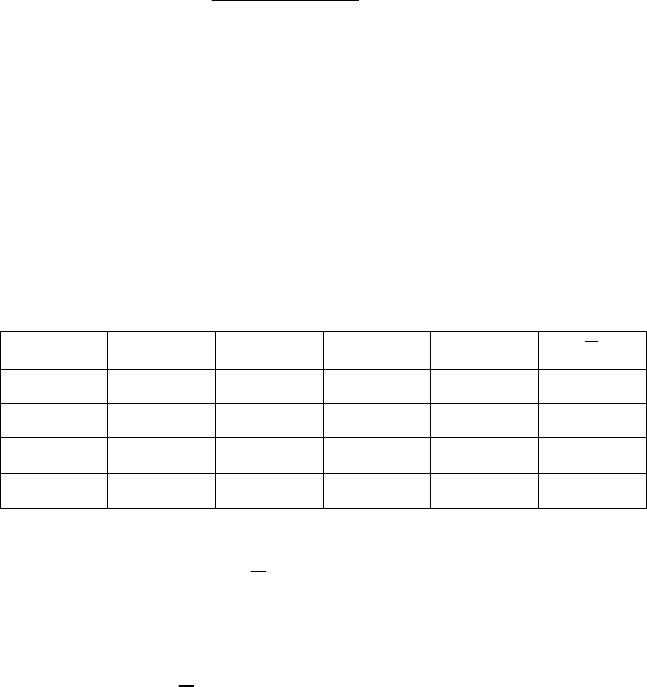
Убедимся в справедливости доказанного на числовом примере. Вер-

немся к исходным данным примера 7.7.

Матрица рисков с

дополнительной строкой вероятностей реализации

различных состояний природы и дополнительным столбцом значений

среднего риска имеет вид (табл. 7.15):

Таблица 7.15.

Расширенная матрица примера 7.7.

А\П

3 4 1 0 1.6

1 0 2 6 2.3

0 2 0 7 1.8

0.1 0.2 0.5 0.2

Минимальное значение среднего риска, равное 1.6 соответствует

первой стратегии, что подтверждает справедливость ее выбора в качестве

оптимальной по критерию среднего риска.

Однако, вероятности Q

состояний природы практически редко бы-

вают известными.

138

Чтобы субъективные представления о вероятностях состояний при-

роды были более-менее правдоподобными, можно найти их численные

значения, используя знание существа явлений и простые математические

приемы, что особенно эффективно в случае оценки состояний природы по

многократным наблюдениям или измерениям.

Если нельзя отдать предпочтения ни одному предположению о со-

стоянии природы, то следует

использовать «Принцип недостаточного ос-

нования Лапласа», т.е. назначить равные вероятности для каждого предпо-

ложения:

∑

====

QQQQ

1,"

(7.45)

Часто встречаются ситуации, когда можно расставить предпочтения

в предположениях о состоянии природы, например, расположив их в по-

рядке убывания пропорционально членам арифметической прогрессии:

1::)2(:)1(:::::

321

−

nnnQQQQ

(7.46)

Откуда, учитывая, что вероятности состояний природы составляют

полную группу событий и их сумма равна единице, получим:

)1(

)1(2

+⋅

−

⋅

, j=1, 2,…, n. (7.47)

Пример 7. 9.

Вернемся к исходным данным примера 7.7.

Для n=4 рассчитаем по формуле (7.47) значения соответствующих вероят-

ностей:

= 0.4; Q

= 0.3; Q

= 0.2; Q

= 0.1

Платежная матрица будет иметь следующий вид (табл. 7.16):

Таблица 7.16.

Платежная матрица примера 7.7 с расставленными в порядке убыва-

ния вероятностями состояний.

А\П

1 4 5 9 3.5

3 8 4 3 4.7

4 6 6 2

4.8

0.4 0.3 0.2 0.1

Максимальное значение

∑

⋅=

jiji

paa

среди всех стратегий сторо-

ны А равно:

8.4maxmax

=⋅=

∑

jij

paa

, (7.48)

что соответствует выбору стратегии А

в качестве рекомендуемой.

139

При использовании подобных приемов нельзя забывать о том, что

выбор оптимальных стратегий на основе субъективных вероятностей так-

же будет субъективным.

Часто для оценок вероятностей состояния природы прибегают к оп-

росу экспертов, мнения которых не всегда расходятся столь существенно,

как это зачастую представляется.

Кроме рассмотренного метода принятия решений в условиях неоп-

ределенности

существует еще несколько методов, использующих уникаль-

ные критерии для поиска оптимальной стратегии (оптимального решения).

Максиминный критерий Вальда.

Согласно этому критерию в качестве оптимальной выбирается стра-

тегия, при которой минимальный выигрыш максимален. Т.е. стратегия,

выбранная по этому критерию, гарантирует максимум выигрыша V в наи-

более неблагоприятных (наихудших) ситуациях:

aV minmax

(7.49)

Пример 7.10.

Вновь вернемся к данным примера 7.7.

Платежная матрица с добавленным столбцом минимальных значений

выигрышей каждой стратегии

имеет вид (табл. 7.17).

Таблица 7.17.

А\П

aa min

1 4 5 9 1

3 8 4 3 3

4 6 6 2 2

Максимальное значение среди всех значений

равно 3, что соот-

ветствует выбору в качестве рекомендуемой стратегии А

Изложенный подход продиктован крайним пессимизмом. Согласно

критерию Вальда надо рассчитывать на самое худшее и из худшего выби-

рать лучшее.

Минимаксный критерий Сэвиджа.

Подход Сэвиджа рекомендует в условиях неопределенности выби-

рать стратегию, при которой величина риска R

принимает наименьшее

значение в неблагоприятной ситуации (среди максимальных рисков).

rR maxmin

(7.50)

Пример 7.11.

Еще раз вернемся к данным примера 7.7.

140

Матрица рисков с дополнительным столбцом максимальных значе-

ний приобретает вид (табл. 7.18):

Таблица 7.18.

А\П

rr max

3 4 1 0 4

1 0 2 6 6

0 2 0 7

Минимальное значение риска среди максимальных равно 4, что со-

ответствует выбору стратегии А

Сущность подхода Сэвиджа состоит в том, чтобы любыми путями

избежать большого риска в процессе принятия решений. Критерий Сэвид-

жа, как и критерий Вальда - критерий крайнего пессимизма с той разни-

цей, что Сэвидж худшим объявляет не минимальный выигрыш, а макси-

мальную потерю выигрыша в сравнении с тем, чего можно было бы

дос-

тичь в данных условиях при полной информации.

Критерий пессимизма-оптимизма Гурвица.

Гурвиц рекомендует в условиях неопределенности не руководство-

ваться ни крайним пессимизмом, ни крайним оптимизмом. Критерий Гур-

вица имеет вид:

⎥

⎦

⎤

⎢

⎣

⎡

⋅−+⋅=

akakK max)1(minmax

, (7.51)

где коэффициент k меняется от 0 до 1,

[

]

1,0

∈

При значении k=1 критерий Гурвица обращается в критерий Вальда,

при значении k=0 этот критерий обращается в критерий крайнего опти-

мизма.

Значение коэффициента k выбирается из субъективных соображе-

ний: чем опаснее ситуация, тем больше желание «подстраховаться», тем

ближе к единице выбирается значение коэффициента k.

Пример 7.12.

Обратимся еще раз к данным примера 7.7.

Вид платежной матрицы с

дополнительными столбцами, содержа-

щими необходимые данные для k=0.7, имеет следующий вид (табл. 7.19):

Таблица 7.19

А\П

aa min

aa max

[]

iii

akakh

)1(

⋅

−+⋅

1 4 5 9 1 9 3.4

3 8 4 3 3 8

4.5

4 6 6 2 2 6 3.2