Яковлев В.В. Экологическая безопасность, оценка риска

Подождите немного. Документ загружается.

151

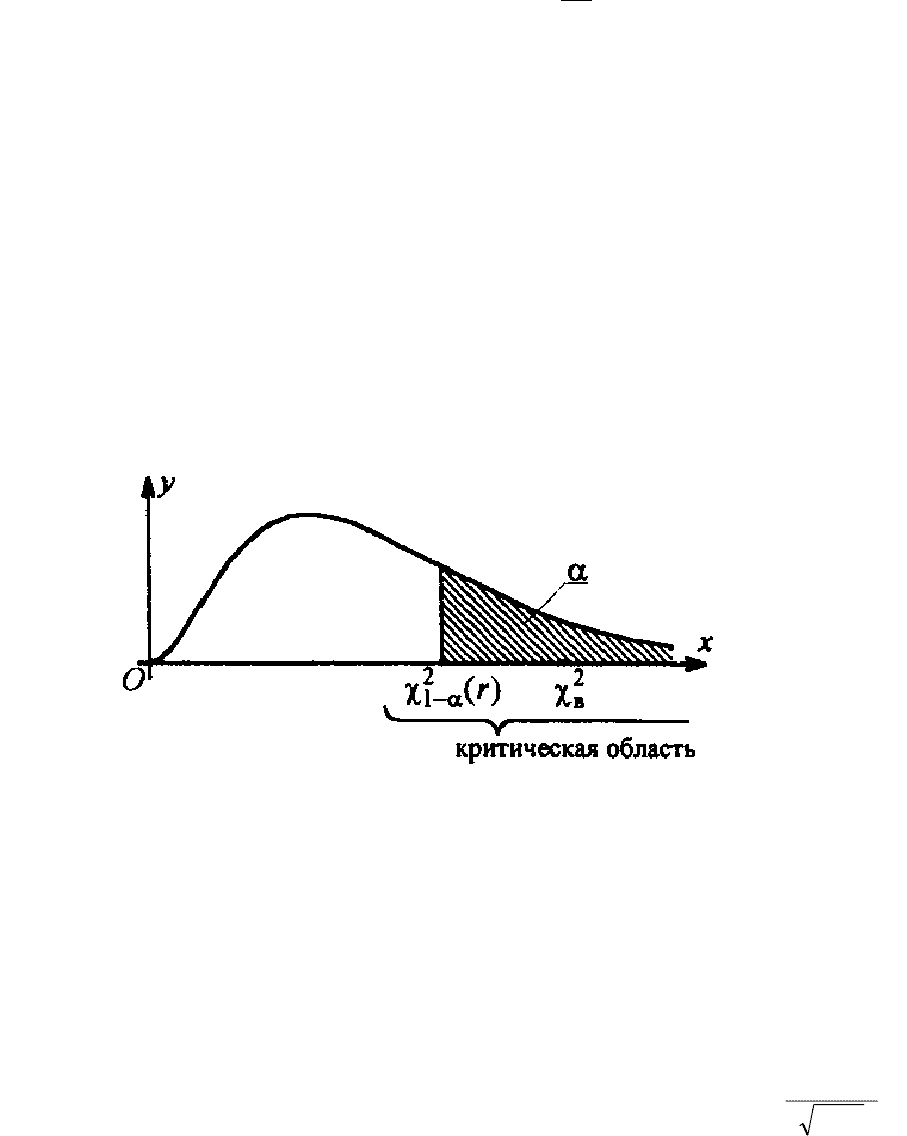
Из формулы (8.3.2) видно, что веса

),...,,( ki

21==

пропор-

циональны n , т.е. с ростом n их значение увеличивается. Таким образом,

если выдвинутая гипотеза Н

неверна, то относительные частоты не будут

близки к вероятностям p

, и с ростом n величина χ

будет увеличиваться.

При фиксированном уровне значимости α будет фиксировано пороговое

число

(

)

)(r

1 α−

. Поэтому, увеличение n приведет к неравенству:

)(r

α−

χ>χ

, (8.3.4)

где

- выборочное значение статистики χ

, вычисленное по (8.3.2).

При реализации (8.3.4)

попадет в критическую область, и неверная ги-

потеза будет отвергнута.

Рис. 8.3.1. Критическая область критерия хи-квадрат.

Из этих рассуждений следует, что при сомнительной ситуации, когда

)(r

α−

χ≈χ

, следует увеличить объем выборки, например, в два раза, что-

бы проверяемое неравенство было более четким.

Замечание. Практика применения критерия χ

показывает, что если

для каких-либо подмножеств ∆

(i=1, 2, …, k) условие 5≥

⋅

pn не выпол-

няется, то следует объединить соседние подмножества (промежутки).

Это условие выдвигается требованием близости величин

pnn

⋅

−

(квадраты которых являются слагаемыми χ

) к нормальным с математиче-

ским ожиданием равным нулю и средним квадратическим отклонением

равным единице N(0, 1). Тогда случайная величина в формуле (8.3.2) будет

распределена по закону, близкому к хи-квадрат. Такая близость обеспечи-

вается достаточной численностью элементов в подмножествах ∆

152

Определение. Квантилью порядка d непрерывной случайной величи-

ны Х называется ее значение х

, являющееся корнем уравнения:

dxF

)(

(8.3.5)

Алгоритм проверки гипотезы

о законе распределения генеральной совокупности.

1. Выбирается уровень значимости α.

2. С помощью гипотетической функции распределения F(x) с числом

оцениваемых параметров l вычисляются оценки вероятностей

)(

XPp ∆∈= , i = 1, 2,…, k.

3. По таблице (Приложение 8.4) находится квантиль

(

)

)(r

α−

χ распреде-

ления хи-квадрат с r = k-l-1 степенями свободы порядка 1-α.

4. Находятся частоты n

попадания элементов в подмножества ∆

, и вы-

числяется выборочное значение статистики критерия хи-квадрат:

(

)

∑

⋅

⋅−

pnn

5. Производится сравнение

χ с квантилью

(

)

)(r

α−

χ .

Если

χ <

(

)

)(r

α−

χ , то гипотеза Н

принимается.

В противном случае гипотеза Н

отвергается.

Пример 8.3.1.

Произведено 50 измерений уровня радиации в помещении. Результа-

ты измерения (мкЗв/час) после их упорядочения в порядке возрастания

сведены в табл. 8.3.1.

Таблица 8.3.1.

Результаты измерений после их упорядочения.

0.10 0.11 0.12 0.12 0.12 0.12 0.12 0.13 0.14 0.14

0.15 0.15 0.16 0.17 0.17 0.17 0.17 0.18 0.18 0.18

0.18 0.19 0.19 0.19 0.20 0.20 0.20 0.20 0.20 0.20

0.20 0.21 0.21 0.21 0.21 0.22 0.22 0.22 0.22 0.22

0.22 0.23 0.23 0.23 0.24 0.24 0.24 0.25 0.25 0.29

Выдвигается гипотеза Н

о том, что распределение значений произ-

веденных измерений подчинено нормальному закону. Требуется подтвер-

дить или отвергнуть выдвинутую гипотезу.

Решение.

Представленные в табл. 8.3.1 данные представляют собой выборку

объемом n = 50 значений уровня радиации в помещении.

Определяем число k интервалов для группированного ряда:

()

интерваловnk 62.6)50ln(33.11ln33.11

≈

⋅

+=⋅+=

Определяем длину промежутков h:

153

03.0031.0

1.029.0

minmax

≈=

−

Составляем табл. 8.3.2, содержащую границы интервалов.

Таблица 8.3.2.

Границы промежутков выборки.

Границы интервалов №

промежутка

i-1

Число значений

в интервале, n

Средняя точка

промежутка

1 0.1 0.13 8 0.1150

2 0.13 0.16 5 0.1450

3 0.16 0.19 11 0.1750

4 0.19 0.21 11 0.2000

5 0.21 0.24 12 0.2250

6 0.24 0.29 3 0.2650

Сумма 50

Легко заметить, что значения границ определены прибавлением к

левому значению интервала величины h, например:

13.003.01.0

=+=+= haa

Рассчитываем выборочные числовые характеристики для выборки

табл. 8.3.1 с помощью группированного статистического ряда табл. 8.3.2.

Составим табл. 8.3.3, где z

– средняя точка i-го интервала.

Таблица 8.3.3.

Расчет первых двух выборочных моментов.

I n

)

⋅z

⋅(z

)

1 8 0.1150 0.0132 0.920 0.1058

2 5 0.1450 0.0210 0.725 0.1050

3 11 0.1750 0.0306 1.925 0.3368

4 11 0.2000 0.0400 2.200 0.4400

5 12 0.2250 0.0506 2.700 0.6075

6 3 0.2650 0.0702 0.795 0.2106

50 - - 9.265 1.8057

Используя данные табл. 8.3.3, находим выборочное среднее

, вы-

борочные дисперсию s

и среднее квадратическое отклонение s.

С помощью группированного статистического ряда можно ориенти-

ровочно определить выборочные моменты, поскольку группа элементов

выборки, входящих в промежуток ∆

может быть заменена средней точкой

, т.е. можно считать, что элемент z

встречается в выборке n

раз, или

имеет частоту n

, тогда:

∑

⋅⋅≈

iir

часмкЗв

aх

/1853.0

265.9

⋅

≈=

∑

154

0361.0

8057.1

⋅

∑

0018.00343.00361.0

=−=−= xas

042.00018.0

=== ss

мкЗв/час

Вычисляем выборочное значение статистики критерия хи-квадрат

(8.3.2), для чего составим табл. 8.3.4.

Таблица 8.3.4.

Вычисление

для проверки гипотезы о нормальном законе рас-

пределения измерений радиации в помещении.

Грани-

цы

i-1

−

i-1

)

-Ф

i-1

)

⋅p

-n⋅p

pnn

⋅

⋅−

)(

- ∞ - ∞

- 0.5

0.13

-2.1993 -0.4857

0.01430 0.715 7.285 74.225

0.13 -2.1993 -0.4857 2

0.16

-1.0657 -0.3554

0.13027 6.5135 - 1.5135 0.3517

0.16 -1.0657 -0.3554 3

0.19

0.06802 0.0279

0.38333 19.1665 - 8.1665 3.4795

0.19 0.06802 0.0279 4

0.21

0.82381 0.2939

0.26599 13.2995 - 2.2995 0.3975

0.21 0.82381 0.2939 5

0.24

1.95743 0.4750

0.18111 9.0555 2.9445 0.9574

0.24 1.95743 0.4750 6

∞

+ ∞

0.5

0.02500 1.250 1.7500 2.4500

50 1.00 50 0.0 81,8618

Число параметров, оцениваемых в нормальном законе распределения

равно l = 2, следовательно, число степеней свободы асимптотического хи-

квадрат распределения равно:

31261 =−−

−−= lkr

Выбираем уровень значимости α = 0.95, тогда квантиль хи-квадрат

распределения (Приложение 8.4) равен

81.7)3()(

05.0

−

χχ

. Сравнивая

на основе (8.3.4) выборочное значение

8618.81

с квантилью

)3(

05.0

делаем [поскольку

χ >

(

)

)(r

α−

χ ], вывод:

гипотеза Н

о нормальном законе распределения полученных при из-

мерениях значений уровня радиации в помещении отвергается.

155

8.4. Точность и надежность оценки вероятности реализации со-

бытия с помощью его относительной частоты

при большом объеме выборки.

Пусть р – вероятность реализации события А,

∗

- его относи-

тельная частота. Тогда, полагая:

(

)

∗∗

−⋅

⋅=

(8.4.1)

где: γ - надежность (вероятность), с которой доверительный интервал на-

крывает значение вероятности р реализации события,

−= 1

- уровень значимости;

- квантиль нормального распределения N(0, 1) порядка

;

ε - половина длины доверительного интервала.

Тогда:

(

)

γεε

=+<<−

∗∗

pppP

(8.4.2)

Пример 8.4.1.

Известен объем выборки n=550, задана требуемая надежность γ=0.95.

Необходимо построить доверительный интервал для вероятности с

помощью найденной по выборке р

= 0.3.

Решение

С помощью таблицы (Приложение 8.1) квантилей нормального рас-

пределения находим:

96.1

975.0

Определяем половину длины доверительного интервала:

0383.00195.096.1

550

7.03.0

975.0

=⋅=

⋅

⋅= u

Таким образом, значение искомой вероятности реализации события А

с надежностью γ = 0.95 находится в интервале [(р

- ε), (р

+ ε)]:

95.0)3385.02615.0()0385.03.00385.03.0( =

+<<− pPpP

8.5. Доверительный интервал для математического ожидания

нормальной генеральной совокупности.

Пусть по выборке объемом n из генеральной совокупности опреде-

лены выборочное среднее значение m

и выборочное среднее квадратиче-

ское отклонение s. Кроме того задана требуемая надежность γ.

156

Пусть также известно, что для выборки объема n из нормальной ге-

неральной совокупности случайная величина:

(

)

−

⋅−1

(8.5.1)

распределена по закону Стьюдента.

Здесь:

- выборочное среднее (найденное по выборке);

s – выборочное среднее квадратическое отклонение;

m – истинное значение математического ожидания генеральной

совокупности (измерений) при нормальном законе распределения слу-

чайной величины;

n – объем выборки.

Вероятность того, что математическое ожидание m входит в ин-

тервал, ограниченный значениями (8.5.1) равна:

∫

−

−−

−=

xFdttf 12

)()(

(8.5.2)

где f

n-1

(x) – плотность распределения вероятностей Стьюдента (функ-

ция четная);

n-1

(x) – функция распределения случайной величины по закону

Стьюдента с n-1 степенями свободы.

По таблице распределения Стьюдента (Приложение 8.2) с n-1 степе-

нями свободы находим квантиль порядка

и получаем искомый дове-

рительный интервал для m:

γγ

⎟

⎠

⎞

⎜

⎝

⎛

−

−⋅

+<<

−

−⋅

−

)1(

nts

где W(A) – вероятность реализации события А.

Пример 8.5.1.

Произведено n=30 измерений концентрации газа в резервуаре перед

его очисткой. Сделано предположение о нормальном распределении ре-

зультатов измерений в генеральной совокупности. Выборочное среднее и

выборочное среднее квадратическое отклонение соответственно равны:

8.0=x

2.0

Требуется с достоверностью 0.95 определить интервал значений ис-

тинного математического ожидания концентрации газа в резервуаре.

Решение.

По таблице распределения Стьюдента (Приложение 8.2) находим

квантиль порядка 0.975 для 29 степеней свободы:

157

045.2)29()130(

975.0

95.01

−

Тогда значение искомого математического ожидания с требуемой на-

дежностью находится в интервале:

045.22.0

8.0

045.22.0

8.0

⋅

+<<

⋅

− m

Или вероятность того, что

876.0724.0

равна 0.95.

8.6. Доверительный интервал для среднего квадратического отклоне-

ния нормальной генеральной совокупности.

Если произведена выборка объемом n из генеральной совокупности,

где по предположению случайная величина распределена по нормальному

закону, вычислено выборочное среднее квадратическое отклонение s и за-

дана требуемая надежность γ, то соответствующий доверительный интер-

вал, в котором содержится среднее квадратическое отклонение

σ, может

быть определен с помощью χ

– распределения (Приложение 8.4) с n-1

степенями свободы порядков (1-γ)/2 и (1+γ)/2:

γγ

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−

⋅

−+

)1()1(

(8.6.1)

Замечание. В знаменателе под знаком радикала не произведение

на (n-1), а

с (n-1) степенями свободы.

Пример 8.6.1.

По исходным данным примера 8.5.1 найти истинное среднее квадрати-

ческое отклонение концентрации газа в резервуаре.

По таблице распределения χ

находим соответствующие квантили:

93.15)29()130(

025.0

95.01

==−

−

χχ

95.46)29()130(

975.0

95.01

==−

χχ

Вычисляется доверительный интервал:

()

95.0274.0159.0

93.15

302.0

95.46

302.0

=<<=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

σσ

где W(А) – вероятность реализации события А.

158

8.7. Проверка статистических гипотез.

Статистической гипотезой называется предположение о виде или

свойствах генерального или выборочного распределений, которое можно

проверить статистическими методами на основе имеющейся выборки.

Постановка задачи.

Изучаются две генеральные совокупности случайных величин X и Y,

распределенных по нормальному закону:

,...,,

21 n

xxx

- выборка объемом n

из первой совокупности,

,...,,

21 n

yyy

- выборка объемом n

из второй совокупности.

Обе выборки получены независимо одна от другой.

Требуется проверить гипотезу о равенстве дисперсий и о равенстве

математических ожиданий.

Алгоритм проверки гипотезы о равенстве дисперсий.

1. Вычисляются выборочные математические ожидания

2. Вычисляются несмещенные оценки дисперсий:

()

∑

−⋅

−

()

∑

−⋅

−

3. В качестве статистического критерия выбирается отношение:

()

,min

),(max

Это отношение распределено по закону Фишера с числом степеней

свободы:

= (n

-1) и k

=(n

-1) , если

ss >

= (n

-1) и k

=(n

-1) , если

ss <

Закон Фишера распределения случайных величин обозначается F(k

, k

4. Выбирается уровень значимости α.

5. По таблице распределения Фишера находится квантиль F

1-α

6. Делается вывод о подтверждении или отвержении гипотезы на

основании сравнения критерия F

и квантиля F

1-α

Если F

< F

1-α

) гипотеза о равенстве дисперсий принимается

с вероятностью 1-α,

Если F

≥ F

1-α

) гипотеза о равенстве дисперсий отвергается

с вероятностью 1-α.

Пример 8.7.1.

Пусть n

=16, 23.1

s ; n

=20, 97.0

s ; α = 0.05.

Требуется проверить предположение о равенстве дисперсий этих

выборок.

159

Решение.

Числа свободы k

=15, k

=19.

Значение статистического критерия:

27.1

97.0

23.1

По таблице распределения Фишера находим квантиль F

1-α

, k

) = F

0.95

(15, 19) = 2.23

Поскольку выполняется неравенство:

< F

1-α

) – гипотеза о равенстве дисперсий принимается.

8.8. Проверка гипотезы о равенстве математических ожиданий

двух нормальных генеральных совокупностей.

Имеются две независимые выборки из двух генеральных совокупно-

стей с нормальным распределением случайной величины:

,...,,

21 n

xxx

- выборка объемом m из первой совокупности,

,...,,

21 n

yyy

- выборка объемом n из второй совокупности.

По этим выборкам находятся выборочные средние и выборочные

дисперсии:

∑∑

⋅=⋅=

() ()

∑∑

−⋅

−

=−⋅

−

)1(

sxx

Пусть предварительно была проверена гипотеза о равенстве диспер-

сий генеральных совокупностей и сделан вывод об их равенстве:

σσσ

Алгоритм решение задачи проверки равенства математических ожи-

даний нормальных генеральных совокупностей.

1. Принимается статистика критерия:

2121

)2(

nnnn

snsn

−+⋅⋅

⋅

⋅+⋅

−

(8.8.1)

Доказано, что эта статистика Т распределена по закону Стьюдента с

числом степеней свободы k:

k = n

+ n

– 2 (8.8.2)

2. Назначается уровень значимости α.

3. По таблице распределения Стьюдента находится квантиль:

160

)2(

−

nnt

(8.8.3)

4. Производится сравнение модуля Т

)2(

−

nnt

Гипотеза о равенстве математических ожиданий принимается, если:

)2(

−+<

−

nntT

(8.8.4)

Гипотеза о равенстве математических ожиданий отвергается, если:

)2(

−+≥

−

nntT

(8.8.5)

Принятие или отвержение гипотез производится с достоверностью γ = 1-α.

Пример 8.8.1.

Требуется сравнить содержание вредных примесей в воде (эффек-

тивности предпринятых мер повышения качества воды) технологического

колодца с надежностью γ = 0.95 (уровнем значимости α= 0.05).

Произведено две серии независимых измерений, Распределенных по

нормальному закону. Первая серия (х) объемом n

= 19 измерений произве-

дена до применения мер очистки воды, вторая (y) объемом n

= 21 измере-

ние - после:

(Х): (0.11, 0.13, 0.22, 0.17, 0.19, 0.23, 0.25, 0.14, 0.18, 0.11, 0.15, 0.17, 0.10,

0.24, 0.16, 0.19, 0.21, 0.24, 0.20);

(Y): (0.19, 0.17, 0.10, 0.10, 0.20, 0.11, 0.15, 0.15, 0.19, 0.25, 0.21, 0.17, 0.10,

0.14, 0.18, 0.20, 0.21, 0.17, 0.11, 0.16, 0.19)

Решение

1. Производятся непосредственные вычисления выборочных средних

значений и выборочных дисперсий по выборкам:

001786.0002192.0

164286.0;178421.0

2. Вычисляется отношение Фишера:

227.1

001786.0

002192.0

3. По таблице распределения Фишера находится квантиль:

17.2)20,18()1,1(),(

95.0211211

−

−−

FnnFkkF

αα

Производится сравнение статистики критерия (отношения Фишера)

со значением найденного квантиля.

Поскольку 1.227 < 2.17, то можно сделать вывод о том, что с вероят-

ностью 0.95 обе выборки принадлежат генеральным совокупностям с рав-

ными дисперсиями.