Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

ть—средняя квадратическая ошибка исходной (ба-

зисной) стороны;

ль — средняя квадритическая ошибка связующей сто-

роны в треугольнике с номером k\

—продольный сдвиг ряда;

—поперечный сдвиг ряда;

—средняя квадратическая ошибка азимута диаго*

нали ряда;

M=ym

L+w

g—средняя квадратическая ошибка положения ко-

нечной точки ряда относительно его начала.

Средняя квадратическая ошибка длины связу-

ющей стороны ряда триангуляции. При уравнивании

ряда триангуляции (см. рис. 21) по направлениям за условия фи-

гур среднюю квадратическую ошибку длины связующей стороны

в треугольнике с номером k найдем по формуле

i a

-^y^gMi+ctg**! + ctg^ctgS,) (3.20)

s*k Ь

^ 3 p»

£-1

или в логарифмической форме

т\

lg b

e m%

+ •

где

/Р

8/г

—обратный вес связующей стороны, вычисляемый по

формуле

i = l

в которой для каждого треугольника принято

Я = б

л + б

в + б

. (3.23)

Здесь 8а, бв—изменения логарифмов синусов связующих уг-

лов при изменении этих углов на одну секунду, выраженные в еди-

ницах шестого знака логарифма:

АМ0«

б—р— ctgi4 = 2,105ctg

Л;

(3.24)

М = 0,43429 — модуль неперовых логарифмов; ошибки логарифмов

связующих сторон (m\gs

) выражаются также в единицах шестого

знака логарифма.

К относительной ошибке стороны переходят по формуле

mjg

М-10°

434 300:mj

g s

e (3

25)

Обратный вес последней связующей стороны звена триангуля-

ции принято называть обратным весом звена.

Если в ряде триангуляции кроме треугольников имеются гео-

дезические четырехугольники и центральные системы, то обрат-

ный вес связующей стороны каждого треугольника в таких фигу-

рах вычисляется по формуле проф. В. А. Магницкого

1 4 D —

(с

—

)

= — Sr^R. (3.26)

где D — число направлений в фигуре без двух; с

—

число условных

уравнений в фигуре при уравнивании ее по направлениям; с

—

число условных уравнений в фигуре после превращения ее в про-

стую цепочку треугольников путем исключения избыточных сто-

рон.

В отдельно взятом треугольнике с

— со,

и потому коэффициент

при R равен -j. Для треугольника, входящего в геодезический че-

тырехугольник или центральную систему, коэффициент при R ра-

вен На практике его принимают для таких треугольников

равным единице и при вычислении обратного веса звена триангу-

ляции берут те треугольники, которые дают наименьшую величину

обратного веса.

В случае когда ряд состоит из равносторонних треугольников

(Л = В = С = 60°), формула (3.20) принимает вид

*k ,/ m

** у Ь*

2 т'->

+ -* —Л, (3.27)

где k — номер треугольника.

Средняя квадратическая ошибка азимута свя-

зующей стороны ряда триангуляции. Азимуты в ря-

дах триангуляции при составлении азимутальных условий пере-

дают по ходовой линии, показанной на рис. 21 пунктиром. Сред-

няя квадратическая ошибка азимута связующей стороны в тре-

угольнике с номером k при измерении и уравнивании углов за ус-

ловия фигур вычисляется по формуле

та

= т*

+ Ы'

, (3.28)

а при уравнивании измеренных направлений — по формуле

2k +

т*

+ КГ"

™

* (3-29)

Продольный и поперечный сдвиг ряда триан-

гуляции. В результате влияния ошибок измерений конечная

точка уравненного ряда триангуляции смещается вдоль направ-

ления ряда на среднюю квадратическую величину т

, называе-

мую продольным сдвигом ряда, и поперек направления ряда на

среднюю квадратическую величину m

, называемую поперечным

сдвигом ряда (см. рис. 21).

Продольный сдвиг свободного ряда (см. рис. 21), состоящего

из равносторонних треугольников и уравненного за условия фигур

по углам или направлениям, может быть вычислен по формуле

, 1 f

4л

±3/г + 5 т

нЪ

-р"' (

где знак минус перед 3п берется при нечетном и знак плюс — при

четном числе N треугольников в ряде.

Поперечный сдвиг свободного ряда из равносторонних треуголь-

ников при уравнивании его за условия фигур по направлениям вы-

числяется по формулам:

при нечетном числе N треугольников в ряде

l/"

•

„

пЧп + 3

при четном числе N треугольников в ряде

(3.31)

-fV

тГ* 2п

Ъп

+ 5

+ ~J5 „ - (3.32)

В формулах (3.30) — (3.32) через п обозначено число проме-

жуточных сторон в диагонали ряда, отсчитываемых по одному его

краю.

Вычислив продольный сдвиг ряда m

, найдем относительную

ошибку длины диагонали ряда m

Средняя квадратическая ошибка азимута диагонали ряда на-

ходится по формуле

Средняя квадратическая ошибка положения конечной точки

ряда относительно начальной равна

М » /««

+ т\. (3.34)

Для примера по формулам (3.27) — (3.34) выполним оценку

точности элементов свободного ряда триангуляции из равносто-

ронних треугольников, уравненного по направлениям за условия

фигур. В этом ряде: L = 176 км,

= 22 км, N = k= 16,

п*=

8, /п=0,7",

~ =

:400

ООО,

= 1,1". Результаты сведем в табл. 5.

2. Оценка точности элементов ряда триангуляции из равносто-

ронних треугольников с базисами и азимутами на его концах.

Пусть дан ряд триангуляции из равносторонних треугольников с

базисными сторонами и азимутами Лапласа на его концах (рис.

22), уравненный по направлениям за условия фигур, базисов и

азимутов.

В таком ряде средняя квадратическая ошибка в логарифме

связующей стороны вычисляется по формуле

Г т\гь , « „2 (N-k)k

les

=y —2 b 3,15m д?

Щёв

ЛМО

•

(3.35)

Средняя квадратическая ошибка азимута связующей стороны

находится по формуле

«a

У 2+25 [(Ы+

)- 5^

+I2

J- (3.36)

Продольный и поперечный сдвиги ряда равны

£ 1 f tn*b 2/г

— Зп + 10 т"

— <

з7

1 /л,* а.

Па + 2/г+12

л^ ^

В формулах (3.35) — (3.38) N — число треугольников в ряде;

k — номер треугольника, в котором расположена оцениваемая сто-

Таблица 5

Оцениваемый элемент ряда триангуляции

Формула

Ошибка

Средняя квадратическая ошибка последней связую-

щей стороны ряда:

(3.27)

0,25 м

а) абсолютная

(3.27)

0,25 м

б) относительная

(3.27)

1:88

ООО

Средняя квадратическая ошибка азимута последней

(3.29)

связующей стороны ряда

(3.29)

1J"

Продольный сдвиг ряда

(3.30)

1,27 м

Поперечный сдвиг ряда

(3.32)

1,18 м

Относительная ошибка длины диагонали ряда

1:139

ООО

Средняя квадратическая ошибка азимута диагонали

ряда (3.33)

1,4"

Средняя квадратическая ошибка положения конечной

(3.34) 1,73 м точки ряда (3.34) 1,73 м

рона; п — число промежуточных сторон в диагонали ряда L, от-

считываемых по одному его краю; т!\ т

, ть/Ь

—

средние квадра-

тические ошибки измерения углов, азимутов Лапласа и базисных

сторон соответственно. Ошибки в логарифме базисных {m\

) и

связующих сторон (mjg,c) выражаются в единицах шестого знака

логарифма.

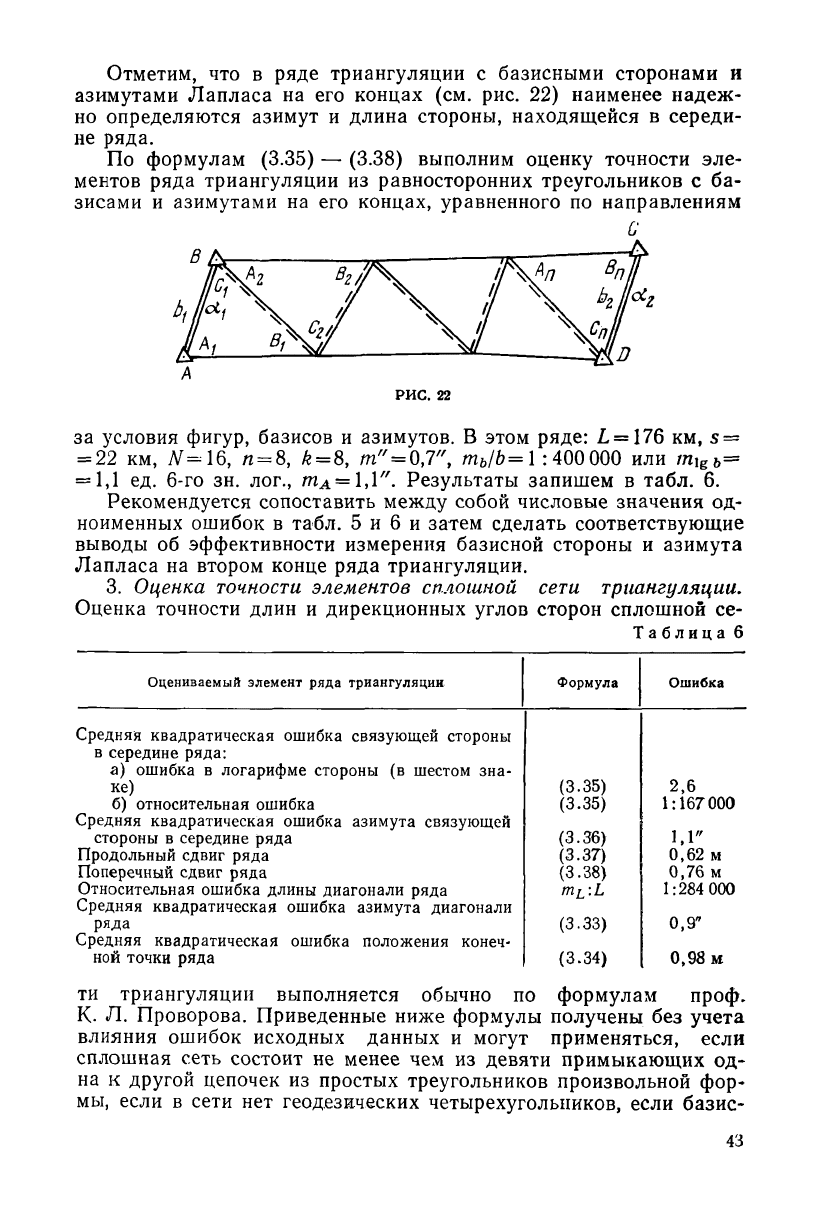
Отметим, что в ряде триангуляции с базисными сторонами и

азимутами Лапласа на его концах (см. рис. 22) наименее надеж-

но определяются азимут и длина стороны, находящейся в середи-

не ряда.

По формулам (3.35) — (3.38) выполним оценку точности эле-

ментов ряда триангуляции из равносторонних треугольников с ба-

зисами и азимутами на его концах, уравненного по направлениям

за условия фигур, базисов и азимутов. В этом ряде: L = 176 км, s==

= 22 км, 16,

= 8, 6 = 8, m" = 0,7", m

/b=

:400

ООО

или mi

= 1,1 ед. 6-го зн. лог., /Па = 1,1". Результаты запишем в табл. 6.

Рекомендуется сопоставить между собой числовые значения од-

ноименных ошибок в табл. 5 и 6 и затем сделать соответствующие

выводы об эффективности измерения базисной стороны и азимута

Лапласа на втором конце ряда триангуляции.

3. Оценка точности элементов сплошной сети триангуляции.

Оценка точности длин и дирекционных углов сторон сплошной се-

Таблица б

Оцениваемый элемент ряда триангуляции

Формула

Ошибка

(3.35)

2 6

1:167

ООО

(3.36)

(3.37)

(3.38)

1,1"

0,62 м

0,76 м

1:284 000

(3.33)

0,9"

(3.34)

0,98 м

формулам проф.

Средняя квадратическая ошибка связующей стороны

в середине ряда:

а) ошибка в логарифме стороны (в шестом зна-

ке)

б) относительная ошибка

Средняя квадратическая ошибка азимута связующей

стороны в середине ряда

Продольный сдвиг ряда

Поперечный сдвиг ряда

Относительная ошибка длины диагонали ряда

Средняя квадратическая ошибка азимута диагонали

ряда

Средняя квадратическая ошибка положения конеч-

ной точки ряда

ти триангуляции выполняется обычно по

влияния ошибок исходных данных и могут применяться, если

сплошная сеть состоит не менее чем из девяти примыкающих од-

на к другой цепочек из простых треугольников произвольной фор-

мы, если в сети нет геодезических четырехугольников, если базис-

ные стороны с азимутами Лапласа размещаются через 10—25 тре-

угольников (10^Л^25), а сеть уравнена по углам как свободная

за условия фигур, горизонтов, полюсов, дирекционных углов и ба-

зисов.

В такой сети триангуляции точность определения дирекцион-

ных углов и длин сторон треугольников, удаленных от границы се-

ти не менее чем на 4—5 треугольников, практически одинакова во

всех ее частях.

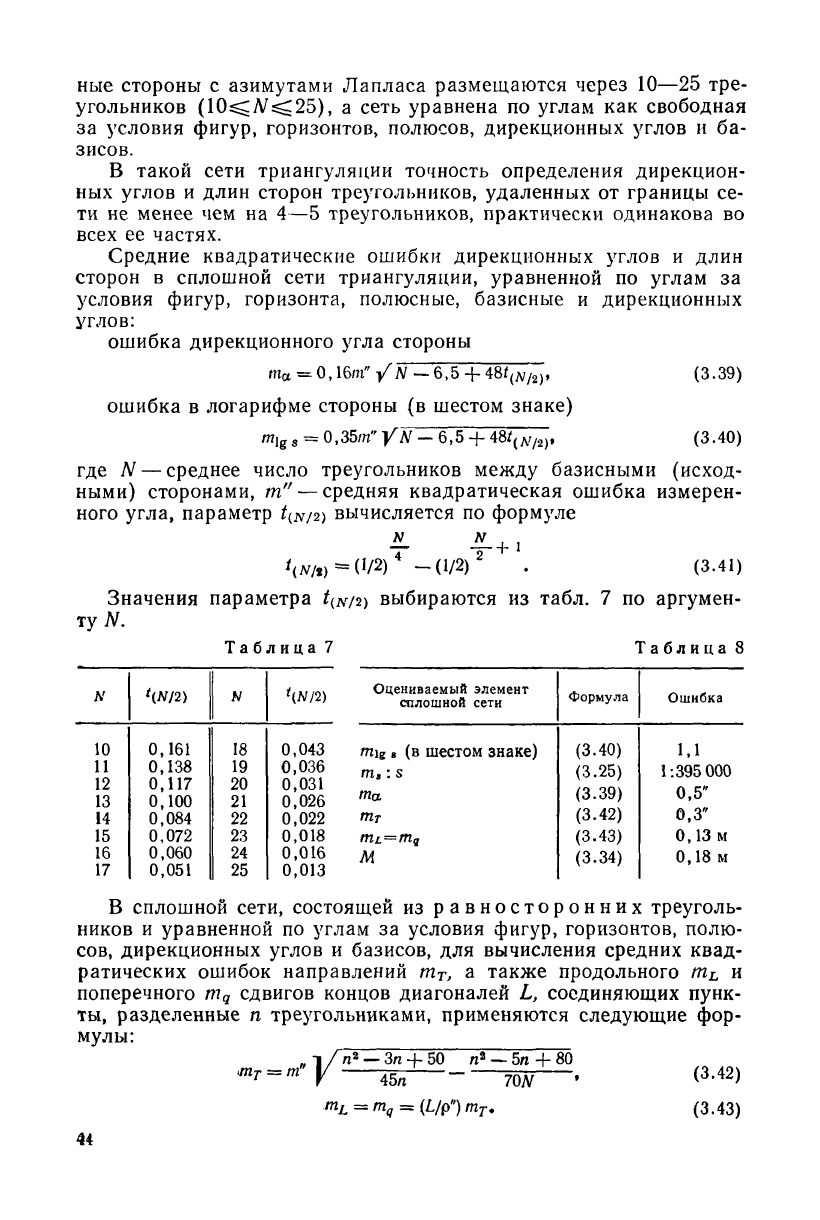
Средние квадратические ошибки дирекционных углов и длин

сторон в сплошной сети триангуляции, уравненной по углам за

условия фигур, горизонта, полюсные, базисные и дирекционных

углов:

ошибка дирекционного угла стороны

та = 0,16/n" /N

—

6,5 + Щм

/2)9

(3.39)

ошибка в логарифме стороны (в шестом знаке)

lgs

= 0,35/77" /ЛГ-6,5 + 48/

(

72)

, (3.40)

где N — среднее число треугольников между базисными (исход-

ными) сторонами, т"— средняя квадратическая ошибка измерен-

ного угла, параметр t^j2) вычисляется по формуле

It iL

'(AW~(l/2)

-(1/2)

. (3.41)

Значения параметра t

{N/2)

выбираются из табл. 7 по аргумен-

ту N.

Таблица 7 ТаблицаЗ

N '(JV/2) N

'(N/2)

0,161 18 0,043

11 0,138

0,036

0,117

0,031

0,100 21

0,026

0,084 22

0,022

0,072

23 0,018

0,060

0,016

0,051

0,013

Оцениваемый элемент

сплошной сети

Формула

Ошибка

mig

(в шестом знаке)

(3.40)

1,1

: s

(3.25)

1:395

000

(3.39) 0,5"

Шт

(3.42)

0,3"

IflL

Tflq

(3.43)

0,13 м

(3.34)

0,18 м

В сплошной сети, состоящей из равносторонних треуголь-

ников и уравненной по углам за условия фигур, горизонтов, полю-

сов, дирекционных углов и базисов, для вычисления средних квад-

ратических ошибок направлений т

Т>

а также продольного m

поперечного m

сдвигов концов диагоналей L, соединяющих пунк-

ты, разделенные п треугольниками, применяются следующие фор-

мулы:

tiif

_ sn + 50 n

—

5n + 80

45n 70N

L = = (W) Щ*

(3.42)

(3.43)

По формулам (3.39) — (3.43) вычислены средние квадратиче-

ские ошибки элементов сплошной сети триангуляции 2 класса при

N = 16, т" = 0,9", п= 14, 1 = 88 км. Результаты приведены в

табл. 8.

Необходимо обратить внимание на то обстоятельство, что в се-

ти триангуляции 2 класса, уравненной внутри полигона 1 класса

за все возникающие условия, происходят заметные искажения

уравненных элементов сети 2 класса из-за влияния ошибок исход-

ных данных, т. е. ошибок в координатах пунктов, длинах и дирек-

ционных углах сторон 1 класса. Эти искажения наибольшей вели-

чины достигают на краях сети 2 класса (в местах соединения пунк-

тов 1 и 2 классов) и нелинейно уменьшаются в направлении к цен-

тральной части сплошной сети, где они становятся незначитель-

ными.

От этого недостатка в принципе можно избавиться, если сети 1

и 2 классов уравнять совместно, рассматривая их как единую по

построению сплошную астрономо-геодезическую сеть (без подраз-

деления на классы).

§ 10. Оценка точности элементов звена

полигонометрии 1 класса

Будем полагать, что полигонометрический ход 1 класса явля-

ется вытянутым, на его концах определены азимуты Лапласа и что

уравнен он за условие азимутов (дирекционных углов).

Средняя квадратическая ошибка азимута любой стороны звена

вычисляется по формуле

2 k (п

1 —

Н = У +

п+1 '

44)

Продольный и поперечный сдвиги конечной точки звена отно-

сительно начальной равны

Ytn*

n + т*

, (3.45)

(3.46,

В формулах (3.44) — (3.46) п — число всех сторон в звене по-

лигонометрии; k — номер стороны звена; L = ns — длина диагона-

ли звена; т", m

, tn

— соответственно средние квадратические

ошибок и измерения углов, длин сторон и азимутов Лапласа; т

—

систематическая ошибка измерения расстояний светодальномером

из-за неточного знания скорости распространения света в атмо-

сфере (m

»s- 10~

По формулам (3.44) — (3.46) произведем оценку точности эле-

ментов вытянутого полигонометрического звена, в котором L =

= 176 км,

= 22 км,

/г

= 8, 6 = 4, m" = 0,7"; m

/s=

:300

ООО;

-10~

, т

= \>\". Результаты сведем в табл. 9.

Таблица 9

Оценивае-

мый элемент

звена

Формула

Ошибка

Оценивае-

мый элемент

звена

Формула

Ошибка

(3.44)

1,3"

1:652 000

™L

(3.45) 0,27 м

(3.33)

1,0"

tTlq

(3.46)

0,88 м

(3.34)

0,92 м

§ 11. Оценка точности построения рядов

и сплошных сетей трилатерации

1. Точность определения углов в треугольнике с измеренными

сторонами. В треугольнике ABC с измеренными сторонами а, Ь, с

(рис. 23) средняя квадратическая ошибка любого угла, например

д угла А, вычисленного по теореме косинуса уг-

ла, может быть найдена по формуле

•

(т

cos

+ т

cos

В), (3.47)

где h

— высота треугольника, опущенная из

вершины угла А на противолежащую сторону:

sin

= bsm С, (3.48)

где т

ау

ntby т

— средние квадратические

ошибки измерения сторон.

В равностороннем треугольнике (a=b

—

c=s) при равноточных

измерениях длин сторон m

= m

средняя квадратическая

ошибка определения любого угла р=А,

В>

С равна

mfi*=*(m

/s)p*V2.

(3.49)

2. Оценка точности элементов ряда трилатерации. Приведем

формулы С. А. Бутлера для оценки точности элементов ряда три-

латерации из равносторонних треугольников, уравненного за ус-

ловие азимутов, определенных на обоих концах ряда:

средняя квадратическая ошибка азимута связующей стороны

ряда

*А . ±

-V 2+3

Ш'

с2

{N-k)k

(3.50)

продольный сдвиг ряда

-W-

л/

— 1

(3.51)

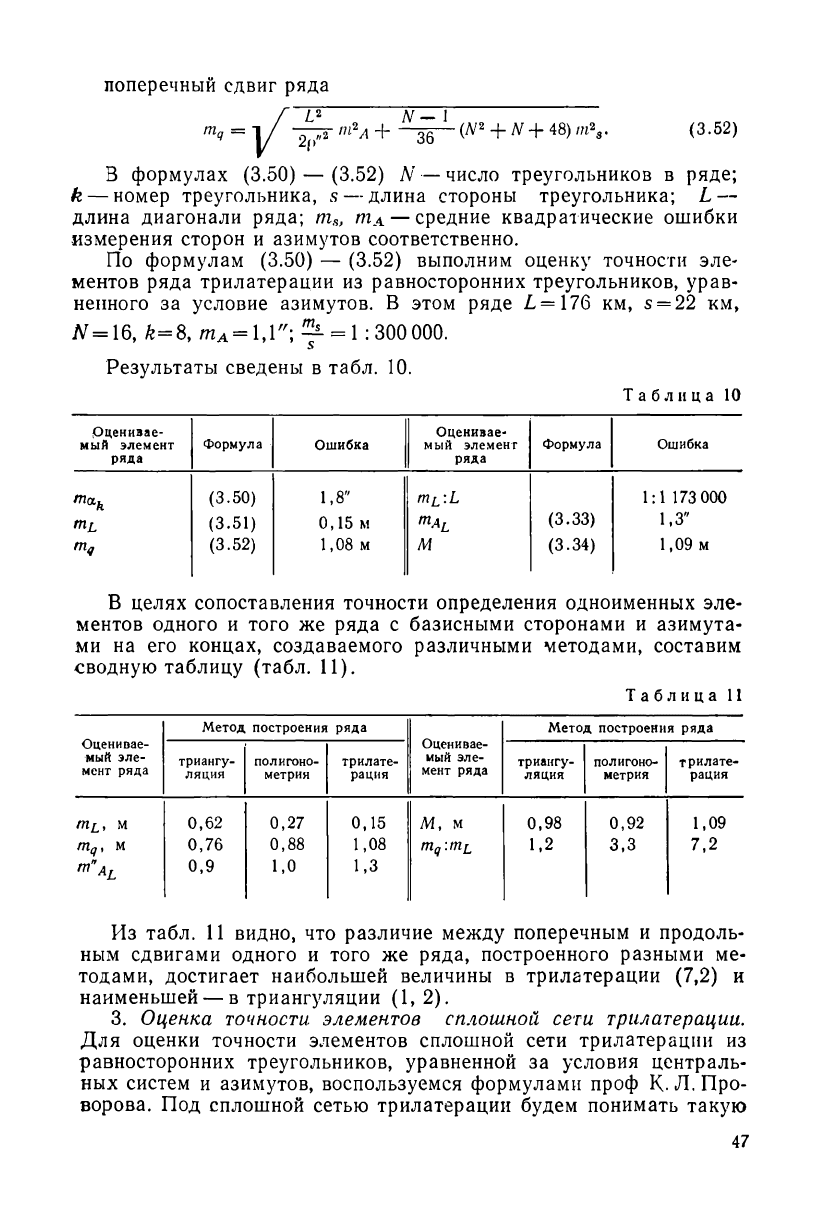
поперечный сдвиг ряда

mq =

]/ + (3.52)

В формулах (3.50) — (3.52) N — число треугольников в ряде;

k — номер треугольника, s— длина стороны треугольника; L —

длина диагонали ряда; m

— средние квадратические ошибки

измерения сторон и азимутов соответственно.

По формулам (3.50) — (3.52) выполним оценку точности эле-

ментов ряда трилатерации из равносторонних треугольников, урав-

ненного за условие азимутов. В этом ряде L= 176 км, s = 22 км,

N = 16, k=8, т

= 1,1"; у- =

: 300

ООО.

Результаты сведены в табл. 10.

Таблица 10

Оценивае-

мый элемент

ряда

Формула

Ошибка

Оценивав'

мый элемент

ряда

Формула

Ошибка

(3.50) 1,8"

1:1

173

000

(3.51)

0,15 м

(3.33)

1,3"

trig

(3.52)

1,08 м М (3.34) 1,09 м

В целях сопоставления точности определения одноименных эле-

ментов одного и того же ряда с базисными сторонами и азимута-

ми на его концах, создаваемого различными методами, составим

сводную таблицу (табл. И).

Таблица 11

Оценивае-

мый эле-

мент ряда

Метод построения ряда

Оценивае-

мый эле-

мент ряда

Метод построения ряда

Оценивае-

мый эле-

мент ряда

триангу-

ляция

полигоно-

метрии

трилате-

рации

Оценивае-

мый эле-

мент ряда

триангу-

ляция

полигоно-

метрия

т рилате-

рация

, м

0,62

0,27 0,15 M

М 0,98

0,92 1,09

, м 0,76

0,88 1,08

\tn

1,2

3,3

7,2

0,9

1,0 1,3

Из табл. И видно, что различие между поперечным и продоль-

ным сдвигами одного и того же ряда, построенного разными ме-

тодами, достигает наибольшей величины в трилатерации (7,2) и

наименьшей — в триангуляции (1, 2).

3. Оценка точности элементов сплошной сети трилатерации.

Для оценки точности элементов сплошной сети трилатерации из

равносторонних треугольников, уравненной за условия централь-

ных систем и азимутов, воспользуемся формулами проф К. Л.Про-

ворова. Под сплошной сетью трилатерации будем понимать такую

же по построению сеть, как сеть триангуляции 2 класса с опреде-

ленными в ней азимутами Лапласа.

Средние квадратические ошибки относительного положения

смежных пунктов:

а) продольный сдвиг конца стороны

ав0,83/п

; (3*53)

б) поперечный сдвиг конца стороны

= 1,20m,; (3-54)

в) общий сдвиг конечной точки стороны относительно ее на-

чала

и = ут\ + m

= 1,43m

; (3.55)

г) ошибка уравненного угла треугольника

т,

= 1,25 р". (3.56)

Средние квадратические ошибки элементов диагонали, соеди-

няющей пункты, разделенные рядом треугольников:

а) продольный сдвиг конца диагонали

l/ (N + J5) (£+11)

ь=т* У ю (А/+ 25)

;

б) поперечный сдвиг конца диагонали

(3.58)

(N + 15) (5ft

+ 12k + 8)

30 (N + 25)

;

в) ошибка направления диагонали

= (m

/L) р";

г) ошибка положения конечной точки диагонали относительно

ее начала

м = Vm*L + m

В формулах (3.53) — (3.58) m

— средняя квадратическая ошиб-

ка измерения сторон; N — число треугольников в цепочке между

исходными азимутами (по кратчайшему пути); k — число тре-

угольников в цепи между конечными пунктами оцениваемой диа-

гонали L.

По формулам (3.53) — (3.58) выполнена оценка точности эле-

ментов сплошной сети трилатерации из равносторонних треуголь-

ников, уравненной за условия центральных систем и азимутов.

В примере N= 16, £ = 8, m

/s =

:300

ООО,

5=11 км, /,=88 км. Ре-

зультаты сведены в табл. 12.

Из табл. 8 и 12 видно, что поперечный и продольный сдвиги

концов сторон в сплошной сети триангуляции одинаковы, в то

время как в сплошной сети трилатерации поперечный сдвиг в три

раза больше продольного.