Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

§ 38. Составление и решение нормальных уравнений

коррелат. Вычисление поправок направлений

Систему условных уравнений и весовой функции, которые при-

ведены в табл. 42, запишем в матричной форме

AV+W = 0, (8.11)

где А — прямоугольная матрица коэффициентов условных уравне-

ний и весовой функции, V— вектор-столбец поправок измеренных

с весами р направлений, W — вектор-столбец свободных членов

условных уравнений.

От уравнений поправок (8.11) перейдем к системе нормальных

уравнений коррелат

ACA*K+W = 0, (8.12)

где С — диагональная матрица обратных весов измеренных

направлений, Л*— транспонированная по отношению к А матрица

коэффициентов условных уравнений, К—вектор-столбец коррелат

нормальных уравнений; остальные обозначения указаны выше.

Нормальные уравнения перепишем в виде

NK+W = 0, (8.13)

где N — квадратная матрица коэффициентов нормальных уравне-

ний,

N =

АСА*

...а

2Г

J, (8.14)

* =

где г — число условных уравнений.

При равноточных измерениях направлений С = £, где Е — еди-

ничная матрица, и поэтому

N = АА*. (8.15)

Умножив уравнение (8.13) слева на матрицу = получим

вектор К искомых коррелат

К = —QW, (8.16)

где Q — матрица весовых коэффициентов, обратная к матрице N

коэффициентов нормальных уравнений,

/Qu Qia-..Qir\

Q = N-1 = j Q

...Q

j. (8.17)

\Qr

' Qra'.-'.Qrr/

Вектор поправок измеренных направлений найдем по формуле

V = CA*K (8.18)

119

12- •

•<*ir\

,а

2Г

Г2

rr /

/ щ

j ^2

\ w

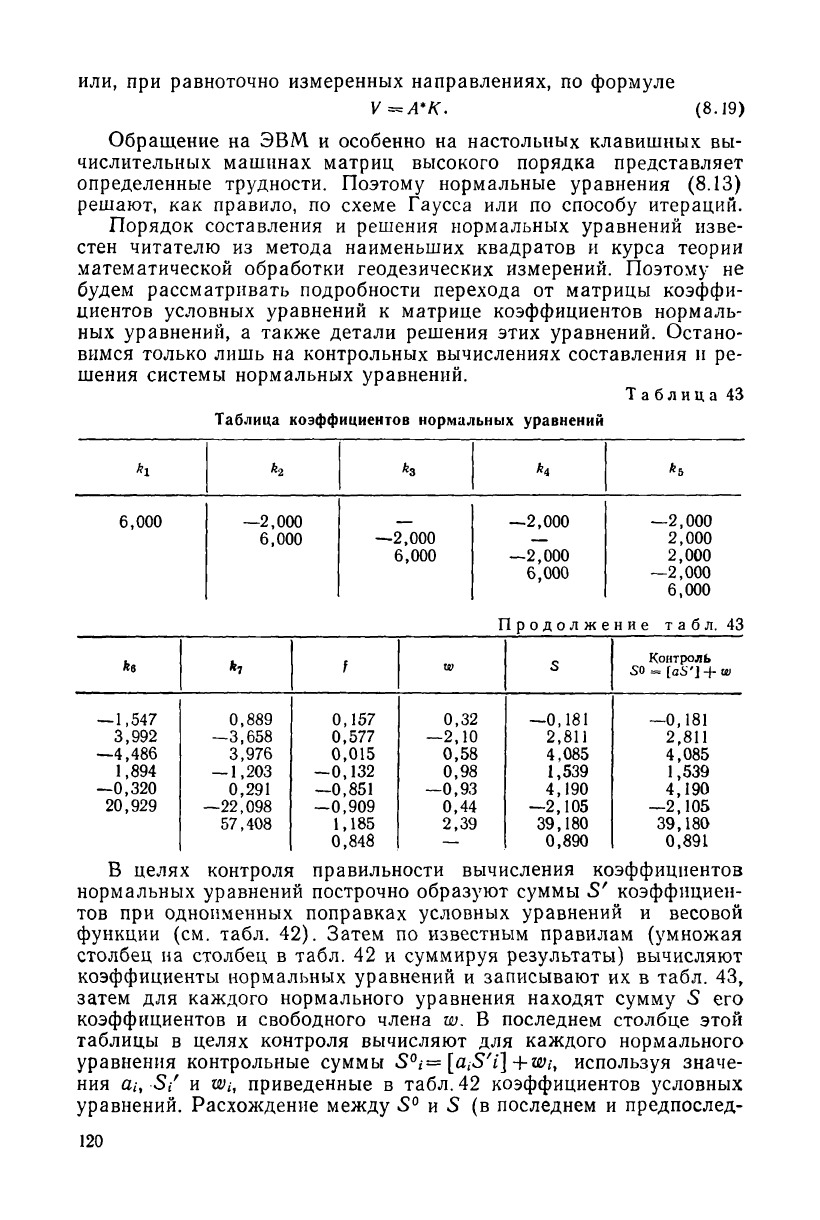
или, при равноточно измеренных направлениях, по формуле

V^A*K. (8.19)

Обращение на ЭВМ и особенно на настольных клавишных вы-

числительных машинах матриц высокого порядка представляет

определенные трудности. Поэтому нормальные уравнения (8.13)

решают, как правило, по схеме Гаусса или по способу итераций.

Порядок составления и решения нормальных уравнений изве-

стен читателю из метода наименьших квадратов и курса теории

математической обработки геодезических измерений. Поэтому не

будем рассматривать подробности перехода от матрицы коэффи-

циентов условных уравнений к матрице коэффициентов нормаль-

ных уравнений, а также детали решения этих уравнений. Остано-

вимся только лишь на контрольных вычислениях составления и ре-

шения системы нормальных уравнений.

Таблица 43

Таблица коэффициентов нормальных уравнений

*з

6,000

—2,000

6,000

—2,000

—

2,000

6,000

—2,000

2,000

6,000

—2,000

6,000

Продолжение табл. 43

fee

w s

Контроль

50 = [aS'J4-

—1,547

0,889

0,157

0,32

—0,181

3,992

-3,658

0,577

—2,10 2,811

2,811

—4,486

3,976

0,015 0,58

4,085 4,085

1,894

—

1,203

-0,132

0,98 1,539 1,539

—0,320

0,291

—0,851

—0,93

4,190

20,929

—22,098

-0,909

0,44

—2,105

57,408

1,185

2,39

39,180

0,848

—

0,890

0,891

В целях контроля правильности вычисления коэффициентов

нормальных уравнений построчно образуют суммы S' коэффициен-

тов при одноименных поправках условных уравнений и весовой

функции (см. табл. 42). Затем по известным правилам (умножая

столбец на столбец в табл. 42 и суммируя результаты) вычисляют

коэффициенты нормальных уравнений и записывают их в табл. 43,

затем для каждого нормального уравнения находят сумму 5 его

коэффициентов и свободного члена w. В последнем столбце этой

таблицы в целях контроля вычисляют для каждого нормального

уравнения контрольные суммы [a

S'/] +wi

используя значе-

ния а/, -Si' и Wi, приведенные в табл. 42 коэффициентов условных

уравнений. Расхождение между 5° и 5 (в последнем и предпослед-

120

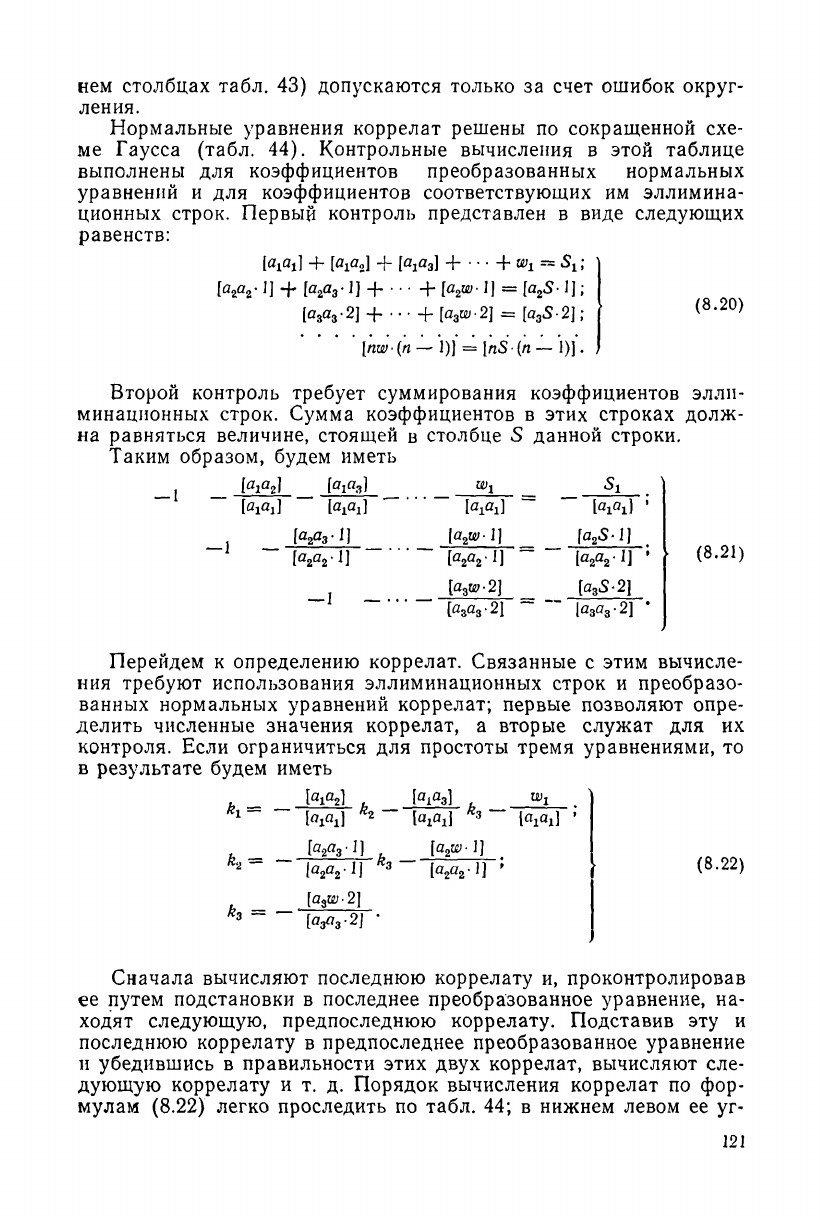
нем столбцах табл. 43) допускаются только за счет ошибок округ-

ления.

Нормальные уравнения коррелат решены по сокращенной схе-

ме Гаусса (табл. 44). Контрольные вычисления в этой таблице

выполнены для коэффициентов преобразованных нормальных

уравнений и для коэффициентов соответствующих им эллимина-

ционных строк. Первый контроль представлен в виде следующих

равенств:

[ял! 4- [ял! + l

a] Н Ь щ = 5

[а

< 1]

-f

[а

-J

Л + [ago-1] = [a

S-1];

[flaas-2]

H H

[а

В1-2] = [a

5-2] ;

\nw-(n—\)) = I/iS-(/i— 1)].

(8.20)

Второй контроль требует суммирования коэффициентов элли-

минационных строк. Сумма коэффициентов в этих строках долж-

на равняться величине, стоящей в столбце S данной строки.

Таким образом, будем иметь

•

[а

Л]

[а

. J]

1<W

(8.21)

Перейдем к определению коррелат. Связанные с этим вычисле-

ния требуют использования эллиминационных строк и преобразо-

ванных нормальных уравнений коррелат; первые позволяют опре-

делить численные значения коррелат, а вторые служат для их

контроля. Если ограничиться для простоты тремя уравнениями, то

в результате будем иметь

[QAl . [ДаАД] -

k, =

[а

(8.22)

Сначала вычисляют последнюю коррелату и, проконтролировав

ее путем подстановки в последнее преобразованное уравнение, на-

ходят следующую, предпоследнюю коррелату. Подставив эту и

последнюю коррелату в предпоследнее преобразованное уравнение

и убедившись в правильности этих двух коррелат, вычисляют сле-

дующую коррелату и т. д. Порядок вычисления коррелат по фор-

мулам (8.22) легко проследить по табл. 44; в нижнем левом ее уг-

121

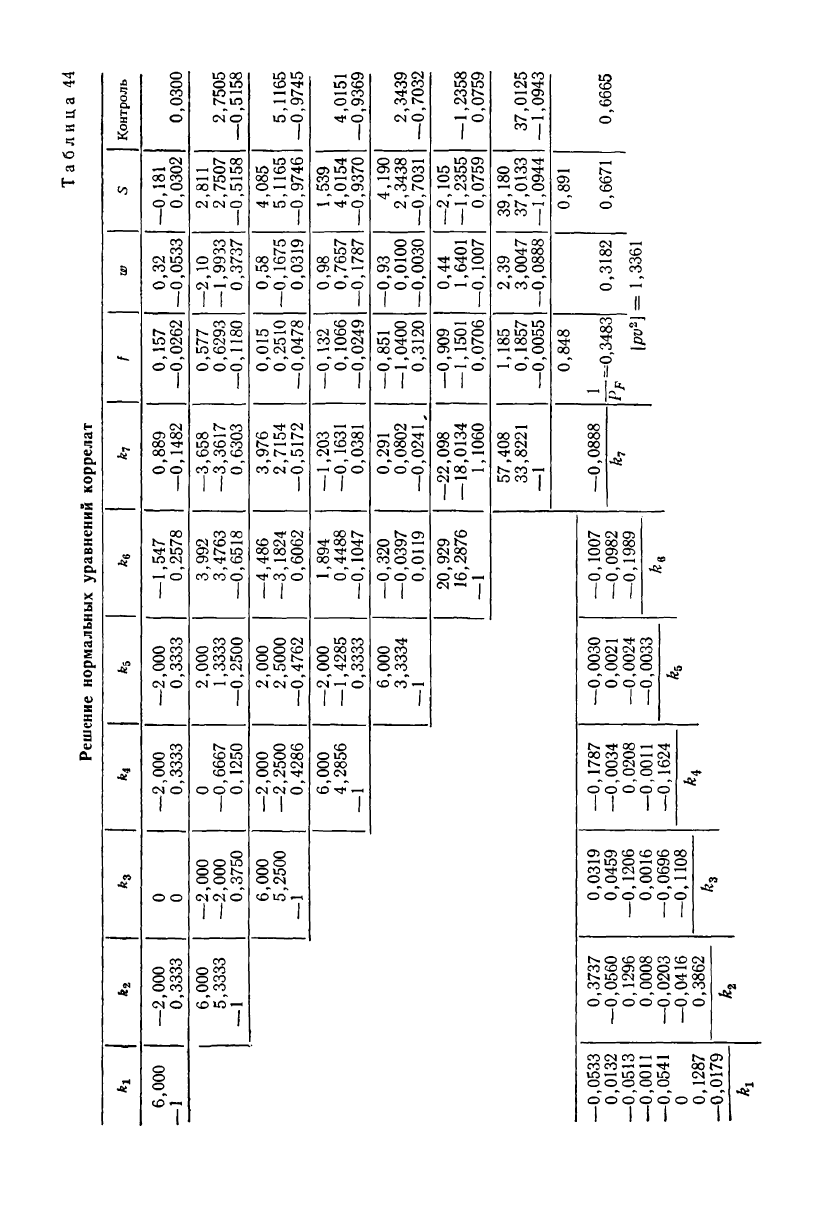
Таблица

Решение нормальных уравнений коррелат

*4 н

Контроль

6,000

—1

—2,000

0,3333

—2,000

0,3333

—2,000

0,3333

— 1,547

0,2578

0,889

—0,1482

0,157

—0,0262

0,32

—0,0533

—0,181

0,0302 0,0300

6,000

5,3333

— 1

—2,000

0,3750

—0,6667

0,1250

2,000

1,3333

—0,2500

3,992

3,4763

—0,6518

—3,658

—3,3617

0,6303

0,577

0,6293

—0,1180

—2,10

— 1,9933

0,3737

2,811

2,7507

—0,5158

2,7505

—0,5158

6,000

5,2500

—1

—2,000

—2,2500

0,4286

2,000

2,5000

—0,4762

—4,486

—3,1824

0,6062

3,976

2,7154

-0,5172

0,015

0,2510

—0,0478

0,58

—0,1675

0,0319

4,085

5,1165

—0,9746

5,1165

—0,9745

6,000

4,2856

— 1

—2,000

— 1,4285

0,3333

1,894

0,4488

—0,1047

— 1,203

—0,1631

0,0381

—0,132

0,1066

—0,0249

0,98

0,7657

—0,1787

1,539

4,0154

—0,9370

4,0151

—0,9369

6,000

3,3334

— 1

—0,320

—0,0397

0,0119

0,291

0,0802

—0,0241„

—0,851

—

1,0400

0,3120

—0,93

0,0100

—0,0030

4,190

2,3438

—0,7031

2,3439

—0,7032

20,929

16,2876

— 1

—22,098

— 18,0134

1,1060

—0,909

— 1,1501

0,0706

0,44

1,6401

—0,1007

—2,105

— 1,2355

0,0759

— 1,2358

0,0759

57,408

33,8221

—1

1,185

0,1857

—0,0055

2,39

3,0047

—0,0888

39,180

37,0133

—1,0944

37,0125

— 1,0943

—0,0888

0,848

ту-—0,3483

* F

1 pv

]

0,3182

1,3361

0,891

0,6671

0,6665

—0,0533

0,0132

—0,0513

—0,0011

—0,0541

0,1287

-0,0179

0,3737

—0,0560

0,1296

0,0008

—0,0203

—0,0416

0,3862

0,0319

0,0459

—0,1206

0,0016

—0,0696

—0,1108

—0,1787

—0,0034

0,0208

—0,0011

—0,1624

—0,0030

0,0021

—0,0024

—0,0033

—0,1007

—0,0982

—0,1989

—0,0888

0,848

ту-—0,3483

* F

1 pv

]

0,3182

1,3361

0,891

0,6671

0,6665

лу дана табличка слагаемых, участвующих в вычислении корре-

лат в соответствии с указанными формулами.

Вычислив коррелаты, находят поправки к измеренным направ-

лениям по формуле

« JT(яА + ЧК +

• • •

+ Mr), (8.23)

где щ— коэффициенты условных уравнений, ki — коррелаты. В на-

шей сети направления измерены равноточно, поэтому р,-= 1.

Поправки направлений, вычисленные по формуле (8.23), приве-

дены в табл. 42.

Контроль составления и решения системы нормальных уравне-

ний, соответствующих системе условных уравнений в табл. 42, вы-

полняется по формуле [pv

] = — \kw]. Если при составлении услов-

ных уравнений были допущены ошибки, то обнаружатся они толь-

ко при окончательном решении треугольников. Поэтому условные

уравнения надо составлять аккуратно, в две руки.

При уравнивании направлений на каждом пункте и в сети в

целом должно соблюдаться равенство [pv]= 0, т. е. сумма произ-

ведений поправок направлений на их веса должна быть равна

нулю.

В больших геодезических сетях, например в сети 2 класса, за-

полняющей полигон 1 класса, на точность определения поправок

из уравнивания к измеренным направлениям существенное влия-

ние оказывают ошибки округлений при вычислениях. Поэтому в

таких больших сетях необходимо нормальные уравнения состав-

лять и решать с существенно большим числом десятичных знаков,

чем это принято при уравнивании небольших сетей, где достаточ-

но ограничиться 4—5 десятичными знаками после запятой.

§ 39. Оценка точности уравненных элементов сети

Как отмечалось выше, для оценки точности того или иного эле-

мента уравненной сети необходимо составить соответствующую

ему функцию F и вычислить ее обратный вес 1//V Тогда средняя

квадратическая ошибка уравненного элемента определится по

формуле

^i]/ (8.24)

где

JJL

— средняя квадратическая ошибка единицы веса, опреде-

ляемая из уравнивания сети,

ILI

= /(W)77, (8.25)

v — поправки к измеренным с весами р величинам, г — число из-

быточных измерений, равное числу условных уравнений.

Обратный вес \/PF функции F уравненных элементов может

быть вычислен либо с использованием элементов обратной матри-

цы (8.17) весовых коэффициентов, получаемой путем обращения

123

матрицы N коэффициентов нормальных уравнений, либо в процес-

се решения системы нормальных уравнений по схеме Гаусса.

Рассмотрим последний прием решения данной задачи. В нашей

сети была составлена весовая функция f

(см. § 37) для оценки

точности длины наиболее удаленной стороны S34 и затем по фор-

муле

вычислен в табл. 44 при решении нормальных уравнений обрат-

ный вес этой стороны, который оказался равным 1/P

= 0,348.

Средняя квадратическая ошибка единицы веса равна

Среднюю квадратическую ошибку уравненного угла найдем из

выражения

уг

/2 =0,44 У2 = 0,62".

С учетом полученных значений

(я

= 0,44" и 1/P

= 0,348 найдем

среднюю квадратическую ошибку длины уравненной стороны s

Отметим, что полученная ошибка m

характеризует только

лишь точность передачи длины от исходной стороны s

к стороне

, причем без учета влияния ошибок исходных данных, которое

надо учесть дополнительно.

Вопрос учета влияния ошибок исходных данных на точность оп-

ределения уравненных элементов еще не отработан должным обра-

зом на практике, особенно в больших и сложных сетях многосту-

пенчатого построения. Поэтому в подавляющем числе случаев ог-

раничиваются вычислением средних квадратических ошибок

уравненных элементов по формуле (8.24), т. е. без учета влияния

ошибок исходных данных, что в ряде случаев, когда последние

ошибки сравнительно велики, приводит к некоторому завышению

показателей точности оцениваемых элементов, что надо иметь в

виду.

После исправления измеренных направлений поправками, по-

лученными из уравнивания сети, выполняют окончательное реше-

ние треугольников (табл. 45). Сумма уравненных углов в каждом

треугольнике должна быть равна 180°. Если поправки округлены

до сотых долей секунды, то сумма уравненных углов в некоторых

треугольниках может отличаться от 180° на 0,01". Обычно эту со-

тую долю секунды алгебраически прибавляют к углу, который

наиболее близок к прямому.

ггп_

1]2

2]2

3)2

K^I] [a

.2] [a

§ 40. Окончательные вычисления в триангуляции

124

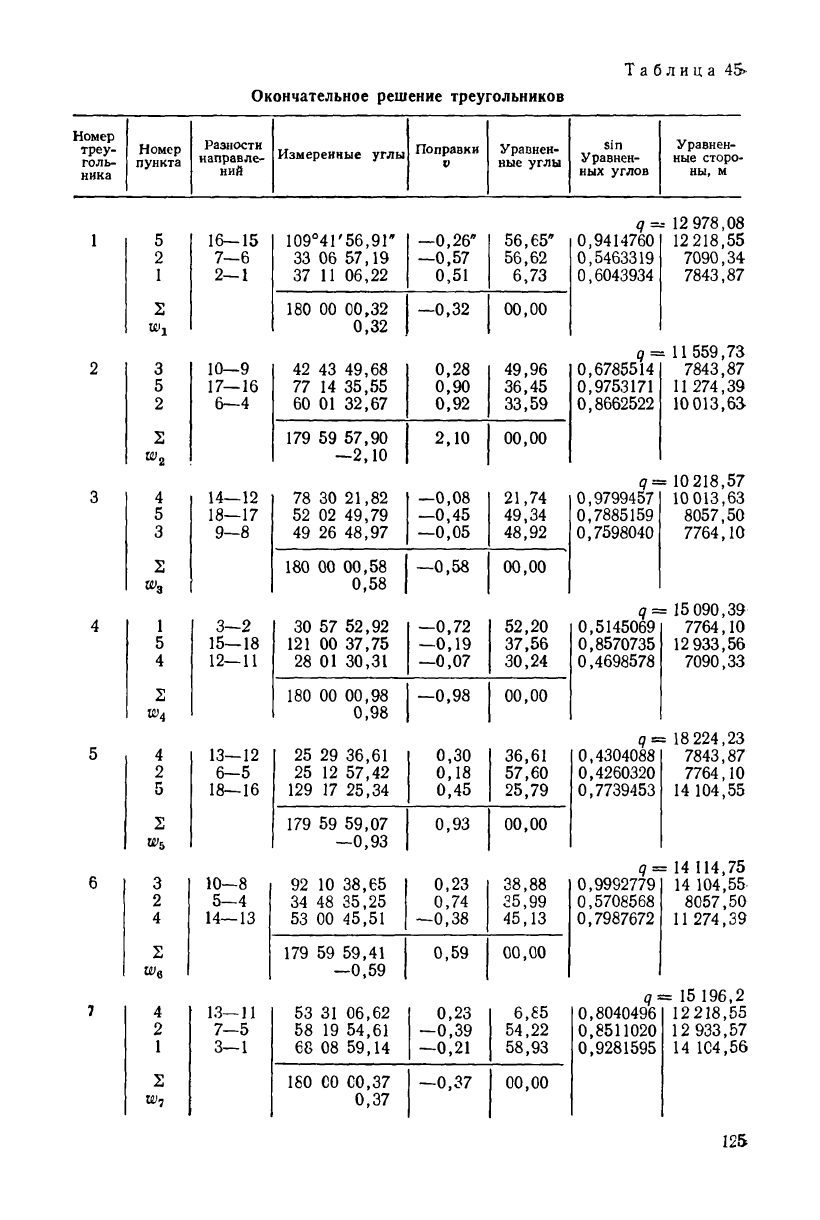
Таблица 78'

Окончательное решение треугольников

Номер

треу-

голь-

ника

Номер

пункта

Разности

направле-

ний

Измеренные углы

Поправки

Уравнен-

ные углы

sin

Уравнен-

ных углов

Уравнен-

ные сторо-

ны, м

1 5

16—15

7—6

2—1

109°4Г56,9Г

33 06 57,19

37 11 06,22

—0,26"

—0,57

0,51

56,65"

56,62

6,73

0,9414760

0,5463319

0,6043934

= 12 978,08

12218,55

7090,34

7843,87

КУ

180 00 00,32

0,32

—0,32

00,00

10—9

17—16

6—4

42 43 49,68

77 14 35,55

60 01 32,67

0,28

0,90

0,92

49,96

36,45

33,59

0,6785514

0,9753171

0,8662522

, 11 559,73

7843,87

11 274,39

10 013,6а

179 59 57,90

—2,10

2,10

00,00

3 4

14—12

18—17

9-8

78 30 21,82

52 02 49,79

49 26 48,97

—0,08

—0,45

—0,05

21,74

49,34

48,92

0,9799457

0,7885159

0,7598040

= 10218,57

10013,63

8057,50

7764,10

^з I

180 00 00,58 I

0,58 1

—0,58

00,00

3—2

15—18

12—11

30 57 52,92

121 00 37,75

28 01 30,31

—0,72

—0,19

—0,07

52,20

37,56

30,24

0,5145069

0,8570735

0,4698578

= 15 090,39

7764,10

12 933,56

7090,33

180 00 00,98

0,98 |

—0,98

| 00,00

13—12

6-5

18—16

25 29 36,61

25 12 57,42

129 17 25,34

0,30

0,18

0,45

36,61

57,60

25,79

0,4304088

0,4260320

0,7739453

= 18 224,23

7843,87

7764,10

14 104,55

179 59 59,07

—0,93

0,93 00,00

10—8

5-4

14—13

92 10 38,65 I

34 48 35,25

53 00 45,51 |

0,23

0,74

—0,38

38,88

25,99

45,13

0,9992779

0,5708568

0,7987672

= 14 114,75

14 104,55

8057,50

11 274,39

179 59 59,41

—0,59

0,59

00,00

13—11

7-5

3—1

53 31 06,62

58 19 54,61

68 08 59,14

0,23

—0,39

—0,21

6,85

54,22

58,93

0,8040496

0,8511020

0,9281595

= 15 196,2

12218,55

12 933,57

14 1С4,56

W 7

180 СО СО,37

0,37

—0,37

00,00

-125

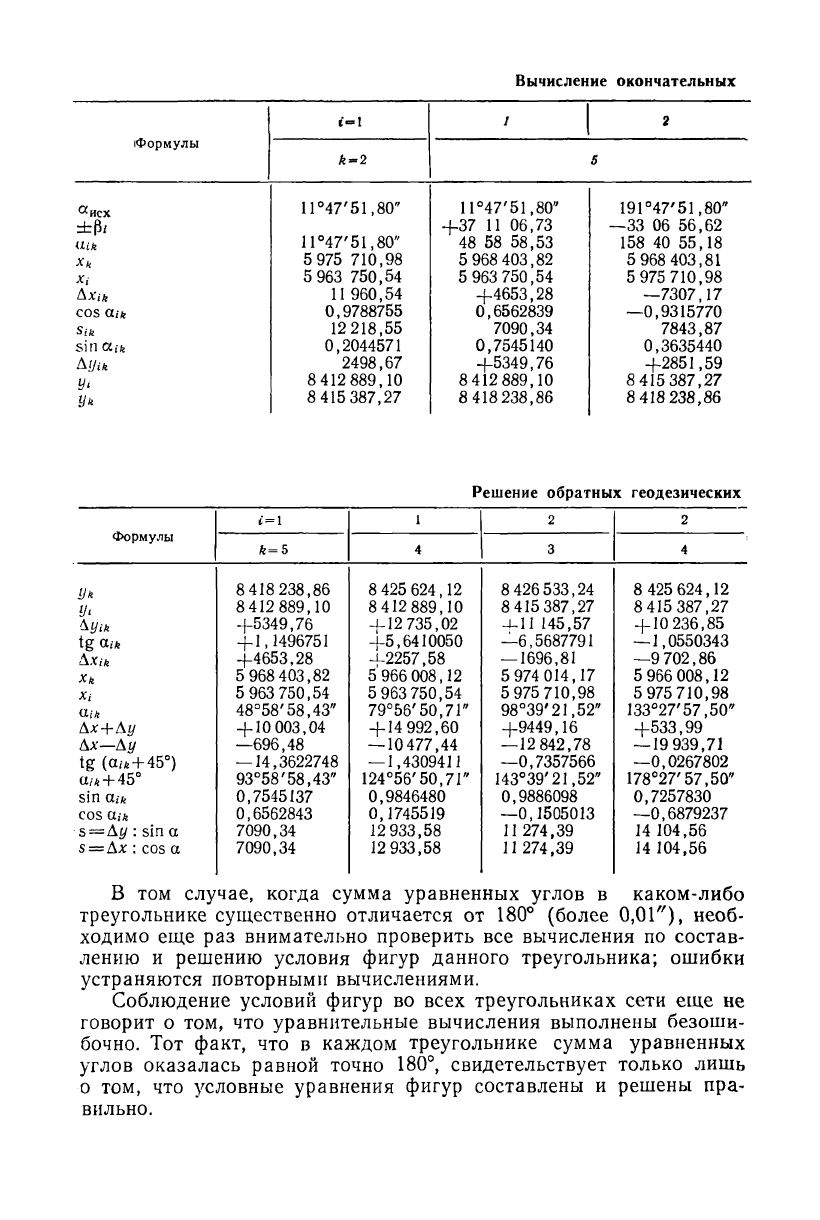
Вычисление окончательных

Формулы

i-l

Формулы

k = 2

®исх

11°47'51,80"

11°47'51,80" 191°47'51,80"

±р I

+37 11 06,73

—33 06 56,62

ть

11°47'51,80"

48 58 58,53

158 40 55,18

5 975 710,98

5 968 403,82

5 968 403,81

5 963 750,54

5 963 750,54 5 975 710,98

A Xik

11 960,54

+4653,28 —7307,17

COS Сiik

0,9788755

0,6562839

—0,9315770

Sik

12218,55

7090,34

7843,87

sin оiik

0,2044571

0,7545140

0,3635440

Al/ik

2498,67

+5349,76

+2851,59

i/i

8 412 889,10

8 415 387,27

Ilk

8 415 387,27

8 418 238,86

Решение обратных геодезических

Формулы

i*= 1

2 2

Формулы

k=b

Уь

8 418 238,86 8 425 624,12 8 426 533,24

8 425 624,12

8412 889,10 8412 889,10

8 415 387,27

byik

+5349,76

735,02

-4-11 145,57

236,85

tg aik

+ 1,1496751

+5,6410050

—6,5687791

— 1,0550343

'\Xi

+4653,28 +2257,58

— 1696,81

—9 702,86

5 968 403,82

5 966 008,12

5 974 014,17

5 966 008,12

5 963 750,54

5 975 710,98

(iik

48°58'58,43"

79°56' 50,71"

98°39'21,52" 133°27'57,50"

Ax+Ay

003,04

992,60

+9449,16

+533,99

Ax—Ay —696,48

—10477,44

—12 842,78

—19 939,71

tg (a/* + 45°)

— 14,3622748

—1,4309411

—0,7357566 —0,0267802

а/л+ 45°

93°58'58,43"

124°56'50,71"

143°39

21,52"

178°27' 57,50"

sin aik

0,7545137

0,9846480 0,9886098

0,7257830

cos a ik

0,6562843 0,1745519 —0,1505013

—0,6879237

s = Aу

sin a

7090,34

12 933,58

11 274,39 14 104,56

s=Ax : cos a

7090,34 12 933,58 11 274,39

14 104,56

В том случае, когда сумма уравненных углов в каком-либо

треугольнике существенно отличается от 180° (более 0,01"), необ-

ходимо еще раз внимательно проверить все вычисления по состав-

лению и решению условия фигур данного треугольника; ошибки

устраняются повторными вычислениями.

Соблюдение условий фигур во всех треугольниках сети еще не

говорит о том, что уравнительные вычисления выполнены безоши-

бочно. Тот факт, что в каждом треугольнике сумма уравненных

углов оказалась равной точно 180°, свидетельствует только лишь

о том, что условные уравнения фигур составлены и решены пра-

вильно.

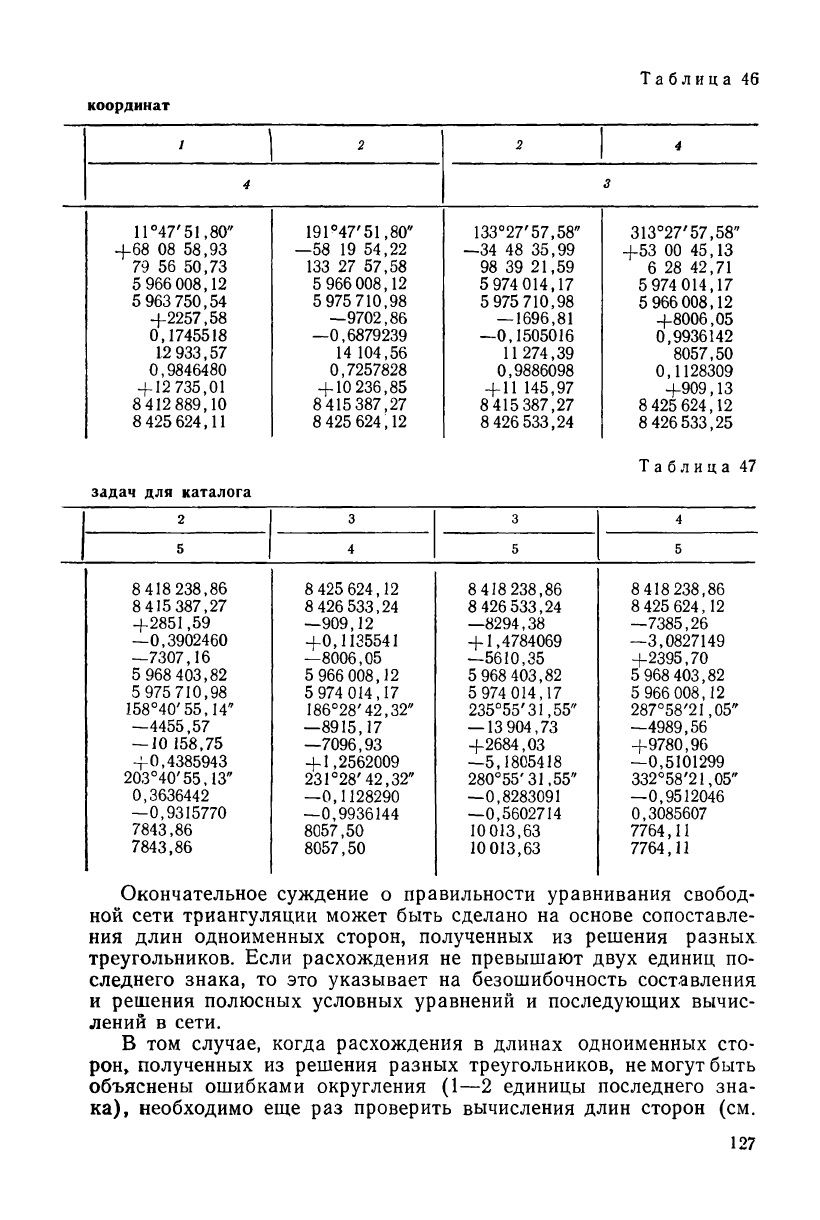
Таблица 78'

координат

11°47'51,80" 191°47'51,80"

133°27'57,58" 313°27

57,58"

+68 08 58,93

—58 19 54,22 —34 48 35,99

+53 00 45,13

79 56 50,73

133 27 57,58

98 39 21,59

6 28 42,71

5 966 008,12 5 966 008,12

5 974 014,17 5 974 014,17

5 963 750,54 5 975 710,98

5 975 710,98

5 966 008,12

+2257,58

—9702,86

— 1696,81

+8006,05

0,1745518

—0,6879239

—0,1505016 0,9936142

12 933,57 14 104,56

11 274,39

8057,50

0,9846480

0,7257828

0,9886098

0,1128309

+ 12 735,01

+ 10 236,85

145,97

+909,13

8 412 889,10 8 415 387,27

8 415 387,27

8 425 624,12

8 425 624,11

8 425 624,12

8 426 533,24

8 426533,25

Таблица 47

задач для каталога

8 418 238,86

8 415 387,27

+2851,59

—0,3902460

—7307,16

5 968 403,82

5 975 710,98

158°40' 55,14"

—4455,57

— 10 158,75

+0,4385943

203°40'55,13"

0,3636442

—0,9315770

7843,86

8 425 624,12

8 426 533,24

—909,12

+0,1135541

—8006,05

5 966 008,12

5 974 014,17

186°28'42,32"

—8915,17

—7096,93

+ 1,2562009

231°28' 42,32"

—0,1128290

—0,9936144

8057,50

8 418 238,86

8 426 533,24

—8294,38

+ 1,4784069

—5610,35

5 968 403,82

5 974 014,17

235°55'31,55"

— 13 904,73

+2684,03

—5,1805418

280°55'31,55"

—0,8283091

—0,5602714

10013,63

10 013,63

8418238,86

8 425 624,12

—7385,26

—3,0827149

+2395,70

5 968 403,82

5 966 008,12

287°58'21,05"

—4989,56

+9780,96

—0,5101299

332°58'21,05"

—0,9512046

0,3085607

7764,11

Окончательное суждение о правильности уравнивания свобод-

ной сети триангуляции может быть сделано на основе сопоставле-

ния длин одноименных сторон, полученных из решения разных

треугольников. Если расхождения не превышают двух единиц по-

следнего знака, то это указывает на безошибочность составления

и решения полюсных условных уравнений и последующих вычис-

лений в сети.

В том случае, когда расхождения в длинах одноименных сто-

рон, полученных из решения разных треугольников, не могут быть

объяснены ошибками округления (1—2 единицы последнего зна-

ка), необходимо еще раз проверить вычисления длин сторон (см.

-127

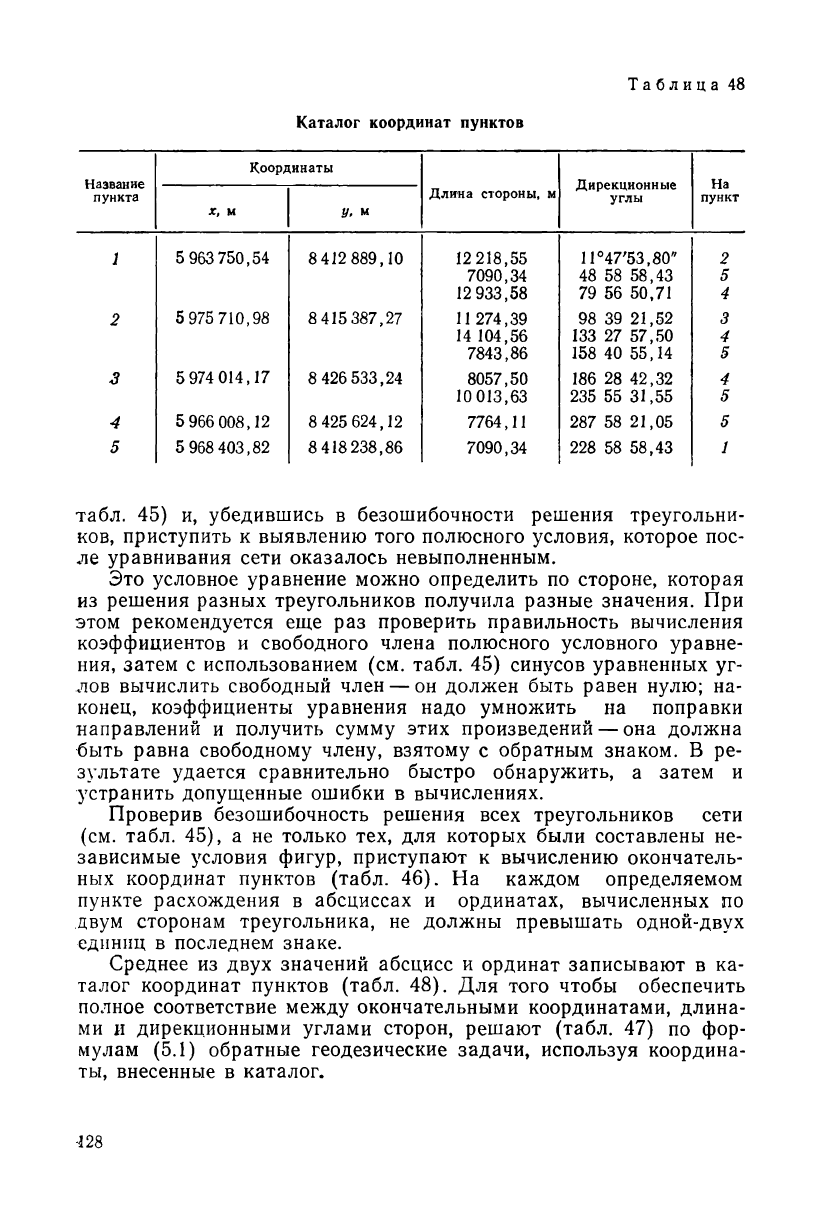
Таблица

78'

Каталог координат пунктов

Название

пункта

Координаты

Дирекционные

углы

На

пункт

Название

пункта

у. м

Длина стороны, м

Дирекционные

углы

На

пункт

5 963 750,54 8 412 889,10 12218,55

7090,34

12 933,58

11°47'53,80"

48 58 58,43

79 56 50,71

5 975 710,98

8 415 387,27

11 274,39

14 104,56

7843,86

98 39 21,52

133 27 57,50

158 40 55,14

5 974 014,17

8 426 533,24

8057,50

10013,63

186 28 42,32

235 55 31,55

5 966 008,12

8 425 624,12

7764,11

287 58 21,05

5 968 403,82 8 418 238,86

7090,34 228 58 58,43

табл. 45) и, убедившись в безошибочности решения треугольни-

ков, приступить к выявлению того полюсного условия, которое пос-

ле уравнивания сети оказалось невыполненным.

Это условное уравнение можно определить по стороне, которая

из решения разных треугольников получила разные значения. При

этом рекомендуется еще раз проверить правильность вычисления

коэффициентов и свободного члена полюсного условного уравне-

ния, затем с использованием (см. табл. 45) синусов уравненных уг-

лов вычислить свободный член — он должен быть равен нулю; на-

конец, коэффициенты уравнения надо умножить на поправки

направлений и получить сумму этих произведений — она должна

быть равна свободному члену, взятому с обратным знаком. В ре-

зультате удается сравнительно быстро обнаружить, а затем и

устранить допущенные ошибки в вычислениях.

Проверив безошибочность решения всех треугольников сети

(см. табл. 45), а не только тех, для которых были составлены не-

зависимые условия фигур, приступают к вычислению окончатель-

ных координат пунктов (табл. 46). На каждом определяемом

пункте расхождения в абсциссах и ординатах, вычисленных по

двум сторонам треугольника, не должны превышать одной-двух

единиц в последнем знаке.

Среднее из двух значений абсцисс и ординат записывают в ка-

талог координат пунктов (табл. 48). Для того чтобы обеспечить

полное соответствие между окончательными координатами, длина-

ми и дирекционными углами сторон, решают (табл. 47) по фор-

мулам (5.1) обратные геодезические задачи, используя координа-

ты, внесенные в каталог.

-128