Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

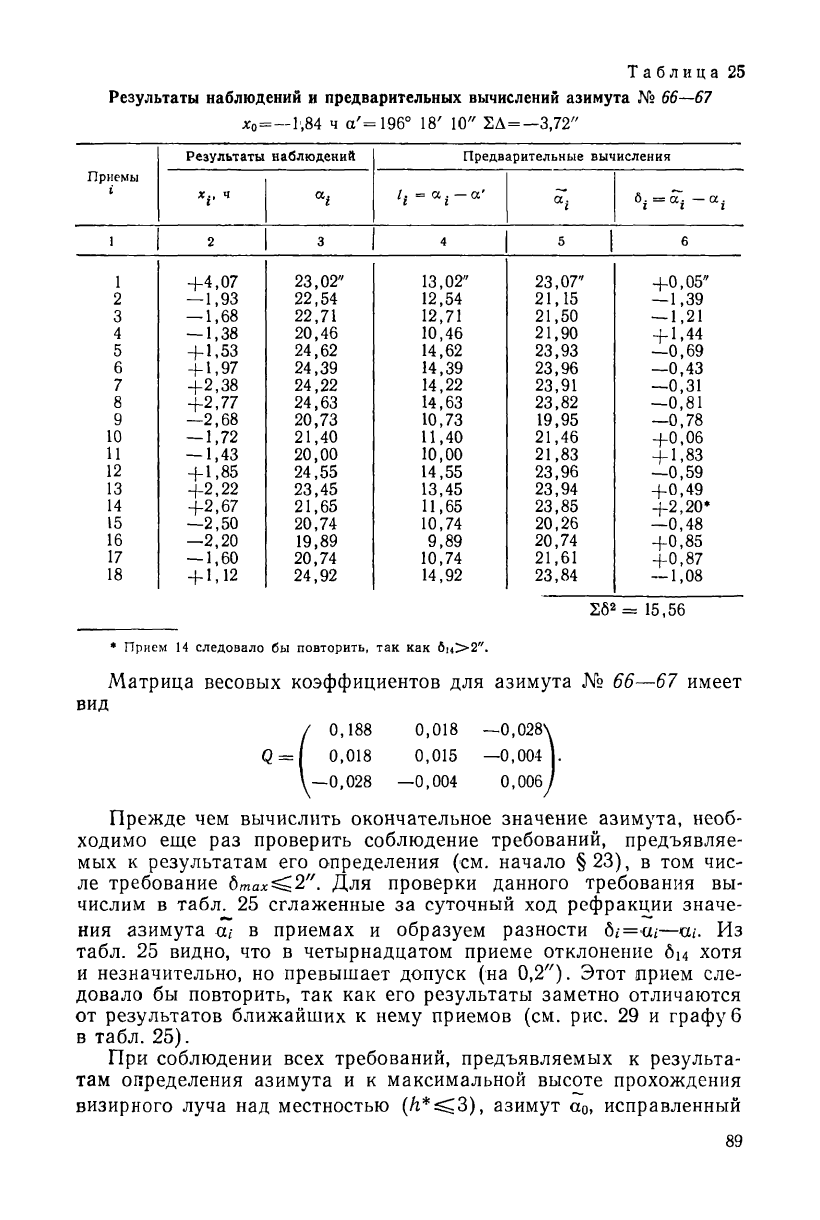
Таблица 25

Результаты наблюдений и предварительных вычислений азимута № 66—67

ЛГ

=—1,84 ч а' =196° 18

10" 2Д= — 3,72"

Результаты наблюдений

Предварительные вычисления

Приемы

X., ч

/. = а.-а'

«1

i = «i

- 1

1 +4,07 23,02"

13,02"

23,07"

+0,05"

2 — 1,93

22,54 12,54

21,15

— 1,39

—

1,68

22,71

12,71

21,50

—1,21

—

1,38

20,46 10,46

21,90

+ 1,44

+ 1,53

24,62

14,62

23,93

—0,69

+ 1,97

24,39 14,39

23,96

—0,43

7 +2,38

24,22

14,22

23,91

—0,31

+2,77

24,63

14,63

23,82

—0,81

9 —2,68

20,73 10,73 19,95

—0,78

— 1,72

21,40

11,40 21,46

+0,06

—

1,43

20,00

10,00 21,83

+ 1,83

+ 1,85 24,55 14,55

23,96

—0,59

13 +2,22

23,45 13,45

23,94

+0,49

+2,67

21,65

11,65

23,85 +2,20*

—2,50 20,74

10,74

20,26

—0,48

—2,20

19,89 9,89

20,74

+0,85

—

1,60 20,74 10,74

21,61

+0,87

+ 1,12

24,92

14,92

23,84

— 1,08

= 15,56

* Прием 14 следовало бы повторить, так как бц>2".

Матрица весовых коэффициентов для азимута № 66—67 имеет

вид

(0,188 0,018 —0,028\

0,018 0,015 —0,004

—0,028 —0,004 0,006у

Прежде чем вычислить окончательное значение азимута, необ-

ходимо еще раз проверить соблюдение требований, предъявляе-

мых к результатам его определения (см. начало §23), в том чис-

ле требование 6тах^2". Для проверки данного требования вы-

числим в табл. 25 сглаженные за суточный ход рефракции значе-

ния азимута щ в приемах и образуем разности 6, = ш—кн. Из

табл. 25 видно, что в четырнадцатом приеме отклонение 6м хотя

и незначительно, но превышает допуск (на 0,2"). Этот прием сле-

довало бы повторить, так как его результаты заметно отличаются

от результатов ближайших к нему приемов (см. рис. 29 и графу б

в табл. 25).

При соблюдении всех требований, предъявляемых к результа-

там определения азимута и к максимальной высоте прохождения

визирного луча над местностью (/г*^3), азимут а

, исправленный

за влияние боковой рефракции, вычисляют по формуле (6.25).

Для рассматриваемого здесь азимута № 66—67 по формуле (6.25)

найдем исправленное за рефракцию значение:

= а' + а

+ а

= 196°18'10" + 11,29" = 196°18'21,28".

Прибавив к этому результату сумму всех поправок в азимут

2Д, приведенную в табл. 25, найдем исправленное за рефракцию

окончательное значение азимута

= а

+ 2Д, а

= 196°18'21,28" — 3,72" «

196°

18'17,56". (6.46)

Вычислим среднюю квадратическую ошибку единицы веса

т/ 2б

-Ж

Г 15,16

Обратный вес азимута, исправленного за рефракцию, вычис-

лим по формуле

(6.47)

ССо

или, что все равно, по формуле

-pZT = Qn + 2Q

+ (Q

+ 2Q

) V + 2Q

3 + Q

V, (6.48)

Cto

где f*=(lx

)—транспонированный по отношению к / вектор-

строка коэффициентов при определяемых величинах а

, а\> а

ап-

проксимирующей функции (6.27); Q

— элементы матрицы Q ве-

совых коэффициентов (6.45);

Хо

— средний для азимута момент

изотермии воздуха, когда влияние боковой рефракции равно или

почти равно нулю.

Подставив в формулу (6.48) значения величин Q,j и хо, найдем

обратный вес азимута

-pi- =0,188 + 2 х 0,018(—1,84)+ (0,015- 2 х 0,028) (—1,84)

+ 2(—0,004) (— 1,84)

+ 0,006(— 1,84)

= 0,102.

Величину средней квадратической ошибки окончательного зна-

чения азимута ао, исправленного за влияние боковой рефракции,

вычислим по формуле

= \i 1 / = 1,02 /0ТТ02 = 0,33".

У «о

§ 26. Уравнивание на станции направлений, измеренных

в двух группах с одинаковыми весами

На пунктах с большим числом направлений последние измеря-

ют нередко в двух группах, имеющих не менее двух общих на-

правлений. В каждой группе направления измеряют с одним и

тем же весом. Если начальные направления в группах разные, то

измеренные в этих группах направления приводят к общему на-

чальному направлению и затем приступают к их уравниванию.

Порядок уравнивания направлений, измеренных в двух груп-

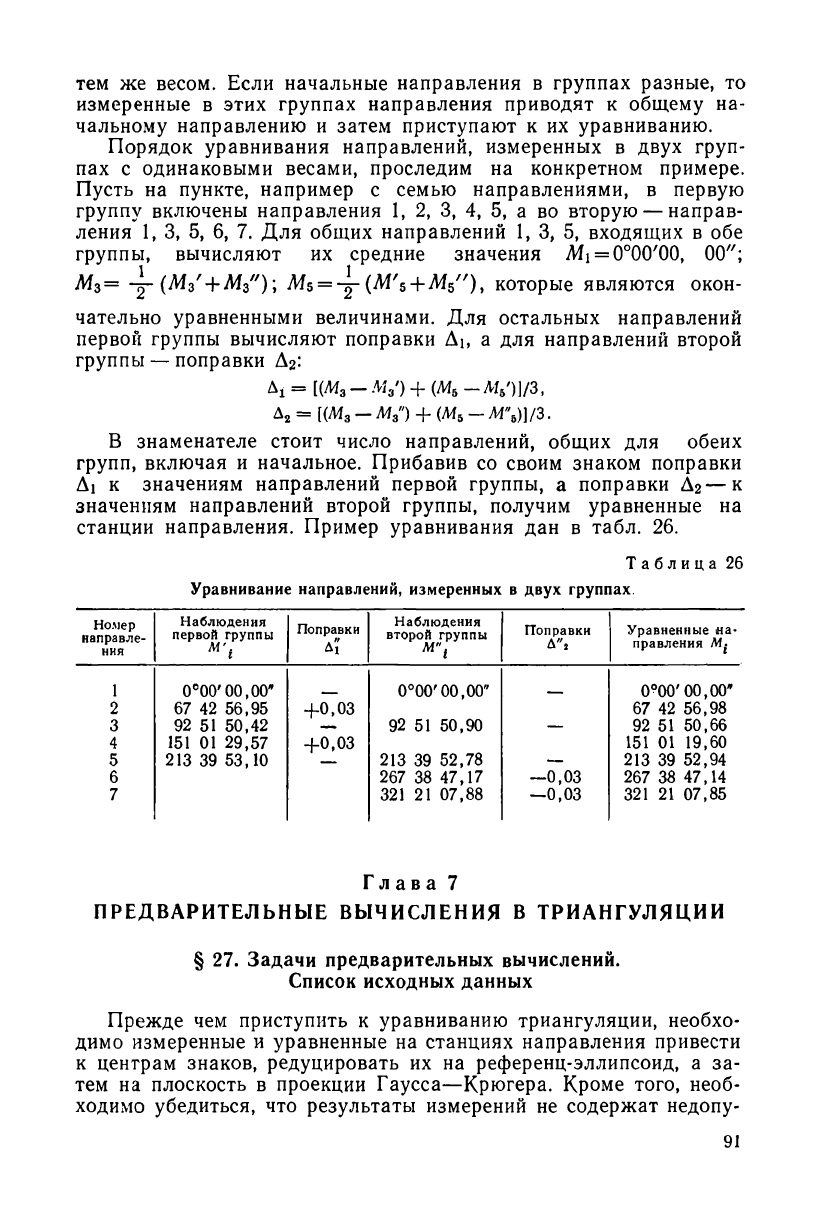
пах с одинаковыми весами, проследим на конкретном примере.

Пусть на пункте, например с семью направлениями, в первую

группу включены направления 1, 2, 3, 4, 5, а во вторую — направ-

ления 1, 3, 5, 6, 7. Для общих направлений 1, 3, 5, входящих в обе

группы, вычисляют их средние значения Mi = 0°00'00, 00";

= (Мз' + Мз");

Af5

= -?r(M'5+М$")

которые являются окон-

чательно уравненными величинами. Для остальных направлений

первой группы вычисляют поправки Дь а для направлений второй

группы — поправки Дг:

Ai =

1(М

- AV) + (М

—

AV)]/3,

= №

- М

") + (М

- УИ"

)]/3.

В знаменателе стоит число направлений, общих для обеих

групп, включая и начальное. Прибавив со своим знаком поправки

А\ к значениям направлений первой группы, а поправки Д

—к

значениям направлений второй группы, получим уравненные на

станции направления. Пример уравнивания дан в табл. 26.

Таблица 26

Уравнивание направлений, измеренных в двух группах.

Но.мер

направле-

ния

Наблюдения

первой группы

М>.

Поправки

л"

Наблюдения

второй группы

Поправки

Д"2

Уравненные на-

правления м.

0°00' 00,00"

67 42 56,95

92 51 50,42

151 01 29,57

213 39 53,10

+0,03

0°00'00,00"

92 51 50,90

213 39 52,78

267 38 47,17

321 21 07,88

-0,03

0°00'00,00"

67 42 56,98

92 51 50,66

151 01 19,60

213 39 52,94

267 38 47,14

321 21 07,85

Глава 7

ПРЕДВАРИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В ТРИАНГУЛЯЦИИ

§ 27. Задачи предварительных вычислений.

Список исходных данных

Прежде чем приступить к уравниванию триангуляции, необхо-

димо измеренные и уравненные на станциях направления привести

к центрам знаков, редуцировать их на референц-эллипсоид, а за-

тем на плоскость в проекции Гаусса—Крюгера. Кроме того, необ-

ходимо убедиться, что результаты измерений не содержат недопу-

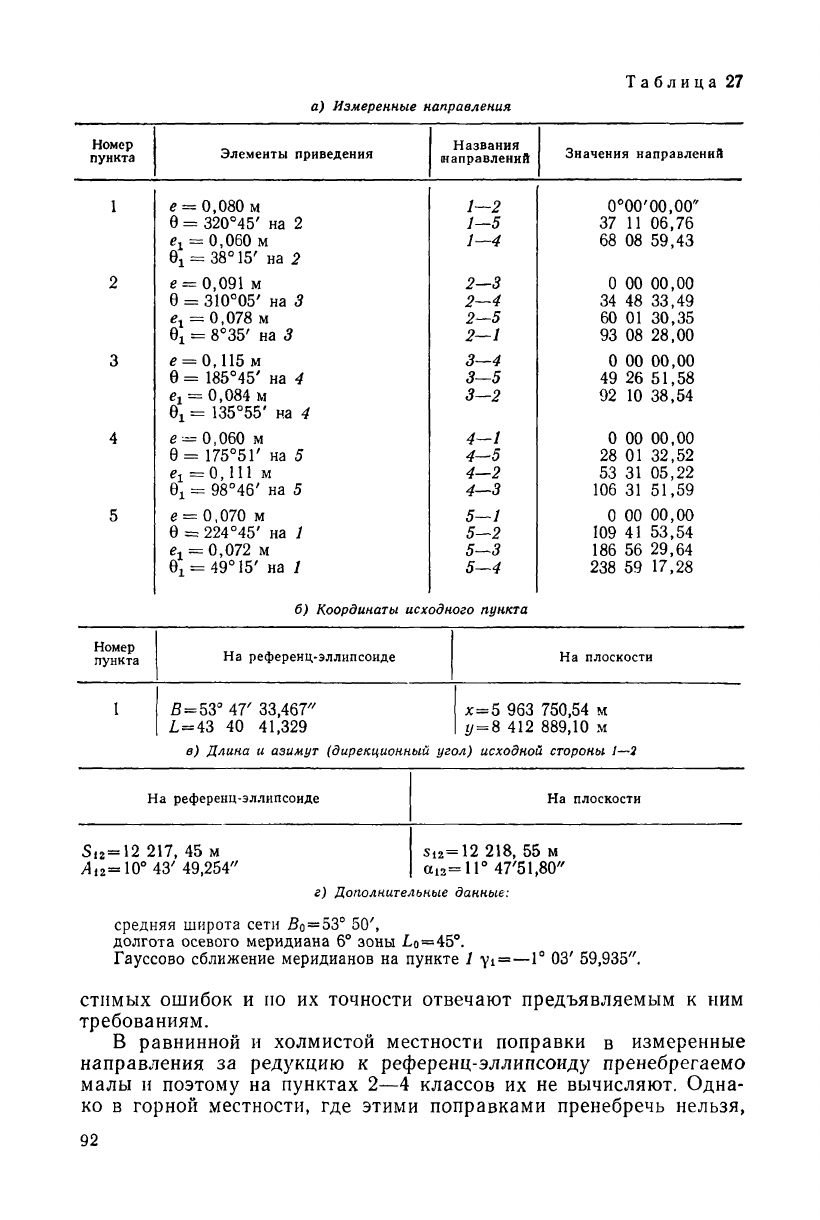
а) Измеренные направления

Таблица 27

Элементы приведения

Названия

(направлений

Значения направлений

е = 0,080 м

0 = 320°45' на 2

= 0,060 м

9j =

38° 15'

на 2

е = 0,091 м

9 = 310°05' на 3

= 0,078 м

= 8°35' на 3

£ = 0,115 м

0 = 185°45' на 4

= 0,084 м

= 135°55' на 4

0,060 м

0= 175°51' на 5

^ = 0,111 м

= 98°46' на 5

е = 0,070 м

0 = 224°45' на 1

0,072 м

49° 15'

на 1

1—2

1—5

1—4

2—3

2-4

2—5

2—1

3—4

3—5

3-2

4-1

4-5

4—2

4—3

5—1

5-2

5-3

5-4

б) Координаты исходного пункта

0°00'00,00"

37 11 06,76

68 08 59,43

00 00,00

34 48 33,49

60 01 30,35

93 08 28,00

О 00 00,00

49 26 51,58

92 10 38,54

О 00 00,00

28 01 32,52

53 31 05,22

106 31 51,59

О 00 00,00

109 41 53,54

186 56 29,64

238 59 17,28

Номер

пункта

На референц-эллипсоиде

На плоскости

53°

47' 33,467"

40 41,329

х=5 963 750,54 м

у = 8

412 889,10 м

в) Длина и азимут (дирекционный угол) исходной стороны. 1—2

На референц-эллипсоиде На плоскости

=12 217, 45 м

Si2= 12 218, 55 м

>1,2=10° 43' 49,254"

=11° 47'51,80"

г) Дополнительные данные:

средняя широта сети

Во

53°

50',

долгота осевого меридиана 6° зоны Lo=45°.

Гауссово сближение меридианов на пункте 1 yi =—Г 03' 59,935".

стимых ошибок и но их точности отвечают предъявляемым к ним

требованиям.

В равнинной и холмистой местности поправки в измеренные

направления за редукцию к референц-эллипсоиду пренебрегаемо

малы и поэтому на пунктах 2—4 классов их не вычисляют. Одна-

ко в горной местности, где этими поправками пренебречь нельзя,

(з)

их необходимо вычислять и учиты-

вать. Пример вычисления таких по-

правок дан в § 99.

Исходные стороны, измеренные

между центрами знаков и приве-

денные к поверхности референц-эл-

липсоида, необходимо также реду-

цировать на плоскость. От геоде-

зических азимутов исходных сто-

рон, заданных на поверхности ре-

ференц-эллипсоида, надо перейти к

дирекционным углам на плоскости.

Все виды предварительных вы-

числений проследим в порядке их

выполнения на небольшой свобод-

ной сети триангуляции 2 класса,

изображенной на рис. 31.

Результаты измерения направлений, численные значения эле-

ментов центрировок и редукций (е, б, е

6i), а также исходные

данные, которые потребуются для вычисления сторон и координат

сети, приведены в табл. 27.

РИС. 31

§ 28. Предварительное решение треугольников

и вычисление сферических избытков

Для того чтобы вычислить поправки в измеренные направле-

ния за центрировку теодолита и редукции визирных целей, необ-

ходимо найти сначала длины сторон треугольников. Попутно с ре-

шением треугольников вычисляют их сферические избытки.

Последовательность вычисления сторон треугольников и сфери-

ческих избытков можно проследить по табл. 28. При решении тре-

угольников целесообразно придерживаться следующих рекоменда-

ций:

выделить на схеме сети цепочку последовательного решения

треугольников и пронумеровать их по порядку. Треугольники, не

попадающие в эту цепочку, нумеруются и решаются последними;

в каждом треугольнике на первом месте выписывается номер

вершины того угла, который лежит против исходной стороны, а на

последнем — против стороны, которая служит исходной при реше-

нии следующего треугольника;

углы выписывают, округляя их до 10", причем так, чтобы сум-

ма углов в треугольнике была равна точно 180°;

противолежащие углы и стороны треугольника записывают по-

строчно.

В треугольнике с измеренными углами Л, В, С длины противо-

лежащих сторон вычисляют по теореме синусов углов:

а Ь с

sin

5=5

sin В ~ sin С

эа

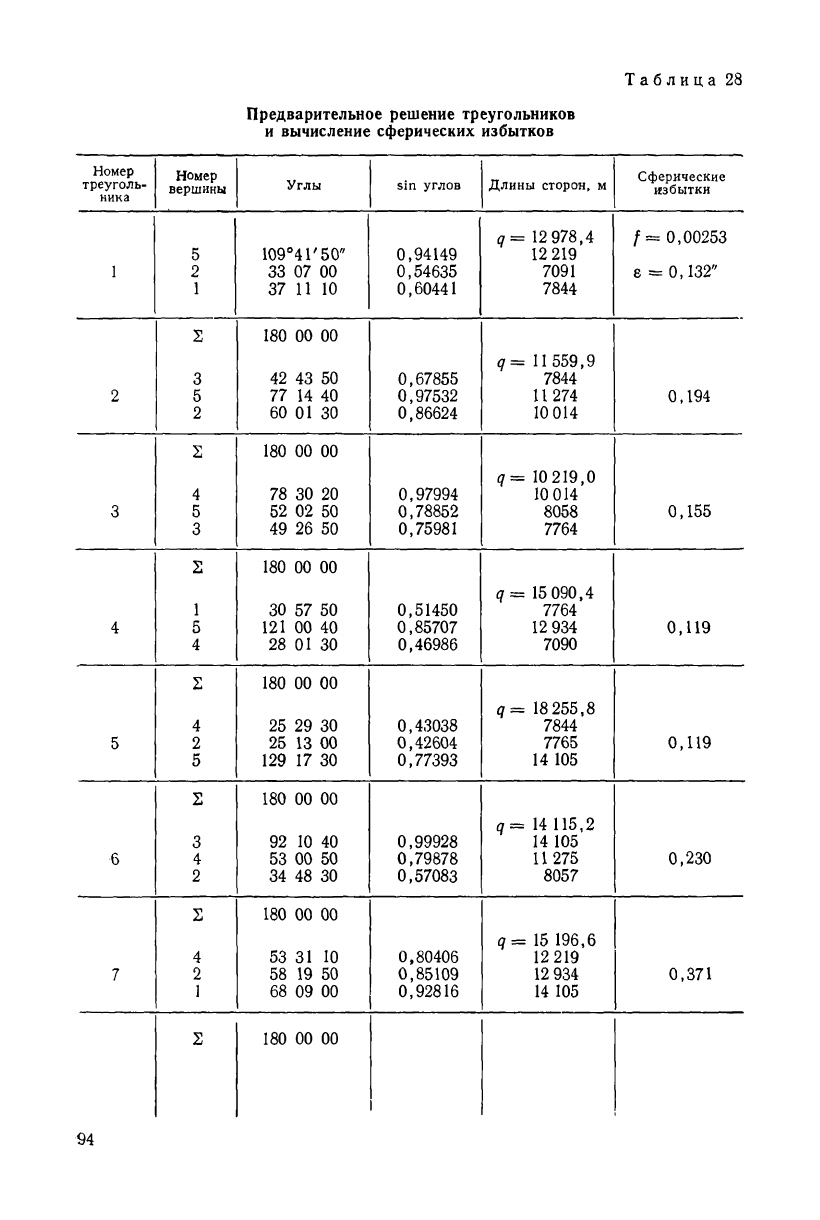
Таблица 28

Предварительное решение треугольников

и вычисление сферических избытков

Номер

треуголь-

ника

Номер

вершины

Углы sin углов

Длины сторон, м

Сферические

избытки

109°41'50"

33 07 00

37 И 10

0,94149

0,54635

0,60441

а =

978,4

219

7091

7844

/ = 0,00253

е = 0,132"

180 00 00

42 43 50

77 14 40

60 01 30

0,67855

0,97532

0,86624

q =

559,9

7844

11274

014

0,194

180 00 00

78 30 20

52 02 50

49 26 50

0,97994

0,78852

0,75981

<7= 10219,0

014

8058

7764

0,155

180 00 00

30 57 50

121 00 40

28 01 30

0,51450

0,85707

0,46986

q ~

090,4

7764

934

7090

0,119

180 00 00

25 29 30

25 13 00

129 17 30

0,43038

0,42604

0,77393

255,8

7844

7765

14 105

0,119

180 00 00

92 10 40

53 00 50

34 48 30

0,99928

0,79878

0,57083

<7= 14 115,2

14 105

11275

8057

0,230

180 00 00

53 31 10

58 19 50

68 09 00

0,80406

0,85109

0,92816

= 15 196,6

219

934

14 105

0,371

2 180 00 00

откуда, приняв сторону а за исходную, находят длины других сто-

рон

b = qsinB, c — qsinC.

Вычисление сторон треугольников начинается от исходной сто-

роны триангуляции. Величина q записывается над вычисляемыми

сторонами треугольника. Длина каждой стороны находится путем

умножения величины q на синус противолежащего угла. Длины

сторон вычисляют до целого метра.

Для первого треугольника с вершинами /, 2, 5 получим

219

^ ет 0^4149 -12ЭТ8.4,

= q sin 2 = 12 978,4X0,54635 = 7091 м,

= qs\nl = 12978,4x0,60441 = 7844 м.

Сферический избыток треугольника со сторонами а, Ь, с вычис-

ляют по формуле

е = fab sin С, (7.1)

где стороны а,

выражают в километрах, а коэффициент f = Р* -

в котором р

=206 265, a R

— средний радиус кривизны поверх-

ности земного эллипсоида на широте сети, выраженный также в

километрах, выбирают из прил. 1. В триангуляции 3—4 классов

значение этого коэффициента для территории СССР принимается

одинаковым и равным

[

= 0,00253.

Сферические избытки треугольников вычисляют до 0,001" в

триангуляции 1—2 классов и до 0,01" в триангуляции 3—4 клас-

сов.

§ 29. Вычисление элементов приведения,

определенных аналитическим способом

На пунктах триангуляции элементы центрировок и редукций

обычно малы и определяются графическим способом. Однако в

практике геодезических работ встречаются случаи, когда линей-

ные элементы центрировок или

редукций слишком велики для

графических определений (более

0,2—0,3 м). В таких случаях они

определяются аналитическими

методами. На местности измеря-

ется базис

Ь\

= АВ, а также углы

на его концах: A

и А

, В

, где

i — точка стояния теодолита на

геодезическом знаке; с — центр

пункта (рис. 32). Угол у при точ-

РИС

- 32

ке i измеряется в целях контроля.

Для ориентирования линейного элемента

= ic относительно на-

чального направления на пункте измеряется угол р.

Для вычисления значений элементов приведения (е, 0) введем

местную систему координат с началом в точке А и осью ординат,

совмещенной с направлением базиса АВ (см. рис. 32). Линейный

e=ic и угловой 0=<aW элементы центрировки теодолита найдем

по формулам

в = (360° - щ

) + (90° + ВЦ + Р,

(7.2)

(7.3)

где

t gBi

'igAi + tgBr

-°\gA

+ \gB

Xi =y

tgAi; x

= y

tgA

;

Ус —Ух

igB

(7.4)

По таким же формулам вычисляют элементы редукции.

Для контроля элементы приведений определяют дважды из из-

мерений с двух базисов Ь\ и Ь

с совмещенными концами в на-

чальной точке, как показано на рис. 32. Чтобы не загромождать

чертеж, углы А и В при втором базисе не показаны.

Таблица 29

Вычисление элементов приведения

Формулы

1-й базкс 2-й базис Формулы

1-й базис 2-Й базис

41,18 м

47,09 м

Хс

43,151

43,458

Ас

86°29,V

88° 29,2' 41,396 41,718

Вс

48 14,3

43 24,5

Хс —

1,755 1,740

85 51,2 87 51,9

3,2032

3,1932

47°18,9'

42°29,7'

1,790 м

1,787 м

16,27989

37,85124

tga ic

—0,20000

—0,23391

t gB

1,11995

0,94593

348°41,4'

346°50,1'

tg^ + tg B

17,39984

38,79717 360°—

18,6'

13°09,9'

t gA

13,79312

26,82368

90° + Bi 137 18,9 132 29,7

tg B

tgAi + ig Bi

1,08426

0,91617

83 37,4

86 28,2

tg B

tgAi + ig Bi

14,87738

27,73985

232 14,9

232 07,8

Ус

2,651 1,148

Среднее из

Ух

3,001 1,555 двух опре-

ср

= 232°1Г

Ус — Уг

—0,351

—0,407

делений

ср

= 1,788 м

ср

= 232°1Г

В табл. 29 дан пример вычисления элементов центрировки е

и 0 по измерениям с двух базисов:

1-й базис

£>

= 41,18 м A

— 85°51,2'

= 86°29,2' Bi

—

47 18,9

—

48 14,3 у = 46 49,8

р = 83 37,4 2 = 175 59,9

2-й базис

= 47,09 м

= 88°29,2'

24,5

Р = 86 28,2

= 87°51,9'

29,7

38,4

2 = 180 00,0

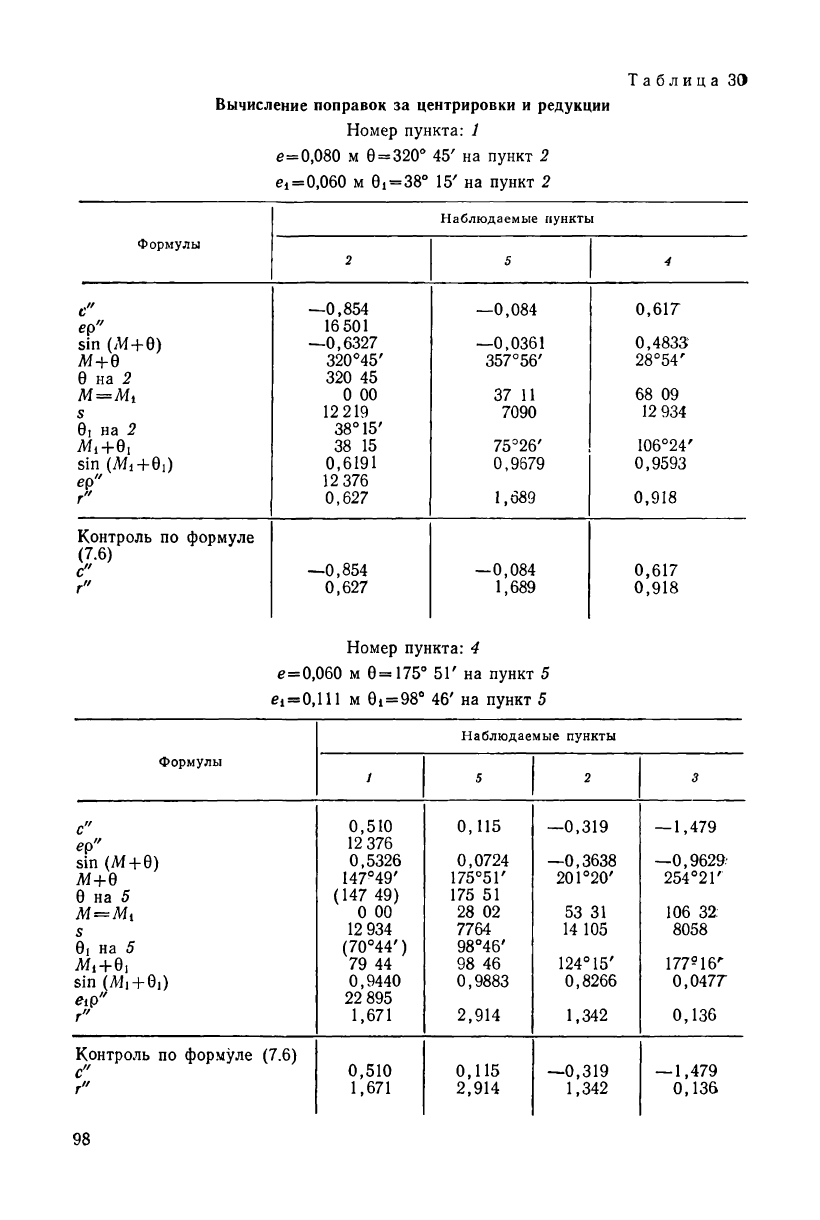
§ 30. Вычисление поправок за центрировку и редукцию

На каждом пункте триангуляции, на котором исполнены угло-

вые измерения, проекции точки I стояния теодолита, визирной це-

ли знака S и его центра С на горизонтальную плоскость не сов-

падают между собой (рис. 33). В связи с этим все измеренные в

точке I направления должны

быть приведены к центру знака

в точке С, т. е. исправлены по-

правками с" за центрировку тео-

долита. Эти поправки прибавля-

ются со своими знаками к изме-

ренным на данном пункте на-

правлениям /Л, IB и т. д.

Поправки г" за редукцию ви-

зирной цели S данного пункта

вводятся со своими знаками в об-

ратные направления, например

AS, BS (см. рис. 33), поскольку

визирование с точек Л, В, ... про-

изводится не на центр данного

знака в точке С, а на его визир-

ную цель в точке S.

Поправки за центрировку теодолита и редукцию визирной це-

ли вычисляют по формулам

РИС. 33

sin да+ 6) „

г =-

(7.5)

где е> 0 и ей 8i—элементы центрировки и редукции, М и М\ —

значения измеренных направлений, для которых вычисляются по-

правки, s — расстояние между пунктами.

Линейные элементы е и е\ определяют на центрировочных лис-

тах до целого миллиметра, а углы 0 и 0j — с графической точно-

стью порядка 15'.

Для контроля вычисления поправок с" и г" можно воспользо-

ваться таблицами величин (а) =—20,6265 sin

(Л1

+ 0), приведенны-

ми, например, в [13]. Если линейные элементы е я е\ выразить в

дециметрах, а расстояния 5 — в километрах, то

(0)

- = (7.6)

С •е;

Поправки за центрировку и редукцию в триангуляции 1—2

классов вычисляют до 0,001", а в триангуляции 3—4 классов до

7—2296

Таблица

Вычисление поправок

за

центрировки

редукции

Номер пункта:

е=0,080

320°

45' на

пункт

e?i=0,060

38°

15' на

пункт

Наблюдаемые пункты

Формулы

с"

—0,854

—0,084

0,617

ер"

16501

—0,084

sin (М+0)

—0,6327

—0,0361

0,4833

М+0

320°45'

357°56'

28°54'

0 на 2

320 45

M=M

0 00 37 И

68 09

12219

7090

934

0i на 2

38°15'

М1 + 0!

38 15

75°26

106°24'

sin

(Mi

+ 00

0,6191

0,9679

0,9593

ер"

376

г"

0,627

1,689 0,918

Контроль

по

формуле

(7.6)

с"

—0,854

—0,084

0,617

г"

0,627

1,689

0,918

Номер пункта:

е=0,060

0=175°

5Г на

пункт

0,111

01=98°

46' на

пункт

Наблюдаемые пункты

Формулы

с"

0,510

0,115

—0,319

— 1,479

ер"

376

— 1,479

sin (М + 0)

0,5326 0,0724

—0,3638

—0,9629

М+0

147°49'

175°5Г 201°20'

254°2Г

0 на 5

(147 49)

175 51

M==Mi

0 00

28 02

53 31

106 32:

934

7764

14 105

8058

0i на 5

(70°44')

98°46'

+ 0,

79 44

98 46

124°15'

177

sin

(М1

+ О1)

0,9440

0,9883

0,8266 0,0477

eip"

22 895

г"

1,671

2,914

1,342 0,136

Контроль

по

формуле

(7.6)

0,510

0,115

(Г

0,510

0,115

—0,319

— 1,479

г"

1,671

2,914

1,342 0,136