Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

®,Q1", а затем их сумму для каждого направления, приведенного

к начальному, округляют до 0,01 и 0,1" соответственно.

Порядок вычисления поправок за центрировки и редукции мож-

но проследить по табл. 30, в которой вычисления даны на двух

пунктах. Для направлений остальных пунктов вычисленные по-

правки приведены в табл. 31.

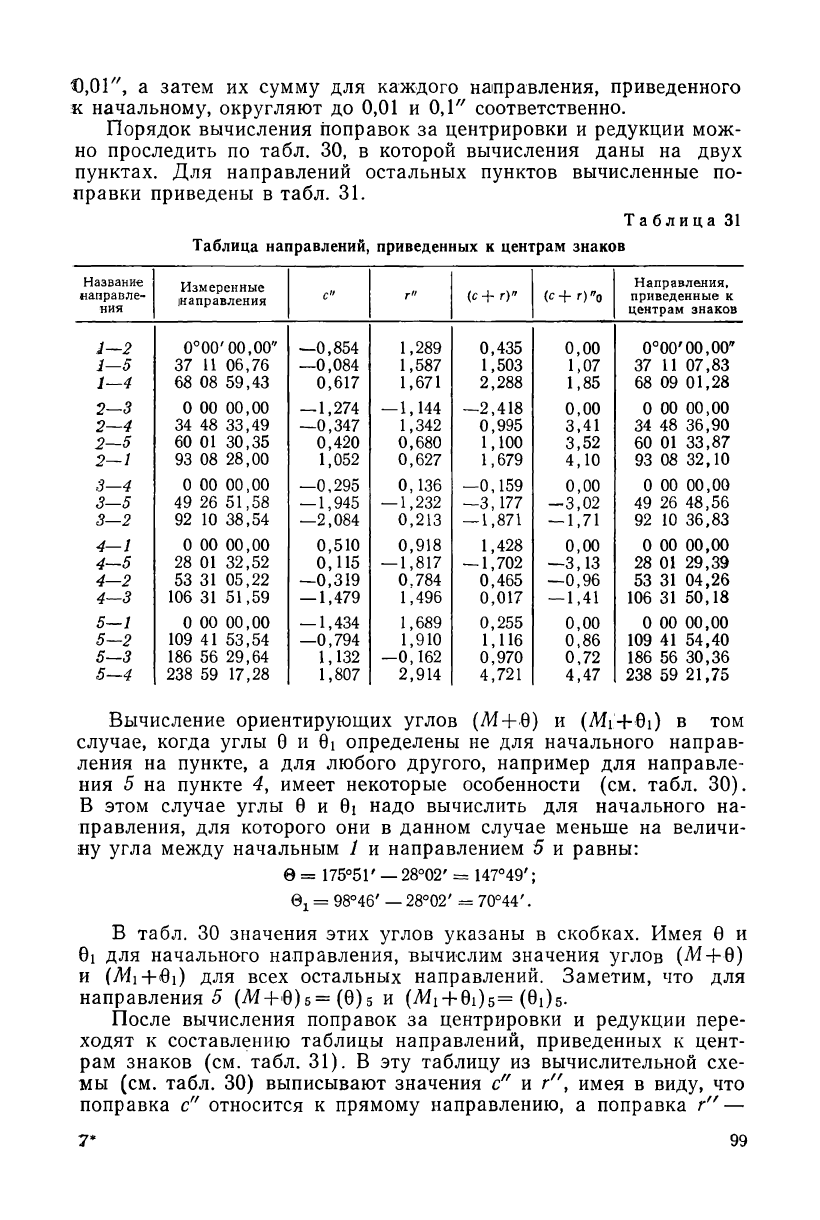
Таблица 31

Таблица направлений, приведенных к центрам знаков

Название

направле-

ния

Измеренные

(направления

с"

г"

(*+

г)"

(с+То

Направления,

приведенные к

центрам знаков

1—2

0°00'00,00*

—0,854 1,289

0,435 0,00

0°00'00,00"

1—5

37 И 06,76

—0,084

1,587

1,503 1,07

37 11 07,83

1—4

68 08 59,43

0,617

1,671

2,288

1,85

68 09 01,28

2-3

0 00 00,00

— 1,274 — 1,144 —2,418

0,00

0 00 00,00

2—4

34 48 33,49

—0,347

1,342

0,995 3,41

34 48 36,90

2-5

60 01 30,35

0,420

0,680 1,100 3,52

60 01 33,87

2-1

93 08 28,00

1,052

0,627

1,679

4,10

93 08 32,10

3—4

0 00 00,00

—0,295

0,136

—0,159 0,00

0 00 00,00

3—5

49 26 51,58

— 1,945

-1,232

—3,177

-3,02

49 26 48,56

3—2

92 10 38,54

—2,084 0,213

— 1,871

—1,71

92 10 36,83

4—1

0 00 00,00

0,510

0,918

1,428 0,00

0 00 00,00

4-5

28 01 32,52

0,115

— 1,817

—

1,702

—3,13

28 01 29,39

4—2

53 31 05,22

—0,319

0.784

0,465 —0,96

53 31 04,26

4—3 106 31 51,59

—

1,479

1,496

0,017 -1,41

106 31 50,18

5—1

0 00 00,00

—

1,434 1,689

0,255

0,00

0 00 00,00

5-2

109 41 53,54

—0,794

1,910

1,116 0,86 109 41 54,40

5—3 186 56 29,64

1,132

—0,162

0,970 0,72

186 56 30,36

5-4

238 59 17,28

1,807

2,914

4,721

4,47

238 59 21,75

Вычисление ориентирующих углов (Л4+.0) и

(Afi

+ 0i) в том

случае, когда углы G и 0i определены не для начального направ-

ления на пункте, а для любого другого, например для направле-

ния 5 на пункте 4, имеет некоторые особенности (см. табл. 30).

В этом случае углы 0 и 0i надо вычислить для начального на-

правления, для которого они в данном случае меньше на величи-

ну угла между начальным 1 и направлением 5 и равны:

0 = 175°5Г — 28°02' = 147°49';

= 98°46' — 28°02' = 70°44'.

В табл. 30 значения этих углов указаны в скобках. Имея 0 и

0i для начального направления, вычислим значения углов

(Л1

+ 0)

и (М1+61) для всех остальных направлений. Заметим, что для

направления 5 (М-Ь0)

=(0)

(Afi

+ 0i)

= (0i)s.

После вычисления поправок за центрировки и редукции пере-

ходят к составлению таблицы направлений, приведенных к цент-

рам знаков (см. табл. 31). В эту таблицу из вычислительной схе-

мы (см. табл. 30) выписывают значения с" и г", имея в виду, что

поправка с" относится к прямому направлению, а поправка г" —

к обратному. Так, например, поправки за центрировку, вычислен-

ные на пункте 7, вводятся в направления 1—2, 1—5, 1—4

а по-

правки за редукцию — в обратные направления: 2—/, 5—1

4—1.

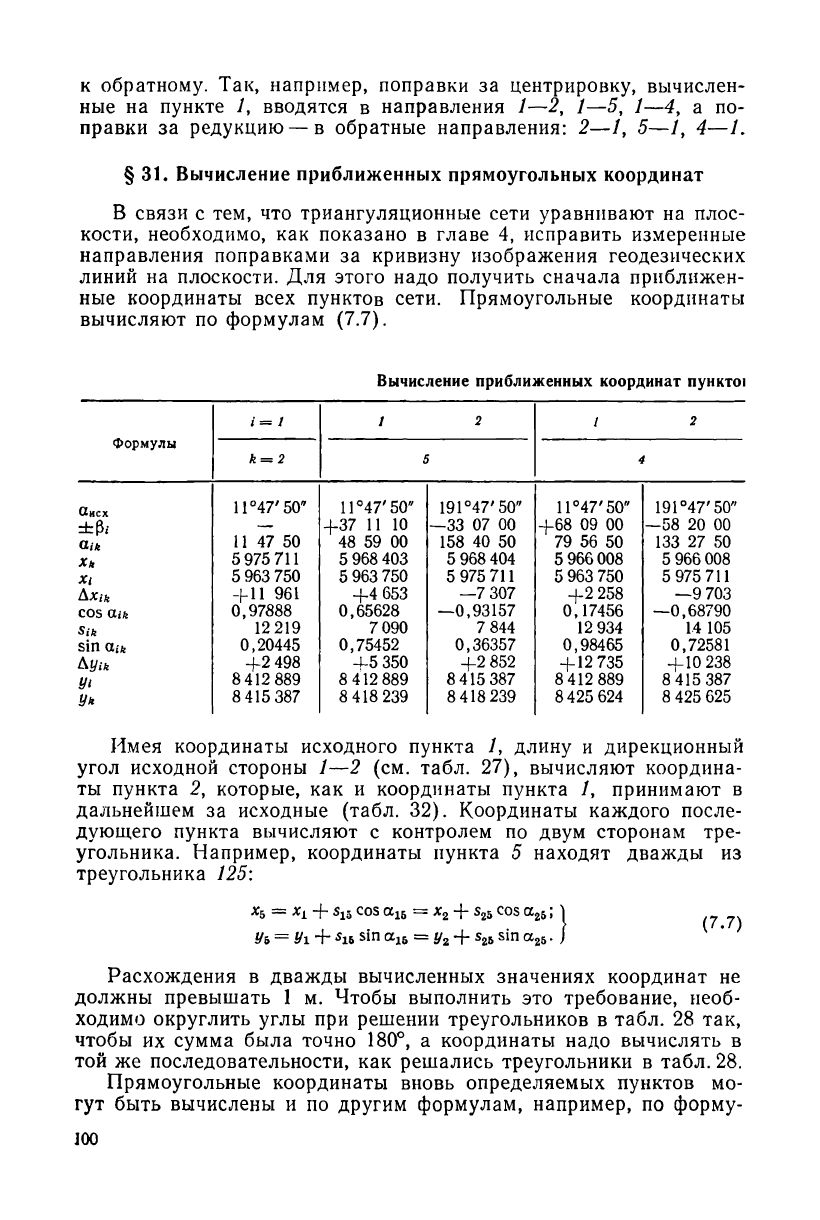
§ 31. Вычисление приближенных прямоугольных координат

В связи с тем, что триангуляционные сети уравнивают на плос-

кости, необходимо, как показано в главе 4, исправить измеренные

направления поправками за кривизну изображения геодезических

линий на плоскости. Для этого надо получить сначала приближен-

ные координаты всех пунктов сети. Прямоугольные координаты

вычисляют по формулам (7.7).

Вычисление приближенных координат пункто!

Формулы

i = I l

Формулы

k = 2

5 4

Оисх

U°4V 50" И^'бО"

191°47'50"

11°47'50"

191°47'50"

=fcpi

—

+37 11 10 —33 07 00

+68 09 00

—58 20 00

CLik

11 47 50

48 59 00 158 40 50

79 56 50

133 27 50

975

711

968

403

5 968 404

966

008

966

008

963

750

963

750

5 975 711

963

750

5 975 711

A Xik

+ 11 961

+4 653

—7 307

+2 258 —9 703

cos a ik

0,97888

0,65628

—0,93157

0,17456

—0,68790

Sik

12219

7 090 7 844

934 14 105

sin a ik

0,20445

0,75452

0,36357

0,98465

0,72581

A y

+2 498

4-5 350

+2 852

735

+10 238

412

889 8 412 889

415

387

8 412 889

8 415 387

Уь

415

387

8 418 239 8 418 239

425

624 8 425 625

Имея координаты исходного пункта /, длину и дирекционный

угол исходной стороны 1—2 (см. табл. 27), вычисляют координа-

ты пункта 2, которые, как и координаты пункта /, принимают в

дальнейшем за исходные (табл. 32). Координаты каждого после-

дующего пункта вычисляют с контролем по двум сторонам тре-

угольника. Например, координаты пункта 5 находят дважды из

треугольника 125:

= +

$15

OS«16 = *

+ S

cosa

; |

Уь = У1 + Sib sin а

хъ

= y

+ s

sin a

Расхождения в дважды вычисленных значениях координат не

должны превышать 1 м. Чтобы выполнить это требование, необ-

ходимо округлить углы при решении треугольников в табл. 28 так,

чтобы их сумма была точно 180°, а координаты надо вычислять в

той же последовательности, как решались треугольники в табл. 28.

Прямоугольные координаты вновь определяемых пунктов мо-

гут быть вычислены и по другим формулам, например, по форму-

100

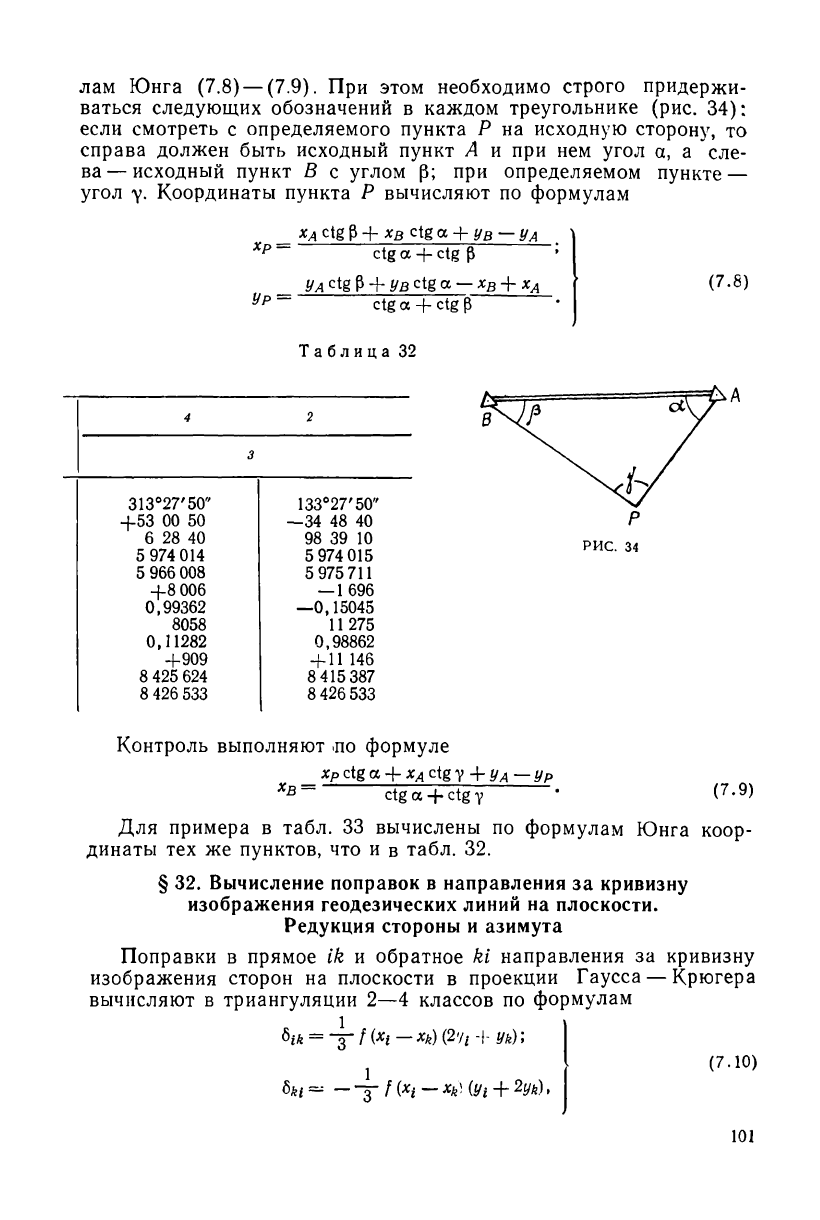
лам Юнга (7.8) — (7.9). При этом необходимо строго придержи-

ваться следующих обозначений в каждом треугольнике (рис. 34):

если смотреть с определяемого пункта Р на исходную сторону, то

справа должен быть исходный пункт А и при нем угол а, а сле-

ва— исходный пункт В с углом Р; при определяемом пункте —

угол у. Координаты пункта Р вычисляют по формулам

__ х

ctg

+ х

ctg а + у в

—

У л

Хр

- ctga + ctgft

ctg

+ У в ctg а

—

+ х

Ур

~ ctgoc + ctgp

(7.8)

Таблица 32

313°27'50"

+53 00 50

6 28 40

974

014

966

008

006

0,99362

8058

0,11282

+909

8 425 624

8 426 533

133°27'50"

—34 48 40

98 39 10

5 974 015

975

711

—

696

—0,15045

11275

0,98862

+ 11 146

415

387

8 426 533

Контроль выполняют ло формуле

ctga + x

ctgy +у

— у

ctg a + ctg у

(7.9)

Для примера в табл. 33 вычислены по формулам Юнга коор-

динаты тех же пунктов, что и в табл. 32.

§ 32. Вычисление поправок в направления за кривизну

изображения геодезических линий на плоскости.

Редукция стороны и азимута

Поправки в прямое ik и обратное ki направления за кривизну

изображения сторон на плоскости в проекции Гаусса — Крюгера

вычисляют в триангуляции 2—4 классов по формулам

« - — /

(**

— x

) (y

+ 2y

(7.10)

101

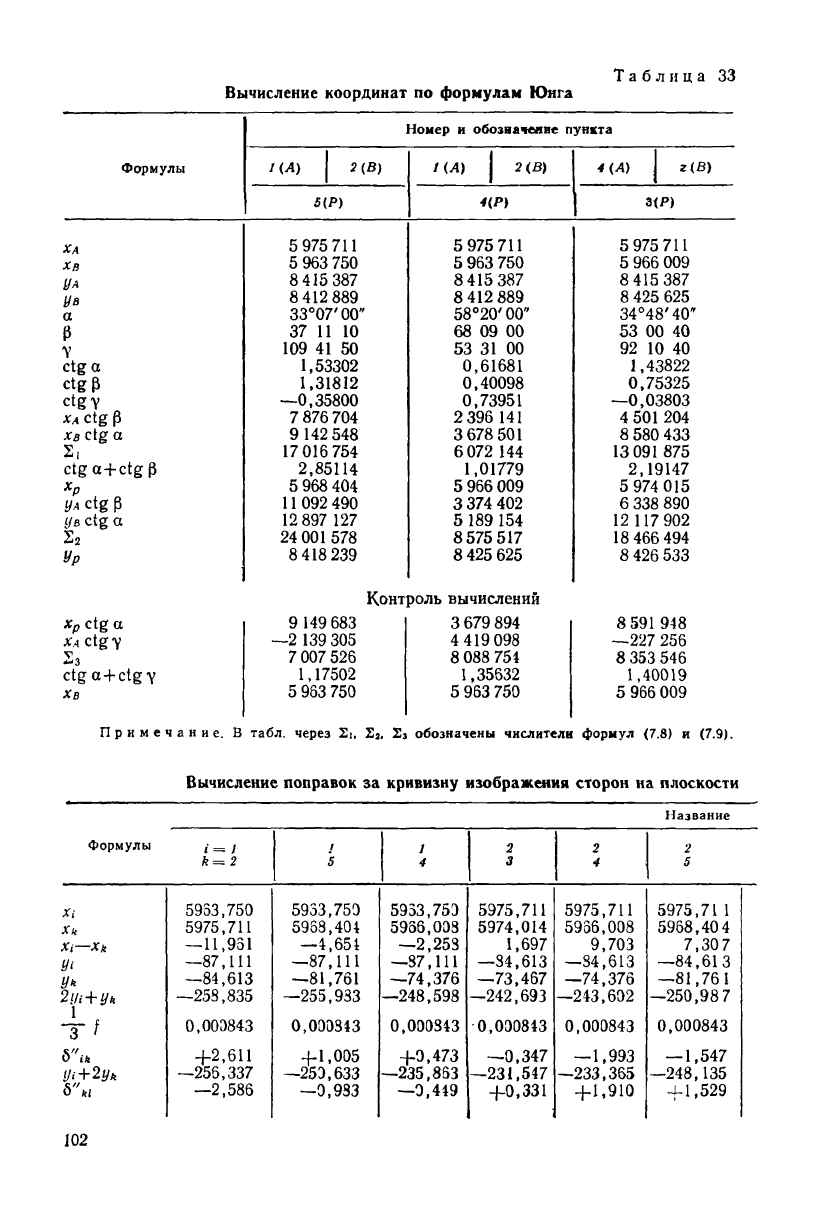
Таблица

Вычисление координат

по

формулам Юнга

Формулы

Номер

обозначение пункта

1(A)

2(B)

5(Р)

1(A)

2(B)

4(Р)

4(A)

г (В)

3 <Р)

X А

Хв

Уа

Ув

ctg а

ctgP

ctg у

Ctg р

Хв ctg a

ctga+ctgp

У л ctg p

if в ctg a

Ур

ctg a

ctg у

ctg a + ctg у

5 975 711

5 963 750

415

387

8 412 889

33°07'00"

37 11 10

109 41 50

1,53302

1,31812

—0,35800

7 876 704

142

548

016 754

2,85114

5 968 404

092 490

897 127

001

578

418

239

5 975 711

5 963 750

8 415 387

8 412 889

58° 20' 00"

68 09 00

53 31 00

0,61681

0,40098

0,73951

2 396 141

3 678 501

6072

144

1,01779

5 966 009

3 374 402

5 189 154

575

517

8 425 625

Контроль вычислений

149

683

-2

139

305

7 007 526

1,17502

963

750

3 679 894

4 419 098

8 088 754

1,35632

5 963 750

5 975 711

5 966 009

8 415 387

8 425 625

34°48'40"

53 00 40

92 10 40

1,43822

0,75325

—0,03803

501

204

8 580 433

13 091

875

2,19147

5 974 015

6 338 890

12 117 902

466 494

8 426 533

591

948

—227

256

353

546

1,40019

5 966 009

Примечание.

табл. через

обозначены числители формул

<7.8) и

(7.9).

Вычисление поправок

за

кривизну изображения сторон

на

плоскости

Название

Формулы

i= 1

k=2

Xi—Xk

2{П + Ун

5953,750

5975,711

—11,951

—87,111

—84,613

—258,835

5953,750

5953,404

—4,654

—87,111

—81,761

—255,933

5953,753

5956,003

—2,253

—37,111

—74,376

—248,598

5975,711

5974,014

1,697

—34,613

—73,467

—242,693

5975,711

5956,008

9,703

—34,613

—74,376

—243,602

5975,71

5968,404

7,307

—84,613

—81,761

—250,987

т'

0,00Э843

0,000343

0,000843

tji+2y

+2,611

—256,337

—2,586

+1,005

—25Э,633

—0,933

+0,473

—235,853

—0,449

—0,347

—231,547

+0,331

—1,993

—233,365

+1,910

— 1,547

—248,135

4-1,529

102

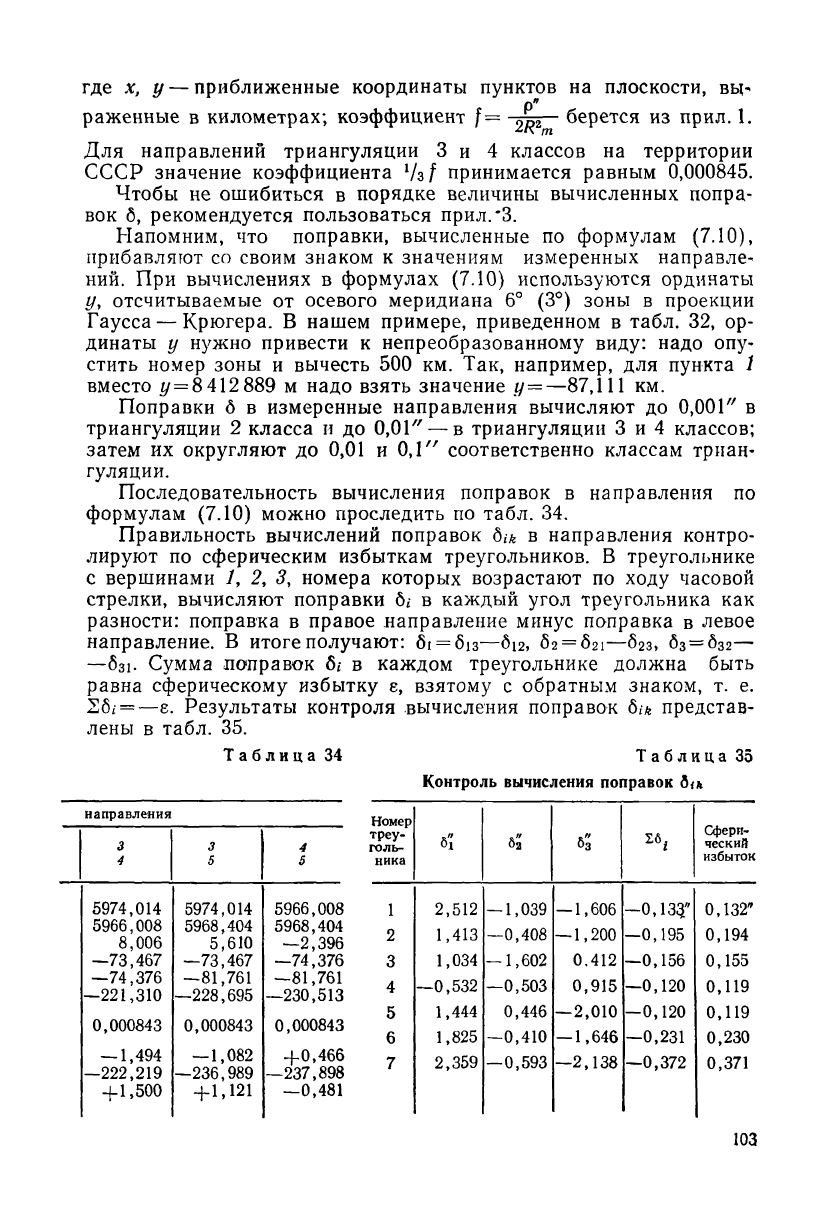
где х, у— приближенные координаты пунктов на плоскости, вы-

раженные в километрах; коэффициент f=

у>

берется из прил. 1.

пг

Для направлений триангуляции 3 и 4 классов на территории

СССР значение коэффициента 7з / принимается равным 0,000845.

Чтобы не ошибиться в порядке величины вычисленных попра-

вок б, рекомендуется пользоваться прил.'З.

Напомним, что поправки, вычисленные по формулам (7.10),

прибавляют со своим знаком к значениям измеренных направле-

ний. При вычислениях в формулах (7.10) используются ординаты

у, отсчитываемые от осевого меридиана 6° (3°) зоны в проекции

Гаусса — Крюгера. В нашем примере, приведенном в табл. 32, ор-

динаты у нужно привести к непреобразованному виду: надо опу-

стить номер зоны и вычесть 500 км. Так, например, для пункта 1

вместо # = 8 412 889 м надо взять значение у = —87,111 км.

Поправки 6 в измеренные направления вычисляют до 0,001" в

триангуляции 2 класса и до 0,01" — в триангуляции 3 и 4 классов;

затем их округляют до 0,01 и 0,1" соответственно классам триан-

гуляции.

Последовательность вычисления поправок в направления по

формулам (7.10) можно проследить по табл. 34.

Правильность вычислений поправок б^ в направления контро-

лируют по сферическим избыткам треугольников. В треугольнике

с вершинами /, 2, 3, номера которых возрастают по ходу часовой

стрелки, вычисляют поправки 6* в каждый угол треугольника как

разности: поправка в правое направление минус поправка в левое

направление. В итоге получают:

= 613—612, 62 = 621—6

з> 63 = 632—

—631. Сумма поправок 6в каждом треугольнике должна быть

равна сферическому избытку е, взятому с обратным знаком, т. е.

26; = —е. Результаты контроля вычисления поправок 6ik представ-

лены в табл. 35.

Таблица 35

Контроль вычисления поправок 6ih

Таблица 34

направления

Номер

Сфери-

ческий

3 3

треу-

голь-

6з

хл

Сфери-

ческий

4 5

ника

избыток

5974,014

5974,014 5966,008

2,512

—

1,039 — 1,606

—0,135"

0,132"

5966,008

8,006

5968,404

5,610

5968,404

—2,396

1,413

—0,408

— 1,200 —0,195

0,194

—73,467 —73,467 —74,376

1,034

—

1,602

0,412

—0,156

0,155

—74,376

—221,310

—81,761

—228,695

—81,761

—230,513

—0,532

—0,503

0,915

—0,120

0,119

—81,761

—228,695

—81,761

—230,513

1,444

0,446

—2,010 —0,120

0,119

0,000843

1,444

0,446

—2,010

—0,231

0,119

0,000843

1,825 —0,410

— 1,646 —0,231

0,230

— 1,494

—222,219

—1,082

—236,989

+0,466

—237,898

2,359

—0,593 —2,138

—0,372

0,371

+ 1,500

+ 1,121

—0,481

103

Редукция длины исходной стороны и переход

от геодезического азимута к дирекционному углу

Редуцирование исходной стороны S\

с эллипсоида на плос-

кость выполняют в триангуляции 2 класса по формуле

s = S + = S + + (7.11)

где /' =

= = Л-

В формуле (7.11) ординаты у концов стороны отсчитываются

от осевого меридиана зоны и выражаются в километрах; значения

коэффициента f выбираются из прил. 1 по средней широте триан-

гуляции, длина стороны S задается в метрах.

В табл. 36 в качестве примера даны вычисления редукции дли-

ны исходной стороны триангуляции с эллипсоида на плоскость. Из

этой таблицы видно, что влияние второго члена в скобках форму-

лы (7.11) на величину поправки As практически равно нулю, так

как приращение ординат Ду = 2,5 км в данном случае незначи-

тельно.

Таблица 36

Редукция исходной стороны 1—2 с эллипсоида на плоскость

Элементы формулы

Численные значения Элементы формулы

Численные

значения

Si, 2, м

Уи КМ

У2

Ут

217,45

—87,111

—84,613

—85,862

2,498

1,22665-10-8

At/2/12

= rS

Sl2 = £

+ AS

7372,3

0,5

7372,8

1,10

12 218,55 м

В случае когда задан геодезический азимут исходной стороны

А12 на поверхности эллипсоида, необходимо перейти от него к ди-

рекционному углу этой стороны на плоскости. В качестве примера

вычислим по формуле (4.5) дирекционный угол исходной стороны

У—2, взяв ее геодезический азимут /4I

= 10

43'49,254" из табл. 27.

Поправка за кривизну изображения стороны на плоскости вычис-

лена по формуле (7.10) в табл. 34 и оказалась равной 612=

= +2,611". Гауссово сближение меридианов у

вычисленное по

формуле (5.15), приведено в табл. 27 и равно

= — 1°03'59,935".

С этими данными получим

Л12 — Yi

612

= 10°43'49,254" + 1°03'59,935" + 2,61 Г = 11°47'51,80".

§ 33. Составление сводки направлений, приведенных

к центрам знаков и редуцированных на плоскость

Вычислив поправки за кривизну изображения сторон на плос-

кости, исправим ими измеренные направления. В итоге получим

сводку измеренных направлений, приведенных к центрам знаков

и редуцированных на плоскость в проекции Гаусса — Крюгера

(табл. 37).

Составление такой сводки является заключительным этапом

предварительных вычислений. Сводка редуцированных на плос-

кость направлений является исходным документом при уравнива-

нии триангуляции и должна быть составлена безошибочно. Одна-

ко в ней могут скрываться ошибки, допущенные на каком-либо

Таблица 37

Сводка измеренных и уравненных направлений на плоскости

Номер

пункта

Номер

направ-

ления

Направле-

ния, приве-

денные к

центрам зна-

ков

6"—6Q

Направле-

ния на пло-

скости

Поправки

из уравни-

вания

Уравненные

направления

4 1

1 5

7 8

0°00'00,00"

37 11 07,83

68 09 01,28

2,611"

1,005

0,473

0,00

—1,61

—2,14

00,00"

06,22

59,14

—0,10"

0,41

-0,31

(

W00,00"

11 06,73

08 58,93

0 00 00,00

34 48 36,90

60 01 33,87

93 08 32,10

—0,347

— 1,993

— 1,547

—2,586

0,00

-1,65

— 1,20

—2,24

00,00

35,25

32,67

29,86

—0,50

0,24

0,42

—0,15

00 00,00

48 35,99

01 33,59

08 30,21

0 00 00,00

49 26 48,56

92 10 48,56

—

1,494

—

1,082

0,331

0,00

0,41

1,82

00,00

48,97

38,65

—0,06

-0,11

0,17

00 00,00

26 48,92

10 38,88

4 И

0 00 00,00

28 01 29,39

53 31 04,26

106 31 50,18

—0,449

0,466

1,910

1,500

0,00

0,92

2,36

1,95

106

00,00

30,31

06,62

52,13

0,00

—0,07

0,23

-0,15

106

00 00,00

01 30,24

31 06,85

31 51,98

0 00 00,00

109 41 54,40

186 56 30,36

238 59 21,75

-0,933

1,529

1,121

—0,481

0,00

2,51

2,10

0,50

109

186

238

00,00

56,91

32,46

22,25

—0,14

—0,40

0,50

0,05

109

186

238

00 00,00

41 56,65

56 33,10

59 22,44

этапе предварительных вычислений. Например, незамеченная гру-

бая ошибка в длине стороны отразится на величине поправок за

центрировку и редукцию соответствующих направлений, а следо-

вательно, и на численных значениях самих направлений. Поэтому

все предварительные вычисления, начиная с проверки полевых

журналов и кончая составлением сводки направлений на плоско-

сти, должны выполняться особо аккуратно и тщательно, в две

руки.

Сводку направлений заполняют в такой последовательности:

сначала в нее записывают все связанное с получением редуциро-

ванных на плоскость направлений (графы 1—6), а затем, по окон-

чании уравнительных вычислений, заполняют графы 7 и 8. Таким

образом, сводка содержит как измеренные, так и уравненные на-

правления.

105

§ 34. Определение допустимых величин свободных членов

условных уравнений

Прежде чем приступить к уравниванию триангуляции за возни-

кающие в ней геометрические условия, необходимо убедиться, что

угловые измерения исполнены качественно и удовлетворяют по

точности предъявляемым к ним требованиям. С этой целью срав-

нивают вычисленные свободные члены условных уравнений с уста-

новленными для них допусками.

В общем случае предельную величину свободного члена услов-

ного уравнения

iVi + a

-f- w =

находят по формуле

= (7.12)

где

(LI

— средняя квадратическая ошибка единицы веса, t — пара-

метр, зависящий при заданной доверительной вероятности от чис-

ла измерений в сети, [аа] — сумма квадратов коэффициентов ус-

ловного уравнения.

В геодезических сетях при доверительной вероятности 0,95 при-

нимают / = 2,5. При уравнивании углов ошибку единицы веса бе-

рут равной средней квадратической ошибке измеренного угла для

соответствующего класса триангуляции.

Среднюю квадратическую ошибку измеренного угла вычисляют

по невязкам треугольников

j/ 2ш

m==

У ~~3п~*

где Ъш

— сумма квадратов невязок треугольников, п — число не-

вязок треугольников.

Невязки треугольников вычисляют по углам, приведенным к

центрам знаков,

w = 20 — (180° + е)

—

на сфере,

w = 20 — 180° — на плоскости,

где — сумма измеренных углов в треугольнике, е— сферичес-

кий избыток треугольника.

При нормальном законе распределения ошибок 67% невязок

должны находиться в интервале от 0 до т|3, 95%—от 0 до

2,5т]/3 и только три невязки из тысячи могут быть допущены рав-

ными 3m}/3.

Средние квадратические ошибки измеренного угла т, вычис-

ленные по невязкам треугольников, должны быть в триангуляции

1, 2, 3 и 4 классов не более 0,7; 1; 1,5 и 2" соответственно. Пре-

дельные невязки треугольников, вычисленные по формуле

о>фиг = 2,5т" /3, (7.13)

не должны превышать 3, 4, 6 и 8" в триангуляции 1, 2, 3 и 4 клас-

сов соответственно.

106

Свободные члены полюсных условий в геодезических четырех-

угольниках и центральных системах должны быть не более

а>пол = 2,5т" /gc(7.14)

где 2 ctg

p — сумма квадратов котангенсов связующих углов тре-

угольников, т" — средняя квадратическая ошибка измерения уг-

лов.

Значения свободных членов базисного и азимутального усло-

вий не должны превышать величин, вычисленных по формулам;

для базисного условия (в метрах)

^баз = 2,5 у^т»)

2 Ctg

р + 2тV (7.15)

для азимутального условия

о>аз = 2,5 |/"т"

л + 2т

а, (7.16)

где 2ctg

p — сумма квадратов котангенсов связующих углов тре-

угольников, т" — средняя квадратическая ошибка измерения уг-

лов в триангуляции данного класса, Ь

— длина базисной (жест-

кой) стороны на втором конце ряда треугольников, ть и т

—

средние квадратические ошибки базисных сторон и исходных ази-

мутов (дирекционных углов) соответственно, п — число углов в

передаче азимута.

Если свободный член какого-либо условного уравнения не удов-

летворяет установленным допускам, то такое уравнение включать

в уравнивание сети нельзя до тех пор, пока не будут выявлены и

устранены причины, приведшие к недопустимой величине свобод-

ного члена данного условного уравнения.

Часть IV

УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ

НА ПЛОСКОСТИ

В ПРОЕКЦИИ ГАУССА— КРЮГЕРА

Глава 8

УРАВНИВАНИЕ СВОБОДНОЙ ТРИАНГУЛЯЦИИ

КОРРЕЛАТНЫМ СПОСОБОМ

§ 35. Общие сведения по уравниванию триангуляции

Для уравнивания триангуляции применяют как коррелатный,

так и параметрический способы. В обоих случаях уравнивание се-

ти выполняется под одним и тем же условием метода наименьших

квадратов 2p^

= min, где v — поправки из уравнивания к непо-

средственно измеренным величинам с весом р. С этой точки зре-

ния оба способа являются эквивалентными и приводят к одним

и тем же значениям уравненных элементов сети.

Однако при уравнивании конкретных сетей триангуляции вы-

бирают тот способ, который по технико-экономическим соображе-

ниям оказывается более выгодным. Например, большие или ма-

лые, но сложные по построению сети с большим числом избыточ-

ных диагоналей или сети с большим числом исходных пунктов

проще уравнивать параметрическим способом, особенно при ис-

пользовании ЭВМ. При уравнивании небольших и несложных се-

тей часто применяют коррелатный способ.

Для того чтобы можно было вычислить на плоскости прямо-

угольные координаты всех пунктов геодезической сети, необходи-

мо в качестве исходных иметь как минимум четыре элемента: ко-

ординаты одного пункта (х, у), а также длину и дирекционный

угол исходной стороны (s и а) или, что все равно, координаты

двух пунктов на концах исходной стороны.

Геодезическая сеть, в которой заданы координаты только двух

пунктов, находящихся на концах исходной стороны, называется

свободной; сеть, в которой кроме двух исходных пунктов имеются

и другие пункты с заданными (твердыми) координатами, называ-

ется несвободной.

Триангуляционные сети уравнивают как по направлениям, так

и по углам. С точки зрения принципа наименьших квадратов из

уравнивания следует определять поправки к непосредственно из-

108