Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

Глава 9

УРАВНИВАНИЕ НЕСВОБОДНОЙ ТРИАНГУЛЯЦИИ

КОРРЕЛАТНЫМ СПОСОБОМ

§ 41. Последовательность уравнивания несвободной сети

Характерной особенностью несвободной сети триангуляции яв-

ляется наличие в ней избыточного числа исходных пунктов с за-

данными координатами. Так как положение любого пункта на

плоскости определяется двумя координатами (х, у), то каждый

РИС. 39

избыточный исходный пункт доставляет два дополнительных ус-

ловных уравнения. Вид этих уравнений зависит от схемы взаимно-

го расположения исходных пунктов. В одних случаях могут возник-

нуть условия базисные (сторон), в других — условия дирекцион-

ных углов (сумм углов), в третьих — условия абсцисс и ординат.

Может оказаться и так, что все эти условия возникнут в сети од-

новременно.

Технологию уравнивания несвободной триангуляции проследим

на примере небольшой сети, изображенной на рис. 39. Список ко-

ординат исходных пунктов и сводка измеренных направлений,

приведенных к центрам знаков и редуцированных на плоскость,

даны в табл. 49 и 50.

В состав уравнительных вычислений в несвободной триангуля-

ции входит: определение числа и вида независимых условных

уравнений, составление условных уравнений и весовых функций,

составление и решение нормальных уравнений коррелат, вычисле-

ние поправок направлений, окончательное решение треугольников,

вычисление окончательных координат пунктов, оценка точности

уравненных элементов сети, составление каталога координат.

9-2296

129

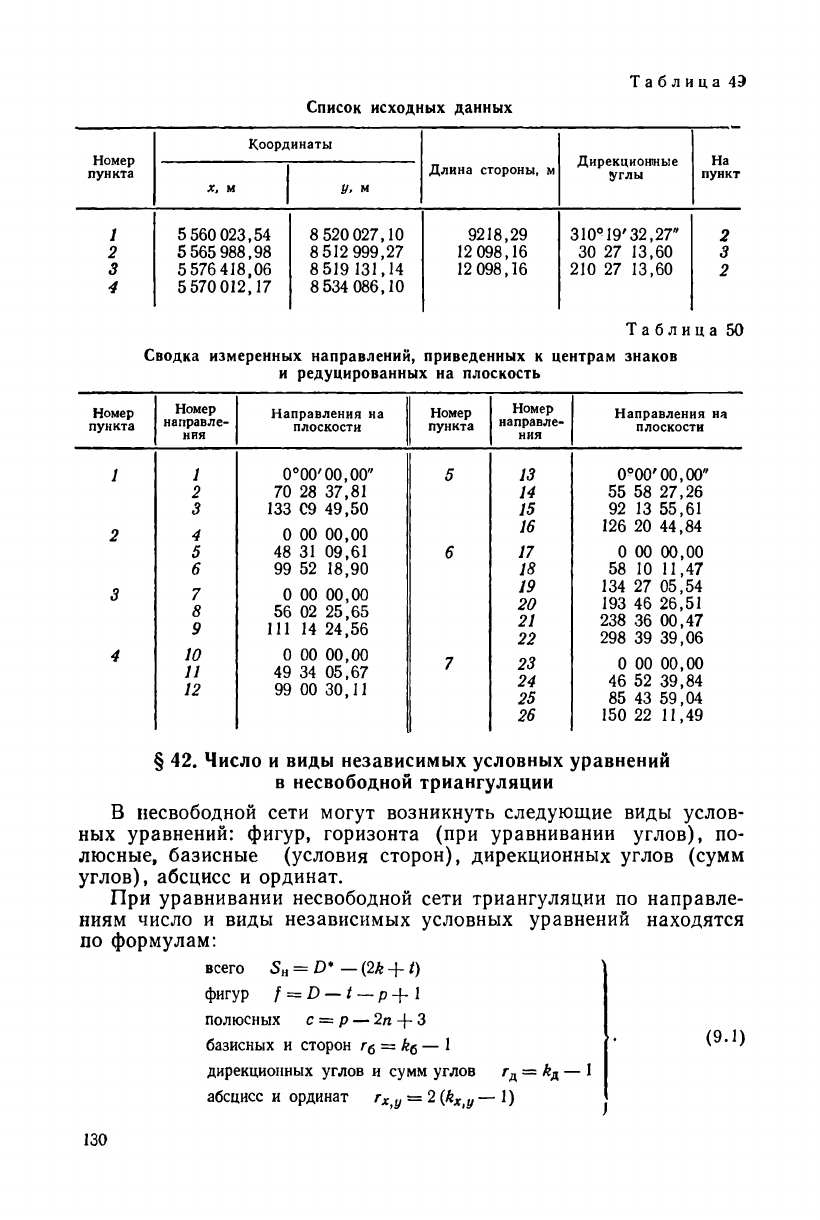
Таблица 78'

Список исходных данных

Номер

пункта

Координаты

Дирекциоюные

•углы

На

пункт

Номер

пункта

X, м

у,

Длина стороны, м

Дирекциоюные

•углы

На

пункт

5 560 023,54

5 565 988,98

5 576418,06

5 570 012,17

8 520 027,10

8 512 999,27

8519 131,14

8 534 086,10

9218,29

12 098,16

310°19'32,27"

30 27 13,60

210 27 13,60

Таблица 50

Сводка измеренных направлений, приведенных к центрам знаков

и редуцированных на плоскость

Номер

пункта

Номер

направле-

ния

Направления на

плоскости

Номер

пункта

Номер

направле-

ния

Направления на

плоскости

0°00'00,00"

13 0^00'00,00"

70 28 37,81

14 55 58 27,26

133 C9 49,50 15

92 13 55,61

0 00 00,00

126 20 44,84

48 31 09,61

0 00 00,00

6 99 52 18,90

58 10 11,47

0 00 00,00

56 02 25,65

111 14 24,56

134 27 05,54

193 46 26,51

238 36 00,47

298 39 39,06

0 00 00,00

49 34 05,67

99 00 30,11

0 00 00,00

46 52 39,84

85 43 59,04

150 22 11,49

§ 42. Число и виды независимых условных уравнений

в несвободной триангуляции

В несвободной сети могут возникнуть следующие виды услов-

ных уравнений: фигур, горизонта (при уравнивании углов), по-

люсные, базисные (условия сторон), дирекционных углов (сумм

углов), абсцисс и ординат.

При уравнивании несвободной сети триангуляции по направле-

ниям число и виды независимых условных уравнений находятся

по формулам:

всего S

= D* — (2k + t)

фигур / = D — t — p + 1

полюсных с = p — 2n + 3

базисных и сторон г

= —1 ' (9-1)

дирекционных углов и сумм углов Гд = — I

абсцисс и ординат г

y — 1)

-130

В формулах (9.1) обозначено: D* — общее число измеренных

в сети направлений (D), дополнительно измеренных (не вычис-

ленных по координатам) сторон (k

) и азимутов (i&a), вместе взя-

тых, т. е.

D* =D + k

+ ka; (9.2)

п — число всех пунктов в сети; k — число определяемых пунктов;

i — число пунктов, на которых исполнены угловые измерения;

р — число всех сторон в сети (исходных и определяемых); ke —

общее число исходных (в том числе вычисленных по координатам)

и дополнительно измеренных сторон; \k

— общее число исходных

(в том числе вычисленных по координатам) и дополнительно из-

меренных азимутов (дирекционных углов); \k

,y— число раздель-

ных групп исходных пунктов, не связанных между собой жестки-

ми сторонами. Отдельная группа может состоять либо из одного

пункта, либо из ряда смежных пунктов с заданными координата-

ми. Например, сеть триангуляции, изображенная на рис. 39, имеет

две раздельные группы исходных пунктов: в одну группу входят

три смежных пункта 2, <?, а во вторую— только один пункт 4.

Координатные условия возникают только в том случае, когда меж-

ду разными группами исходных пунктов имеется не менее двух

определяемых сторон.

Если в триангуляции нет дополнительно измеренных длин сто-

рон (k

= 0) и азимутов

(|fta

= 0), то в формулах (9.1) и (9.2) бу-

дет /)* = £), где D — число измеренных направлений.

При уравнивании несвободной триангуляции по углам число

независимых условных уравнений определяется по формулам:

всего Sy — N* — 2k ^

фигур f = N — р — q-\- I

горизонта q N +1 — D

полюсных с = р — 2я + 3 ,

(9.3)

базисных и сторон — — 1

дирекционных углов и сумм углов г

= £

— 1

абсцисс и ординат г

= 2 (k

Xty

— 1)

В формулах (9.3) дополнительно к обозначениям в формулах

(9.1) и (9.2) принято: Л/* — общее число всех измеренных в сети

углов (JV), дополнительно измеренных сторон (k

) и азимутов

([k

)> вместе взятых, т. е.

N*=*N + k

+ ka. (9.4)

Если в сети нет дополнительно измеренных длин сторон (£

= 0)

и азимутов (&

= 0), то в этом случае

JV*

JV.

Через D обозначено

число направлений, образующих все измеренные в сети углы.

В нашей сети (см. рис. 39), которая будет уравниваться по на-

правлениям, измерено 26 направлений (D = 26); дополнительно

измеренных длин сторон и азимутов нет (k

=&a =0). В сети семь

пунктов (п = 7)

из которых три определяемых

= 3), и 13 сторон

131

(р=13); угловые измерения исполнены на 7 пунктах (/ = 7); число

исходных сторон ks = 2, число исходных дирекционных углов &

=2;

в сети две раздельные группы исходных пунктов (k

= 2). С эти-

ми данными получим по формулам (9.1) следующее число неза-

висимых условных уравнений в сети:

всего S» = 26 — (2x3 + 7) = 13,

фигур / = 26 -7 — 13+ I =7,

полюсных с~ 13 — 2x7 + 3 = 2,

базисных (сторон) rg = 2 — 1 -: 1,

дирекционных углов (сумм углов) г

= 2 —

= 1,

абсцисс и ординат r

Xiy

— 2 (2 — 1) = 2.

Следует обратить внимание на особенность определения числа

независимых условных уравнений в сети, замкнутой исходными

сторонами, как, например, в сети, показанной на рис. 40.

В целях выбора независимых условных

U уравнений в подобных сетях, замкнутых ис-

ходными сторонами, рекомендуется одну из

исходных сторон принять как бы за опреде-

ляемую. Другими словами, следует допус-

тить, что длина и дирекционный угол одной

исходной стороны якобы неизвестны, и в

jj соответствии с этим уменьшить число ба-

зисных условий и число условий дирекци-

онных углов каждое на одну единицу. Для

этого в формулах (9.1) и (9.3) надо вместо

и £д принять их новые значения: =

= кб—1,

&'д

= £д—1, оставив все остальные величины в этих фор-

мулах без изменений.

Для сети, изображенной на рис. 40, имеет: D=16, N=12, р = 8,

п = 5, k

—

t=5, йб = 4,

= 4, k

=l.

Приняв &6

=/z6—1=3; &д'=|&

—1=3 и полагая, что в сети бу-

дут уравниваться углы, определим по формулам (9.3) число и ви-

ды независимых условных уравнений в ней:

всего S

= 12 — 2x1 = Ю,

фигур /=12 —1—8+1=4,

горизонта g=I2 + 5 — 16=1,

полюсных с = 10 + 3= 1,

базисных Гб = (4 — 1) — 1 = 2,

дирекционных углов г

=(4 — i) —

= 2.

§ 43. Составление условных уравнений

и функций уравненных элементов

В несвободной сети, изображенной на рис. 39, при уравнивании

направлений возникает, как было подсчитано в § 42, всего 13 ус-

ловных уравнений: фигур 7, полюсных 2, базисных 1, дирекцион-

ных углов 1 и координатных 2.

Условные уравнения фигур возникают в трех треугольниках

геодезического четырехугольника и в тех четырех треугольниках

132

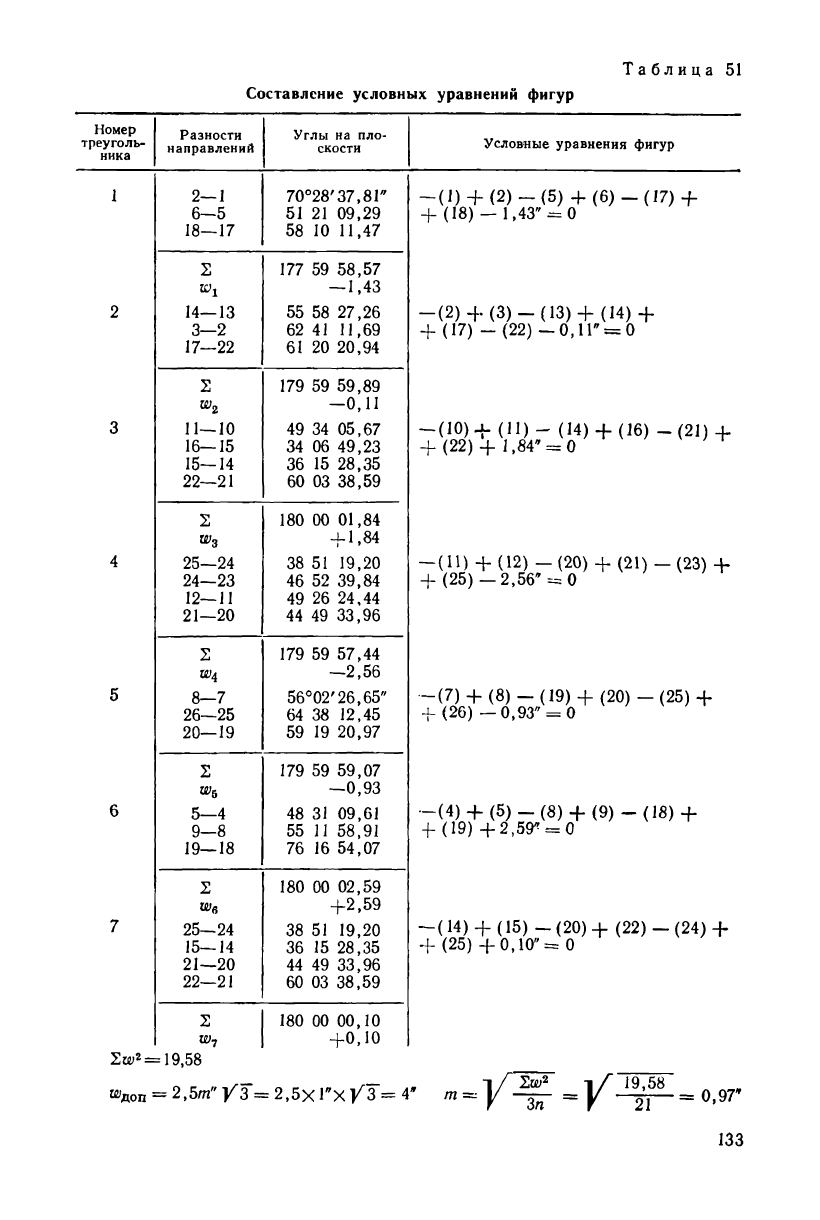
Таблица 78'

Составление условных уравнений фигур

Номер

треуголь-

ника

Разности

направлений

Углы на пло-

скости

Условные уравнения фигур

2—1

6-5

18—17

70°28'37,81"

51 21 09,29

58 10 11,47

-(1) + (2)-(5) + (6)-(17) +

+ (18) — 1,43" = 0

14—13

3-2

17—22

177 59 58,57

— 1,43

55 58 27,26

62 41 11,69

61 20 20,94

-(2)+ (3)-(13) +(14) +

+ (17) - (22) -0,П" = 0

11—10

16-15

15—14

22—21

179 59 59,89

—0,11

49 34 05,67

34 06 49,23

36 15 28,35

60 03 38,59

-(10)+(11)- (14)+ (16) -(21) +

+ (22) + 1,84" = 0

25—24

24—23

12—11

21—20

180 00 01,84

+ 1,84

38 51 19,20

46 52 39,84

49 26 24,44

44 49 33,96

-(11) + (12) - (20) + (21) - (23) +

+ (25)-2,56" = 0

8—7

26—25

20—19

179 59 57,44

—2,56

56°02'26,65"

64 38 12,45

59 19 20,97

-(7)+ (8)-(19)+ (20)-(25) +

+ (26) — 0,93" = 0

5-4

9-8

19—18

179 59 59,07

—0,93

48 31 09,61

55 И 58,91

76 16 54,07

-(4)+ (5)-(8)+ (9)-(18) +

-f (19) +2,59^ = 0

25-24

15-14

21—20

22—21

180 00 02,59

+2,59

38 51 19,20

36 15 28,35

44 49 33,96

60 03 38,59

-(14) + (15) - (20) + (22) - (24) +

+ (25) +0,10"= 0

180 00 00,10

+0,10

2а;

= 19,58

^on = 2,5m^3 = 2,5xl"x/3W m =

J^L

= 0>

9Г

-133

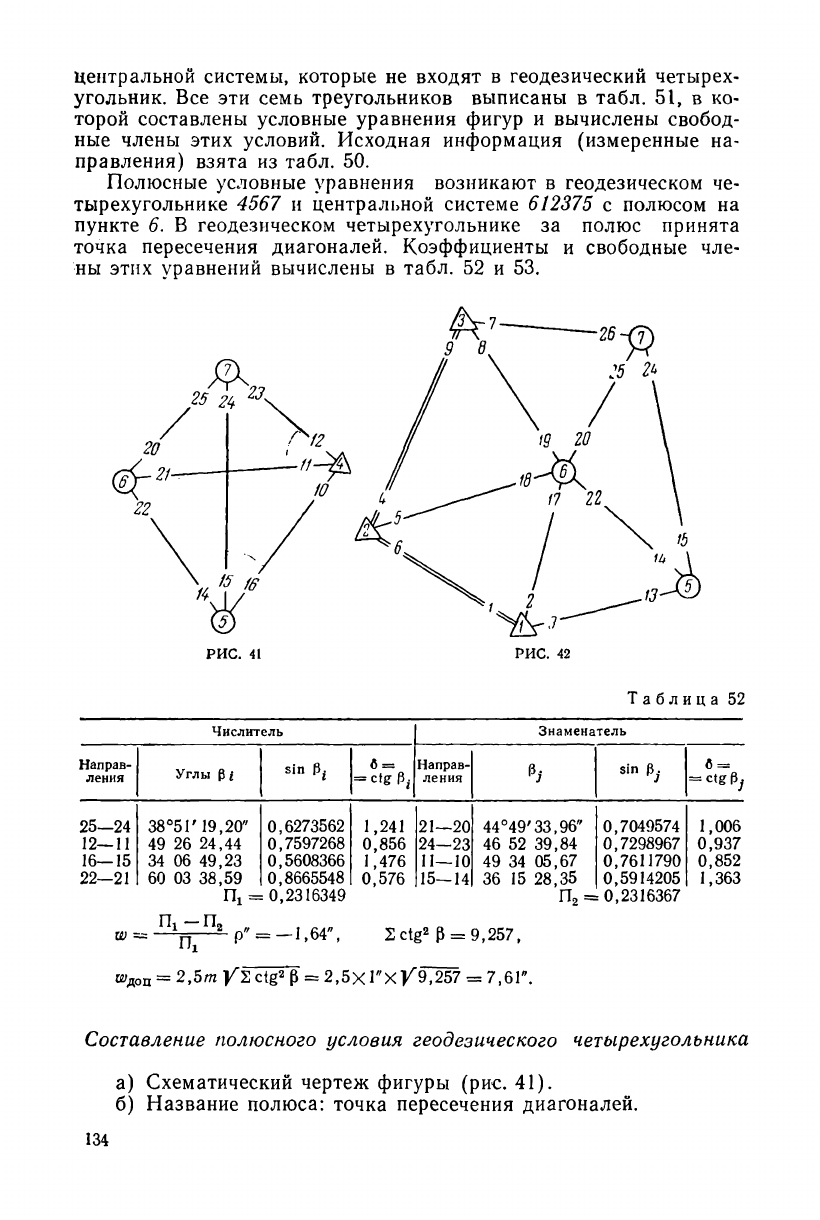
центральной системы, которые не входят в геодезический четырех-

угольник. Все эти семь треугольников выписаны в табл. 51, в ко-

торой составлены условные уравнения фигур и вычислены свобод-

ные члены этих условий. Исходная информация (измеренные на-

правления) взята из табл. 50.

Полюсные условные уравнения возникают в геодезическом че-

тырехугольнике 4567 и центральной системе 612375 с полюсом на

пункте 6. В геодезическом четырехугольнике за полюс принята

точка пересечения диагоналей. Коэффициенты и свободные чле-

ны этих уравнений вычислены в табл. 52 и 53.

Таблица 52

Числитель

Знаменатель

Направ-

ления

Углы

sin fL

6 =

= ctg Р.

Направ-

ления

sin fy

6 =

- ctg

25—24

12—11

16—15

22—21

38°5Г19,20"

49 26 24,44

34 06 49,23

60 03 38,59

0,6273562

0,7597268

0,5608366

0,8665548

1,241

0,856

1,476

0,576

21—20

24—23

11—10

15—14

44°49'33,96"

46 52 39,84

49 34 05,67

36 15 28,35

0,7049574

0,7298967

0,7611790

0,5914205

1,006

0,937

0,852

1,363

= 0,2316349 П

= 0,2316367

** \

П2 Р

= 2 Ctg2 Р = 9)257

on = 2,5m /2 ctg

P = 2,5x ГX /9^257 = 7,61".

Составление полюсного условия геодезического четырехугольника

а) Схематический чертеж фигуры (рис. 41).

б) Название полюса: точка пересечения диагоналей.

134

в) Полюсное условие, выраженное через синусы углов:

sin

(25

—

24)

sin

(12

—

11)

sin

(16

—15) sin

(22

— 27) __

sin

(21

— 20) sin —

23)

sin

(11

—

10)

sin

(15

—

14)

г) Вычисление свободного члена и коэффициентов x = ctgp при

поправках в измеренные направления (табл. 52).

д) Линейный вид условия:

«11-Ю (Ю) - [«li-to + «1

-ц] (П) + б

(12) + 6

(14) -

— [«15-14 + «16-15] (15) + «16-1Б (15) + «21-20 (20) - [в» -20 211 (21) +

+ 6

(22) + 6

З (23) - [6

З + 6

] (24) + 6

2б

(25) + ш = 0

или с учетом 6 = ctg р

+0,852 (10) — 1,708 (11) + 0,856 (12) + 1,363 (14) —

— 2,839 (15) + 1,476 (16) + 1,006 (20) — 1,582 (21) + 0,576 (22) +

+ 0,937 (23) — 2,178 (24) + 1,241 (25) — 1,64" « 0.

Составление полюсного условия центральной системы

а) Схематический чертеж фигуры (рис. 42).

б) Название полюса: пункт 6.

в) Полюсное условие, выраженное через синусы углов:

sin

—

sin

— 7) sin

(25

—

24)

sin

(14

—

13)

sin

—

sin

—

sin

(26

—

25)

sin

(15

—14) sin (5 —

sin

—

•

г) Вычисление свободного члена и коэффициентов

= ctg р при

поправках в измеренные направления (табл. 53).

Таблица 53

Числитель Знаменатель

Направ-

ления

Углы

sin |3.

б =

= ctg 0.

Направ-

ления

Углы fij

sin fly

= ctg fy

5—4

8—7

25—24

14—13

2—1

48°ЗГ09,6Г

56 02 25,65

38 51 19,20

55 58 27,26

70 28 37,81

0,7491793

0,8294322

0,6273562

0,8287861

0,9425084

0,884

0,673

1,241

0,675

0,355

9—8

26—25

15—14

3—2

6-5

55°1Г 58,91"

64 38 12,45

36 15 28,35

62 41 11,69

51 21 09,29

0,8211462

0,9036105

0,5914205

0,8885098

0,7810039

0,695

0,474

1,363

0,516

0,800

Г^ = 0,3045149 П

= 0,3045184

П1

П2

р" = — 2,38", 2ctg

Р = 6,828,

а/доп = 2,5 ш" /2ctg

P = 2,5х ГхКМ28 = 6,53".

д) Линейный вид условия:

«2~1 (1) + [«2-1 + «з-

] (2) - «3-2 (3) - «5-4 (4) + [«6-4 + «в-б] (5) -

- 6

(6) - 6

(7) + [6

+ 6

] (8) - 6

(9) - 6

(13) +

+ [«14-13 + «15-141 (14) ~ «15-14 (15) -«25-24 (24) +

+ [«25-24 + «26-25] (25) — 6

2в

(26) +

= 0.

135

или с учетом

= ctgP

—0,355 (1) + 0,871 (2) — 0,516 (3) — 0,884 (4) + 1,684 (5) - 0,800 (6) -

_ 0,673 (7) + 1,368 (8) —0,695 (9) - 0,675 (13) + 2,038 (14) — 1,363 (15) —

- 1,241 (24) + 1,715 (25) — 0,474 (26) — 2,38" = 0.

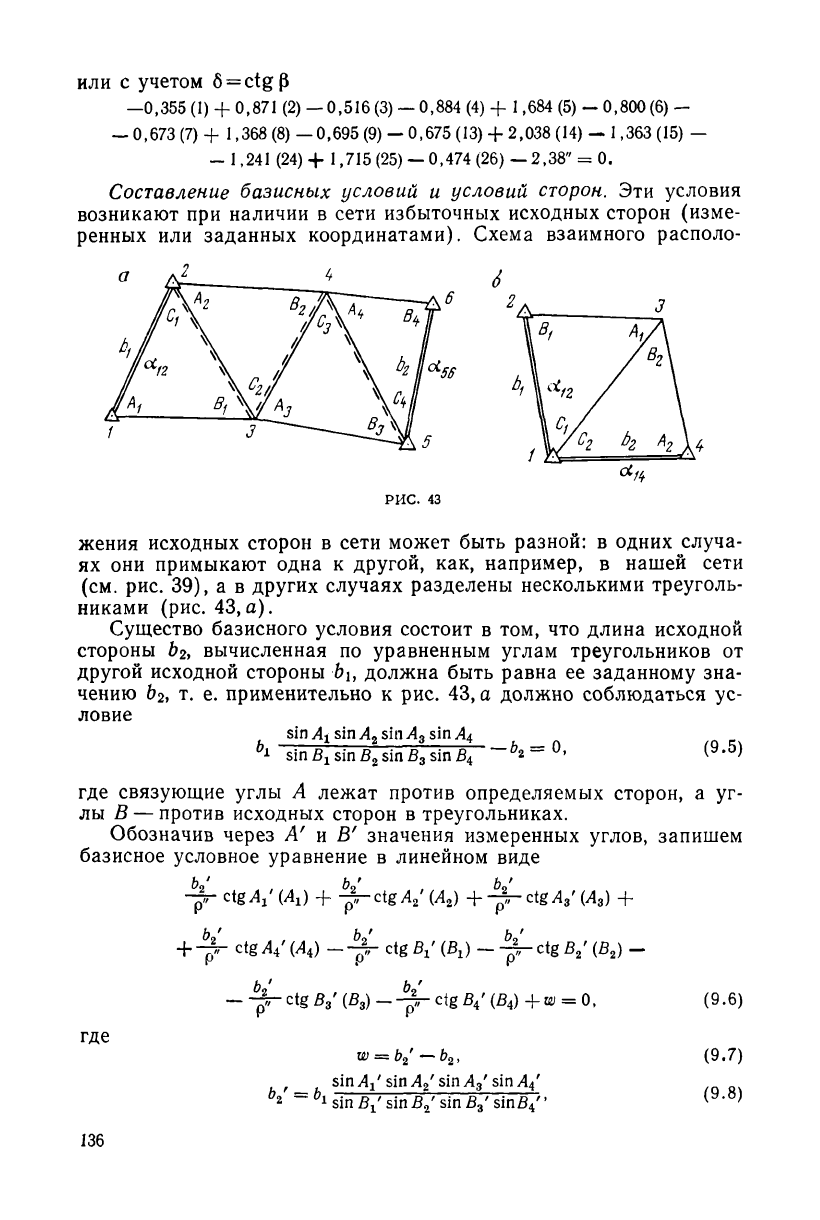
Составление базисных условий и условий сторон. Эти условия

возникают при наличии в сети избыточных исходных сторон (изме-

ренных или заданных координатами). Схема взаимного располо-

РИС. 43

жения исходных сторон в сети может быть разной: в одних случа-

ях они примыкают одна к другой, как, например, в нашей сети

(см. рис. 39), а в других случаях разделены несколькими треуголь-

никами (рис. 43,а).

Существо базисного условия состоит в том, что длина исходной

стороны й

, вычисленная по уравненным углам треугольников от

другой исходной стороны &ь должна быть равна ее заданному зна-

чению 6

> т. е. применительно к рис. 43, а должно соблюдаться ус-

ловие

sin

Ах

sin А

sin Л

* sin В

sin В

~~^ = (

)

где связующие углы А лежат против определяемых сторон, а уг-

лы В — против исходных сторон в треугольниках.

Обозначив через Л' и В' значения измеренных углов, запишем

базисное условное уравнение в линейном виде

ctg Л/Их) + (Л

) +-^r-ctgA

'(A

) +

+ ^г ctg Л

' (Л

) - ^г ctg В

* (BJ-^f- ctg В

' (В

) -

- ctg В

' (В

) - ctg В

' (В

) +

= 0, (9.6)

где

w = b

'-b

, (9.7)

, sin Ai sin A

sin A

sin sin B

sin B

sin£

136

—вычисленное по измеренным углам значение второй исход-

ной стороны

В целях удобства вычислений коэффициенты условных уравне-

ний выгодно иметь близкими к единице. С этой целью умножим

левую и правую части выражения (9.6) на р"\Ь'% и запишем ба-

зисное условное уравнение в окончательном виде:

ctg Л / (Л

) +

Ctg

' (Л

) + ctg Ла'

(Л

)

+ ctg А/

(Л

)

- ctg В/ (ВJ -

- ctg B

' (В

) - cig В

' (В

) - ctg В

' (В

) +

ш"

= 0, (9.9)

где свободный член выражен в секундах дуги:

(9.10)

В случае уравнивания сети по направлениям в выражении

(9.9) поправки в углы заменяются разностью поправок соответст-

вующих направлений.

В нашей сети (см. рис. 39) возникает базисное условие между

исходными сторонами

= Si

и b

= s

sin [2-1] sin 119-18]

12 sin [18 — 17] sin [9 — 5]

—

- I*-

где уравненные углы А я В выражены через разности направле-

ний.

Как и в полюсных условиях, введем обозначения вида ctgfi

—

= Ctg —i)=6*-i и запишем базисное условное уравнение (9.11)

в виде

-Vl (0 +

2-1 (2) + «9-8 (8) - «9-8 (9) + «18-17 0?) -

- [«18-17 + «19-18] (18) + «id-18 (19) + W" - 0, (9. 12)

где w" = (s'

— s

) ; (9.13)

вычисленное значение стороны s 23 равно

sin

—

sin

(19

—

18)

П1

s'23 =

12 sin

(18

—

17)

sin

—

(9.14)

Свободный член w выражен в секундах дуги.

Коэффициенты и свободный член базисного условного уравне-

ния (9.12) вычислены в табл. 54.

С учетом данных, приведенных в табл. 54, получим оконча-

тельный вид базисного условного уравнения:

—0,355 (1) + 0,355 (2) + 0,695 (8) — 0,695 (9) + 0,621 (17) -

— 0,865 (18) + 0,244 (19) + 2,05" = 0.

Составление условных уравнений дирекционных углов и сумм

углов. Условные уравнения этого вида возникают при наличии в

сети избыточных исходных дирекционных углов, заданных коорди-

натами пунктов или полученных на основе азимутальных опреде-

лений. Существо данного условия применительно, например к

137

Таблица 78'

Числитель

Знаменатель

Направ-

ления

Измеренные

углы fy

sin

6 =

= ctg fl.

Направ-

ления

Измеренные

углы Ру

sin

6 =

= ctg fy

2—1

19—18

70°28'37,8 Г

76 16 54,07

0,9425084

0,9714734

0,355

0,244

18-17

9-8

58°10' 11,47"

55 И 58,91

0,8496153

0,8211462

0,621

0,695

= 0,9156218 П

= 0,6976584

^12=9218,29 м, 523=

098,16 м, s'

= s

-^-=12098,28 м,

= (

- s

) = 2,05", 2 ctg

P = 1,054,

^доп==2.5 j/'m"

2 ctg

P + 2 P*)* «

/ / 2

V JO

= 2,5 у IX1.054 + 2 ( з$|ог] =3,48",

где принято ть1Ь=

: 300

ООО

и m"=l".

рис. 43, а, сводится к тому, что исходный дирекционный угол ссбв

одной стороны сети, вычисленный по уравненным углам треуголь-

ников от исходного дирекционного угла а\2 Другой стороны, дол-

жен быть равен заданному значению его ase, т. е.

—Ci + Cj —С

+С

± (п-1) 180°, (9.15)

где п — число промежуточных углов С, участвующих в передаче

дирекционного угла по ходовой линии, которая проходит через

вершины промежуточных углов треугольников (на рис. 43, а она

показана пунктиром).

Обозначив через С значения измеренных углов, а через (С) —

поправки к ним, напишем применительно к рис. 43, а условное

уравнение дирекционных углов в окончательном виде:

+ (С

) - (С

) + (С

) +

иг

= о, (9.16)

где w = а'

б6

—а

бв

, <х'

бв

= а

-С/ + С

' — С

' + С

' ± (л — 1) 180°.

Здесь а'бб — вычисленное по измеренным углам значение ди-

рекционного угла Обе-

Для сети, изображенной на рис. 43,6, условное уравнение ди-

рекционных углов, точнее, в данном случае условие суммы углов,

запишется в виде

+(Ci) +

)

= 0, (9.17)

где w = a'

— a

, <x'

= a

-f- С/ 4- С/.

В случае уравнивания направлений поправки углов выража-

ются через разности поправок направлений.

-138