Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

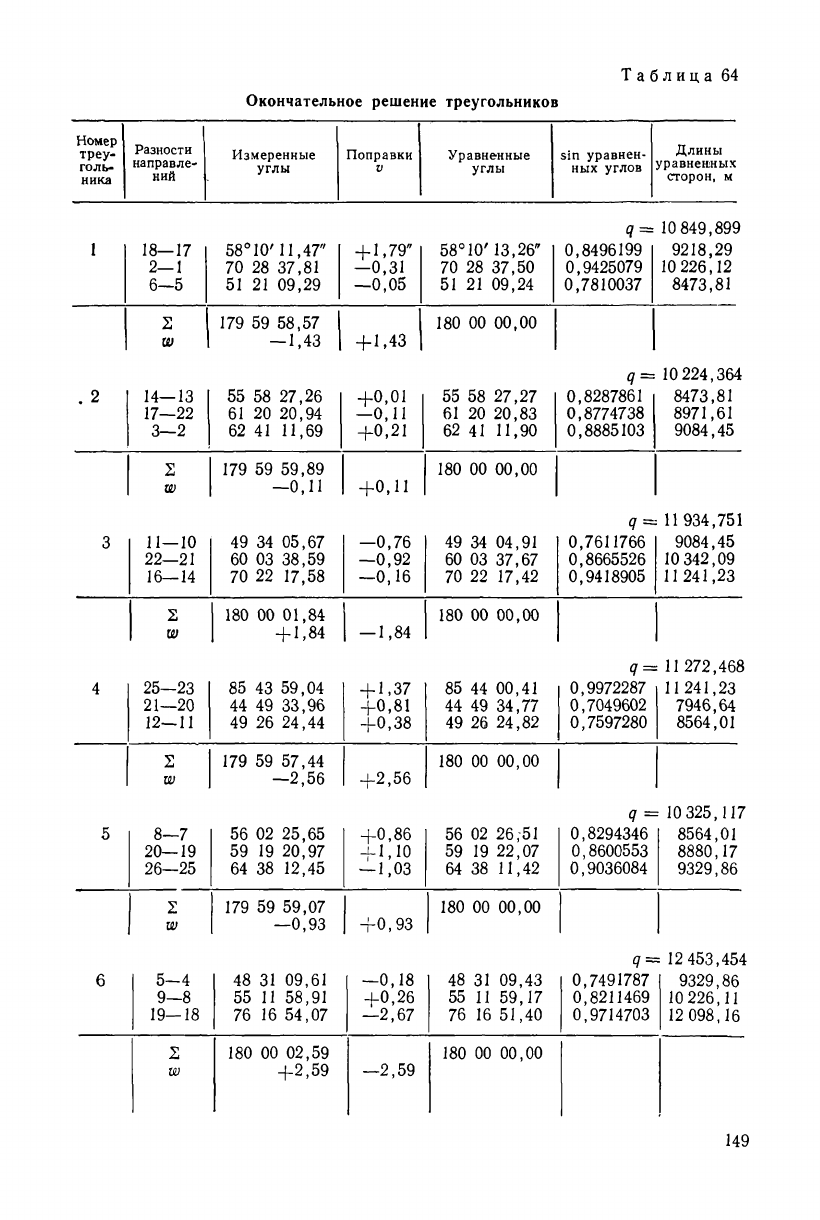
Таблица 78'

Окончательное решение треугольников

Номер

треу-

голь-

ника

Разности

направле-

ний

Измеренные

углы

Поправки

Уравненные

углы

sin уравнен-

ных углов

Длины

уравненных

сторон, м

10 849,899

18-17

2-1

6-5

58°10'11,47"

70 28 37,81

51 21 09,29

+ 1,79"

—0,31

—0,05

58°10'13,26"

70 28 37,50

51 21 09,24

0,8496199

0,9425079

0,7810037

9218,29

10 226,12

8473,81

179 59 58,57 1

— 1,43 1

+ 1,43

180 00 00,00

10 224,364

. 2 14—13

17—22

3—2

55 58 27,26

61 20 20,94

62 41 11,69

+0,01

—0,11

+0,21

55 58 27,27

61 20 20,83

62 41 11,90

0,8287861

0,8774738

0,8885103

8473,81

8971,61

9084,45

179 59 59,89

—0,11

+0,11

180 00 00,00

: 11 934,751

11—10

22—21

16—14

49 34 05,67

60 03 38,59

70 22 17,58

-0,76

—0,92

—0,16

49 34 04,91

60 03 37,67

70 22 17,42

0,7611766

0,8665526

0,9418905

9084,45

10 342,09

11241,23

180 00 01,84

+ 1,84 -1,84

180 00 00,00

: 11 272,468

4 25—23

21—20

12—11

85 43 59,04

44 49 33,96

49 26 24,44

+ 1,37

+0,81

+0,38

85 44 00,41

44 49 34,77

49 26 24,82

0,9972287

0,7049602

0,7597280

11 241,23

7946,64

8564,01

179 59 57,44

—2,56

+2,56

180 00 00,00

10 325,117

8—7

20—19

26—25

56 02 25,65

59 19 20,97

64 38 12,45

+0,86

+ 1,10

— 1,03

56 02 26,51

59 19 22,07

64 38 11,42

0,8294346

0,8600553

0,9036084

8564,01

8880,17

9329,86

179 59 59,07

—0,93 +0,93

180 00 00,00

= 12 453,454

5-4

9-8

19-18

48 31 09,61

55 11 58,91

76 16 54,07

—0,18

+0,26

—2,67

48 31 09,43

55 И 59,17

76 16 51,40

0,7491787

0,8211469

0,9714703

9329,86

10 226,11

12 098,16

180 00 02,59

+2,59

—2,59

180 00 00,00

-149

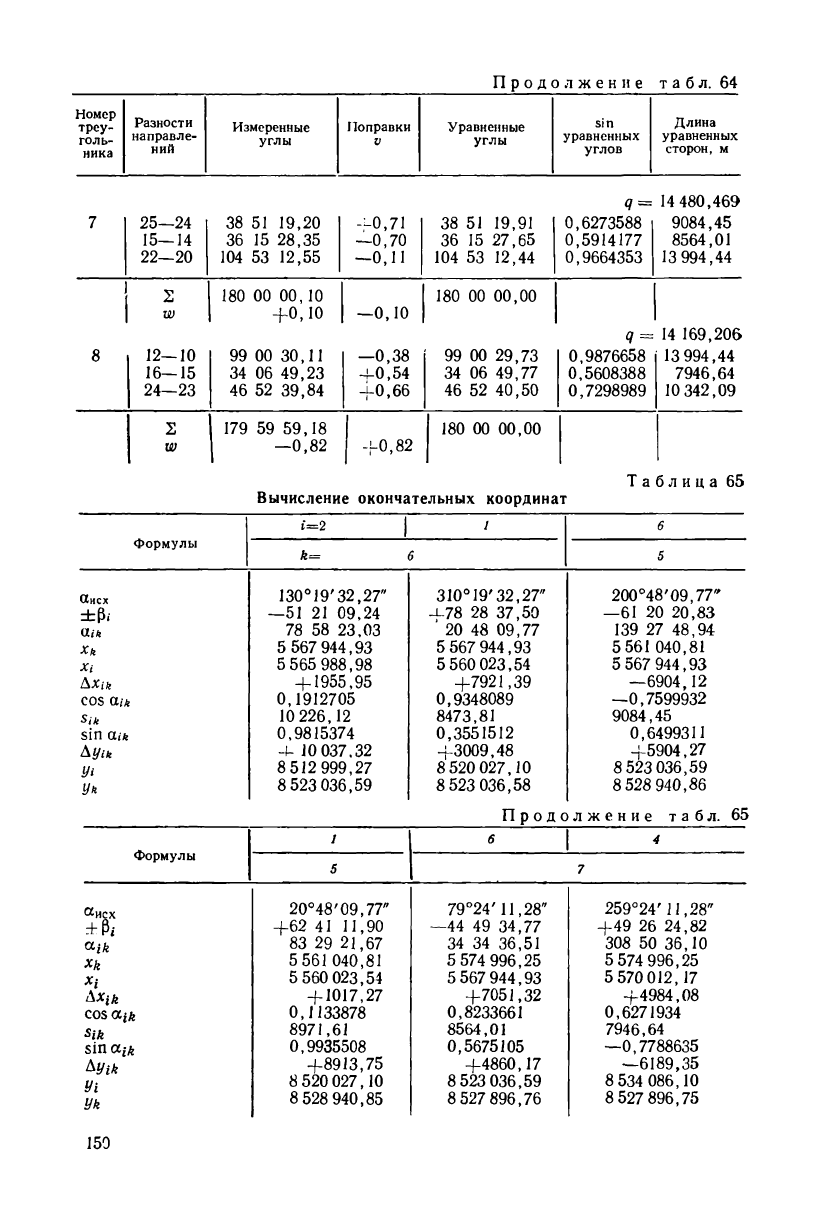
Продолжение табл. 64

Номер

треу-

голь-

ника

Разности

направле-

ний

Измеренные

углы

Поправки

Уравненные

углы

sin

уравненных

углов

Длина

уравненных

сторон, м

<7= 14 480,469

25—24

38 51 19,20

+0,71

38 51 19,91 0,6273588 9084,45

15—14 36 15 28,35

—0,70

36 15 27,65

0,5914177

8564,01

22—20

104 53 12,55

—0,11

104 53 12,44 0,9664353

13 994,44

J V

180 00 00,10

180 00 00,00

1 W

+0,10 —0,10

14 169,206

12—10

99 00 30,11 —0,38

99 00 29,73

0,9876658

13 994,44

16—15 34 06 49,23 -1-0,54

34 06 49,77

0,5608388

7946,64

24—23

46 52 39,84

+0,66

46 52 40,50

0,7298989

10 342,09

2 179 59 59,18

180 00 00,00

—0,82 +0,82

Таблица 65

Вычисление окончательных координат

Формулы

k= i

Оисх

130°19'32,27"

310°19'32,27"

200°48'09,77"

—51 21 09,24

-J-78 28 37,50

—61 20 20,83

a ik

78 58 23,03

' 20 48 09,77

139 27 48,94

5 567 944,93 5 567 944,93

5 561 040,81

5 565 988,98 5 560 023,54

5 567 944,93

&Xik

+ 1955,95

+7921,39

—6904,12

cos а/л

0,1912705

0,9348089

—0,7599932

Sitt

10 226,12

8473,81

9084,45

sin a ik

0,9815374

0,3551512

0,6499311

A y

4- 10 037,32

+3009,48

+5904,27

У1

8 512 999,27

8 520 027,10

8 523 036,59

Ук

8 523 036,59

8 523 036,58

8 528 940,86

Продолжение табл. 65

Формулы

1 6

Формулы

5 7

"исх

cos a ik

Sik

sin a^

tyik

У1

20° AS'№ ,77"

+62 41 11,90

83 29 21,67

5 561 040,81

5 560 023,54

+ 1017,27

0,1133878

8971,61

0,9935508

+8913,75

8 520 027,10

8 528 940,85

79°24'11,28"

-44 49 34,77

34 34 36,51

5 574 996,25

5 567 944,93

+7051,32

0,8233661

8564,01

0,5675105

+4860,17

8 523 036,59

8 527 896,76

259° 24 41,28"

+49 26 24,82

308 50 36,10

5 574 996,25

5 570 012,17

+4984,08

0,6271934

7946,64

--0,7788635

—6189,35

8 534 086,10

8 527 896,75

150

Используя уравненные углы и длины сторон треугольников,

вычислим в табл. 65 окончательные координаты всех определяе-

мых пунктов. В целях дополнительного контроля вычислим коор-

динаты исходного пункта 4. Вычисленные и заданные значения ко-

ординат этого пункта должны совпасть между собой, в противном

случае необходимо найти и исправить ошибки, допущенные при

составлении и решении координатных условных уравнений.

Вычислим сначала среднюю квадратическую ошибку единицы

веса. В нашей сети = 6,64; число избыточных измерений рав-

но числу независимых условных уравнений и равно 13 (г = 13).

С этими данными по формуле (8.25) получим

Среднюю квадратическую ошибку уравненной стороны 5—7

найдем по формуле (8.24), взяв величину обратного веса

= 0,149 из табл. 62 и приняв ц = 0,71". В итоге получим

8&ч

= ц Y~\jP

= 0,71 /07149 = 0,27 дм = 0,03 м.

Средняя квадратическая ошибка уравненного дирекционного

угла этой стороны равна

mcc

= УТ/К = 0,71 /07бИ = 0,56",

где обратный вес 1/Р

=0,614 взят из табл. 62.

§ 46. Последовательность вычислений

при параметрическом способе уравнивания триангуляции

При уравнивании триангуляции параметрическим способом не-

известные поправки измеренных величин представляются в виде

линейных функций, в которых аргументами являются: 1) поправ-

ки | и т] к приближенным координатам определяемых пунктов;

2) поправки ориентирования bz на станциях и 3) свободные чле-

ны I. Другими словами, поправка v в каждое измеренное направ-

ление представляется в виде параметрического уравнения связи

Оценка точности уравненных элементов сети

Средняя квадратическая ошибка уравненного угла

= ji У2 = 1,00".

Глава 10

УРАВНИВАНИЕ ТРИАНГУЛЯЦИИ

ПАРАМЕТРИЧЕСКИМ СПОСОБОМ

Vik^yibZi, r\

и, щ, hk)>

(10.1)

151

Число уравнений поправок (ЮЛ) равно числу измеренных на-

правлений в сети; оно всегда больше числа искомых поправок при-

ближенных координат и поправок ориентирования на станциях.

Подчинив поправки направлений условию [pv

]= min, получим од-

нозначные значения поправок координат и поправок ориентиро-

вания.

Уравнивание триангуляции параметрическим способом вклю-

чает:

1) вычисление приближенных координат^определяемых пунк-

тов;

2) вычисление дирекционных углов всех сторон сети из реше-

ния обратных геодезических задач;

3) составление уравнений поправок для всех измеренных на-

правлений;

4) составление и решение нормальных уравнений;

5) вычисление окончательных значений координат пунктов пу-

тем введения в их приближенные значения поправок, полученных

из решения нормальных уравнений;

6) вычисление поправок ориентирования на станциях и попра-

вок измеренных направлений; окончательное решение треугольни-

ков;

7) вычисление уравненных дирекционных углов, приращений

координат и вторичное определение окончательных координат оп-

ределяемых пунктов (через их приращения);

8) оценка точности уравненных элементов сети. Составление

каталога координат.

Последовательность уравнительных вычислений при использо-

вании параметрического способа рассмотрим на примере уравни-

вания небольшой сети триангуляции.

§ 47. Решение треугольников.

Вычисление приближенных координат и дирекционных углов

Исходная для нашей сети (рис. 45) информация: координаты

исходных пунктов, а также приведенные к центрам знаков и ре-

дуцированные на плоскость измеренные направления даны в

табл. 66.

Для обеспечения необходимой точности вычисления поправок

измеренных направлений требуется, чтобы свободные члены урав-

нений поправок были как можно меньше по величине. Это возмож-

но при условии, если приближенные координаты определяемых

пунктов будут незначительно отличаться от их уравненных значе-

ний. Отсюда вытекает задача получения предварительных коорди-

нат пунктов с возможно большей точностью. С этой целью в боль-

ших сетях выполняют даже приближенное уравнивание измерен-

ных величин.

Прежде чем приступить к решению треугольников и вычисле-

нию координат пунктов, необходимо определить длины и дирекци-

152

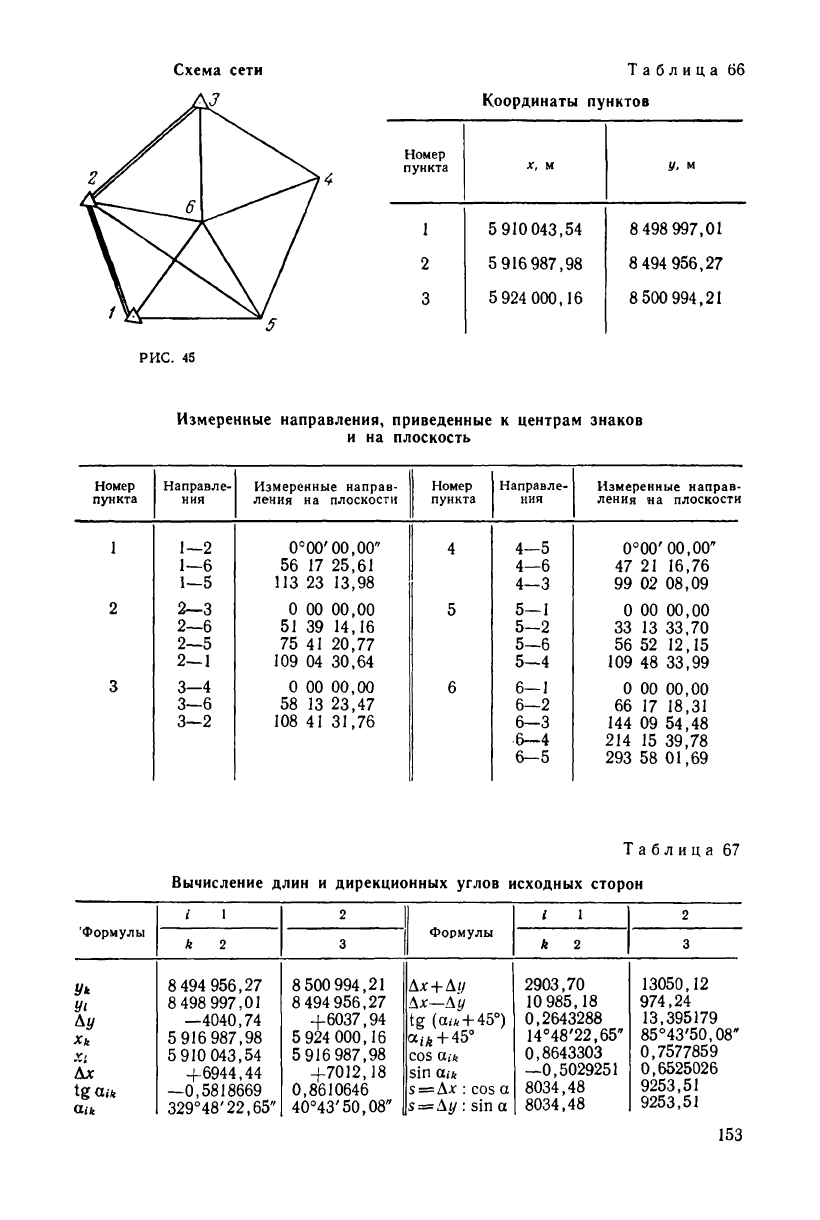
Измеренные направления, приведенные к центрам знаков

и на плоскость

Номер

пункта

Направле-

ния

Измеренные направ-

ления на плоскости

Номер

пункта

Направле-

ния

Измеренные направ-

ления на плоскости

1 1—2

1—6

1-5

0°00' 00,00"

56 17 25,61

ИЗ 23 13,98

4-5

4-6

4-3

0°00' 00,00"

47 21 16,76

99 02 08,09

2-3

2-6

2-5

2-1

0 00 00,00

51 39 14,16

75 41 20,77

109 04 30,64

5—1

5-2

5-6

5-4

0 00 00,00

33 13 33,70

56 52 12,15

109 48 33,99

3-4

3—6

3-2

0 00 00,00

58 13 23,47

108 41 31,76

6 6—1

6—2

6—3

6—4

6-5

0 00 00,00

66 17 18,31

144 09 54,48

214 15 39,78

293 58 01,69

Таблица 67

Вычисление длин и дирекционных углов исходных сторон

'Формулы

< 1

Формулы

i l

'Формулы

k 2 3

Формулы

k 2

Ук

У1

ьу

Кх

tg a ik

CLik

8 494 956,27

8 498 997,01

—4040,74

5 916 987,98

5 910 043,54

+6944,44

—0,5818669

329°48'22,65"

8 500 994,21

8 494 956,27

+6037,94

5 924 000,16

5 916 987,98

+7012,18

0,8610646

40°43'50,08"

Дх + Д//

Ах—А у

tg (ш* + 45°)

«И+ 45°

cos а ik

sin а ik

s = Ал:: cos а

s = A*/: sin а

2903,70

10 985,18

0,2643288

14°48'22,65"

0,8643303

—0,5029251

8034,48

13050,12

974,24

13,395179

85°43'50,08"

0,7577859

0,6525026

9253,51

153

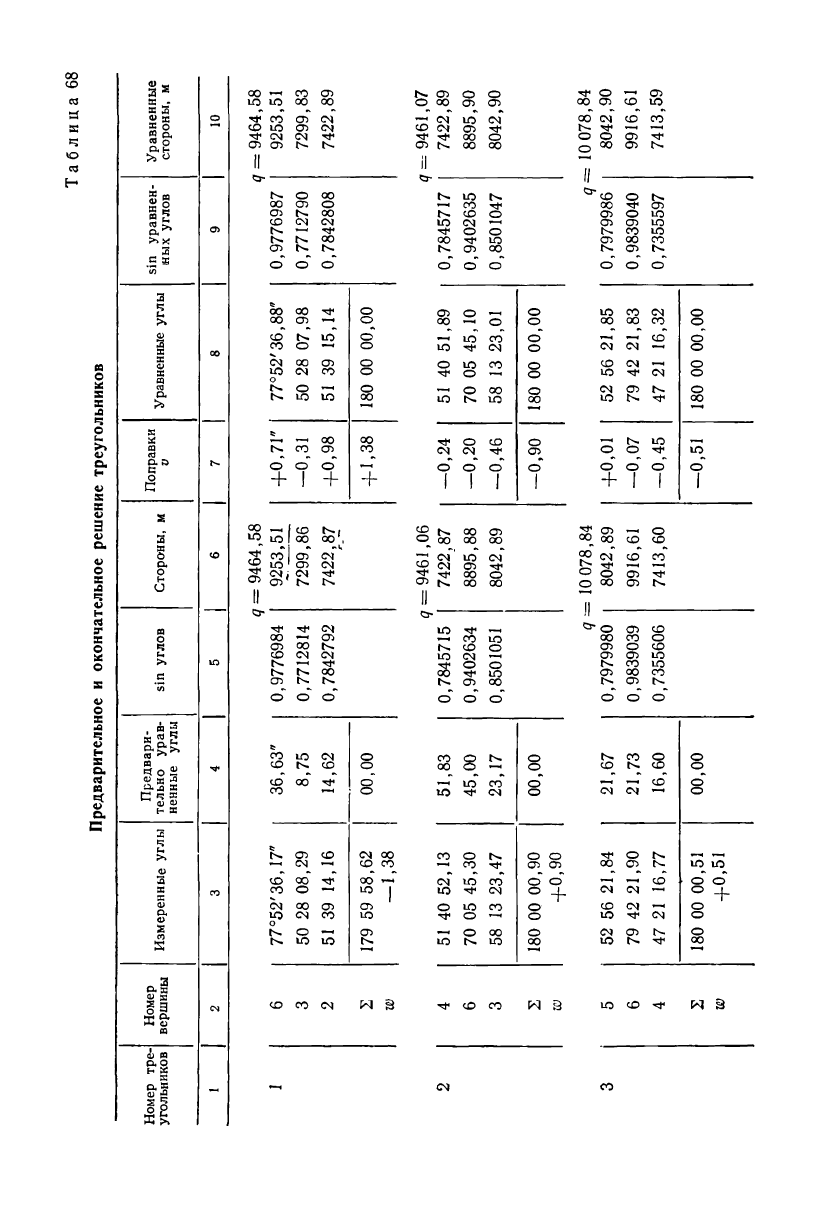
Таблица 79'

Предварительное и окончательное решение треугольников

Номер тре-

угольников

Номер

вершины

Измеренные углы

Предвари-

тельно урав-

ненные углы

sin углов

Стороны, м

Поправки

Уравненные углы

sin уравнен-

ных углов

Уравненные

стороны, м

1 • 1 1 г

9 10

77°52'36,17" 36,63"

0,9776984

= 9464,58

9253,51

+0,71" 77°52'36,88" 0,9776987

= 9464,58

9253,51

50 28 08,29

8,75

0,7712814

7299,86

—0,31 50 28 07,98 0,7712790

7299,83

51 39 14,16

14,62

0,7842792

7422,87

+0,98 51 39 15,14 0,7842808

7422,89

179 59 58,62

— 1,38

00,00 + 1,38 180 00 00,00

2 4

51 40 52,13

51,83

0,7845715

= 9461,06

7422,87

—0,24 5140 51,89

0,7845717

= 9461,07

7422,89

70 05 45,30

45,00

0,9402634

8895,88

—0,20

70 05 45,10 0,9402635

8895,90

58 13 23,47

23,17 0,8501051

8042,89

—0,46 58 13 23,01

0,8501047

8042,90

180 00 00,90

+0,90

00,00

—0,90

180 00 00,00

52 56 21,84

21,67

Я =

0,7979980

= 10 078,84

8042,89 +0,01

52 56 21,85

0,7979986

= 10 078,84

8042,90

79 42 21,90

21,73

0,9839039

9916,61 —0,07 79 42 21,83

0,9839040

9916,61

47 21 16,77

16,60

0,7355606

7413,60

—0,45 47 21 16,32

0,7355597

7413,59

180 00 00,51

+0,51

00,00 -0,51

180 00 00,00

57°05'48,37"

66 01 58,31

56 52 12,15

48,76"

58,70

12,54

0,8395903

0,9137794

0,8374341

r= 8830,02

7413,60

8068,69

7394,56

+0,39"

+0,70

+0,08

57°05'48,76"

66 01 59,01

56 52 12,23

0,8395903

0,9137800

0,8374333

= 8830,01

7413,59

8068,69

7394,54

179 59 58,83

— 1,17

57 25 16,48

66 17 18,31

56 17 25,61

00,00

16,35

18.18

25,47

0,8426518

0,9155811

0,8318612

= 8775,31

7394,56

8034,51

7299,84

+ 1,17

+0,95

-1,14

—0,21

180 00 00,00

57 25 17,43

66 17 17,17

56 17 25,40

0,8426546

0,9155791

0,8318610

f = 8775,29

7394,54

8034,48

7299,82

180 00 00,40

+0,40

33 13 33,70

33 23 09,87

113 23 13,98

00,00

34,52

10,69

14,79

0,5479466

0,5502811

0,9178417

= 14 662,94

8034,51

8068,74

13 458,26

+0,40

+ 1,28

+0,99

+0,18

180 00 00,00

33 13 34,98

33 23 10,86

113 23 14,16

0,5479485

0,5502818

0,9178429

= 14 662,84

8034,48

8068,69

13 458,18

179 59 57,55

—2,45 '

132°19'16,62"

24 02 06,61

23 38 38,45

00,00

16,06"

6,05

37,89

<7 =

0,7393828

0,4072948

0,4010504

= 18 202,02

13 458,26

7413,59

7299,93

+2,45

—0,44"

—0,04

— 1,20

180 00 00,00

132°19'16,18"

24 02 06,57

23 38 37,25

Ч--

0,7393825

0,4072971

0,4010475

= 18 201,92

13 458,18

7413,59

7299,83

180 00 01,68

+ 1,68

00,00

— 1,68

180 00 00,00

= 13,33

« 1 /

2Ш2

-V 3n -

v т

= 0,80"

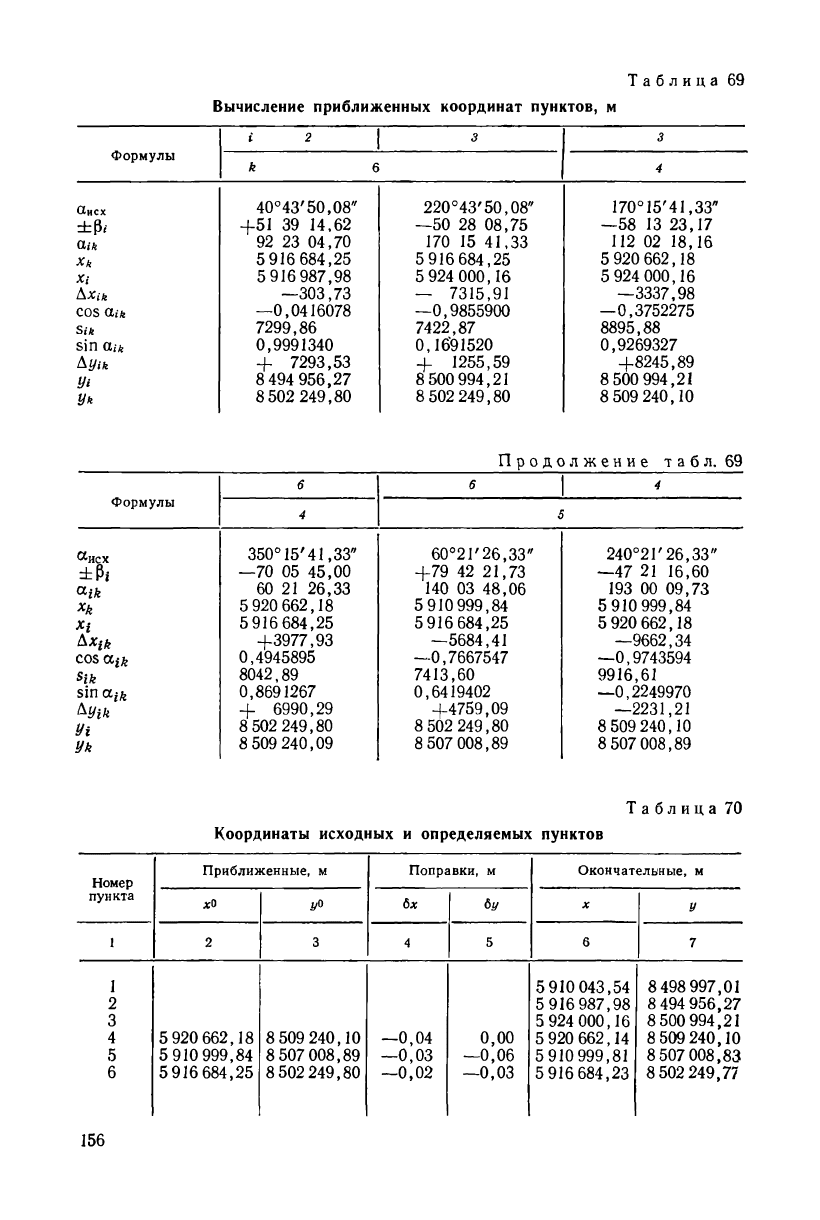
Таблица 78'

Вычисление приближенных координат пунктов, м

Формулы

i 2 |

Формулы

k 6

ССисх

40°43'50,08"

220°43'50,08"

170°15'41,33*

±Р/

+51 39 14,62

—50 28 08,75

—58 13 23,17

a ik

92 23 04,70 170 15 41,33 112 02 18,16

5 916 684,25

5916684,25

5 920 662,18

5 916 987,98

5 924 000,16 5 924 000,16

A x

—303,73

— 7315,91 —3337,98

cos a ik

—0,0416078 —0,9855900

—0,3752275

Sik

7299,86 7422,87 8895,88

sin a ik

0,9991340

0,1691520

0,9269327

A y

+ 7293,53

+ 1255,59 +8245,89

У1

8 494 956,27

8 500 994,21

Ук

8 502 249,80

8 509 240,10

Продолжение табл. 69

Формулы

4 5

&ИСХ

350°15'41,33" 60°21'26,33"

240°2Г26,33"

—70 05 45,00

+79 42 21,73

—47 21 16,60

ttik

60 21 26,33 140 03 48,06

193 00 09,73

5 920 662,18

5 910 999,84 5 910 999,84

5 916 684,25 5 916 684,25

5 920 662,18

+3977,93 —5684,41

—9662,34

cos aik

0,4945895

—0,7667547

—0,9743594

Sik

8042,89

7413,60

9916,61

sin a ik 0,8691267

0,6419402

—0,2249970

A yik

+ 6990,29 +4759,09

—2231,21

Уг

8 502 249,80

8 509 240,10

Ук

8 509 240,09 8 507 008,89

8 507 008,89

Таблица 70

Координаты исходных и определяемых пунктов

Номер

пункта

Приближенные, м

Поправки, м

Окончательные, м

Номер

пункта

*о

У*

бх

бу

1 2

5 6

5 920 662,18

5 910 999,84

5 916 684,25

8 509 240,10

8 507 008,89

8 502 249,80

—0,04

—0,03

—0,02

0,00

—0,06

—0,03

5 910 043,54

5 916 987,98

5 924 000,16

5 920 662,14

5910999,81

5 916 684,23

8 498 997,01

8 494 956,27

8 500 994,21

8 509 240,10

8 507 008,83

8 502 249,77

-156

онные углы исходных сторон из решения обратных геодезических

задач (табл. 67) по формулам

Ук

—

Уг

Ьу

ща/Л- xk — xi — Ах '

Ах + Ay

tg («ift + 45°) = "д^Здр".

«/Л

cos a

sin <Xik

= /Ax

+ A(/

(10.2)

(10.3)

Таблица 71

Вычисление дирекционных углов всех сторон сети по координатам

Формулы

6 4

6 5

Ук

У1

А У

Ах

Шк

dik

Контроль:

Ах + Ау

Ах—Ау

tg (a

+ 45°)

+45°

sin a ik

cos a ik.

s = Ay

sin a

s=Ax : cos a

8 502 249,80

8 494 956,27

4-7293,53

5 916 684,25

5 916 987,98

—303,73

—24,013158

92°23' 04,70"

6989,80

—7597,26

—

0,9200421

137°23'04,70"

0,9991328

—0,0416076

7299,86

8 509 240,10

8 500 994,21

+8245,89

5 920 662,18

5 924 000,16

—3337,98

—2,4703216

112°02'18,16"

4907,91

—

583,87

—0,4236845

J57°02'18,16"

0,9269335

—0,3752276

8895,88

8 502 249,80

8 500 994,21

+ 1255,59

5 916 684,25

5 924 000,16

—7315,91

—0,1716252

170°15'41,33"

—6060,32

—8071,50

0,7070306

215°15'41,33"

0,1691515

—0,9855904

7422,87

8 507 008,89

8 498 997,01

+ 8011,88

6 910 999,84

5 910 043,54

+ 956,30

8,3779985

83°11'36,1Г

8968,18

—7055,58

—1,2710762

128°11'36,1Г

0,9929518

0,1185190

8068,75

Продолжение табл. 71

Формулы

4 4

Формулы

Ук

У1

А У

tg Щк

Щк

Контроль:

Ax +А у

Ax — Ay

tg(a«* + 45°:

ai*+45°

sina^

cosa^

s = Ay:sina

s = Ax:cosa

8 502 249,80

8 498 997,01

+3252,79

5 916 684,25

5910043,54

+6640,71

0,4898256

26°05'48,47"

9893,50

3 387,92

2,9202283

71°05'48,47"

0,4398890

0,8980522

7394,57

8 507 008,89

8 494 956,27

+ 12 052,62

5 910 999,84

5 916 987,98

—5988,14

—2,0127484

116°25'10,94"

6064,48

— 18 040,76

-0,3361543

161°25'10,94"

0,8955589

—0,4449432

13458,21

8 507 008,89

8 509 240,10

— 2231,21

5 910 999,84

5 920 662,18

— 9662,34

0,2309179

193°00'09,73"

—

893,55

—7431,13

1,6005025

238°00'09,73"

—0,2249972

—0,9743591

9916,61

8 502 249,80

8 509 240,10

— 6990,30

5 916 684,25

5 920 662,18

— 3977,93

1,7572688

240°2Г26,33"

—10 968,23

3012,37

—3,6410700

285°21'26,33"

—0,8691278

—0,4945896

8042,89

8 502 249,80

8 507 008,89

—4759,09

5 916 684,25

5910999,84

+5684,41

—0,8372172

320°03'48,07"

925,32

10443,50

0,0886029

5°03'48,07"

—0,6419404

0,7667543

7413,60

157

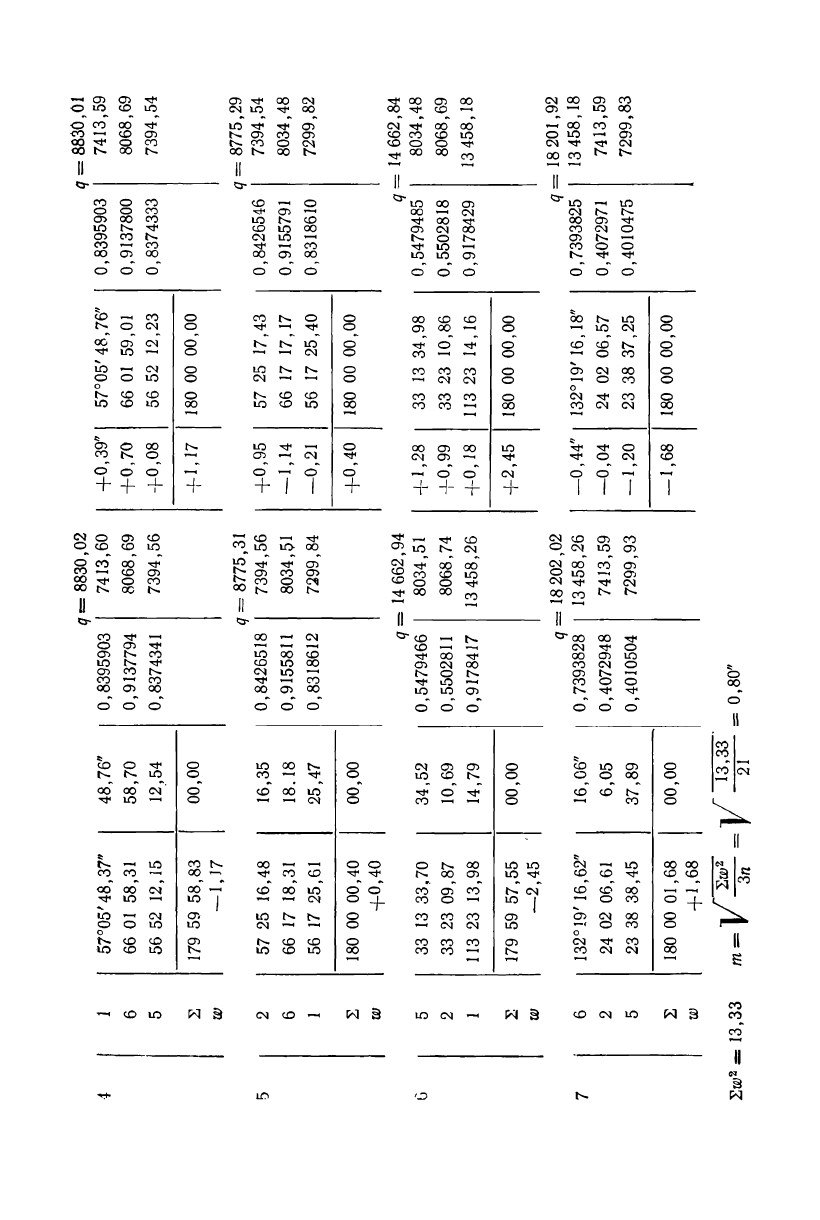
Получив длины и дирекционные углы исходных сторон, присту-

пают к решению треугольников. Невязки w в каждом треугольни-

ке распределяют поровну на все три угла так, чтобы сумма углов

была равна 180°. Это позволит контролировать вычисления коор-

динат. Результаты решения треугольников приведены в табл. 68;

графы 7—10 заполняют после решения нормальных уравнений и

вычисления поправок направлений.

Приближенные координаты каждого вновь определяемого пунк-

та вычисляют в табл. 69 по двум сторонам треугольника с точ-

ностью до сантиметра. Среднее арифметическое из двух значений

координат пункта выписывают в табл. 70, в которую вносят так-

же координаты исходных пунктов.

В табл. 70 графы 4—7 заполняют после решения системы нор-

мальных уравнений, т. е. после вычисления поправок 6*, к при-

ближенным координатам х°, у

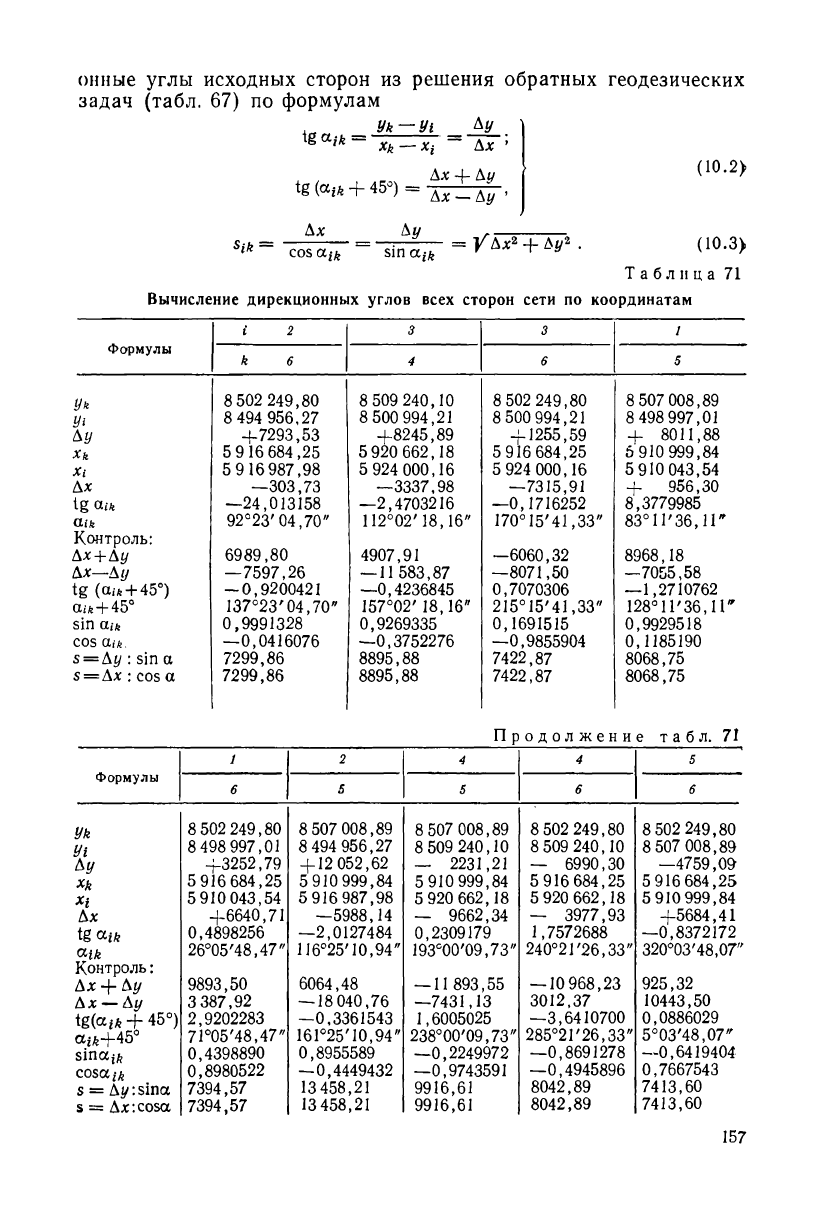
Табл. 70 является исходной для вычисления коэффициентов и

свободных членов уравнений поправок. Используя координаты,

приведенные в табл. 70, вычисляют в табл. 71 по формулам (10.2)

дирекционные углы а всех сторон сети с возможно большей точ-

ностью (до 0,01" в триангуляции 2 класса). Результаты вычисле-

ний ia контролируют по формулам (10.3).

Обратные геодезические задачи необходимо решить по всем

сторонам сети, так как дирекционные углы должны точно соответ-

ствовать координатам, записанным в табл. 70. В противном слу-

чае, когда такое соответствие окажется нарушенным, свободные

члены уравнений поправок будут вычислены неточно, а это неиз-

бежно приведет к необходимости переуравнивания сети, так как

из-за погрешностей в свободных членах уравнений поправок цель

уравнивания достигнута не будет.

Для направления, измеренного с определяемого пункта i на оп-

ределяемый пункт k

уравнение поправок записывается в виде

где bzi — поправка ориентирующего угла z°i на станции, г)/,

f\k — поправки -к приближенным координатам Л, y°i и x°k, y°k

соответственно, выраженные в дециметрах:

где поправки дх и Ьу к координатам этих пунктов даны в метрах;

dik и bik — коэффициенты, Uk — свободный член уравнения попра-

вок.

Коэффициенты a

> bik вычисляют по формулам

§ 48. Уравнения поправок направлений

Vik = — Ьц — aikli —b

\\i + a

+ bi

rik+hk>

(10.4)

I = 106х;

т]

= 106*/,

(10.5)

(10.6)

158