Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

Для нашей сети (см. рис. 39) условное уравнение дирекцион-

ных углов (суммы углов) при уравнивании направлений запишет-

ся в виде

(4) - (б) +

ау

= 0,

где w = а'

— а

= а

— (6 — 4) — а

Свободный член условия дирекционных углов вычислен в

табл. 55.

Таблица 55

Формула

Результаты вычислений Формула Результаты вычислений

«21

С = 6—4

130°19'32,27"

99 52 18,90

«'23

—«23

30°27'13,37"

30 27 13,60

„ f

30 27 13,37

—0,23

^доп = 2,5 Vm"

n + 2т*« = 2,5 У 1*.1 + 2-1,1

= 4,62".

Окончательный вид условного уравнения дирекционных углов

(суммы углов):

(4) — (6) — 0,23" — 0.

Составление условных уравнений абсцисс и ординат. Коорди-

натные условия возникают, если в сети имеются избыточные

пункты с заданными координатами, входящие в разные группы,

удаленные одна от другой не менее чем на две определяемые

стороны. Отдельная труппа жестких пунктов может состоять ли-

бо из одного пункта, либо из нескольких смежных пунктов с за-

данными координатами (см .рис. 44).

Для составления условий абсцисс и ординат выделяют в сети

цепочку треугольников, соединяющую ближайшие пункты разных

групп исходных пунктов, и в ней намечают ходовую линию для пе-

редачи координат, проходящую через вершины промежуточных уг-

лов. При соблюдении указанного правила выбора ходовой линии

условные уравнения координат запишутся в виде:

условное уравнение абсцисс (при уравнивании углов)

2 (х

- *)

км

ctg Л' (Л) - 2 (х

- х)

1Ш

ctg В' (В) -

~ 2 (у

~У)ки (±С) + 206,265^ = 0; (9.18)

условное уравнение ординат (при уравнивании углов)

(Уп

У)км

ctg Л' (Л) — 2 (у

- у)км ctg В' (В) +

+ 2 (х

- *)км (±С) + 206,265», = 0, (9.19)

где w

= x

'— х

; w

' —у

- (9.20)

В выражениях (9.18) — (9.20) х

, у

\ х, (/ — соответственно ко-

ординаты последнего (п) и текущих пунктов ходовой линии, про-

ходящей через вершины промежуточных углов; (Л), (В)—по-

правки связующих углов А и В, причем угол В лежит против ис-

139

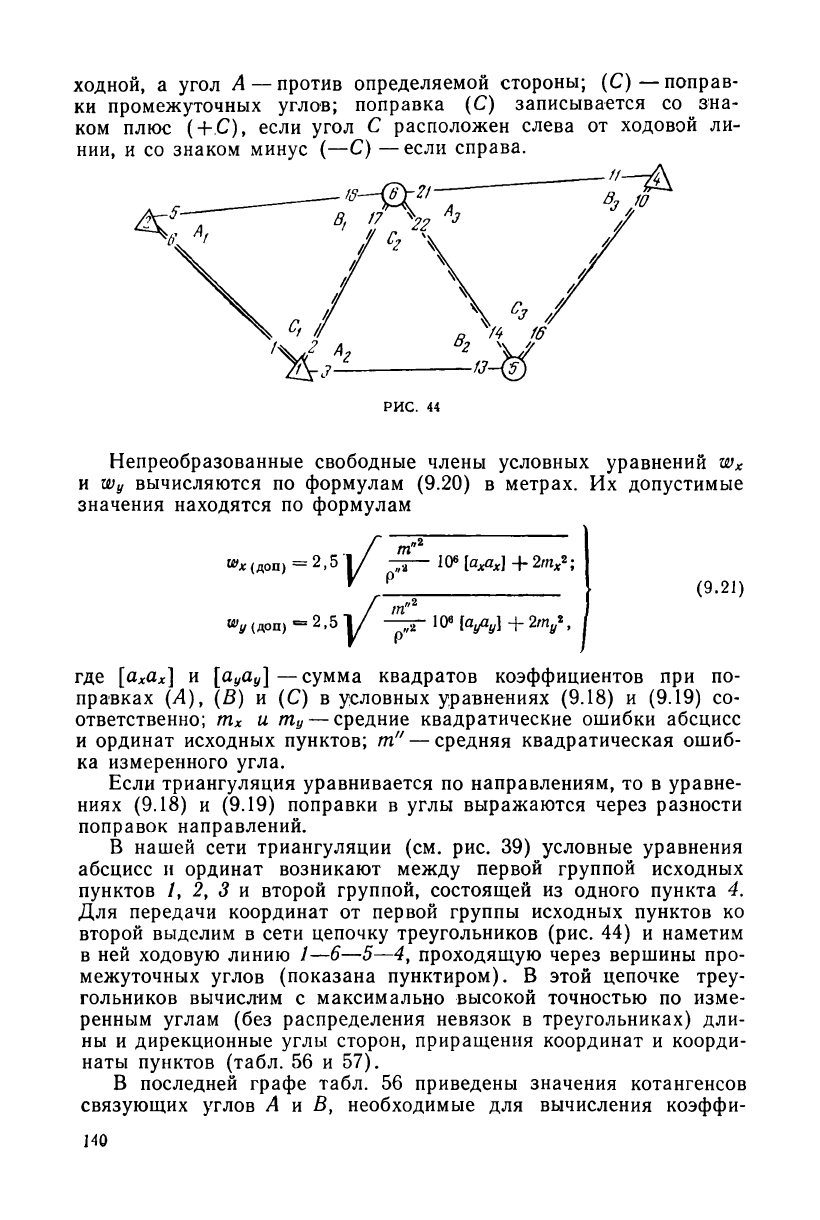
ходной, а угол Л —против определяемой стороны; (С)—поправ-

ки промежуточных углов; поправка (С) записывается со зна-

ком плюс (+,С), если угол С расположен слева от ходовой ли-

нии, и со знаком минус (—С) —если справа.

РИС. 44

Непреобразованные свободные члены условных уравнений w

и w

вычисляются по формулам (9.20) в метрах. Их допустимые

значения находятся по формулам

10*

[ад,]+2т

„2

(доп) = 2,5 Л/ 10

Iciyciy]

+ 2т

(9.21)

где [а

] и [а

]—сумма квадратов коэффициентов при по-

правках (Л), (В) и (С) в условных уравнениях (9.18) и (9.19) со-

ответственно; т

и т

— средние квадратические ошибки абсцисс

и ординат исходных пунктов; т" — средняя квадратическая ошиб-

ка измеренного угла.

Если триангуляция уравнивается по направлениям, то в уравне-

ниях (9.18) и (9.19) поправки в углы выражаются через разности

поправок направлений.

В нашей сети триангуляции (см. рис. 39) условные уравнения

абсцисс и ординат возникают между первой группой исходных

пунктов /, 2, 3 и второй группой, состоящей из одного пункта 4.

Для передачи координат от первой группы исходных пунктов ко

второй выделим в сети цепочку треугольников (рис. 44) и наметим

в ней ходовую линию 1—6—5—4, проходящую через вершины про-

межуточных углов (показана пунктиром). В этой цепочке треу-

гольников вычислим с максимально высокой точностью по изме-

ренным углам (без распределения невязок в треугольниках) дли-

ны и дирекционные углы сторон, приращения координат и коорди-

наты пунктов (табл. 56 и 57).

В последней графе табл. 56 приведены значения котангенсов

связующих углов Л и В, необходимые для вычисления коэффи-

140

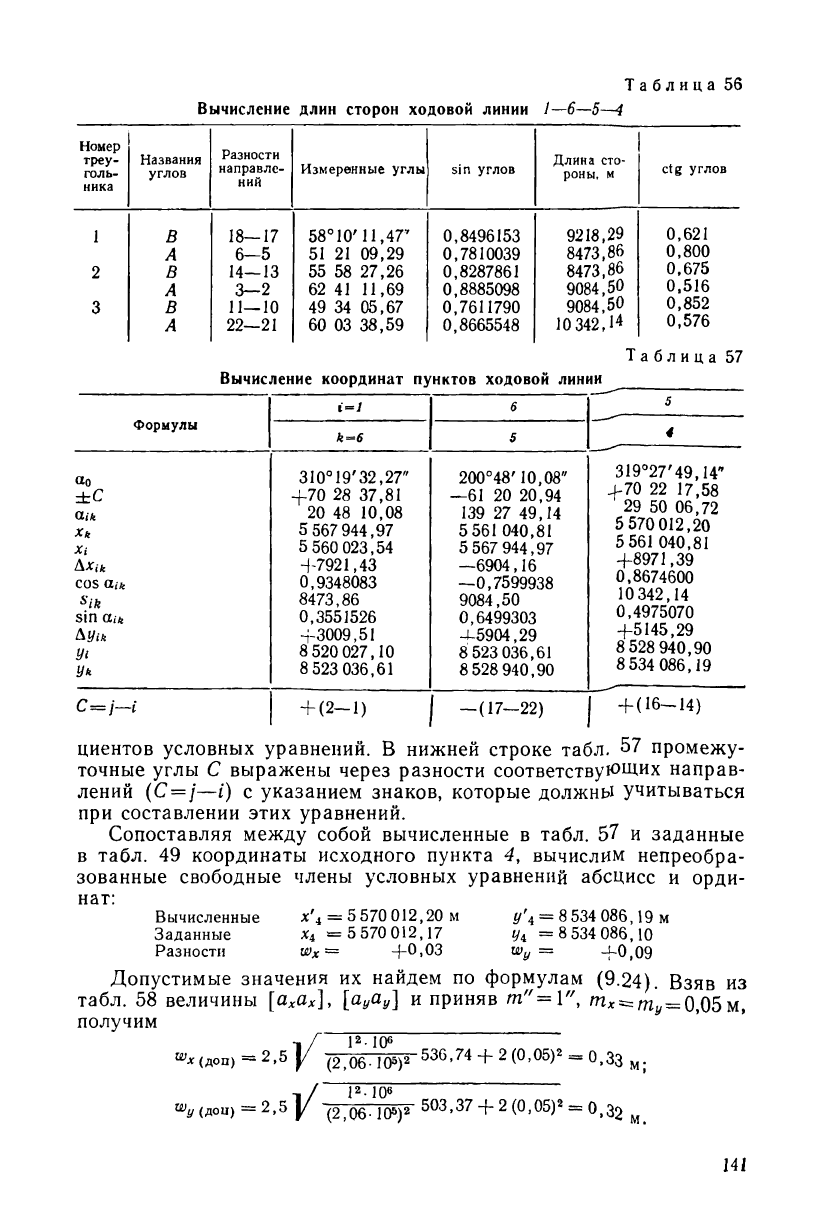
Таблица 78'

Вычисление длин сторон ходовой линии 1—6—5—4

Номер

треу-

голь-

ника

Названия

углов

Разности

направле-

ний

Измеренные углы

sin углов

Длина сто-

роны, м

ctg углов

В 18—17

58°10'11,47*

0,8496153

9218,29

0,621

6-5 51 21 09,29 0,7810039

8473,86

0,800

14-13

55 58 27,26

0,8287861

8473,86 0,675

3—2

62 41 11,69

0,8885098

9084,50 0,516

11—10

49 34 05,67

0,7611790

9084,50

0,852

22—21

60 03 38,59 0,8665548

10 342,14

0,576

Таблица 57

Вычисление координат пунктов ходовой линии

Формулы

i=/

Формулы

310°19'32,27"

200°48'10,08"

±с

+70 28 37,81

—61 20 20,94

а ik

20 48 10,08

139 27 49,14

5 567 944,97

5 561 040,81

5 560 023,54

5 567 944,97

+7921,43

—6904,16

cos

a,ik

0,9348083

—0,7599938

8473,86 9084,50

sin a ik

0,3551526

0,6499303

A yik

+3009,51

4-5904,29

8 520 027,10

8 523 036,61

Ук

8 523 036,61

8 528 940,90

+ (2-1) | —(17—22) |

319°27'49,14"

>70 22 17,58

29 50 06,72

5 570 012,20

5 561 040,81

+8971,39

0,8674600

10 342,14

0,4975070

+5145,29

8 528 940,90

8 534 086,19

+ (16—14)

циентов условных уравнений. В нижней строке табл. 57 промежу-

точные углы С выражены через разности соответствующих направ-

лений (С = /—0 с указанием знаков, которые должны учитываться

при составлении этих уравнений.

Сопоставляя между собой вычисленные в табл. 57 и заданные

в табл. 49 координаты исходного пункта 4, вычислим непреобра-

зованные свободные члены условных уравнений абсцисс и орди-

нат:

Вычисленные х'

= 5 570 012,20 м у'

= 8 534 086,19 м

Заданные х

= 5 570 012,17 у

= 8 534 086,10

Разности w

= +0,03 w

= +0,09

Допустимые значения их найдем по формулам (9.24). Взяв из

табл. 58 величины [а

], [а

] и приняв т"=1",

—

0,05м,

получим

(Д°п)

= 2,5]/'

^(ДОЦ) =2,5]/-

12.J0

(2,06-10

)

2 536

2 (0

05)2 в

°»33

РЛоё

(2,06-10

)

2 503

(°'°

)

= 0,32

м:

м.

-141

Вычисление коэффициентов

Номер

треу-

голь-

ника

Номер

пункта

ходовой

линии

X, км

5560+

у, км

8520+

Ах=х

—х,

км

Ьу=у

—у<

км

ctg

ctg В

Название

Номер

треу-

голь-

ника

Номер

пункта

ходовой

линии

X, км

5560+

у, км

8520+

Ах=х

—х,

км

Ьу=у

—у<

км

ctg

ctg В

И)

2 3

5 6 7 8 | 9

0,023

7,945

1,041

10,012

0,027

3,037

8,941

14,086

9,989

2,067

8,971

0,000

14,059

11,049

5,145

0,000

0,800

0,516

0,576

0,621

0,675

0,852

(6—5)

(3-2)

(22—21)

Свободные члены условных уравнений абсцисс и ординат рав-

ны:

= 206,265k;* = 6,19;

' = 206,265^= 18,56.

За порядком составления условных уравнений абсцисс и орди-

нат проследим по табл. 58. В графах 3 и 4 этой таблицы приведе-

ны координаты пунктов ходовой линии, выраженные в километрах.

В графах 5 и 6 вычислены разности координат последнего и те-

кущего пунктов ходовой линии. В графах 7 и 8 выписаны из

табл. 56 котангенсы связующих углов треугольников. В графах

9—11 записаны номера углов Л, В и С соответственно при поправ-

ках (Л), (В) и (С) координатных условных уравнений; при этом

углы С записаны с теми же знаками, что и в табл. 57. В графах

12—14 вычислены коэффициенты условного уравнения абсцисс

(9.18), а в графах 15—17 — коэффициенты условного уравнения

ординат (9.19), причем в обоих случаях для уравнивания сети по

углам. В нижней строке табл. 58 вычислены суммы квадратов ко-

эффициентов этих уравнений.

Для того чтобы избежать значительных по величине коэффи-

циентов в нормальных уравнениях коррелат, следует коэффициен-

ты условных уравнений сделать близкими к единице. С этой целью

все коэффициенты и свободные члены условных уравнений абс-

цисс и ординат уменьшим в 10 раз. В итоге получим:

условное уравнение абсцисс (при уравнивании углов)

+0,799 (6 — 5) + 0,107 (3 — 2) + 0,517 (22 — 21) —

— 0,620(18 —17) — 0,140(14 — 13) — 0,764 (11 — 10) — 1,406 (2— 1) +

+ 1,105 (17 —22) — 0,515 (16 — 14) + 0,62 = 0;

условное уравнение ординат (при уравнивании углов)

+ 1,125 (6 — 5) + 0,570 (3 — 2) + 0,296 (22 - 21) — 0,873 (18 — 17) —

_ 0,746 (14 — 13) — 0,438 (11 — 10) + 0,999 (2 — 1) _

— 0,207 (17 — 22) + 0,897 (16— 14) + 1,86 = 0.

142

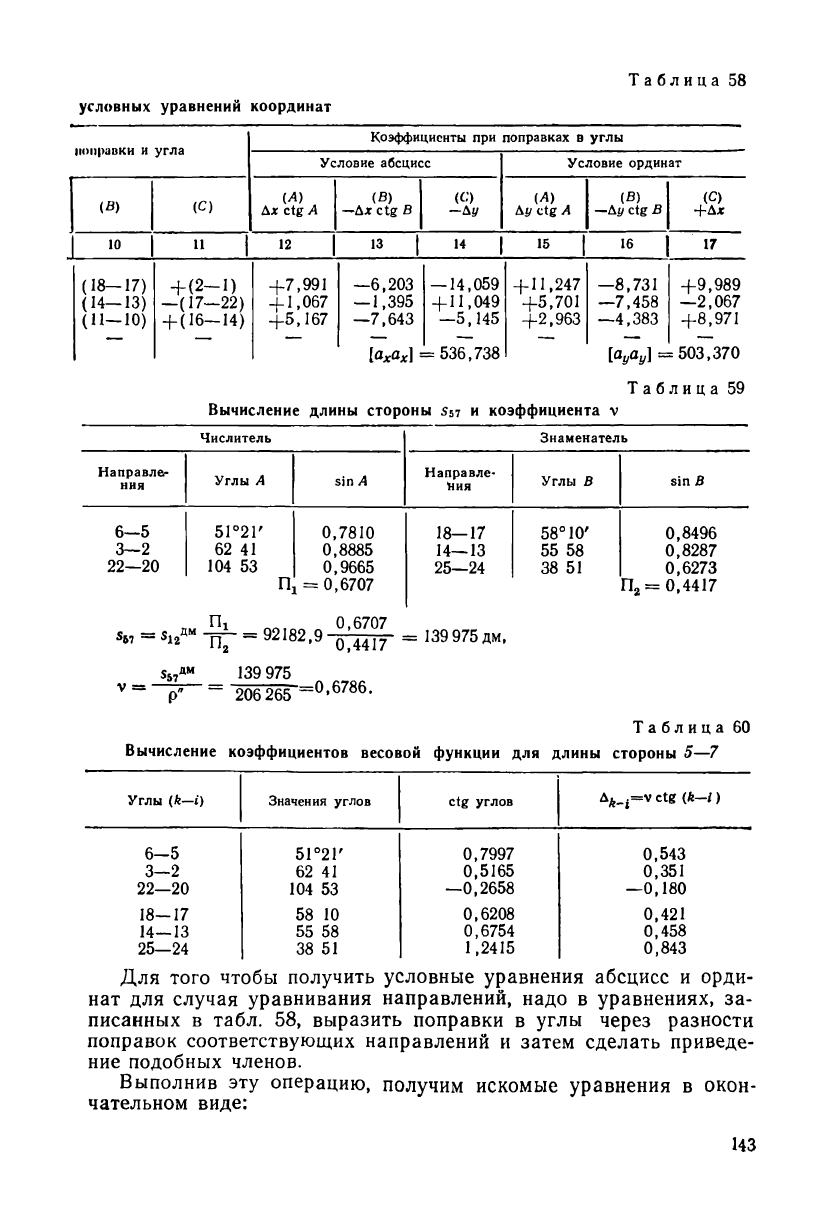
Таблица 78'

условных уравнении координат

поправки и угла

(В)

(С)

Коэффициенты при поправках о углы

Условие абсцисс

Ддг ctg А

(В)

—Ддг ctg В

(С)

-Л у

Условие ординат

(Л)

Ду ctg А

(В)

—Ду ctg В

(С)

13 14 15 16

(18—17)

(14—13)

(11-10)

+ (2-1)

—(17—22)

+ (16—14)

+7,991

+ 1,067

+5,167

-6,203

-1,395

-7,643

— 14,059

+ 11,049

-5,145

+ 11,247

+5,701

+2,963

—8,731

—7,458

—4,383

[а

] = 536,738

Вычисление длины стороны s

7 и коэффициента v

+9,989

—2,067

+8,971

[а

] =503,370

Таблица 59

Числитель

Знаменатель

Направлег

ння

Углы А

sin А

Направле-

ния

Углы В

sin В

6-5

3—2

22—20

5Г2Г

62 41

104 53

0,7810

0,8885

0,9665

18—17

14—13

25—24

58°10'

55 58

38 51

0,8496

0,8287

0,6273

= 0,4417

П, 0,6707

= *1

дм

-ц- » 92182,9

;

4417

= 139 975 дм,

ДМ

139 975

v==

р"

206 265

•

6786

Таблица 60

Вычисление коэффициентов весовой функции для длины стороны 5—7

Углы (k—i)

Значения углов

ctg углов

6-5

3-2

22—20

18-17

14—13

25—24

51°2Г

62 41

104 53

58 10

55 58

38 51

0,7997

0,5165

—0,2658

0,6208

0,6754

1,2415

0,543

0,351

—0,180

0,421

0,458

0,843

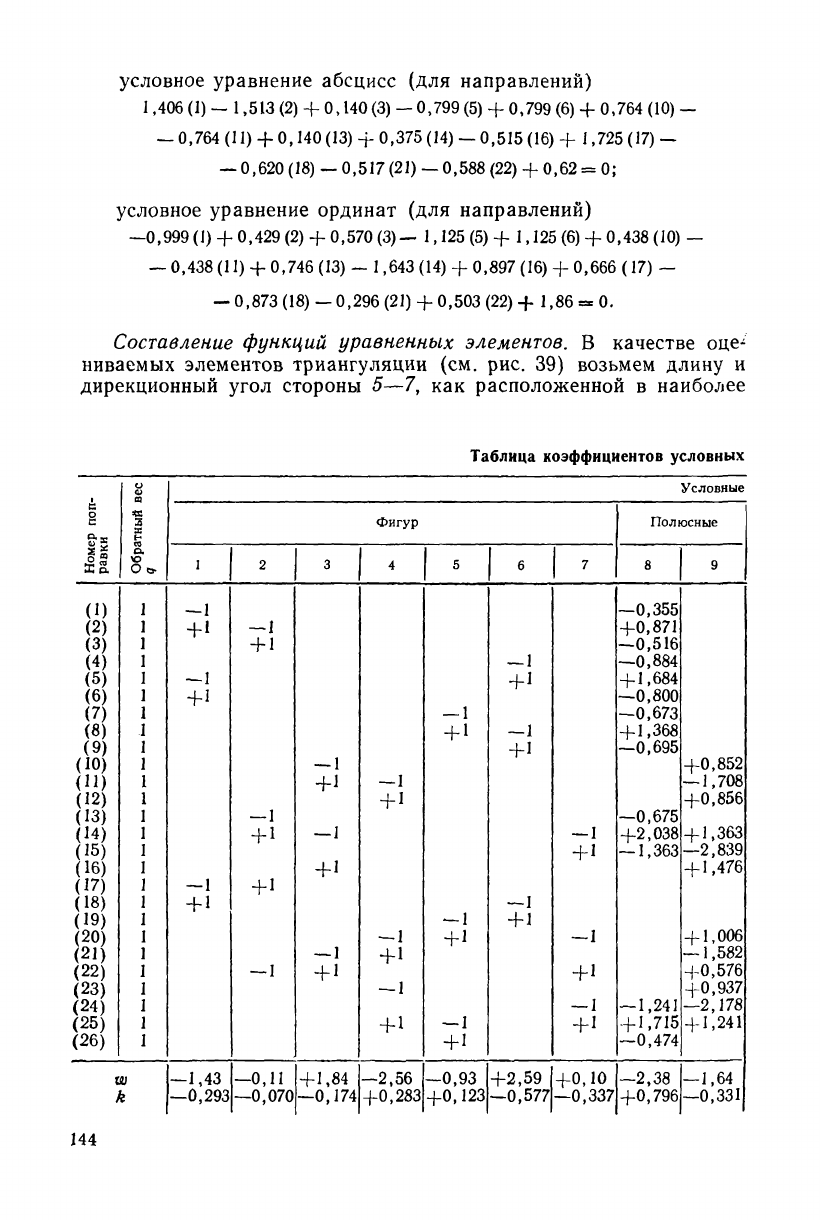
Для того чтобы получить условные уравнения абсцисс и орди-

нат для случая уравнивания направлений, надо в уравнениях, за-

писанных в табл. 58, выразить поправки в углы через разности

поправок соответствующих направлений и затем сделать приведе-

ние подобных членов.

Выполнив эту операцию, получим искомые уравнения в окон-

чательном виде:

-143

условное уравнение абсцисс (для направлений)

1,406 (1) — 1,513 (2) + 0,140(3) — 0,799 (5) + 0,799 (6) + 0,764 (10) —

— 0,764 (11) + 0,140 (13) + 0,375 (14) — 0,515 (16) + 1,725 (17) —

— 0,620 (18) — 0,517 (21) — 0,588 (22) + 0,62 = 0;

условное уравнение ординат (для направлений)

—0,999(1)+ 0,429 (2)+ 0,570(3)— 1,125 (5) + 1,125 (6) + 0,438 (10) —

— 0,438 (11) + 0,746 (13) — 1,643 (14) + 0,897 (16) + 0,666 (17) —

— 0,873 (18) — 0,296 (21) + 0,503 (22) + 1,86 « 0.

Составление функций уравненных элементов. В качестве оце-

ниваемых элементов триангуляции (см. рис. 39) возьмем длину и

дирекционный угол стороны 5—7, как расположенной в наиболее

Таблица коэффициентов условных

<и

Условные

Фигур

Полюсные

°-х

s 3.

о.

>о

О о

I 2

8 9

(1)

— 1

—0,355

(2)

+ 1

— 1

+0,871

(3)

+ 1

—0,516

(4)

— 1

—0,884

(5)

— 1

+ 1

+ 1,684

(6)

+ 1

—0,800

(7)

+ 1

—

—0,673

(8)

—1 + 1,368

(9)

—0,695

(10)

—

+0,852

(И)

— 1

— 1,708

(12) 1

+ 1

+0,856

(13)

1 — 1

+ 1

—0,675

(14) 1

+ 1

— 1 — 1

+2,038

+ 1,363

(15) 1

+ 1

— 1,363

—2,839

(16)

+ 1

+ 1,476

(17)

1 — 1

+ 1

(18) 1

—1

(19) 1

— 1

+ 1

(20)

— 1

+ 1

— 1

+ 1,006

(21)

— 1

+ 1

— 1,582

(22) 1

— 1

+ 1

+0,576

(23) 1

— 1

+ 1

+0,937

(24)

— 1 — 1,241

—2,178

(25) 1

+ 1

— 1

+ 1

+ 1,715 + 1,241

(26)

+ 1

—0,474

w —1,43

—0,11

+1,84

—2,56

—0,93

+2,59

+0,10

—2,38

—1,64

—0,293

—0,070

—0,174

+0,283

+0,123

-0,577

—0,337

+0,796

—0,331

144

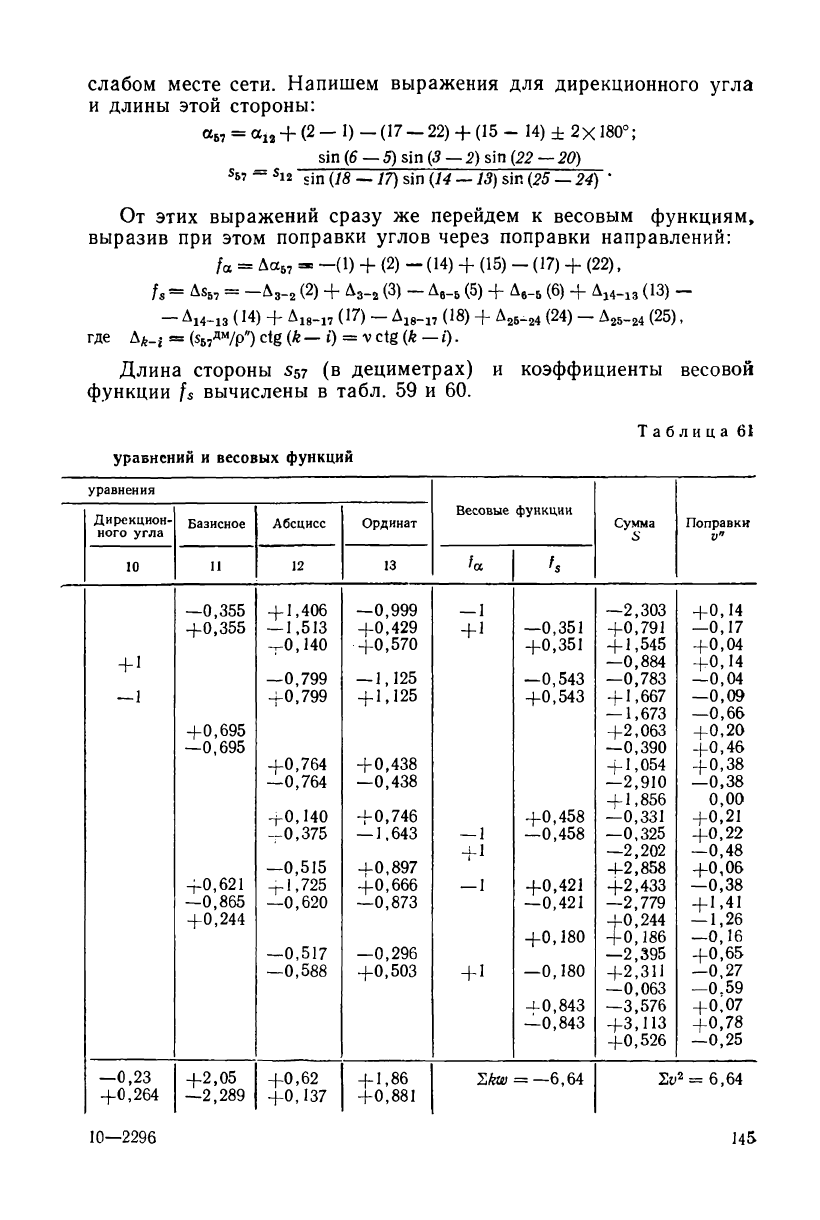
слабом месте сети. Напишем выражения для дирекционного угла

и длины этой стороны:

«67

i2 +

(17

22)

(15

- 14) ± 2Х 180°;

_ sin

(6 — 5)

sin

— 2) sin

(22

—

20)

cin

(18

—

17)

sin

(14

—13) sin

(25

— 24) *

От этих выражений сразу же перейдем к весовым функциям,

выразив при этом поправки углов через поправки направлений:

fa = Дсс

»-(!) + (2) -(14) + (15) - (17) + (22),

- As

= —Д3-2 (2) + А3-2 (3) - Л

(5)

+ Д

(6) + А

а4

(13) -

— ^14-13

(14) + ^18-17 (17)-

(18)

26-24 (24)- (25),

где A

о. (s

/р") ctg

(k —

0 = v ctg (k

—

Длина стороны S57 (в дециметрах) и коэффициенты весовой

функции f

вычислены в табл. 59 и 60.

Таблица 61

уравнений и весовых функций

уравнения

Дирекцион-

ного угла

Базисное

Абсцисс Ординат

Весовые функции

Сумма

Поправки

12 13

1а

+ 1

— 1

—0,355

+0,355

+0,695

—0,695

+0,621

—0,865

+0,244

+ 1,406

-1,513

-рО,140

—0,799

+0,799

+0,764

-0,764

+0,140

--0,375

—0,515

+1,725

—0,620

-0,517

-0,588

—0,999

+0,429

+0,570

—

1,125

+ М25

+0,438

—0,438

+ 0,746

— 1,643

+0,897

+0,666

—0,873

—0,296

+0,503

— 1

+ 1

— 1

+ 1

—1

+ 1

—0,351

+0,351

—0,543

+0,543

+0,458

—0,458

+0,421

—0,421

+0,180

—0,180

-l0,843

—0,843

—2,303

+0,791

+ 1,545

—0,884

—0,783

+ 1,667

—

1,673

+2,063

—0,390

+ 1,054

—2,910

+ 1,856

—0,331

—0,325

—2,202

-1-2,858

+2,433

—2,779

+0,244

+ 0,186

—2,395

+2,311

—0,063

—3,576

+3,113

+0,526

+0,14

—0,17

+0,04

+0,14

—0,04

—0,09

—0,66

+0,20

+0,46

+ 0,38

—0,38

0,00

+0,21

+0,22

—0,48

+0,06

—0,38

+ 1,41

— 1,26

—0,16

+0,65

—0,27

—0.59

+0!07

+0,78

-0,25

—0,23

+0,264

+2,05

—2,289

+0,62

+0,137

+ 1,86

+0,881

hkw = —6,64

2у

= 6,64

10—2296

С учетом данных, приведенных в табл. 60, получим окончатель-

ное выражение весовой функции для длины стороны 5—7:

= AS

—0,351 (2) + 0,351 (3) — 0,543 (5) + 0,543 (6) +

+ 0,458 (13) — 0,458 (14) + 0,421 (17) -0,421 (18) +

+ 0,180 (20) —0,180 (22) + 0,843 (24) —0,843 (25).

Коэффициенты условных уравнений и весовых функций сведем

в табл. 61. Нижняя строка, в которой даны значения коррелат, и

последний столбец, в котором приведены поправки в направления,

заполняются после решения системы нормальных уравнений кор-

релат.

§ 44. Составление и решение нормальных уравнений

коррелат. Вычисление поправок направлений

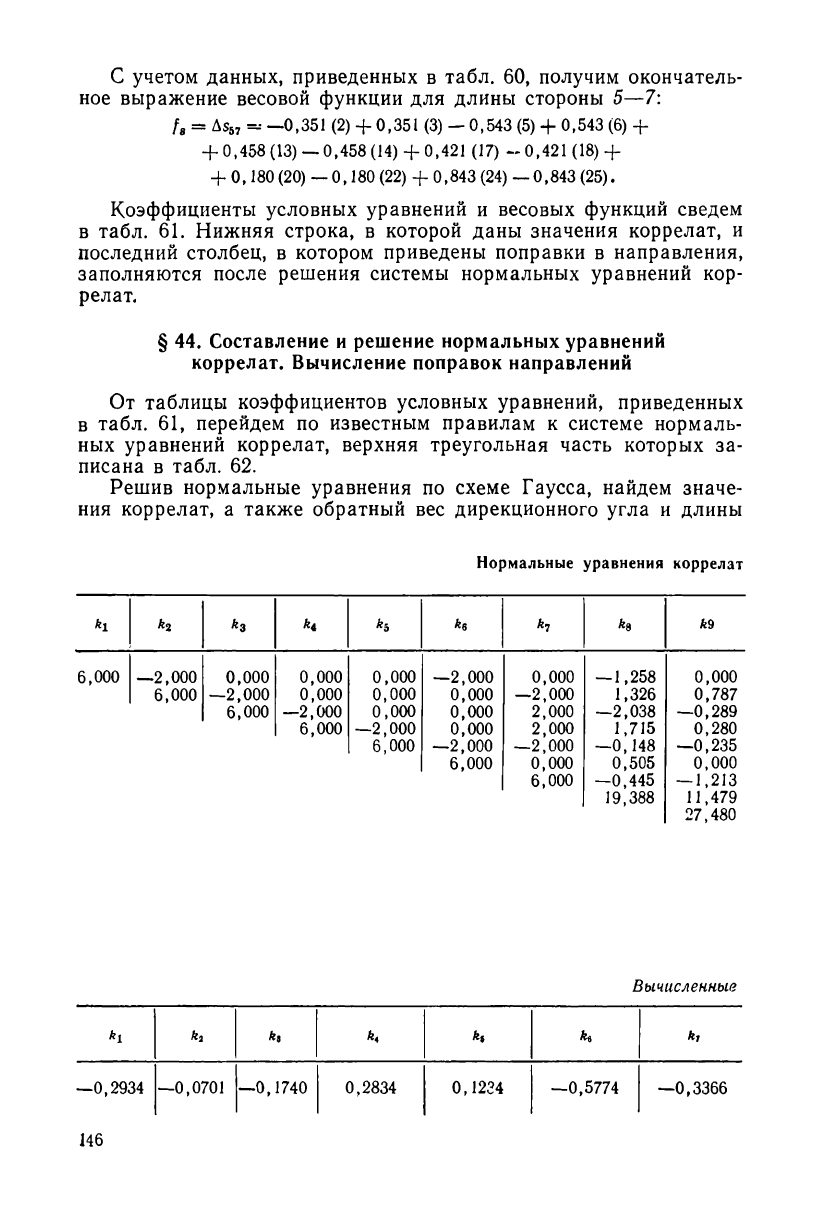
От таблицы коэффициентов условных уравнений, приведенных

в табл. 61, перейдем по известным правилам к системе нормаль-

ных уравнений коррелат, верхняя треугольная часть которых за-

писана в табл. 62.

Решив нормальные уравнения по схеме Гаусса, найдем значе-

ния коррелат, а также обратный вес дирекционного угла и длины

Нормальные уравнения коррелат

*з *4

*5 *7

Ад

6,000

—2,000 0,000 0,000

0,000

—2,000

0,000

— 1,258

0,000

6,000

—2,000 0,000 0,000 0,000

—2,000

1,326 0,787

6,000

—2,000

0,000

2,000

—2,038

—0,289

6,000

—2,000

0,000

2,000 1,715 0,280

6,000

—2,000

—0,148

—0,235

6,000

0,000

0,505

0,000

6,000

6,000 —0,445

— 1,213

6,000

19,388

11,479

27,480

Вычисленные

кг

Л/

—0,2934

—0,0701

—0,1740

0,2834 0,1234

—0,5774

—0,3366

146

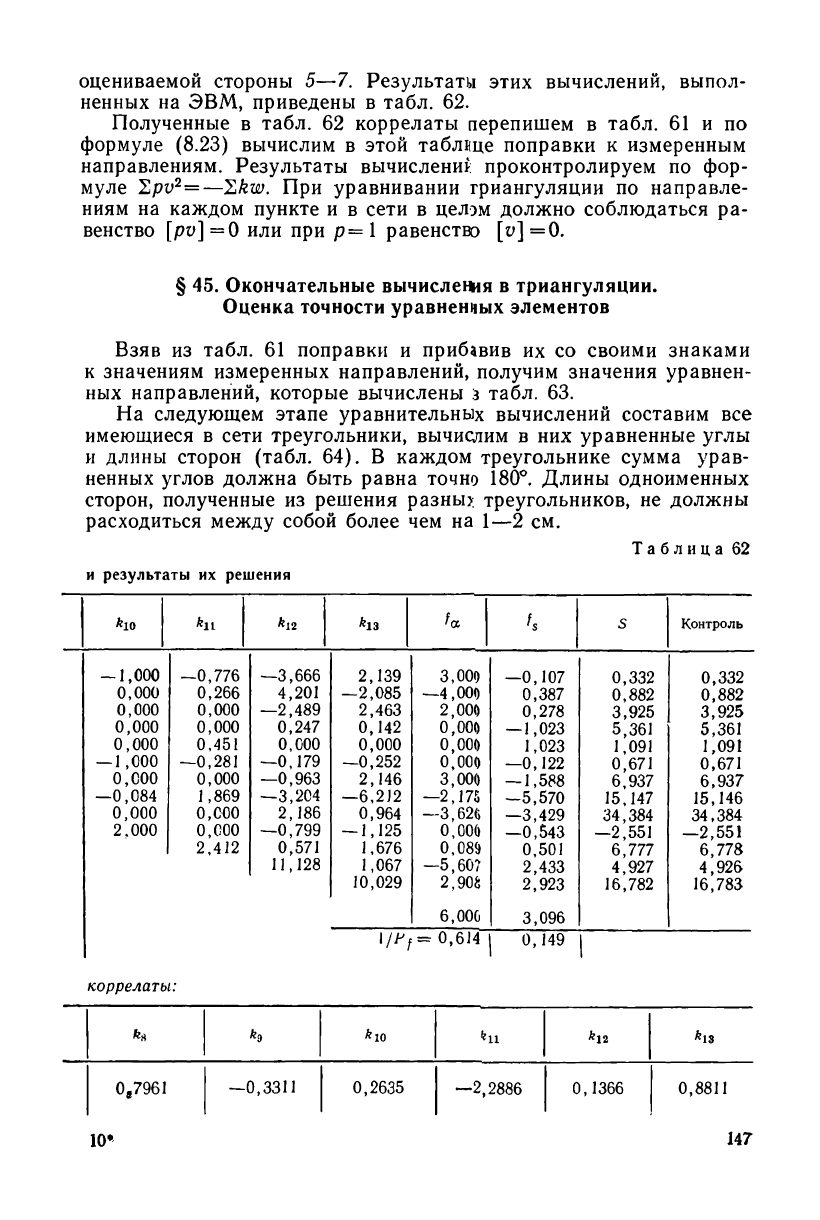
оцениваемой стороны 5—7. Результаты этих вычислений, выпол-

ненных на ЭВМ, приведены в табл. 62.

Полученные в табл. 62 коррелаты перепишем в табл. 61 и по

формуле (8.23) вычислим в этой таблице поправки к измеренным

направлениям. Результаты вычисление проконтролируем по фор-

муле 2ри

=—l>kw. При уравнивании триангуляции по направле-

ниям на каждом пункте и в сети в целэм должно соблюдаться ра-

венство [pv]= 0 или при р=

равенство [и]=0.

§ 45. Окончательные вычисления в триангуляции.

Оценка точности уравненных элементов

Взяв из табл. 61 поправки и прибавив их со своими знаками

к значениям измеренных направлений, получим значения уравнен-

ных направлений, которые вычислены :з табл. 63.

На следующем этапе уравнительных вычислений составим все

имеющиеся в сети треугольники, вычислим в них уравненные углы

и длины сторон (табл. 64). В каждом треугольнике сумма урав-

ненных углов должна быть равна точно 180°. Длины одноименных

сторон, полученные из решения разные треугольников, не должны

расходиться между собой более чем на 1—2 см.

Таблица 62

и результаты их решения

*и *13

Контроль

-1,000 —0,776

—3,666

2,139

3,000

—0,107

0,332

0,000

0,266

4,201

—2,085

—4,001)

0,387

0,882

0,000 0,000 —2,489

2,463

2,000

0,278

3,925 3,925

0,000 0,000

0,247

0,142

0,000

— 1,023

5,361

0,000 0,451 0,G00

0,000

1,023 1,091 1,091

— 1,000

—0,281

—0,179

—0,252

0,000

—0,122

0,671 0,671

0,000

0,000 —0,963

2,146

3,000

— 1,588

6,937

—0,084 1,869

—3,204

—6,212

—2,175

-5,570

15,147 15,146

0,000 0,000 2,186

0,964 —3,62*

—3,429

34,384

34»384

2,000

0,000 —0,799

— 1,125

0,000

—0,543 —2,551 —2,551

2,412

0,571

1,676 0,089

0,501

6,777

6,778

11,128

1,067

—5,60?

2,433

4,927 4,926

10,029

2,908

2,923

16,782

16,783

6,00G

3,096

= 0,614 1

0,149

коррелаты:

ft*

*п

*13

0,7961

—0,3311

0,2635

—2,2886

0,1366 0,8811

10*

147

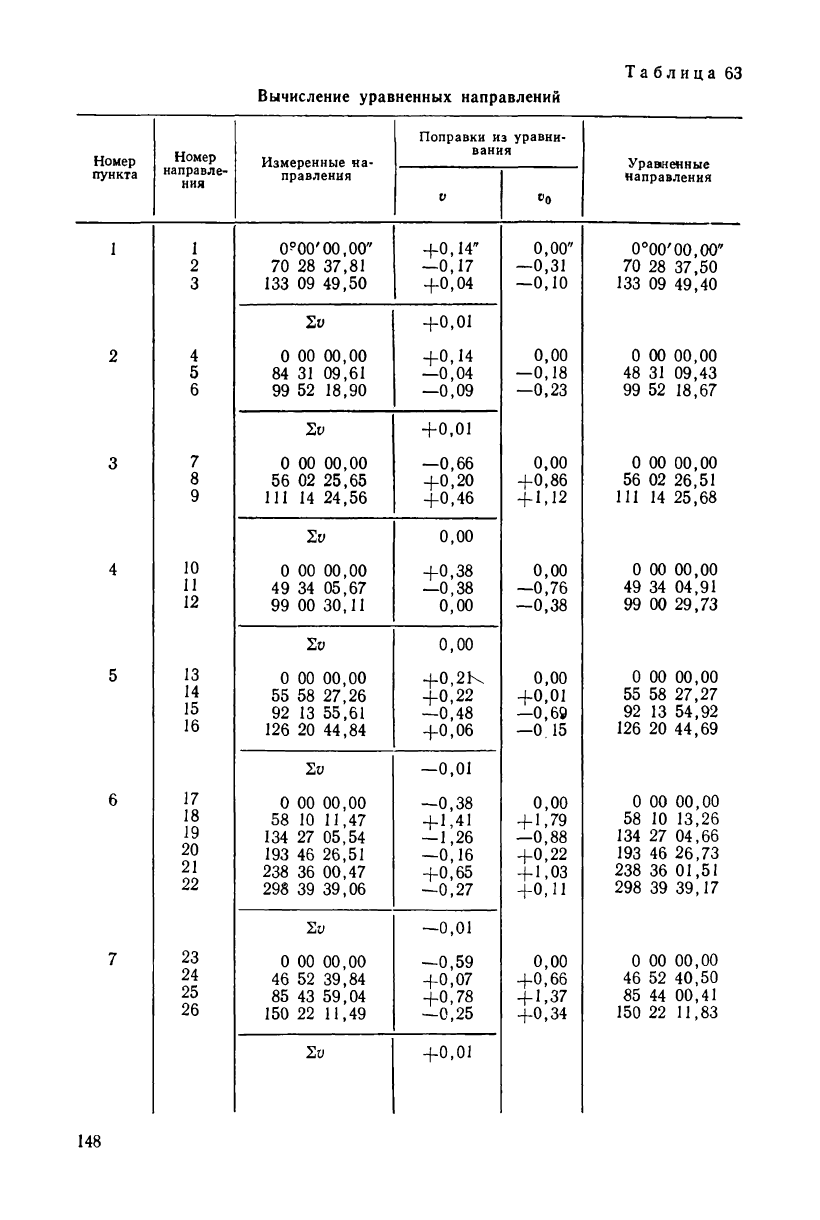
Таблица 78'

Вычисление уравненных направлений

Номер

Измеренные на-

правления

Поправки из уравни-

вания

пункта

направле-

ния

Измеренные на-

правления

00'00,00"

70 28 37,81

133 09 49,50

+0,14"

—0,17

+0,04

0,00"

—0,31

—0,10

+0,01

0 00 00,00

84 31 09,61

99 52 18,90

+0,14

—0,04

—0,09

0,00

—0,18

—0,23

+0,01

0 00 00,00

56 02 25,65

111 14 24,56

—0,66

+0,20

+0,46

0,00

+0,86

+ 1,12

0,00

0 00 00,00

49 34 05,67

99 00 30,11

+0,38

—0,38

0,00

—0,76

—0,38

2а

0,00

0 00 00,00

55 58 27,26

92 13 55,61

126 20 44,84

+0,2К

+0,22

—0,48

+0,06

0,00

+0,01

—0,69

—0 15

—0,01

0 00 00,00

58 10 11,47

134 27 05,54

193 46 26,51

238 36 00,47

298 39 39,06

—0,38

+ 1,41

— 1,26

—0,16

+0,65

—0,27

0,00

+ 1,79

—0,88

+0,22

+ 1,03

+0,11

—0,01

0 00 00,00

46 52 39,84

85 43 59,04

150 22 11,49

—0,59

+0,07

+0,78

-0,25

0,00

+0,66

+ 1,37

+0,34

+0,01

Уравненные

направления

0°00'00,00"

70 28 37,50

133 09 49,40

О 00 00,00

48 31 09,43

99 52 18,67

О 00 00,00

56 02 26,51

111 14 25,68

О 00 00,00

49 34 04,91

99 00 29,73

О 00 00,00

55 58 27,27

92 13 54,92

126 20 44,69

О 00 00,00

58 10 13,26

134 27 04,66

193 46 26,73

238 36 01,51

298 39 39,17

О 00 00,00

46 52 40,50

85 44 00,41

150 22 11,83

-148