Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

2.9 The reciprocal lattice 39

in terms of a position vector, is also known as the direct lattice. This distinction is

necessary to maintain clarity and keeps the discussion tractable going forward.

The central feature of a lattice is periodicity or regularity. In the study of periodic

order, Fourier analysis naturally comes to mind. A case in point is the study of

periodic signals; one can view the signal in the time domain and also view the

signal in the frequency domain by employing Fourier analysis. Our objective in

this section is to apply Fourier analysis to the study of the lattice in order to gain

additional insights.Without much ado, the reciprocal lattice is the discrete Fourier

transform of the direct lattice.

An elementary way to view the existence of a reciprocal lattice is to recall that

numbers, functions, and matrices all have reciprocal equivalents, generally related

by [X

−1

]·[X ]=1, where X can symbolize numbers, functions, and matrices

and [X

−1

] is the reciprocal equivalent. Similarly, temporal space has frequency

domain as its reciprocal; and the direct lattice (which is nothing more than a position

space with periodicity) has the reciprocal lattice has its reciprocal equivalent. The

reciprocal lattice satisﬁes the basic relation

iK·R

= 1, (2.31)

where K is the set of wavevectors that determine the sites of the reciprocal lattice

points and R is the Bravais lattice position vector as usual. The basic relation

originates from the Fourier analysis of the direct lattice. The reciprocal lattice

is a concept of paramount importance and provides fundamental insight into the

behavior of electrons in crystalline solids. In three dimensions theprimitive vectors

of the reciprocal lattice (b

, b

, and b

) are determined from the primitive vectors

of the direct lattice:

= 2π

× a

· (a

× a

)

, b

= 2π

× a

· (a

× a

)

, b

= 2π

× a

· (a

× a

)

(2.32)

However, our main interests are in two dimensions for the description of the lat-

tice of graphene and carbon nanotubes. Quite surprisingly, Eq. (2.32) requires

some care to scale down to two dimensions primarily because the cross prod-

uct is deﬁned only in three (and some select higher) dimensions. To derive the

reciprocal lattice vectors in two dimensions, let us consider a 2D plane deﬁned

by the vectors a

and a

; the corresponding reciprocal vectors are b

and b

We have to train our attention to keep track of four lattice distinctions: the crystal lattice, the

Bravais lattice, the direct lattice, and the reciprocal lattice. These terms can be mixed together to

form stimulating brain teasers, because they sometimes mean the same thing. For example, the

direct lattice is always a Bravais lattice, and the reciprocal lattice is itself always a Bravais lattice,

but yet the reciprocal lattice is not the same as the direct lattice. Just like the nuances of any

language, practice and familiarity are required, and afterwards it all makes sense.

An educational derivation of the reciprocal lattice as the Fourier transform of the direct lattice can

be found in several texts, including M. Dove, Structure and Dynamics: An Atomic View of

Materials (Oxford University Press, 2003), Chapter 4.

40 Chapter 2 Electrons in solids: a basic introduction

Initially, we might be tempted to simply set a

= 0, but the result is meaning-

less (the denominator of Eq. (2.32) vanishes). To resolve this dilemma, we need

to rethink what two dimensions mean mathematically. Geometrically, all mat-

ter exists in a 3D space regardless of whether the matter is a skinny molecule

or a gigantic mountain. When we speak of a 2D material or lattice, what is

actually meant is that the lattice is restricted to a plane with vanishing thick-

ness, where the vanishing thickness is an approximation for the relatively small

thickness the lattice actually possesses (relative to its width and length). For

the 2D plane of interest, the vanishing thickness approximation entails that the

vectors a

and a

have zero components in the third dimension. Furthermore,

the vector a

exists only in the third dimension, that is, it is ﬁnite in the third

dimension but vanishes in the other dimensions. Imposing these conditions on

Eq. (2.32) allows it to be rewritten elegantly in two dimentions by utilizing vector

operators:

= 2π

)

det(a

, a

)

, b

= 2π

(−a

)

det(a

, a

)

, (2.33)

where R

is an operator that rotates the vector clockwise by 90

◦

(coordinate axis

remains ﬁxed) and det is the determinant, which geometrically is the area of the

parallelogram formed by a

and a

and serves as a normalization factor. Since

the rotation operator may not be familiar to some readers, let us look at a simple

example. If vector v = v

ˆx+v

ˆy, then R

(±v) =±(v

ˆx−v

ˆy). From the rotation

operator, it is evident that the reciprocal lattice primitive vectors are either normal

or parallel to the direct lattice primitive vectors, corresponding to b

· a

= 2πδ

where δ

is the Kronecker delta function (δ

= 1 if and only if i = j, and δ

= 0

if i = j).

Some properties of the reciprocal lattice

(i) The reciprocal lattice is always a Bravais lattice, given that the direct lattice

is always a Bravais lattice. However, it might be a different Bravais lattice

compared with the original Bravais lattice in real space.

(ii) The reciprocal of the reciprocal lattice is the original direct lattice.

(iii) The direct lattice is measured in terms of a position vector R with units of

length; the reciprocal lattice is measured in terms of the wavevector K with

units of 1/length.

(iv) If s is the area of the direct lattice primitive cell, then (2π)

/s is the area of

the reciprocal lattice primitive cell.

(v) The direct lattice exists in real space or position space; the reciprocal lat-

tice exists in reciprocal space, which is sometimes called the Fourier space,

momentum space, or simply k-space. This is because the crystal momentum

is directly proportional to the wavevector.

2.9 The reciprocal lattice 41

(vi) The direct lattice can be viewed with a high-resolution electron microscope

(as in Figure 2.7b), the reciprocal lattice is often characterized via X-ray

diffraction patterns.

First Brillouin zone

The ﬁrst Brillouin zone is a central concept in the theory of solids, particularly

in the description of the band structure of electrons and other fundamental exci-

tations

that exist within the solid. We previously discussed the ﬁrst Brillouin

zone in the context of the Kronig–Penney model. An equivalent but more basic

deﬁnition is available based on the attributes of the reciprocal lattice: the Wigner–

Seitz primitive cell of the reciprocal lattice is the ﬁrst Brillouin zone. The standard

convention is that the ﬁrst Brillouin zone is the terminology exclusively used in the

context of the reciprocal lattice, while the Wigner–Seitz terminology is used in the

context of thedirect lattice. Higher Brillouin zones also exist; however, those zones

duplicate the information already present in the ﬁrst Brillouin zone. As a result,

casual usage of the term Brillouin zone often implies the ﬁrst Brillouin zone in

particular.

An example: the hexagonal lattice

Let us consider the 2D hexagonal lattice to demonstrate the construction of the

reciprocal lattice and the ﬁrst Brillouin zone. The hexagonal lattice in direct

space and the associated Wigner–Seitz cell are shown in Figure 2.13a. A pair

of symmetrical direct lattice primitive vectors from Eq. (2.30)are



√



, a



√

, −



The reciprocal lattice primitive vectors can be computed from Eq. (2.33):



2π

√

2π



, b



2π

√

, −

2π



. (2.34)

The resulting reciprocal lattice generated from sweeping b

and b

by integer

multiples and the associated ﬁrst Brillouin zone are shown in Figure 2.13b.

The Wigner–Seitz cell and the ﬁrst Brillouin zone are hexagons, displaying the

hexagonal symmetry of the lattices. It is clearly visible from the ﬁgure that the

reciprocal lattice and ﬁrst Brillouin zone are rotated 90

◦

with respect to the direct

lattice.

Besides electron excitations, there exist collective excitations such as lattice vibrations called

phonons, electron density vibrations called plasmons, and spin vibrations called magnons. The

Brillouin zone is useful in describing all these excitations.

42 Chapter 2 Electrons in solids: a basic introduction

(a)

(b)

Fig. 2.13

(a) The hexagonal lattice and Wigner–Seitz cell (gray hexagon). (b) The corresponding

reciprocal lattice, primitive vectors, and the ﬁrst Brillouin zone (gray hexagon).

2.10 Summary

In this chapter we have explored at a very introductory level the quantum mechan-

ical description of electrons in solids and the periodic structure found in crystalline

solids. This introduction is more or less meant to serve as a refresher for those with

prior quantum mechanics background. Nonetheless, the narrative is such that all

the concepts and techniques developed are accessible to those with no prior course

in quantum mechanics. The intuition developed and the understanding gained will

be put to work in the development of the band structure of graphene and CNTs in

Chapters3and4respectively.

2.11 Problem set

2.1. Electron scattering by a step potential barrier: a simple model to illustrate the

ideas of reﬂection and transmission.

Consider the step potential barrier shown in Figure 2.14.

(a) Write the general solution for the electron wavefunction for each region

(I, II). Note that the wavevector will be different in each region.

(b) What is the expression for k in each region in terms of the energy of that

region?

barrier with energy E > U

. We want to determine the fraction of the

electron that is reﬂected and transmitted by the barrier, a very important

concept characteristic of all wave phenomena. What are the boundary

conditions at x = 0?

(d) From the boundary conditions, determine the transmission and reﬂection

probabilities, which are respectively deﬁned as

T =



and  =



−



,  + T = 1,

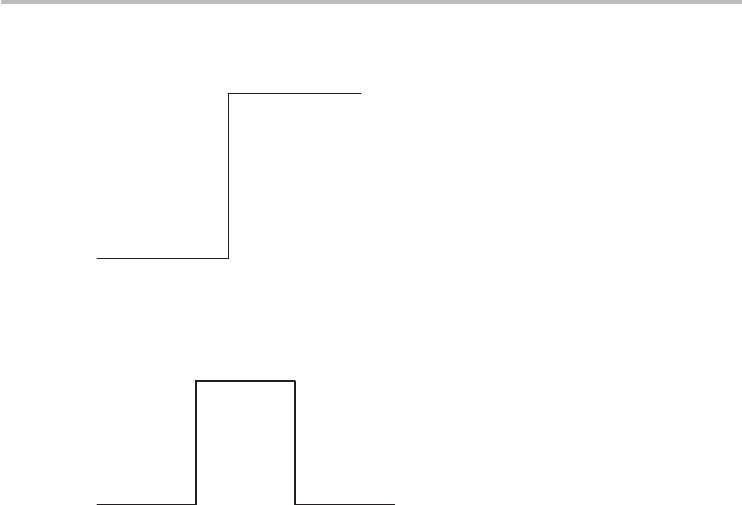
2.11 Problem set 43

III

x = 0

U = 0

U =U

Fig. 2.14 Step potential barrier.

III

x = 0

U = 0

U = U

U = 0

III

x = w

Fig. 2.15 Rectangular potential barrier.

where ψ

is a right-moving component of ψ

and ψ

−

is a left-moving

component of ψ

(e) Repeat parts (c) and (d) for an electron wave incident with energyE < U

(f) For a barrier potential and width of U

= 0.3 eV and w = 1 nm, plot the

transmission probabilities for electron waves with E > U

, and E < U

(g) Assuming the electron is a classical particle like a ball and the potential

barrier can be thought of as a wall, in this case sketch the transmission

probability of the classical particleand superimpose iton the transmission

probabilities from (f). What are the key differences, if any?

2.2. Electron scattering by a rectangular potential barrier: another simple model

to illustrate the ideas of reﬂection and transmission.

Consider the potential barrier shown in Figure 2.15.

(a) Write the general solution for the electron wavefunction for each region

(I, II, III). Note that the wavevector will be different in each region.

(b) What is the expression for k in each region in terms of the energy of that

region?

with energy E > U

. We want to determine the fraction of the electron

that makes it through the barrier, a very important concept characteristic

of all wave phenomena. What are the boundary conditions at x = 0 and

x = w?

44 Chapter 2 Electrons in solids: a basic introduction

(d) From the boundary conditions, determine the transmission and reﬂection

probabilities, which are respectively deﬁned as:

T =



III



and  = 1 − T,

where ψ

is a right-moving component of ψ

(e) For a barrier potential and width of U

= 0.3 eV and w = 1 nm, plot the

transmission probability.

(f) Assuming the electron is a classical particle like a ball and the potential

barrier can be thought of as a wall, in this case sketch the transmission

probability of the classical particle and compare it with your result from

(e). What is the key difference, if any?

Bonus questions

(g) Newton’s laws (classical mechanics) are often beaten up in quantum

mechanics, but what is often not emphasized enough is that classical

electromagnetism is still very useful. If you are familiar with Electromag-

netism 101, you can solve a number of signiﬁcant quantum mechanical

problems almost by inspection by borrowing ideas from electromagnetic

wave theory.

From part (e), determine the conditions that yield resonant transmission

(T = 1 peaks). This is a familiarresult from electromagneticpropagation.

(h) Solving the mathematics in quantum mechanics problems can often be

tedious and “hard,” but this is not the most important part of learning.

More important is the physics behind the equations and results.

From part (g), what is the physical reason behind the resonant peaks?

(Hint: There is a deep universal symmetry here: the reason for (h) is

the same reason why there is resonance in all wave phenomena, such as

electromagnetic, acoustic, seismic, and optical waves.)

2.3. A qualitative comparison of the bandgap of CNTs and graphene nanoribbons

(GNRs).

You do not need to know what bandgap refers to in order to solve this

problem. In brief, the bandgap is a fundamental property of all solids that

informs us of whether the solid is an insulator, semiconductor, or metal;

that is, how well it can conduct electricity. We are interested in comparing

the bandgaps of CNTs and GNRs, at least qualitatively, to give us some

basic insight as to which one has the lower or higher bandgap for the same

dimensions. This is very important for electronic devices, as we will learn

during the course of this book.

Consider an electron in a 1D empty solid of width w and inﬁnite potential

barriers at the edges. Qualitatively, this is the simplest model one can use for

2.11 Problem set 45

CNTs or GNRs. It is certainly not accurate, but is good enough to provide

important basic insights regarding bandgap dependency on the nanomaterial

width.

(a) Write the general expression for the electron wavefunction.

For GNRs we will employ the usual boundary conditions ψ(0) =

ψ(w ) = 0. For CNTs we will employ what is known as periodic bound-

ary conditions applicable to conditions applicable when the beginning

of the structure, touches the end of the structure such as a cylinder. The

applicable boundary conditions are ψ(0) = ψ(w) = e

ikw

ψ(0).

(b) Determine the solution for the wavevector and the allowed energies in

the GNR model.

can be thought of as directly related to the bandgap. Denote this energy

as E

g_min

(d) Repeat (b) for the CNT model.

(e) What is the lowest wavevector and energy of this electron in the CNT

model? This energy can be thought of as directly related to the bandgap.

Denote this energy as E

c_min

(f) By what factor is E

g_min

larger or smaller than E

c_min

(g) So far, what we have been trying to determine is how the boundary

conditions affect the bandgaps of nanotubes compared with nanoribbons.

Another direct way to determine this is to look at experimental data or

semi-empirical equations for the bandgap. For nanoribbons, consider the

semi-empirical equation for the bandgap provided by Han et al.

For

nanotubes, employ the relation E

(eV) = 0.9/d

(nm). For a width of

20 nm, by what factor is the bandgap of nanotubes larger or smaller than

nanoribbons? Compare with the factor determined in part (f).

2.4. The reciprocal lattice vectors.

(a) Prove that, given a set of primitive unit vectors a

, a

, and a

, the recip-

rocal lattice vectors deﬁned in Eq. (2.32) satisfy the reciprocity condition

of e

iK·R

= 1.

2.5. How many Bravais lattices are there in 1D space?

2.6. Crystal structure.

(a) Which of the 2D lattices in Figure 2.16 is not a Bravais lattice? A, B, C,

or D?

(b) Determine its underlying Bravais lattice and draw two different primitive

unit cells for that lattice. How many lattice points are there?

M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Energy band-gap engineering of graphene

nanoribbons. Phys. Rev. Lett., 98 (2007) 206805.

46 Chapter 2 Electrons in solids: a basic introduction

(A) (B)

Fig. 2.16 The 2D lattices for Problem 2.6.

(d) Draw the reciprocal lattice.

(e) Sketch the ﬁrst Brillouin zone.

2.7. Bravais and reciprocal lattices.

(a) Construct the reciprocal lattice for the ﬁve 2D Bravais lattices.

(b) Construct the Brillouin zone for all ﬁve reciprocal lattices.

3 Graphene

Dream your dreams and may they come true.

Felix Bloch (developed the theory describing

electrons in crystalline solids)

3.1 Introduction

The objective of this chapter is to describe the physical and electronic structure of

graphene. Familiarity with concepts such as the crystal lattice and Schrödinger’s

quantum mechanical wave equation discussed in Chapter 2 will be useful. The

electronic band structure of graphene is of primary importance because (i) it is

the starting point for the understanding of graphene’s solid-state properties and

analysis of graphene devices and (ii) it is also the starting point for the under-

standing and derivation of the band structure of CNTs. We begin by broadly

discussing carbon and then swiftly focus on graphene, including its crystal

lattice and band structure. This chapter concludes on the contemporary topic

of GNRs.

Carbon is a Group IV element that is very active in producing many molecular

compounds and crystalline solids. Carbon has four valence electrons, which tend

to interact with each other to produce the various types of carbon allotrope.

elemental form, the four valence electrons occupy the 2s and 2p orbitals,

illustrated in Figure 3.1a. When carbon atoms come together to form a crystal,

one of the 2s electrons is excited to the 2p

orbital from energy gained from

neighboring nuclei, which has the net effect of lowering the overall energy of the

system. Interactions or bonding subsequently follow between the 2s and 2p orbitals

of neighboring carbon atoms. In chemistry, these interactions or mixing of atomic

Allotropes are different structural modiﬁcations of an element in the same phase of matter, e.g.

different solid forms.

An orbital is essentially the electron wavefunction that informs us of the electron distribution

around the nucleus. The elemental orbitals have speciﬁc distributions often graphed in standard

chemistry texts. When elemental orbitals mix or hybridize, they form new orbitals with new

electron distributions.

48 Chapter 3 Graphene

Table 3.1. Allotropes of graphene

Dimension 0D 1D 2D 3D

Allotrope C

buckyball Carbon nanotubes Graphene Graphite

Structure Spherical Cylindrical Planar Stacked planar

Hybridization sp

Electronic properties Semiconductor Metal or semiconductor Semi-metal Metal

1s 2s

(a) (b)

(c)

Fig. 3.1 The arrangement of electrons and their relative spin in (a) elemental carbon and

(b) graphene. (b) The s and two of the p orbitals of the second shell interact covalently to

form three sp

hybrid orbitals. (c) Illustration of the orbitals.

0.14 nm

Fig. 3.2 Remarkable transmission electron aberration-corrected microscope (TEAM) image of

graphene vividly showing the carbon atoms and bonds in the honeycomb structure

(courtesy of Berkeley’s TEAM05, 2009).

orbitals is commonly called hybridization, and the new orbitals that are formed are

referred to as hybrid orbitals. The existence of multiple ﬂavors of hybridization in

carbon is what leads to the different allotropes shown in Table 3.1.

Graphene is a planar allotrope of carbon where all the carbon atoms form cova-

lent bonds in a single plane. The planar honeycomb structure of graphene has been

observed experimentally and is shown in Figure 3.2. Graphene can be consid-

ered the mother of three carbon allotropes. As illustrated in Figure 3.3, wrapping