Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

2 Electrons in solids: a basic

introduction

Free your mind.

2.1 Introduction

The central purpose of this book is to understand the properties of electrons in CNTs

and graphene. A good understanding is of utmost importance because it enables us

to make electronic devices and engineer the performance of the devices to satisfy

our desires. These devices can include, for example, sensors, diodes, transistors,

transmission lines, antennas, and electron emission devices. In addition, the devices

made out of carbon nanomaterials are being considered as building blocks for

future applications broadly referred to as nanoelectronics, which includes circuits

and systems. The technology to make nanomaterials and related devices is called

nanotechnology.

To accomplish our central purpose, it is essential that we are familiar with

the mathematical techniques and physical ideas behind the theory of electrons,

particularly in solids. Speciﬁcally, in order to understand and describe the behavior

of electrons in a solid requires consideration of:

(i) The general quantum mechanical wave nature of electrons.

(ii) The periodic arrangement of atoms in crystalline solid matter, which is

frequently called the crystal structure or lattice.

The introductory discussion of electrons in solids in this chapter will proceed

in a manner that is beneﬁcial for developing intuition, by considering an introduc-

tory quantum mechanical description of electrons, and subsequently exploring the

crystal structure. Our attention throughout the chapter will be focused on the math-

ematical techniques, central ideas, and main results regarding electrons in solids. In

view of the fact that quantum mechanics and solid-state physics are themselves fun-

damental disciplines of physics of great breadth and depth, this chapter is primarily

intended as an elementary review of the minimum basic concepts and techniques

in the quantum mechanical description of electrons in solids. The understanding

and intuition developed in this chapter will be applied throughout the entire book.

20 Chapter 2 Electrons in solids: a basic introduction

References will be provided along the way for readers that would enjoy a more

detailed coverage of the basic concepts. Readers already familiar with the physics

concepts and techniques are invited to advance to the next chapter.

2.2 Quantum mechanics of electrons in solids

Understanding how electrons behave in a solid is central to the development of

any solid-state electronic device. This understanding is what makes it possible to

control electrons by external forces and to obtain interesting characteristics. To

guide our intuition we will ﬁrst review how electrons behave in free space and

how their behavior changes when they are in a solid. By behavior we are mostly

interested in their most fundamental properties, which are their wavevector and

energy. Together these two properties give us an idea of how free or excited the

electrons are behaving. The more excited they are, the easier it will be to control

them. Energy and wavevector are actually related, and this relationship is com-

monly called the dispersion or band structure. It is not an overstatement to assert

that the dispersion is the most important and central characteristic that describes

the behavior of electrons in a crystalline solid. Indeed, it is the dispersion or band

structure that we seek to derive and understand in this chapter, and subsequently

inChapters3and4.

It is worthwhile noting that there are a gazillion

electrons present in typical

solids. For example, there exist on the order of 10

electrons/cm

if we consider

only the valence electrons in bulk metals. How can we accurately describe the

behavior of all these electrons in a solid? The simple answer is that we cannot

describe them all, at least not exactly. However, if the electrons have negligi-

ble or no interaction with each other, than the problem reduces to the case of

describing the behavior of one electron, which is by far a much simpler problem.

This is technically called the one-electron or independent electron approxima-

tion. Fortunately, this approximation is accurate in understanding the behavior of

electrons in the majority of solids of interest operating at room temperature. The

independent electron is an underlying approximation employed in all the electron

models developed in thischapter andin the entire textbook, unlessnoted otherwise.

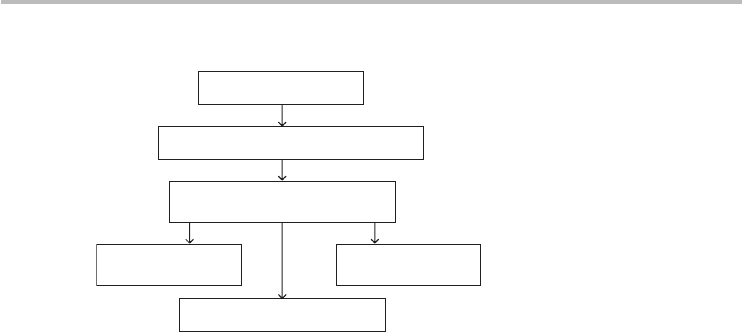
Figure 2.1 illustrates several one electron models in order of increasing complex-

ity.Thischapterwillexaminetheﬁrstthreemodelsintheﬁgure,andChapter3

will explore the tight-binding model for the development of the band structure of

graphene.

Since the electrons will be treated as waves, Schrödinger’s equation in its most

basic form will be employed to solve for their properties. For this purpose, we

assume the reader has at least a basic exposure to quantum mechanics at the level

Think of a very, very large number whose precise value is unnecessary to specify at this moment.

2.3 An electron in empty space 21

An electron in space

An electron in a finite empty solid

An electron in a solid with a

simple periodic potential

Ab-initio electron models

Nearly-free

electron model

Tight-binding

electron model

Fig. 2.1 Illustrative ﬂowchart of independent electron models. Arrows indicate increasing

complexity.

of an undergraduate modern physics course.

In general, the quantum mechanics

in this section and in the entire book is kept to a minimum, and much of the

understanding and intuition developed as we move ahead should still be accessible

to readers who are not familiar with quantum mechanics.

2.3 An electron in empty space

The simplest possible model of electrons is the model of a free electron in empty

space. Understanding this model is the ﬁrst step towards our goal of gaining deeper

insight and understanding of electrons in real crystalline solids. In principle, empty

space is essentially the limiting case of an inﬁnite force-free solid. Free electrons

are electrons that have no forces or potential acting on them and hence, they are

free. Even though we are considering a single free electron in these introductory

models, the mathematical formalism developed and knowledge acquired applies

directly to realistic solids with a much larger number of electrons, provided the

electrons have negligible interaction with one another, which is often the case at

room temperature.

In this simple pedagogical model of a free electron in space we seek to

determine the energy–wavevector relationship or dispersion by solving the time-

independent

Schrödinger equation. In one-dimensional (1D) space measured by

A widely read modern physics textbook is D. Giancoli, Physics for Scientists and Engineers with

Modern Physics, 4th edn (Prentice Hall, 2008). For introductory graduate-level coverage of

quantum mechanics see D. A. B. Miller, Quantum Mechanics for Scientists and Engineers

(Cambridge University Press, 2008).

The time-independence terminology can be quite confusing to the new aspiring quantum mechanic

by suggesting there is no time dependence, which is certainly not the case for a wave. In the

language of quantum mechanics, what is meant is that the probabilistic properties of the system are

time invariant (to borrow jargon from signals theory).

22 Chapter 2 Electrons in solids: a basic introduction

the variable x, the Schrödinger equation is

H ψ(k, x) = E(k)ψ(k, x) (2.1)



−



∂

∂x

+ U (x)



ψ(k, x) = E(k)ψ(k, x), (2.2)

where H is the Hamiltonian operator with its explicit form in the parentheses of

Eq. (2.2),

ψ is the electron wavefunction, E is the electron total energy, and k

is the wavevector.  is the reduced Planck’s constant, m is the electron mass, and

U (x) = 0 for all x for the free-electron model. This is a frequently occurring

differential equation with a general solution in the form of exponentials:

ψ(k, x) = Ae

ikx

, (2.3)

where k can take on arbitrary real positive or negative values and where the

complex exponential with an amplitude A is considered a plane wave because it

oscillates similar to electromagnetic waves in space. This is easily seen by expand-

ing the exponential in terms of trigonometric functions. To determine the energy of

the electrons we employ two relations. The ﬁrst relation from classical mechanics

treats the electron as a particle with an energy given in terms of its momentum:

E =

, (2.4)

where p is the momentum of the particle. The second relation is the de Broglie

wave-duality postulate, which assigns wave-like behavior (vis-à-vis k) to a particle

with momentum p, p = k.

Substituting p = k into Eq. (2.4), the energy–

wavevector relationship for a free electron in space leads to the celebrated parabolic

dispersion:

E =



. (2.5)

For three-dimensional (3D) space, it is a straightforward exercise to show that

the dispersion is essentially the same with the wavevector k replaced by the 3D

wavevector K, and K

= k

+ k

In summary, the key observations we gain by examining free electrons in space

are that the electrons oscillate as plane waves with a continuous set of wavevectors

and, correspondingly, a continuous energy spectrum.The study of this pedagogical

The Hamiltonian operator acts on the wavefunction to produce the corresponding allowed energies.

As it is said “success has many fathers.” Louis de Broglie’s postulate of matter waves (his Ph.D.

thesis) was a generalization of Albert Einstein’s energy quanta theory of the photoelectric effect,

which itself builds on Max Planck’s blackbody quantization theory. All three were awarded (on

separate occasions) a Nobel Prize for their development of quanta and quantum mechanics.

2.4 An electron in a ﬁnite empty solid 23

model by itself is not particularly interesting; however, when we compare it with

the behavior of electrons in a ﬁnite solid we begin to develop intuition as to how

the solid environment perturbs the electrons and the general technique of solving

for the energy–wavevector dispersion.

2.4 An electron in a ﬁnite empty solid

We consider the next simplest model of electrons by reducing the empty inﬁnite

solid of the previous section to an empty ﬁnite solid of length L with a potential

illustrated in Figure 2.2 and mathematically described in one dimension as

U (x) =



0 for 0 < x < L

∞ elsewhere.

(2.6)

How the dispersion of electrons in this ﬁnite solid compares with the previous

model is the primary question of interest. This idealized model is also called by

phrases such as particle in a box or particle in an inﬁnite potential well. However,

a concern to keep in mind is that ﬁnite empty solids with inﬁnite potential walls

do not exist in nature. Nonetheless, the ﬁnite empty solid model is of great tech-

nical value because it shines light on our intuition about electrons in real solids

and it provides a basis for developing simple analytical dispersions of far more

complicated crystalline solids. In principle, this model is essentially the limiting

case of a solid in which the electrostatic force between the atomic nucleus and the

electrons under consideration is negligible.

Having convinced ourselves that this model is of value in developing insight, we

proceed with the analysis by solving Schrödinger’s equation (Eq. (2.2)) with the

potential given by Eq. (2.6). The general solution is given by complex exponential

functions indicative of an oscillating wave:

ψ(k, x) = Ae

ikx

+ Be

−ikx

. (2.7)

U=0

U=∞

∞–∞

U=∞

Fig. 2.2 The potential proﬁle that deﬁnes a 1D ﬁnite empty solid of length L.

24 Chapter 2 Electrons in solids: a basic introduction

The ﬁnite size of the solid imposes a boundary condition that places a restriction

on the wavefunction.

ψ(x = 0) = ψ(x = L) = 0. (2.8)

A hand-waving argument to justify these boundary conditions is that the electron

cannot escape from the solid since the inﬁnite potential exerts an inﬁnite force that

bounds the electron. As a consequence, the wavefunction and the probability of

ﬁnding the electron must vanish outside the solid.Applying the boundarycondition

at x = 0 requires B =−A, and simpliﬁes the wavefunction, ψ(k, x) = C sin kx,

where C is generally a complex constant to be determined shortly. The boundary

condition at x = L requires

k =

nπ

, n = 1, 2, 3, ..., (2.9)

where we have ruled out n = 0 because, for that case, ψ = 0 everywhere, implying

that the electron is not present in all space, which is a trivial case of no interest.

n is called a quantum number that indexes the allowed wavevectors. Substituting

for the wavevector into Eq. (2.5), the resulting energies are

E =

2mL

. (2.10)

The only remaining unknown is the amplitude C, which is determined from a

normalization condition, afﬁrming that the probability of ﬁnding the electron in

the box is unity:



∞

−∞

|ψ(x)|

dx =



|ψ(x)|

dx = 1, (2.11)

where |ψ(x)|

is interpreted as the probabilitydensity.The normalization condition

results in |C|=

√

2/L, or simply C =

√

2/L, if we consider only real-valued

numbers. The important physics gained from this analysis is as follows:

1. Dispersion quantization The electron wavevector and energy can only take

on discrete values owing to the ﬁnite size of the solid.

2. Zero-point energy The energy of the electron cannot vanish. The lowest pos-

sible energy, called the zero-point energy, occurs when n = 1. This minimum

energy is fundamentally due to the momentum–position uncertainty relation in

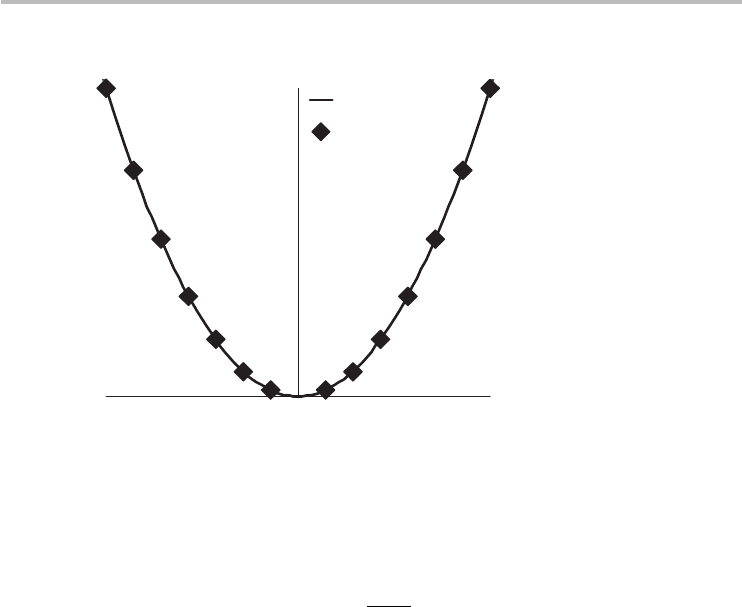
quantum mechanics. The dispersion is illustrated in Figure 2.3 and compared

with the free electron in space vividly showing the quantization due to spatial

conﬁnement. It is a straightforward exercise to show that the dispersion is read-

ily extended to a 3D empty ﬁnite solid by replacing the wavevector k with the

3D wavevector K, which leads to three independent quantum numbers, n

, n

2.4 An electron in a ﬁnite empty solid 25

electron in space

electron in solid

Fig. 2.3

Energy–wavevector dispersions of a free electron in space and in a ﬁnite solid.

and n

representing the boundary conditions from each spatial dimension. The

resulting 3D dispersion is

E =



2mL

+ n

). (2.12)

Compared with the 1D dispersion, the 3D dispersion contains the same physics

plus an additional physics called degeneracy, which is deﬁned as the case where

a different set of quantum numbers results in the same energy. For example, the

set of quantum numbers

, n

) = (1, 2, 3); (1, 3, 2); (3, 1, 2);

= (2, 1, 3); (2, 3, 1); (3, 2, 1)

result in the same energy and, therefore, are sixfold degenerate. In general, if m sets

of quantum numbers yield the same energy, this is called an m-fold degeneracy.

Degeneracy is an important concept, as we shall see throughout this book, and

often reﬂects the underlying geometrical symmetries

present in the system.

The utility of the simple parabolic dispersion obtained here cannot be overem-

phasized. It has been used successfully (with few modiﬁcations) to predict

and explain many of the properties of electrons from 3D solids such as bulk

semiconductors to 1D molecular solids such as CNTs.

Symmetry is a fundamental idea in quantum mechanics and solid-state physics and is of great value

in providing insight about how electrons conduct themselves in crystalline solids. Useful (and

compact) discussions can be found in H. Kroemer, Quantum Mechanics (Prentice Hall, 1994); and

N. W. Ashcroft and N. D. Mermin, Solid State Physics (Brooks/Cole, 1976).

26 Chapter 2 Electrons in solids: a basic introduction

2.5 An electron in a periodic solid: Kronig–Penney model

So far we have concerned ourselves with the behavior of an electron in an inﬁ-

nite and ﬁnite empty solid and become acquainted with the general nature of the

dispersion and energy quantization that comes about because of size conﬁnement.

However, real crystalline solids have a periodic arrangement of atoms that exerts

a force on electrons. Therefore, in reality, any electron in a solid cannot be com-

pletely free. In the pursuit of spatial freedom, an electron can, at best, be nearly

free. The paramount question now is: How does the periodic potential of the atoms

affect the behavior of an electron in a solid?

To address this question,we haveto consider how to model the periodic potential

ﬁeld in the solid or crystal lattice as it is sometimes called. The actual potential

ﬁeld can be determined from Coulomb’s law; however, for simplicity we shall

consider periodic delta potentials in a large 1D solid lattice with length L,as

shown in Figure 2.4, originally proposed by Kronig and Penney.

This simplicity

is fortunately mostly mathematical in nature while gracing us with insight into

much of the physics of electrons in real solids.



(E − U (x))ψ = 0. (2.13)

This is a well-studied differential equation with formal solutions that are described

by Bloch’s theorem in solid-state physics or equivalently by the much older

Floquet’s theorem of differential equations. These solutions are of the form

ψ(x) = u(x) e

ikx

, (2.14)

where u(x) is an amplitude modulating function with the periodicity of the lattice

potential, u(x) = u(x+a). Bloch’s theorem states that the wavefunction is periodic

with the length of the lattice, i.e. ψ(0) = ψ(L), which results in quantization of

the wavevector (as we have observed in the previous empty solid model):

ikL

= 1, → k =

2π

n, (2.15)

where n is an integer. To determine u(x) we consider one unit cell and examine

the space between the potentials when U (x) = 0, whence Schrödinger’s equation

reduces to

+ γ

ψ = 0, γ

2mE



. (2.16)

R. de L. Kronig and W. G. Penney, Quantum mechanics of electrons in crystal lattices. Proc. R.

Soc. (London) A, 130 (1931) 499–513.

2.5 Electron in a periodic solid 27

Cδ CδCδCδ

a0–a

≈

Cδ

≈

–L/2

Fig. 2.4 Kronig–Penney periodic potential in a solid of length L. C is the strength of the delta

function. Inside the solid, the electron wavefunction must satisfy Schrödinger’s equation

with a periodic potential U(x) = U(x + a), and the length of the solid is an integral

multiple of the unit cell.

Substituting Eq. (2.14) into Eq. (2.16) yields

+ 2ik

+ (γ

− k

)u = 0. (2.17)

This is a standard second-order linear differential equation with constant coefﬁ-

cients and has a solution given by

u(x) = (A cos γ x + b sin γ x)e

−ikx

(2.18)

subject to periodic boundary conditions that guarantee continuity for the u(x)

function and its slope:

u(0) = u(a). (2.19)

The continuity conditions of the slope involving delta potentials have to be treated

with care. We derive the appropriate boundary condition for the slope by integrating

the Schrödinger equation over a very small region 2 about x = 0:

−







−

dx +





−

Cδ(x)ψdx = E





−

ψdx. (2.20)

In the right-hand side (RHS) of the equation, ψ does not change appreciably if

the interval is inﬁnitesimal and can be assumed constant, ψ(0). Evaluating the

integrals gives



(

) − ψ



(

−

) −



Cψ(0) = 2Eψ(0). (2.21)

In the limit that  → 0, then 2Eψ(0) → 0, the equation simpliﬁes to



(

) − ψ



(

−

) =

2mC



ψ(0). (2.22)

28 Chapter 2 Electrons in solids: a basic introduction

Substituting for ψ (and its derivative) from Eq. (2.14) and simplifying yields



(

) − u



(

−

) + ik(u(

) − u(

−

)) =

2mC



u(0). (2.23)

Without any loss in accuracy, we can replace x = 

with x = 0 and replace

x = 

−

with x = a since u(x) is periodic with length a:



(0) = u



(a) +

2mC



u(0). (2.24)

Finally, substituting Eq. (2.18) into Eq. (2.19), and also into Eq. (2.24), results in

two simultaneous equations:

A (1 − e

−ika

cos γ a) = Be

−ika

sin γ a



ike

−ika

cos γ a +γ e

−ika

sin γ a − ik −





= B(γ e

−ika

cos γ a −ike

−ika

sin γ a − γ),

which can be solved by the method of substitution, resulting in the following

solution:

cos ka = cos γ a + P

sin γ a

γ a

, (2.25)

where P = maC/

. The solution is a transcendental equation that is not solvable

algebraically. One often has to resort to graphical or numerical techniques. In the

limit of zero potential (P = 0), the solution reduces to the case of a free electron

in a ﬁnite solid.

There are several ways to digest the solution. Let us start by graphing the RHS

of Eq. (2.25) as a function of γ a as is shown in Figure 2.5 (P = 5 for this example).

The RHS results in an oscillating function that is sometimes greater than +1 and

sometimes less than −1. Comparing this with the left-hand side (LHS) of Eq.

(2.25), which is restricted to values within ±1, we can conclude that only certain

values of γ a (and hence energy via Eq. (2.16)) that satisfy this restriction result

in allowed solutions of Eq. (2.25), and values that do not satisfy the restriction are

forbidden. As Kronig and Penney eloquently stated in their 1931 article:

the energy values which an electron moving through the lattice may have, hence form a

spectrum consisting of continuous pieces separated by ﬁnite intervals.

In other words, there are allowed energy bands separated by gaps, known as

bandgaps. To see this more vividly, the dispersion

is shown in Figure 2.6, which

One way to compute the dispersion numerically is to obtain the set of values of γ a and, hence, the

energies that satisfy the ±1 restriction, as shown in Figure 2.5. This set of values organizes in