Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

2.6 Insights from the Kronig–Penney model 29

2π

3π

4π

–1

cos

sin

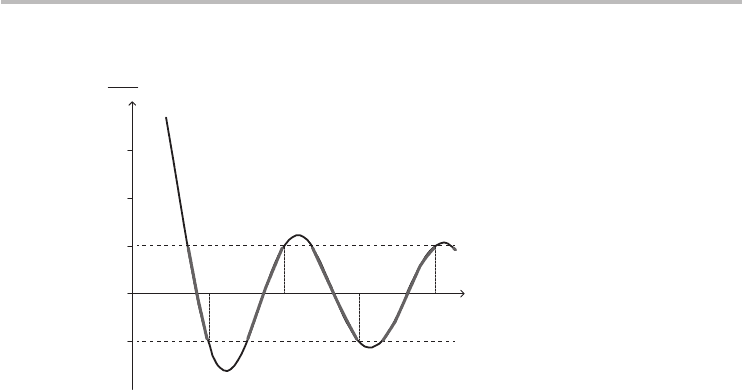
Fig.2.5GraphoftheRHSofEq.(2.25).Thegraylinesbetween±1dashedlinesaretheallowed

solutions. Only the positive γ a is shown here; the negative γ a is the mirror image.

clearly reveals a set of allowed energy bands separated by bandgaps. For com-

parison, the dispersion of a free electron in space has also been included in the

ﬁgure.

2.6 Important insights from the Kronig–Penney model

It is worthwhile taking this opportunity to explain the other key features of the

dispersion in Figure 2.6, beyond the discussion of allowed bands separated by

bandgaps.

→ Brillouin Zone: Eq. (2.25) does not have a unique solution. For every

allowed energy that yields an LHS value within ±1 there will be correspondingly

an inﬁnite set of wavevectors k. For example, let us say a speciﬁc energy value

leads to an LHS of +1. As a result, the wavevector calculated from cos ka =+1

yields inﬁnite acceptable k-values due to the repeating nature of the trigonometric

functions. It is often convenient to obtain a ﬁnite and unique (non-repeating) set

of allowed E−k pairs. To achieve this, we consider wavevectors within a single

period of the LHS. Additionally, we chose this period to be symmetric around

the origin, i.e. ka =[−π, +π]. The space or zone restricted to these k-values is

formally called the ﬁrst Brillouin zone and is illustrated as the shaded region in

Figure 2.6. Similarly, for every allowed wavevector there are inﬁnite allowed ener-

gies, corresponding to one allowed energy per band, for a total of inﬁnite bands.

To see this visually, consider cos ka = 0, which corresponds to the horizontal

bands demarcated by γ a = π. For example, the energies of the nth band satisfy the restriction

lieing within γ a =[(n −1)π , nπ ]. Once the energies are known, the wavevector is computed from

Eq. (2.25).

30 Chapter 2 Electrons in solids: a basic introduction

2ππ 3π–3π –2π –π

Band 1

Band 2

Band 3

Bandgap

Fig. 2.6 The dispersion of an electron in the Kronig–Penney model showing allowed bands

separated by bandgaps. The dashed curve is the dispersion of a free electron.

intersection of the curve passing through the origin (Figure 2.5). Owing to the

oscillatory nature of the curve resulting from cos γ a in Eq. (2.25) there will be an

inﬁnite number of allowed energies for that given k-value. However, there are a

ﬁnite number of electrons in any solid, and we will discover throughout this book

(seeChapters3and4forexample)thatourfocuswillbeonthepropertiesofthe

highest energy electrons which are largely responsible for the device physics. How

the highest energies of relevance are determined will be elucidated with the idea

oftheFermienergydiscussedinChapter3.

→ Nearly-free Electron: In the limit that P → 0, then k → λ (see Eq. (2.25))

and we recover the dispersion for an electron in an empty solid of size L:

E =



2mL

, n =±1, ±2, ±3, ... (2.26)

This informs us that, in the limit of a weak periodic potential, the electron would

increasingly behave as if it were nearly free; that is, it can move around in the

solid with negligible or no impediment from the periodic potential.

Indeed, there

is a widely used model in solid-state physics called the nearly-free electron model

that assumes the electron behaves like a free electron but it only slightly perturbed

by the periodic potential, which is essentially accounted for (to ﬁrst order) as a

This can be considered the most accurate description of what we mean by a “free (or nearly-free)

electron” model.

2.6 Insights from the Kronig–Penney model 31

constant potential in the Schrödinger equation (Eq. (2.1)). The nearly free electron

model is particularly useful in predicting fairly accurate band structures of bulk

metals and the existence (or lack thereof) of bandgaps in crystalline solids.

→ Tightly Bound Electron: In the opposite limit, when P →∞, then the

solutions to Eq. (2.25) exist only when γ a = nπ , and the dispersion becomes

E =



2ma

, n =±1, ±2, ±3, ..., (2.27)

which at ﬁrst glance appears similar to Eq. (2.26) with the important difference

that Eq. (2.27) corresponds to the case of an electron moving within a space of

size a. This is interpreted as an electron trapped or localized within the inﬁnite

potential walls; as a result, it is not free to move around the entire solid of size

L, in contrast to the nearly-free electron case. This informs us that, in the limit of

an increasingly strong periodic potential, the electron behaves as if it were tightly

bound by the strong potential, which in reality represents the attraction from the

atomic nucleus. The case of a strong periodic potential is of signiﬁcant practical

interest and is formally treated by methods such as the tight-binding model. In fact,

this is the most widely used model for accurately describing the band structure of

graphene and carbon nanotubes. This model will be discussed in more detail in

the derivation of the band structure of graphene.

→Parabolic-like Dispersions: We learned fromthe Kronig–Penney model that

the dispersion is fairly parabolic in structure, particularly at the bottom or top of

each band (see Figure 2.6). While we utilized a delta periodic potential in the spe-

ciﬁc model, the qualitative features of the band structure are fairly insensitive to the

speciﬁc form of theperiodic potential.Acase inpoint is a repeating squarepotential

which also yields a parabolic-like band structure. To a great degree, many (but not

all) solids, including metals and semiconductors, exhibit parabolic-like dispersions

at the bottom and top of their bands of interest. As a result, there has been great

intellectual activity in developing simple algebraic equations based on modiﬁca-

tions of the free-electron parabola to describe the dispersion (and resulting device

physics) of solids, particularly semiconductors, with varying degrees of accuracy.

The algebraic expression generally takes one of the following analytical forms:

E ≈



eff

(2.28)

E(1 + αE) ≈



eff

, (2.29)

where m

eff

represents the effective mass of electrons speciﬁc to the particular

solid and conceptually embodies the effect of the periodic potential on the motion

or mobility of the electrons in the solid. The non-parabolicity parameter α quan-

tiﬁes how the actual dispersion of interest compares with an ideal free-electron

parabola and is (approximately) inversely proportional to the bandgap. These three

32 Chapter 2 Electrons in solids: a basic introduction

parameters are often determined in practice by ﬁtting the algebraic equation to

experimental data or extracted directly from ab-initio

computation.

We have discussed the Kronig–Penney model of electrons in a periodic potential

quite extensively; on the other hand, we have yet to address why bandgaps exist

in the ﬁrst place. It is not at all instantly obvious why bandgaps should exist.

However, when we view the electrons strictly as waves, then wave principles,

such as reﬂections, are applicable. It is the reﬂections of electron waves from the

potential wall that lead to bandgaps. And, analogous to electromagnetic waves,

these reﬂections are an integral multiple of wavelength, and that is why we observe

the bandgaps occurring at kα =±nπ. In solid-state physics, these reﬂections are

called Bragg reﬂections.

2.7 Basic crystal structure of solids

In the previous section we gained much insight into how electrons behave in a

crystalline solid (a solid with a periodic potential). The Kronig–Penney model, for

instance, is not only of great educational value, but its dispersion is often also used

to ﬁt the actual dispersion of many bulk solids. Nonetheless, the Kronig–Penney

model is inherently limited because it is a general model that does not take into

account the speciﬁc lattice arrangement of a particular solid of interest. For exam-

ple, if we desire to determine the band structure of nanotubes and nanoribbons, the

Kronig–Penney model is utterly inadequate in providing basic information such

as the bandgap dependency on the diameter of these nanostructures.

In order to make any further progress in determining the speciﬁc band structure

of a particular solid, we would need to understand the crystal structure of that

particular solid. To underscore the importance of the crystal structure, it would

be fair to state that it is at the core of modern solid-state physics. The crystal

structure can be viewed in two domains similar to how a coin has two views. One

domain is in position (sometimes called direct) space and the other domain is in

reciprocal space. We will start by discussing the lattice arrangement in position

space, subsequently followed by a corresponding discussion in reciprocal space.

Our focus here will be on discussion of the crystal structure that is relevant to this

text, namely for the development of two-dimensional (2D) or reduced-dimensional

solids (graphene and CNTs). As such, the spotlight will be on lattices in 2D space.

For a more general coverage of crystal structures, the reader will ﬁnd a general

solid-state textbook very informative.

Ab initio is a Latin term that means from ﬁrst principles or from the beginning. In science, it refers

to a thorough calculation that starts directly from accepted laws (such as Schrondinger’s equation)

and does not use empirical data or ﬁtting in the calculation.

For an introductory graduate-level coverage see C. Kittel, Introduction to Solid State Physics, 8th

edition (Wiley, 2004). For more advanced studies, consider the classic text N. W. Ashcroft and

N. D. Mermin, Solid State Physics (Brooks/Cole, 1976).

2.8 The Bravais lattice 33

(a)

(b)

Fig. 2.7

(a) Macroscopic image of a “round brilliant cut” diamond (courtesy europeanj.com).

(b) High-resolution TEM image of the crystal lattice of diamond. Inter-atomic distance is

∼2–2.1 Å. Copyright (1990) Materials Research Society. Courtesy of B.E. Williams,

H.S. Kong, and J.T. Glass, J. Mater. Res., 5 (1990) 801.

Figure 2.7a shows the macroscopic appearance of a diamond crystal with its

visible symmetric crystal planes. However, the physical glamour of a solid is not a

sufﬁcient measure for crystallinity. What is required is microscopic periodicity of

the lattice. Figure 2.7b is a high-resolution TEM image of a region in a diamond

crystal with noticeable periodicity, where each bright spot represents a carbon

atom. Our concern will be on the characteristic underlying microscopic lattice of

the crystal structure. As such, a systematic mathematical formalism is needed to

describe the geometry of the lattice. From this mathematical formalism we can

then develop a technique to compute the band structure of particular solids. To

foreshadow the discussion to come, it is worthwhile stating in advance the logical

relation which is the foundation of crystal structure,

Crystal Lattice = Bravais Lattice + Basis

where Bravais lattice is the technical name for the fundamental irreducible micro-

scopic arrangement of points and the basis is an integer number that represents

how many atoms are attached to each Bravais lattice point.

2.8 The Bravais lattice

There are several ways to describe a lattice. The most fundamental description is

known as the Bravais

lattice. In words, a Bravais lattice is an array of discrete

points with an arrangement and orientation that look exactly the same from any of

the discrete points; that is, the lattice points are indistinguishable from one another.

The Bravais lattice point itself represents some “stuff,” where “stuff” could be a

single atom, a collection of atoms, molecules, and so on and so forth. The amount

Named after the French physicist Auguste Bravais who correctly pointed out in the mid 1800s that

there are 14 unique fundamental lattices in 3D space, revising the earlier calculation of 15 lattices

by Frankenheim, otherwise they would be known as Frankenheim lattices today.

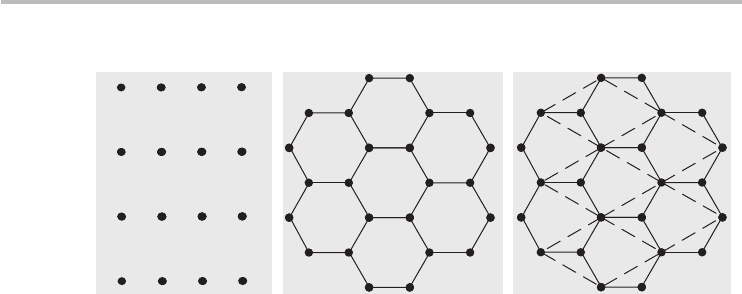
34 Chapter 2 Electrons in solids: a basic introduction

(a) (b) (c)

Fig. 2.8

(a) A rectangular lattice qualiﬁes as a Bravais lattice. (b) A honeycomb lattice is not a

Bravais lattice. (c) Conversion of the honeycomb into a Bravais lattice with a basis of 2.

The underlying Bravais lattice is represented by dashed lines.

of “stuff” at each Bravais lattice point is what we earlier called the basis. It is

signiﬁcantly easier to grasp the meaning of a Bravais lattice and basis visually.

Let us consider the lattices shown in Figure 2.8. Every discrete point in the 2D

rectangular lattice sees exactly the same environment. Imagine placing a camera

at one of the discrete points and taking a picture to the right of the point. That

picture will look exactly the same if it were taken from any other discrete point in

the lattice. As a result, the rectangular lattice is a Bravais lattice and has a basis of

one. That is, every Bravais lattice point represents a single crystal lattice point.

Let us perform the same thought experiment with the camera on the honey-

comb lattice in Figure 2.8b. Let us say that initially the camera is at point A and

the image is taking facing rightwards. If we move the camera to point B fac-

ing rightwards, then the resulting image from B is obviously not the same as the

image from A. For one, point A is directly looking at a single lattice point, while

point B faces two lattice points at angles of ±60

◦

. Consequently, the honeycomb,

as it is, is not a Bravais or fundamental lattice. However, the honeycomb crys-

tal is still a lattice because it consists of repeating unit cells and, as a result, it

can be converted or mapped to a Bravais lattice. The process of converting a

non-fundamental lattice to a Bravais lattice occurs most conveniently by liter-

ally staring at the lattice (long enough) to identify a collection of crystal lattice

points that when grouped together will result in a Bravais lattice. For the partic-

ular example of a honeycomb, consider grouping points A and B together (and

all repeating instances of A and B); the resulting lattice is shown in Figure 2.8c,

which is now a Bravais lattice, and has a basis of two. That is, every Bravais lattice

point represents two crystal lattice points. In crystalline solids, the real points are

locations of atoms and the basis is conveniently interpreted as the number of atoms

grouped together at each Bravais lattice point. It is important to keep in mind that

the Bravais lattice is not always the same as the crystal lattice, as this example

demonstrates.

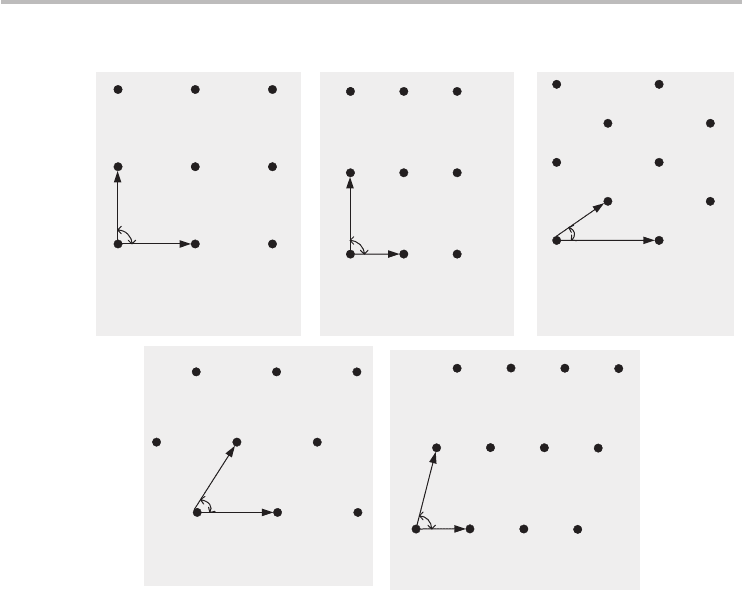
2.8 The Bravais lattice 35

Square lattice

|=|a

|, f=90°

Rectangular lattice

|=|a

|, f=90°

Centered

rectangular lattice

|=|a

|, f=90°

Hexagonal lattice

|=|a

|, f=60°

Oblique lattice

|=|a

|, f=60°

Fig. 2.9

The ﬁve unique Bravais lattices in 2D space.

There are precisely ﬁve Bravais lattices in 2D space (Figure 2.9) and 14 Bravais

lattices in 3D space. These precise totals are determined from symmetry properties

of Bravais lattice points. For instance, the square lattice is invariant under rotation

of 90

◦

about a ﬁxed lattice point in 2D space. The hexagonal lattice, on the other

hand, is invariant under rotation of 60

◦

. By carefully taking into account the rotation

symmetry, and symmetry present in lattice spacing, the Bravais lattices can be

fully enumerated. The mastery of all the details of crystallographic symmetry

is (fortunately) not necessary for an advanced working knowledge of crystalline

solids.

A useful property of crystal lattices which we will later employ in the derivation

of electronic band structures is the nearest neighbors. The nearest neighbors are the

number of points that are equally closest to a given point in the Bravais lattice. For

example, the nearest neighbors are two and four for any point in the rectangular

and square lattices respectively (see Figure 2.9).

There is a tremendous amount of sophisticated detail formulated in the language of group theory,

which is a discipline within abstract algebra. Further reading on group theory can be found in the

references in footnote 6.

36 Chapter 2 Electrons in solids: a basic introduction

Primitive vectors

In order to describe the position of Bravais lattice points, we need to deﬁne a

coordinate origin and vectors (a

and a

in 2D space). Any integral multiple of

these vectors must arrive at a Bravais lattice point, i.e. the position vectors (also

known as the Bravais lattice vectors) of any lattice point is R = n

+ n

where n

and n

are positive or negative integers. To state it in a different manner,

the entire Bravais lattice can be constructed by translating the coordinate vectors

in integral steps throughout space. These coordinate vectors associated with the

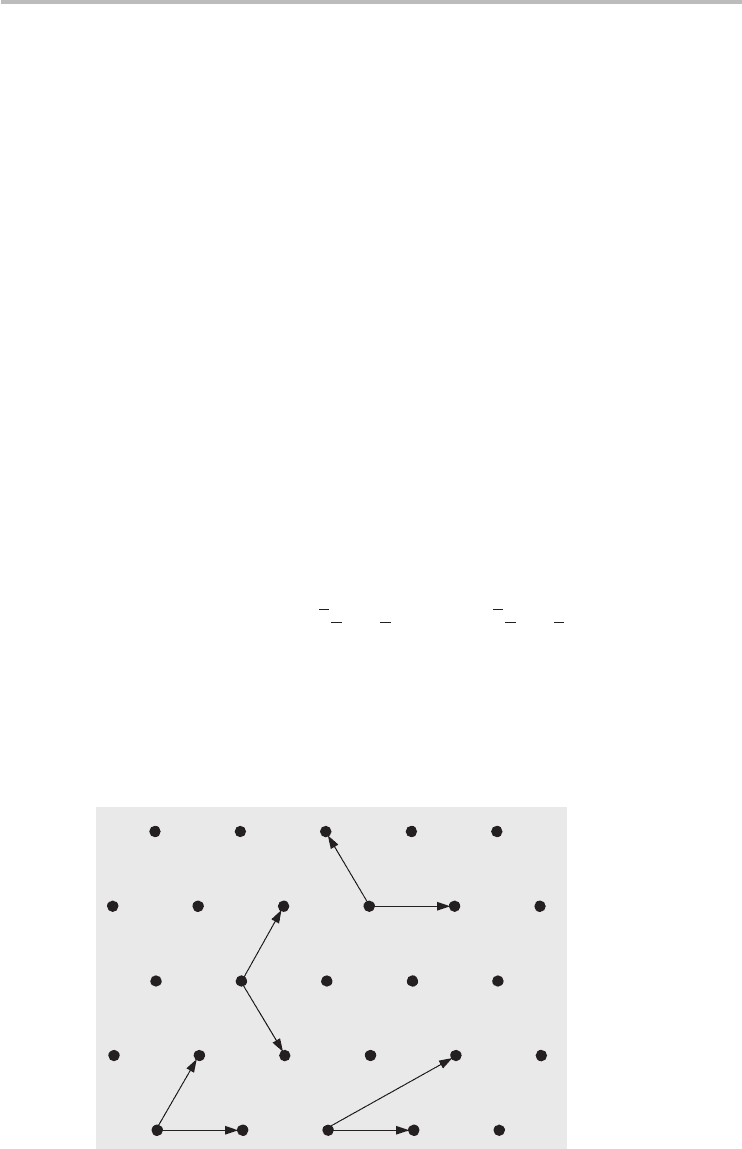
Bravais lattice are called the primitive vectors. Figure 2.10 illustrates four choices

of primitive vectors (a

and a

) for the hexagonal lattice, evidently conveying

that the pairs of primitive vectors are not unique. In practice, a symmetrical or

geometrically convenient pair of primitive vectors is often chosen for simplicity.

We all learn better from examples, so let us go through an example to locate

point Q in Figure 2.11. After ﬁrst verifying it is a Bravais lattice, we then deﬁne a

reference point which will serve as the origin for the Cartesian coordinate system

and, for convenience, also the origin for the primitive unit vectors (the light gray

lattice point in the ﬁgure). Second, we deﬁne the primitive vectors in terms of

the Cartesian coordinates. In this case, we chose a symmetrical set of primitive

vectors.

√

ˆx +

ˆy, a

√

ˆx −

ˆy, (2.30)

where a is the lattice constant, and for the hexagonal lattice a =|a

|=|a

Finally, it is a simple matter to locate point Q by traveling two primitive vectors

in the negative a

direction and one primitive vector in a

(the dashed arrow lines

in the ﬁgure). The Bravais lattice vector for point Q is R = a

–2a

Fig. 2.10 Hexagonal Bravais lattice with several choices for pairs of primitive vectors.

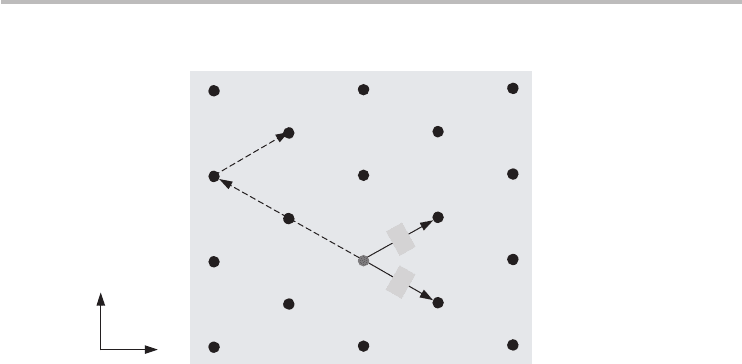
2.8 The Bravais lattice 37

–2a

Fig. 2.11 An example using primitive vectors to determine the location of point Q in the lattice.

Primitive unit cell

The most basic unit cell of the Bravais lattice is called the primitive unit cell. The

primitive unit cell has two distinguishing properties: (1) it is a region of space

that contains exactly one Bravais lattice point; (2) it recreates the lattice when

translated through all the Bravais lattice vectors without leaving gaps or generating

overlaps. From the former property, the density of points in the primitive unit cell

is one point/volume, where volume refers to the volume of the primitive cell. An

additional observation from the former property is that the actual number of crystal

lattice points contained in the primitive unit cell is equal to the basis. Similar to

the primitive vectors, there is no unique way of choosing a primitive unit cell for

a given Bravais lattice. Fortunately, in 2D space this is a relatively trivial matter,

as it is easy to identify a primitive unit cell for any of the ﬁve Bravais lattices by

visual inspection. Figure 2.12a illustrates some examples of primitive unit cells for

the square lattice. All primitive unit cells occupy exactly the same area or volume.

In three dimensions, it can become painfully difﬁcult to visualize and sketch

Bravais lattices,

let alone construct a 3D primitive unit cell. To overcome this,

a primitive unit cell known as the Wigner–Seitz cell has become broadly utilized,

andisconstructedfromstraightforwardgeometricalrules.

TheWigner–Seitz

cell is especially very valuable in understanding the properties of the reciprocal

lattice and the band structure which will be developed in the subsequent section

and chapter.

Formally, the Wigner–Seitz cell is a primitive unit cell that has a

boundary about a Bravais lattice point that contains only that lattice point. That

boundary is closest to that lattice point than to any other lattice point. What does

This is particularly true for the non-artists. More often than not, students who have a talent for

sketching ﬁnd themselves excelling in solid-state physics (at least in the areas of crystallography)

compared with their artistically challenged peers.

This is the primary incentive to learn the construction of the Wigner–Seitz cell in 2D space.

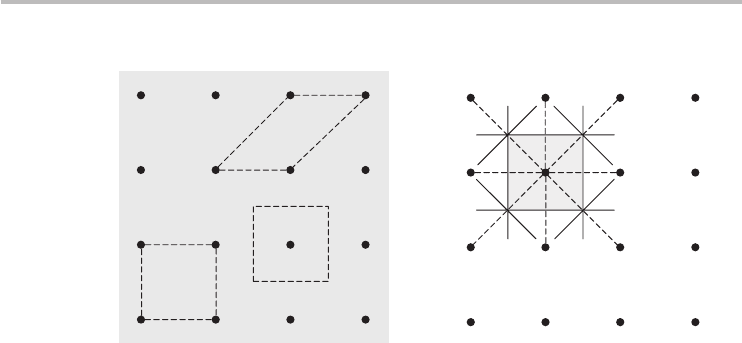
38 Chapter 2 Electrons in solids: a basic introduction

(a)

(b)

Fig. 2.12 Square lattice. (a) Several choices of primitive unit cells. (b) Construction of the

Wigner–Seitz cell (gray square).

that really mean? We ﬁnd again that a picture is often more informative than many

words. The Wigner–Seitz cell for the square lattice is shown in Figure 2.12b. The

cell is constructed from the following recipe:

•

Draw a connection line linking the lattice point to adjacent lattice points, often

up to the second nearest neighbors. The connection lines are dashed lines in

Figure 2.12b.

•

Bisect the connection lines with perpendicular lines (solid lines in Figure 2.12b).

•

Connect the bisecting lines at common intersections to form a closed polygon

(shaded region in Figure 2.12b).

While the ensuing square Wigner–Seitz cell for the square lattice appears fairly

uninteresting, the inquisitive reader will ﬁnd it enlightening and even enjoyable to

construct the Wigner–Seitz cell for the other 2D Bravais lattices. In those cases,

the Wigner–Seitz cell is always a hexagon except for the rectangular lattice. The

Wigner–Seitz cell exhibits the symmetry of the corresponding Bravais lattice; for

example, the rotational symmetry is invariant. To keep the focus on the main

subject of this text (2D solid matter), we will not discuss 3D Wigner–Seitz cells,

which can have very complex structures. Needless to say, such discussion can be

readily found in any standard texts on solid-state physics.

In this section, we have learned about four concepts which are important for

obtaining a working knowledge of crystalline solids. These concepts are Bravais

lattice, lattice basis, primitive unit vectors, and the primitive unit cell or Wigner–

Seitz cell.

2.9 The reciprocal lattice

In the prior section we elaborated on the crystal lattice. In general, it is composed

of a Bravais lattice and a basis. The Bravais lattice, which is normally measured