Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

4.11 Problem set 99

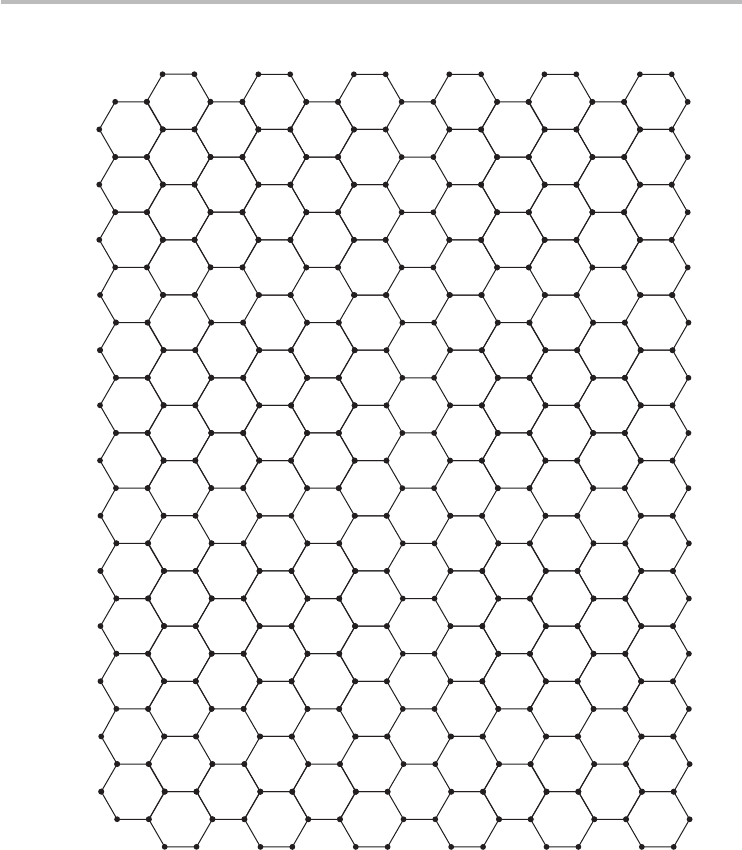
Fig. 4.14 The honeycomb lattice of graphene.

the ﬁrst Brillouin zone? (Hint: a shortcut to the answer is available by

inspection of the Brillouin zone.)

4.2. Construction of a (5, 5) CNT.

Redo Problems 4.1 for a (5, 5) CNT.

4.3. Starting from Eq. (4.11), derive the expressions for K

and K

as shown in

Eqs. (4.14) and (4.15).

4.4. Chiral index convention.

By convention, the geometric description of CNTs is restricted to chiral

indices from (n,0)to(n, m), where n and m are integers and m ≤ n. The

100 Chapter 4 Carbon nanotubes

immediate question then is: Why is m > n not considered interesting? To

address this question, show that an (n, n +p) CNT is identical to an (n +p, n)

CNT where p is a positive integer.

4.5. Carbon nanotube subband degeneracies.

Accurately keeping track of the CNT subband degeneracies (subbands with

identical E − k relation) is routinely necessary even for the most basic nan-

otube analysis. While tracking degeneracies should be somewhat trivial, it

is quite common for new readers to be puzzled by a factor of two (or more)

every now and then. The purpose of this exercise is to give the reader some

familiarity with the degeneraciesthat occur,particularly at thehigh-symmetry

points of the nanotube band structure.

(a) What are the band degeneracies for the CNTsubband that is at the -point

and K-point of the Brillouin zone of graphene? That is, a subband that

touches these symmetry points. Determine an answer by direct analysis

from the Brillouin zone of graphene for armchair and zigzag nanotubes.

(b) Likewise, what are the band degeneracies for the CNT subband in the

interior of the Brillouin zone of graphene? Determine an answer by direct

analysis from the Brillouin zone of graphene for armchair and zigzag

chiral nanotubes.

The emphasis on the direct analysis of the Brillouin zone of graphene is

because this is the fastest and easiest way to determine nanotube subband

degeneracies.

4.6. Carbon nanotube second lowest subband.

In the modeling of electron transport in CNTs, it is generally desirable to

include contributions to current from the lowest and higher subbands. In many

(but not all) cases, only the two lowest subbands will effectively determine

charge transport. Therefore, an accurate analytical expression for the band

index and energy minima of the second subband will be most welcome.

Consider a semiconducting zigzag nanotube.

(a) Derive an approximate analytical expression for the second subband

index and the subband energy minima.

(b) Determine the accuracy of the energy minima from part (a) by comparing

with the tight-binding predictions for zigzag nanotubes with diameters

from 1 to 3 nm.

the ﬁrst subband and the second subband?

4.7. Robustness of random distribution of the metallic/semiconducting character

of nanotubes.

It is commonly known and shown in thetext that a random distribution oflarge

numbers of CNTs will reveal that one-third are metallic and the remaining

4.11 Problem set 101

two-third semiconducting. However, one cannot help but wonder if this is

also the case for a limited sample of CNTs. Show that the 1/3 ratio is fairly

robust even for a limited range of random chiralities. For example, in practice,

grown CNTs are usually within the 0.7 to 2 nm range. Let us say we examine

chiral indices from (8, 0) to (30, 0) combinations to represent the range of

diameters of interest.

(a) What is the probability of metallic and semiconducting nanotubes within

this range of chiral indices? Quantify the departure (if any, in percent)

from the 1/3, 2/3 probabilities expected for large numbers of nanotubes.

(b) Imagine there was a method to produce only chiral nanotubes. What will

be the resulting probabilities of metallic and semiconducting CNTs?

4.8. Probability of zigzag CNTs.

Zigzag CNTs are usually easier to model and analyze owing to their high-

symmetry structure that affords simpler closed-form mathematics. In many

cases, the general properties of semiconducting CNTs are then inferred by

analyzing a semiconducting zigzag nanotube of comparable diameter.

(a) One question of intellectual curiosity then arises: What is the probability

that a CNT is a semiconducting zigzag CNT from a random distribution

of a large number of carbon nanotubes?

(b) Compare the probability of a semiconducting zigzag nanotube with that

of the 2/3 expected for an arbitrary semiconducting nanotube. Which

type of nanotube (zigzag or chiral) makes up the lion’s share of the 2/3

probability of semiconducting nanotubes?

is the probability of metallic and semiconducting zigzag nanotubes in the

ensemble?

4.9. From nanotubes to nanoribbons.

It has recently been shown that GNRs can be produced by unzipping CNTs

along the longitudinal direction.

(a) What type of GNR is expected if a zigzag nanotube is unzipped?

(b) What type of GNR is expected if an armchair nanotube is unzipped?

5 Carbon nanotube equilibrium

properties

5.1 Introduction

This chapter explores the equilibrium and thermodynamic electronic proper-

ties of single-wall CNTs. Equilibrium refers to the state of a system in the

absence of external forces, and thermodynamics accounts for the evolution of

the macroscopic properties of the system with temperature. The system we are

referring to here is of course CNTs, and the properties of interest include the

DOS, group velocity, effective mass, and charge carrier density. These prop-

erties are of central importance for understanding and predicting the electrical,

optical, and thermal behavior of CNTs. Our learning path will utilize the devel-

opment of analytical expressions of these properties to provide insight and

understanding regarding the inherent solid-state behavior. Additionally, analyt-

ical expressions are especially desirable for compact modeling of nanotube

devices.

In order to be comfortable with the discussion of the equilibrium properties,

the reader should be familiar with the band structure of CNTs developed in the

previous chapter. In fact, it will be worthwhile to have in hand a copy of all

thebandstructureﬁguresshowninChapter4asonegoesthroughthischapter.

The equilibrium properties will be employed repeatedly in subsequent chapters

to describe transport in CNTs under the quasi-equilibrium assumption applica-

ble at low energies. We begin by discussing the DOS of the free-electron gas

in 1D space. This provides perspective, allowing us to appreciate and relate to

the actual DOS in CNTs which are quasi-1D solids. In general, the DOS is of

fundamental importance in understanding crystalline solids, and many of the

other equilibrium properties can be derived from this important parameter. We

conclude the chapter by deriving the electron and hole carrier densities at ﬁnite

temperatures.

5.2 Free-electron density of states in one dimension 103

5.2 Free-electron density of states in one dimension

The DOS is a fundamental property of solids that describes the number of states

available to be occupied by a particle at every allowed energy. The particles could

be elementary wave-like particles, such as electrons, holes, photons, and phonons,

or composite wave-like entities, such as excitons (electron–hole pairs). The parti-

cles of primary interest to us are electrons and holes. In a casual sense a state is

akin to a home; and just like a home can house say one or two persons, a state

can also accommodate one or two particles. In the same sense, the DOS in a solid

is analogous to the density of homes in a city. It follows, then, that the number

of particles present in a solid can be calculated in a straightforward manner by

estimating the number of states that are occupied. Mathematically, the DOS g(E)

(where E is the particle energy) for a 1D solid can be interpreted based on the form

that it is presented, such as

g(E) ⇒ DOS per unit length at energy E,

g(E) dE ⇒ total number of states per unit length between E and E +dE,



g(E) dE ⇒ total number of states per unit length between E

and E

Every allowed state is associated with two parameters: the wavevector k and the

corresponding energy.

It is worthwhile examining the free-electron DOS in 1D space in order to obtain

insight about the general formalism of deriving and interpreting the features of

theelectronDOS.WerecallfromChapter2thattheenergydispersionofthe

free-electron gas can be expressed as

E =



+ E

, (5.1)

where m is the electron mass,  is the reduced Planck’s constant, and E

is the

energy at the bottom of the parabolic band, which can be interpreted as the potential

energy, and E −E

represents the electron kinetic energy. In a 1D solid, the number

of states between E and E + dE is the differential wave vector dk normalized to

the length of one state:

g(E) dEL= 2

2π/L

, (5.2)

where L is the length of the 1D system and 2π/L is the length of one k-state; the

factor of 2 in the numerator accounts for spin degeneracy. Hence, it follows that a

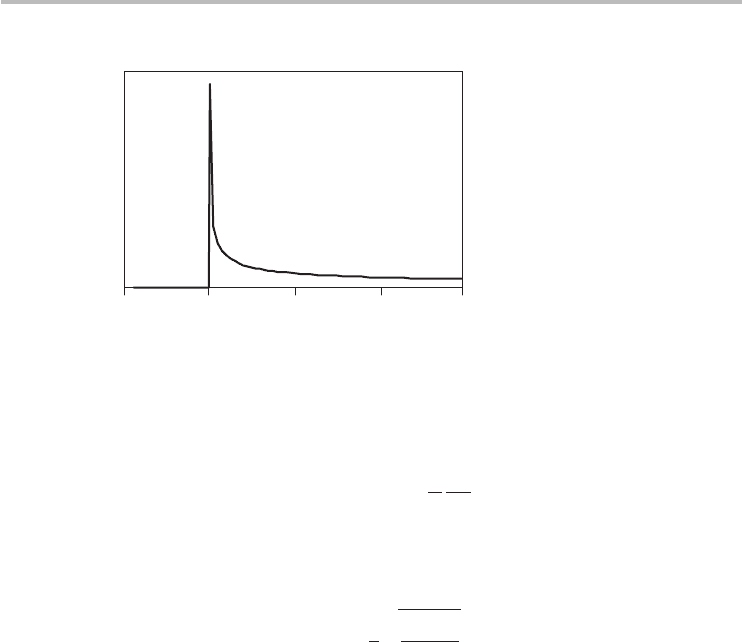
104 Chapter 5 Carbon nanotube equilibrium properties

01234

g(E) arb. units

E/E

Fig. 5.1 The DOS of free electrons in a 1D solid.

general formula for the electron DOS in a 1D solid is

g(E) =

. (5.3)

Applying the formula to Eq. (5.1) allows us to derive the DOS of free electrons in

a 1D solid:

g(E) =













E − E

E > E

0 E ≤ E

, (5.4)

which is shown graphically in Figure 5.1.

There are several insights we gain visually from the free-electron DOS in 1D,

including:

(i) There are no states inside the bandgap (E < E

), a general truth applicable

to all ideal crystalline solids.

(ii) There are no states at E = E

, which, although it might not be obvious, can

be deduced from fundamental postulates in quantum mechanics. In quantum

mechanics, electrons are only allowedto exist instates that havea positive and

ﬁnite kinetic energy (E −E

> 0) leading to moving states. If states existed

at E = E

, the electrons in those states would be stationary,

implying that

we can determine their position precisely, which would violate Heisenberg’s

uncertainty principle. Although the DOS diverges as E → E

, it is actually

never inﬁnite because E = E

is not an allowed energy. The divergence

of the DOS is also known as a van Hove singularity (VHS), and hence E

The velocity of an electron is formally related to the DOS in Section 5.6 where we ﬁnd that E = E

corresponds to states with zero velocity for parabolic-like dispersions.

5.3 Density of states of zigzag nanotubes 105

corresponds to the energy of the singularity. Van Hove singularities are key

features of the electron DOS of 1D solids with a parabolic-like dispersion.

(iii) For E > E

, the DOS g(E) ∼ 1/

√

E − E

, another key characteristic of 1D

crystalline solids with parabolic-like dispersion.

In summary, there are two key features of the DOS which are particular to

1D solids in the limit of free electrons: VHS and the DOS inverse square-root

dependence on energy. Interestingly, these two features are present in the DOS of

electrons and holes in CNTs; as such, a CNT can be considered a 1D solid.

5.3 Density of states of zigzag nanotubes

The CNT electronic structure has many 1D subbands; as such, the total DOS g

tot

at a given energy is the sum of the contributions from the DOS of each subband.

Consider an inﬁnitely long CNT for mathematical ease:

the total DOS and the

DOS per subband are respectively

tot

(E) =



j=1

g(E, j) (5.5)

and

g(E, j) =



∂E

∂k



−1



∂k

∂E



, (5.6)

where N is the number of subbands in the CNT band structure.

For simplicity, we shall ﬁrst derive the DOS for zigzag (n,0) nanotubes, then

armchair (n, n) nanotubes, and ﬁnally arbitrary chiral (n, m) nanotubes. The E−k

dispersion of zigzag nanotubes is

E(k, j) =±γ







1 + 4 cos



√

3ka



cos



πj



+ 4 cos



πj



, (5.7)

where j is the subband integer index, which ranges from 1 to 2n, a is the graphene

Bravais lattice constant (∼2.46 Å), and γ is the nearest neighbor overlap energy and

nominally ∼3.1 eV. The positive and negative preﬁxes refer to the band structures

of the conduction (π

∗

) and valence (π) bands respectively. The intrinsic Fermi

energy is 0 eV. To derive the DOS for zigzag CNTs g

, it is more convenient to

Recall from Section 4.4 that an inﬁnitely long CNT allows us to employ continuum mathematics

for k-values in the axial direction, which remains a good approximation for nanotubes as short as

10 nm.

106 Chapter 5 Carbon nanotube equilibrium properties

evaluate the RHS of Eq. (5.6), because ∂k/∂E results in an expression which is

an explicit function of E. The wavevector for a zigzag CNT is

k =±

√

cos

−1



sec



πj



− 2 cos



2πj



− 3



. (5.8)

For deriving the DOS, it is easiest to differentiate the positive branch of the

wavevector with respect to energy according to Eq. (5.6). It follows that, by orga-

nizing the resulting denominator, the DOS due to positive wavevectors can be

written in the form given by

(E, j) =

√

3aπ

|E|



− E

)(E

− E

)

(5.9)

for C

≤ E ≤ C

for the conduction band and V

≤ E ≤ V

for the valence band.

and C

are the bottom and top of the conduction band respectively, and V

and

are the bottom and top of the valence band respectively. The notation C

and

will refer to the bottom and top of the ith subband respectively, and vice versa

for the valence band (see Figure 5.2).

vh1

and E

vh2

(the roots of the denominator)

are the energies of the VHS in zigzag nanotubes and deﬁne the energy space where

the DOS is real. Owing to mirror symmetry of the E−k relationship, the DOS for

the negative branch of the wavevector is identical to g

. Hence, the complete DOS

from both branches of the wavevector for the jth subband is

(E, j) =

4α

√

3απ

|E|



− E

vh1

)(E

vh2

− E

)

. (5.10)

Here, α accounts for the Brillouin zone mirror symmetry or degeneracy.

Specif-

ically, α = 1ifE is energy at the Brillouin zone center (since the -point center

is common to both branches of the wavevector), otherwise α = 2. The Brillouin

zone is illustrated in Figure 5.2. Moreover, the distinction in α is only relevant to

the ﬁrst subband of metallic nanotubes because they possess moving states at the

-point. Practically speaking, for semiconducting zigzag CNTs (or subbands with

parabolic-like curvature), α is always 2, since no states are allowed at the -point

because of the zero velocity, which violates the uncertainty principle.

Electro-optical applications of CNTs mostly involve C

and V

, with little concern for C

and V

which are at higher energies.

Keeping track of all the degeneracies or symmetries present when calculating the properties of

nanotubes can quite easily tax the brain, and sometimes lead to a factor of 2 dilemma. The family of

degeneracies includes spin degeneracy, subband degeneracy, point degeneracy at the Fermi energy,

and Brillouin zone mirror symmetry (α). The key to becoming comfortable with degeneracies is to

personally rederive the equilibrium properties such as the DOS from the band structure.

5.3 Density of states of zigzag nanotubes 107

k (wavevector)

E (eV)

–4

–2

Fig. 5.2 Illustrative band structure of a nanotube displaying only the positive half of the Brillouin

zone, and identifying the symmetry points  (center of BZ) and X (end of BZ). This

particular case is for a (13, 0) CNT including only two subbands of the valence and

conduction bands, and graphically indicating C

, C

, V

, and V

It is now timely to formally introduce the formulas of all the energy parameters

deﬁned so far in this section. The VHS are given by

vh1

(j) =±γ



1 + 2 cos



jπ





, (5.11)

vh2

(j) =±γ



1 − 2 cos



jπ





. (5.12)

We observe that the energies of the VHSs are chirality dependent and periodic with

period 2n, which is because there are identically 2n unique 1D subbands in the

zigzag CNT Brillouin zone. E

vh1

is located at the -point and E

vh2

is in the second

Brillouin zone. These two singularities generally reﬂect the two minima/maxima

present in a periodic sinusoid. In the case of a nanotube, it is the quasi-sinusoidal

energy dispersion that leads to the VHS. The all-important bandgap is directly

determined from E

vh1

of the ﬁrst subband. Let us call the subband index for the

ﬁrst subband j

, then the bandgap is

= 2C

= 2E

) = 2γ



1 + 2 cos



πj





. (5.13)

The ﬁrst subband index was determined in Chapter 4 to be j

= round(2n/3),

where round is a function that converts its argument to the nearest integer. A

simpler approximation (useful to memorize) relating the bandgap and diameter

explicitly was also derived in Chapter 4 to be

= 2γ

√

= 2γ

C−C

, (5.14)

where a

C−C

is the carbon–carbon bond length (∼1.42 Å).

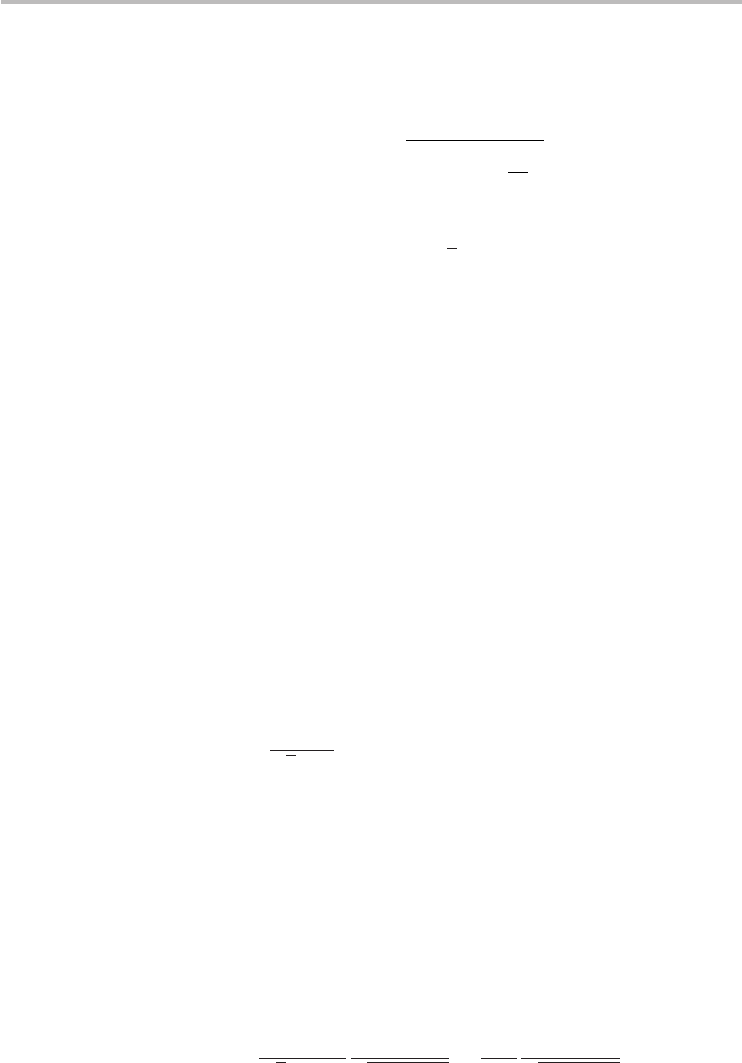
108 Chapter 5 Carbon nanotube equilibrium properties

In order to deduce an equation for the bottom and top of the bands, another

energy deﬁnition is required for completeness:

(j) =±γ



1 + 4 cos



πj



. (5.15)

is the energy at the boundary of the ﬁrst Brillouin zone (X-point in Figure 5.2),

which is calculated by plugging k = π/

√

3a into Eq. (5.7). Depending on the

subband, the bottom or top of the subband is either at the -point or at the X-point.

Therefore:

= min(E

vh1

, E

) =−V

, (5.16)

= max(E

vh1

, E

) =−V

, (5.17)

where min( ) and max( ) are respectively the minimum and maximum of their

arguments.

With the formalities of the energy deﬁnitions taken care of, we can now explore

the working forms for the DOS for both metallic and semiconducting nanotubes.

For metallic zigzag nanotubes, the DOS at the Fermi energy (located at k = 0) is of

primary interest. The band index for the ﬁrst subband is j = 2n/3 with a fourfold

energy degeneracy at the Fermi energy (a factor of 2 due to subband degeneracy

and another factor of 2 due to point degeneracy of the conduction and valence

bands). Substituting j = 2n/3 and k = 0 into Eq. (5.10) gives the DOS at the

Fermi energy (in short, the metallic DOS) for all metallic zigzag nanotubes:

= g

) =

√

3aπγ

∼ 2 ×10

−1

= 2nm

−1

. (5.18)

Notably, g

is independent of chirality and can be viewed as a material constant.

Invariably, because it is independent of chirality, we might suspect that Eq. (5.18)

will apply to all metallic nanotubes of arbitrary chirality, and this is in fact the

case.

Semiconducting zigzag CNTs can employ a simpler form of Eq. (5.10) for

routine analysis. For the lowest subbands which are of greatest relevance, E

vh2

much larger than the applicable electron energies (Eq. (5.12) >γ  E). Hence,

in the limit E

vh2

 E

, Eq. (5.10) reduces to

(E, j) =

√

3aπ E

vh2

|E|



− E

vh1

vh2

|E|



− E

vh1

. (5.19)

R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes

(Imperial College Press, 1998) Chapter 4.