Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

5.8 Carrier density 119

Energy (eV)

Effective mass (m*/m

)

0 0.1 0.2 0.3

0.2

0.4

0.6

=1 nm

=1.5 nm

=2 nm

=2.5 nm

Fig. 5.6 Effective mass of the ﬁrst conduction subband for 1 nm (13, 0), 1.5 nm (19, 0), 2 nm

(26, 0), and 2.5 nm (32, 0) nanotubes. The energies have been normalized such that the

band minimum is at 0 eV.

has been used to model transport in CNT ﬁeld-effect transistors.

The band min-

imum m

∗

has a sublinear dependence on bandgap, and for a 1.5 nm (19, 0) CNT

has a value m

∗

∼ 0.046m

,(γ = 3.1 eV, E

∼ 0.58 eV, and m

is the rest mass).

A plot of the effective mass for selected semiconducting nanotubes is shown in

Figure 5.6.

5.8 Carrier density

The density of charge carriers (electrons or holes) is a central property of semi-

conductors and is often invaluable in determining charge and heat transport in

nanotube devices. We will focus on the electron carrier density with the implicit

understanding that the mathematical techniques and results apply equally well to

holes owing to the electron–hole symmetry in the CNT band structure. The zigzag

semiconducting nanotube is most amenable to analytical treatment and, as such,

its DOS will be in use in the subsequent analysis. However, the results for the

carrier density can be applied to arbitrary chiral nanotubes, as discussed at the end

of this section. The electron carrier density n

per subband is the total number of

occupied states in the subband:

(j) =



F(E)g

(E, j) dE. (5.56)

For the lowest subbands, C

and C

are equal to E

vh1

and E

respectively. F(E)

is the Fermi–Dirac distribution, given by

F(E) =

1 + e

(E−E

)/kT

, (5.57)

120 Chapter 5 Carbon nanotube equilibrium properties

where E

is the Fermi energy,

k is Boltzmann’s constant,

and T is the temper-

ature. Equation (5.56) does not have an exact analytical solution. However, under

certain approximations, an algebraic solution is accessible. To begin, we make the

approximation that the top of the band (C

) is much greater than the bottom of the

band (C

) and, owing to the rapidly decaying tail of the Fermi function, there is

negligible error taking the upper limit of the integral to inﬁnity. This approximation

is justiﬁed by inspection of Eq. (5.27). Using Eq. (5.19) for g

, the simpliﬁed the

carrier density integral is

(j) =

vh2



∞

vh1

1 + e

(E−E

)/kT



− E

vh1

dE,

(j) =

γ E

vh1

vh2



∞

1 + exp(zt − z

)

√

− 1

dt, (5.58)

where we have made some substitutions for simplicity (t = E/E

vh1

, z = E

vh1

/kT ,

and z

= E

/kT ).

Alas, this simpliﬁed integral does not have a closed-form analytical solution.

To proceed, we will develop formulas for the carrier density based on restricting

the position of the Fermi energy relative to the band bottom. Perhaps the most

elementary restriction of E

is the non-degenerate assumption which restricts

the Fermi energy to 3kT below the band bottom (E

≤ C

− 3kT ) and is

broadly used in bulk semiconductor physics.

Under this condition, the Fermi–

Dirac distribution can be approximated by the Maxwell–Boltzmann distribution

F(E) ≈ exp[(E

−E)/kT ].

Invariably, owing to the rapidly decaying exponen-

tial tail of the Maxwell–Boltzmann distribution, only the ﬁrst subband contributes

an appreciable number of carriers. A graphical illustration of the DOS, the Fermi–

Dirac distributions, and the implications of the non-degenerate approximation is

shown in Figure 5.7. The resulting non-degenerate carrier density n

e_nd

integral

for the ﬁrst subband is

e_nd

vh2





/kT

∞



−zt

√

− 1

dt, (5.59)

where the additional factor of 2 in the numerator is to account for the subband

degeneracy and E

vh1

has been substituted with E

/2. The integrand has the form

The Fermi energy is often used interchangeably with the phrase chemical potential µ in

semiconductor literature. Formally, E

is only deﬁned at T = 0 K and µ is the technical jargon at

ﬁnite temperatures. For convenience, we use E

for all temperatures.

The reader should be aware to distinguish the symbol k depending on the context, i.e. whether it is

used to symbolize wavevector or Boltzmann’s constant. It is often obvious when it is used for the

latter, as it will be multiplied with temperature.

R. F. Pierret, Semiconductor Device Fundamentals (Addison-Wesley, 1996), Chapter 2.

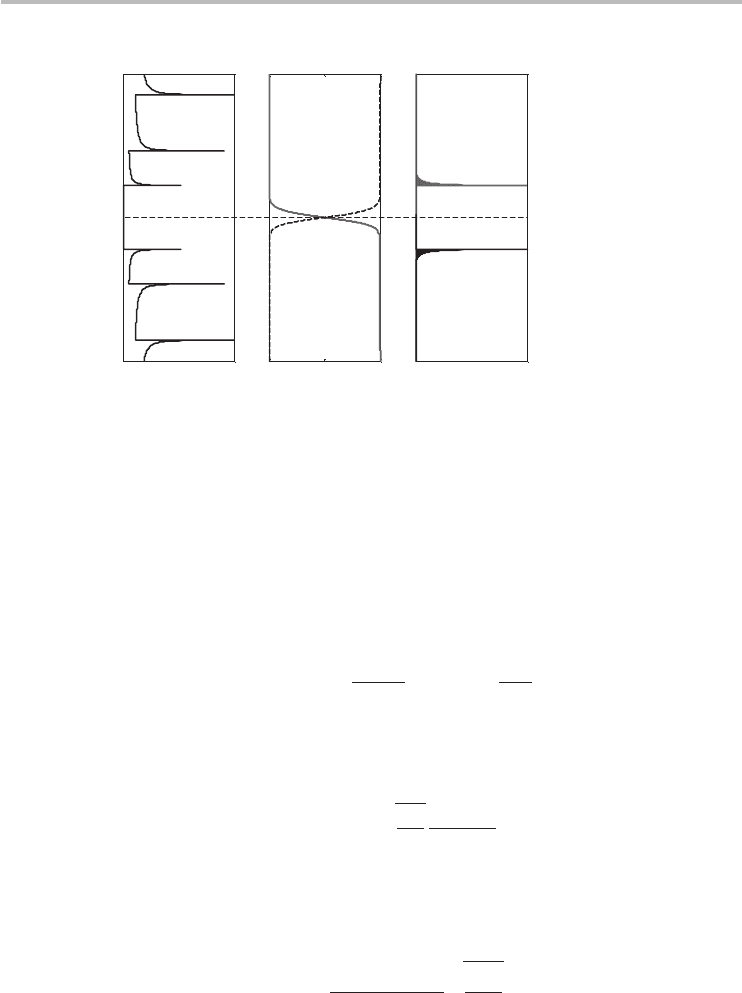
5.8 Carrier density 121

DOS (arb. units)

Energy

F (E)

0 0.5 1

DOS*F (E)

(arb. units)

(b)(a) (c)

Fig. 5.7 Illustrative plot of the DOS and Fermi–Dirac distribution at equilibrium. (a) Conduction

and valence band DOS. (b) F(E) for electrons (solid) and holes (dashed). (c) DOS

multiplied by the Fermi–Dirac function (has the form of a modiﬁed Bessel function of the

second kind), showing that, essentially, only the ﬁrst subband contributes appreciably to

carrier density at equilibrium.

of the modiﬁed Bessel function of the second kind, which looks similar to the

curve illustrated in Figure 5.7c. Fortunately, the integral has a solution given by

e_nd

γ E

vh2

/kT



2kT



, (5.60)

where K

(z) is the modiﬁed Bessel function of the second kind of order one. An

accurate closed-form approximation for K

(z) is given as

(z) ≈

(1 + 2z)

−z

. (5.61)

It follows that the non-degenerate carrier density can be expressed algebraically as

e_nd

= n

/kT

, (5.62)

γ(E

+ kT )

vh2



πkT

−E

/2kT

, (5.63)

The integral is interestingly the deﬁnition of the modiﬁed Bessel function of the second kind of

order one. See M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions with

Formulas, Graphs and Mathematical Tables, 10th edn (Washington, DC: US Government

Printing Ofﬁce, 1972).

D. Akinwande, Y. Nishi and H.-S. P. Wong, An analytical derivation of the density of states,

effective mass, and carrier density for achiral carbon nanotubes. IEEE Trans. Electron Devices, 55

(2008) 287–97.

122 Chapter 5 Carbon nanotube equilibrium properties

where n

is the temperature-dependent intrinsic (or equilibrium) carrier density

deﬁned for E

= 0. A more convenient form for hand analysis for n

is achievable

by substituting E

vh2

≈ E

vh1

+ 2γ :

γ(E

+ kT )

+ 4γ



πkT

−E

/2kT

. (5.64)

Likewise, the non-degenerate hole carrier density is

h_nd

= n

−E

/kT

. (5.65)

Figure 5.8a shows the non-degenerate electron carrier density for semiconducting

zigzag nanotubes where the exponential dependence seen in 3D semiconductors

is also observed in 1D CNTs. Moreover, the formulas for the non-degenerate

carrier density for CNTs (Eqs (5.62)–(5.65)) have essentially the same functional

form as for 3D bulk semiconductors.

Quite interestingly, the form of the carrier

density and its dependence on bandgap, temperature, and Fermi energy can be

deduced simply by dimensional scaling of the 3D bulk carrier density, speciﬁcally

by scaling the partition function in statistical mechanics from three dimensions to

one dimension, as shown in the appendix of the article referenced in footnote 16.

Aquestion of interest is how the intrinsic carrier density of CNTs compares with

the intrinsic carrier densities of bulk semiconductors. To make this comparison

possible, the CNT carrier density is normalized to the volume of the nanotube

and compared against bulk semiconductors in Figure 5.8b. It is clear from the

ﬁgure that nanotubes offer more carriers per unit volume, and this partly explains

2 3 4 5 6 7 8

d=1 nm

d=1.5 nm

d=2 nm

d=3 nm

Carrier density (n

) (cm

–1

)

- E

)/kT

(a) (b)

200 300 400 500

T (K)

Intrinsic carrier density (cm

–3

)

1.5 nmCNT (0.58 eV)

GaAs(1.42 eV)

Si(1.12 eV)

Ge(0.66 eV)

(0.84 eV)

1 nm

CNT

Fig. 5.8 (a) CNT carrier density using Eq. (5.60) as a function of the Fermi level at room

temperature. Within the non-degenerate range (C

− E

> 3kT ), the maximum |error|

< 3.5 %, and |error| < 6% if Eq. (5.62) is used. (b) The intrinsic carrier density of ∼1nm

(13, 0) and ∼1.5 nm (19, 0) nanotubes (normalized to the volume of the nanotube),

compared with the intrinsic carrier densities of bulk semiconductors.

The numbers in

parentheses are the respective bandgaps.

5.8 Carrier density 123

the higher (dimensionally) normalized current in nanotube devices compared with

conventional semiconductor devices.

The non-degenerate carrier density is a ﬁrst step towards our initial goal of

obtaining an analytical expression for the carrier density in CNTs. We now seek a

more general expression for the carrier density that accounts for positions of the

Fermi energy relative to the conduction band minima. To that end, Guo et al.

have shown that up to two subbands are signiﬁcant in determining charge transport

in practical nanotube transistors. This implies that, for the most part, only the ﬁrst

two subbands participate in contributing carriers to the overall carrier density. In

that light, Liang et al.

developed a semi-empirical analytical formula for the

carrier density in CNTs including the ﬁrst two subbands. For convenience, we will

refer to it as the two-subband carrier density, which is given as

≈



j=1

(j) =



j=1

/2kT

1 + A e

αx

+βx

, x

− E

2kT

, (5.66)

≈



j=1

(j) =



j=1

/2kT

1 + A e

αx

+βx

, x

−E

− 2E

2kT

, (5.67)

where α, β, and A are ﬁtting parameters and the sum is over the ﬁrst two subbands.

Within the two-subband approximation the relative positions of the Fermi energy

considered are max(E

≤ C

) for electrons and min(E

≥ V

for holes (see

Figure 5.2 for visual positions of C

and V

in the CNT band structure). For

semiconducting zigzag nanotubes of diameters from 1 to 4 nm at temperatures

within the practical range of 220 K to 375 K, the values of the ﬁtting parameters

with highest accuracy are α = 0.88, β = 2.41×10

–3

, and A = 0.63, resulting in an

error <6% compared with NNTB numerical computations. Fitting parameters for

a greater range of CNT diameters and temperatures are also discussed in the work

ofLiangetal.

Figure5.9isacomparisonbetweenthenumericalandanalytical

electron carrier density at room temperature for selected nanotubes showing strong

agreement. An attractive property of the semi-empirical carrier density formulas

is that they reduce to the non-degenerate carrier density formula when E

is within

the non-degenerate limit because the denominator of Eq. (5.66) approaches unity.

It is worthwhile keeping in mind that the non-degenerate and two-subband

carrier density expressions can be applied to determine the carrier densities of

arbitrary (n, m) semiconducting nanotubes because the energy range of interest

J. Guo, A. Javey, H. Dai and M. Lundstrom, Performance analysis and design optimization of near

ballistic carbon nanotube ﬁeld-effect transistors. IEEE IEDM Tech. Digest, (2004) 703–6.

J. Liang, D. Akinwande and H.-S. P. Wong, Carrier density and quantum capacitance for

semiconducting carbon nanotubes. J. Appl. Phys., 104 (2008) 064515.

The reader should be aware that j = 1 or 2 in this context refers to the ﬁrst or second subband, not

the value of the subband index itself. For example, the value of the subband index for the ﬁrst

subband is round (2n/3), where n is the zigzag chiral integer.

124 Chapter 5 Carbon nanotube equilibrium properties

0 5 10 15

Symbols:numerial

Lines: analytical

Atomic density of (19,0) carbon nanotube

d = 2 nm

d= 3 nm

d = 1 nm

Carrier density (n

) (cm

–1

)

-C

)/kT

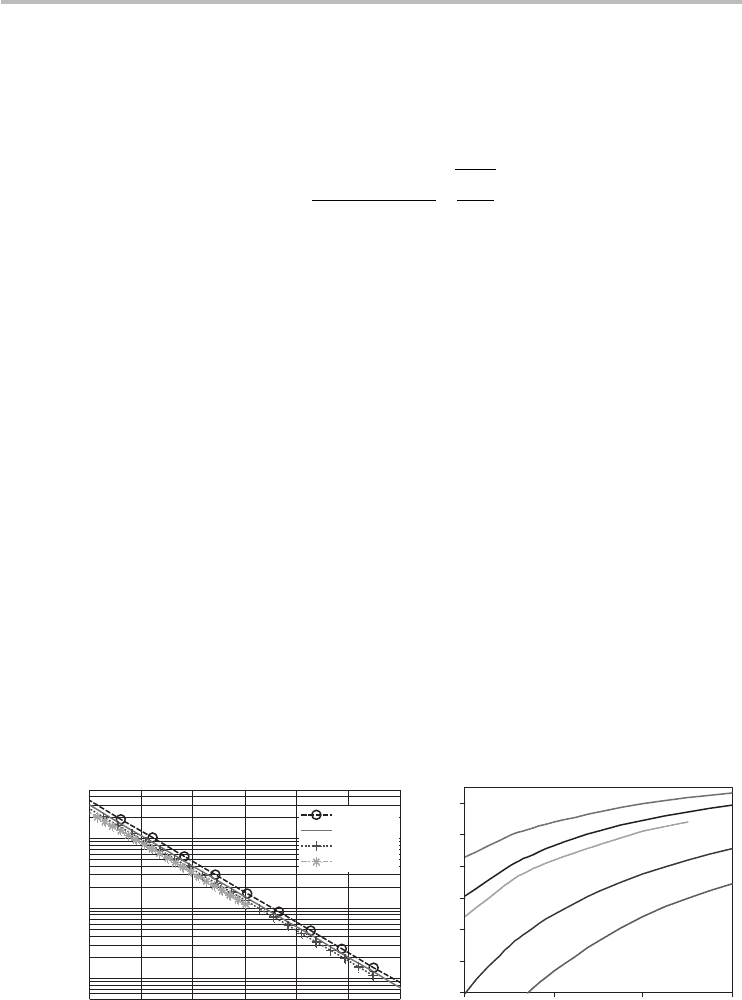
Fig. 5.9

Comparison of the two-subband analytical electron carrier density and numerical

computation of the carrier density at room temperature showing good agreement (error

< ± 5 %). The dashed line is the atomic density of (19, 0) zigzag CNT for reference.

considered in the carrier density derivation clearly falls below the bottom of the

third subband where the universal DOS idea applies.

5.9 Summary

We have explored the essential equilibrium properties of CNTs in this chapter.

Much of the effort was to obtain an understanding of the gradient and curvature of

the CNT band structure. For example, the band gradient is captured in the DOS,

and the band curvature informs us of the effective mass of charge carriers. We

found that the DOS which reﬂects the 1D nature of nanotubes is a very important

property that is directly related to many other electronic properties, such as electron

velocity and carrier density. It is not an exaggeration to assert that understanding

the CNT DOS is essential to gaining insight about electron behavior in nanotube

devices.

The key result of this chapter is the development of analytical equations to

describe the equilibrium properties. Particularly useful is that, by employing the

universal DOS idea, the equations or formulas developed can be applied to arbitrary

(n, m) nanotubes for practical device applications. Talking about practical appli-

cations, it is important to keep in mind that interesting devices generally do not

operate in equilibrium, because of external applied ﬁelds, which serves to provide

us a degree of freedom to control electron transport. Nonetheless, the departure

from equilibrium is often considered negligible or at least weak enough to be

5.10 Problem set 125

ignored to ﬁrst order. This is especially true for low-energy excitation of electrons

in nanotubes. In this limit, which is frequently referred to as quasi-equilibrium, the

Fermi–Dirac function remains an accurate distribution of occupied states. At high

energies,self-consistent numerical computation is typically employed to determine

the non-equilibrium properties, such as the carrier velocity and carrier density.

Owing to scaling of conventional semiconductor technology, it is expected that

the majority of device applications of CNTs will be at low operating energies.

5.10 Problem set

All the problems are intended to exercise and reﬁne analytical techniques while

providing important insights. If a particular problem is not clear, the reader is

encouraged to re-study the appropriate sections. Invariably, some problems will

involve making reasonable approximations or assumptions beyond what is already

stated in the speciﬁc question in order to obtain a ﬁnal answer. The reader should

not consider this frustrating, because this is obviously how problems are solved in

the real world.

5.1. Free-electron density of states in two and three dimensions.

Analysis and insights regarding the free-electron density of states in 1D space

become more relevant and useful when compared with the characteristic

density of states in 2D and 3D space. As a result, this exercise focuses on

deriving the DOS for free electrons in higher dimensions.

(a) Derive the 2D DOS of free electrons.

(b) Derive the 3D DOS of free electrons.

arbitrary units versus energy.

5.2. Higher subbands in metallic CNTs.

A linear dispersion is often assumed for armchair nanotubes (representative

of metallic CNTs) because at low energies only the ﬁrst subband contributes

to electron transport. To gauge the accuracy of this assumption, it is worth-

while determining the energy minimum of the second subband. This energy

minimum can be viewed as a threshold above which the linear dispersion no

longer holds.

(a) Determine analytically an expression for the second subband energy for

armchair CNTs.

(b) What is the diameter dependence of the second subband energy?

For an accessible discussion of non-equilibrium techniques for electron devices, see M. Lundstrom

and J. Guo, Nanoscale Transistors: Device Physics, Modeling and Simulation (Springer, 2006).

126 Chapter 5 Carbon nanotube equilibrium properties

the diameter dependence of the bandgap of semiconducting CNTs. Is the

functional dependence identical in both cases?

5.3. Density of states for armchair CNTs.

(a) Derive the DOS for armchair CNTs (representative of metallic CNTs)

considering only the ﬁrst subband.

(b) What is the effective mass for electrons in the ﬁrst subband of an armchair

nanotube?

(b) Derive an expression for the electron carrier density considering only the

contributions from the ﬁrst subband.

5.4. Higher subbands in semiconducting carbon nanotubes

For transistor applications, the ﬁrst two subbands of a semiconducting CNT

are often assumed to provide the lion’s share of electrical current, particularly

at low energies. In other words, the effects of higher subbands are typically

neglected. The validity of this assumption strictly depends on the position of

the Fermi level relative to the energy minima of higher subbands. For this

reason, it is useful to have equations for the energy minima of the higher

subbands, especially for small-bandgap CNTs.

(a) Determine analytically an expression for the third subband energy (in

terms of the diameter) for a semiconducting zigzag CNT.

(b) If any approximations are made to arrive at an analytical expression, quan-

tify the error compared with numerical evaluation of the third subband

energy.

5.5. Kataura plot for E

A plot of the transition energies between pairs of VHSs (E

) is commonly

called a Kataura plot, after Hiromichi Kataura, who investigated these tran-

sition energies. A plot of these transition energies is often used to aid in the

investigation and interpretation of the optical properties of CNTs, as well as

the identiﬁcation of CNTs.

(a) Plot the transition energies E

versus diameter for all nanotubes with

diameters ranging from 0.7 to 3 nm and i from1to3.

(b) What is the functional dependence of E

on the CNT diameter?

5.6. Effective mass comparison between zigzag CNTs and chiral CNTs.

We have frequently stated that the semiconducting zigzag nanotube is a good

convenient model for arbitrary semiconducting nanotubes in general. For

example, this has been shown to be true in terms of the DOS, which is related

5.10 Problem set 127

to the gradient of the energy dispersion. Let us explore this a bit further for the

effective mass parameter, which is related to the curvature of the dispersion.

(a) Numerically compute the effective mass for semiconducting chiral

nanotubes for diameters from 1 to 3 nm.

(b) Compare the numerically computed effective mass with the analytical

effective mass for semiconducting zigzag CNTs of the same diameter.

Quantify any discrepancy in percentage terms.

6 Ideal quantum electrical

properties

It seems that the fundamental idea pertaining to quanta is the impossibility

to consider an isolated quantity of energy without associating a particular

frequency to it.

Louis de Broglie (postulated electron waves)

6.1 Introduction

The goal of this chapter is to explore the excitation and motion of electron waves

under ideal conditions in a metallic conductor. By ideal conditions, we mean

that electrons can be excited and transported without any scattering or collision

involved. The excitation of electrons can be achieved by applying an external

potential to energize the electron waves to oscillate more frequently, which can

result in a netelectron motionin the presence of adriving electric ﬁeld, say between

two ends of a metallic conductor. It is advisable to commit to memory that the

absence of electron scattering is technically called ballistic transport; as such, the

metallic conductor in this case would be referred to as a ballistic conductor.

Electrically, the ideal excitation and motion of electrons in low dimensions,

such as in 1D space, is manifest in the form of a quantum conductance, quantum

capacitance, and kinetic inductance, which represents a different paradigm from

our classical electrostatic and magnetostatic ideas. The conductance and induc-

tance reﬂect the electrical properties of traveling electron waves which lead to

charge transport and energy storage, while the quantum capacitance accounts for

the intrinsic charge storage that comes about from exciting electrons with an elec-

tric potential. In macroscopic bulk metals, the quantum electrical properties are not

readily observable or accessible owing to the large number of mobile electrons at

hand and the frequent collisions involved.

Consequently, these quantum electrical

properties have only attracted signiﬁcant interest and scholarship over the last three

decades, in part due to manufacturing advancements and innovation in fabricating

We will elucidate on how the quantum electrical properties scale from nanoscopic to macroscopic

materials as we expand the discussion throughout the chapter.