Will D., Gebhardt N. (Hrsg.) Hydraulik: Grundlagen, Komponenten, Schaltungen
Подождите немного. Документ загружается.

98 4 Berechnungsgrundlagen
4.9.2 Modellierung und Simulation eines Antriebszustandes
Der 1. Schritt:
An Hand eines auf Abb. 4.29 basierenden Antriebszustandes wird beschrieben,
wie aus vielen kleinen Beziehungen und Bilanzen ein Gesamtmodell in Form ei-
nes Blockschaltbildes entsteht und wie dieses dann weiter behandelt werden kann.
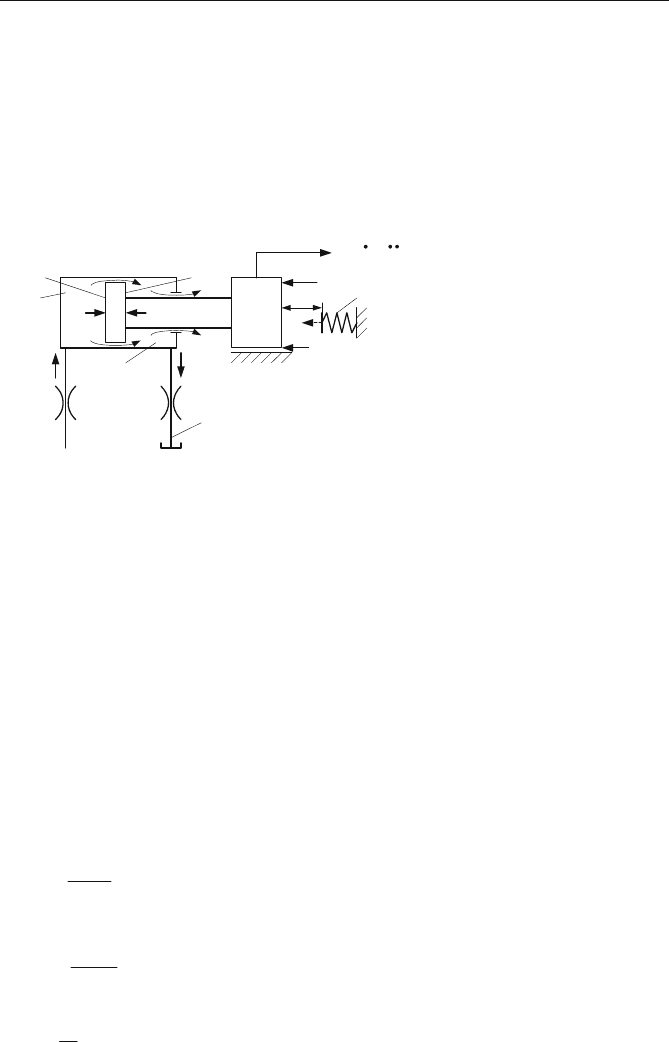
Abb. 4.50 zeigt das Schema des zu modellierenden Zustandes eines relativ ein-
fachen Antriebs.
Q
1
Q
2
F
L
m
p
1
p
2
A
1
A
2
Q
Li
Q
La
V
1
V
2
s, s, s
p = 0
F
A
F
1
F
2
c
F
Ri
p
0
G
Dr1
G
Dr2
a
Abb. 4.50 Schematische Darstellung des Bewegungszustandes eines Antriebs; der Arbeits-
zylinder besitze zwei Kapazitäten und zwei Leckspalte
Der Antrieb in Abb. 4.50 wird von einer Druckquelle mit dem Druck p
0
ver-
sorgt. Die Drosselstellen mit den Leitwerten G
Dr1
und G
Dr2
bestimmen wesentlich
die stationäre Geschwindigkeit des Arbeitskolbens vor dem Erreichen eines fe-
dernden Anschlages.
Der 2. Schritt:
Die Energiespeicher des Systems sind die bewegte Masse m, der federnde An-
schlag mit der Federkonstante c und die Kapazitäten C
1
= V
1
E
sowie C
2
= V
2
E
.
Die Leitungsvolumina wurden den an einem Arbeitspunkt als konstant an-
genommenen Arbeitszylindervolumina zugeschlagen. Die Zustandsgrößen sind p
1
,
p
2
, s
und s. Die Induktivität des Fluids wurde vernachlässigt.
Die Funktionen der Energiespeicher lauten (s. Tabellen 4.5 und 4.6 sowie die Gln.
(4.128 a) und (4.128 b)):
1
1
1
1
g
Q
V
p
E
,
³
dtpp
1
*
1
,
°
¯
°
®
t
,00
0
*
1
*
1
*
1
1
pfür
pfürp
p
,
(4.130 a)
2
2
2
1
g
Q
V
p
E
,
³
dtpp
2
*
2
,
°
¯
°
®
t
,00
0
*
2
*
2
*
2
2
pfür
pfürp
p
,
(4.130 b)
B
F
m
s
1
,
³
dtss
,
³
dtss
.
(4.130 c)

4.9 Modellierung und Berechnung des dynamischen Verhaltens 99
Der 3. Schritt:
Die folgenden Bilanzgleichungen der Volumenströme und der Kräfte können er-
mittelt werden (s. Tabellen 4.4 bis 4.6):
LiVg
QQQQ
111
.
(4.131 a)
LaLiVg
QQQQQ
222
(4.131 b)
LRCRPB
FFFFFF
21
(4.131 c)
Bei größeren Systemen empfiehlt es sich, die Funktionen der Speicher und die Bi-
lanzgleichungen schon jetzt in die Form des Blockschaltbildes zu bringen. Auf diesen
Schritt wird an dieser Stelle verzichtet.
Der 4. Schritt:
Der Arbeitszylinderausgänge sind über eine Drosselstelle mit nichtlinearen Funk-
tionen (s. Gl. (4.132 c)) mit einer Druckquelle bzw. mit dem Behälter verbunden.
Die weiteren statischen Grundbeziehungen des Systems lauten (s. Tabellen 4.4 bis
4.6):
sAQ
V
11
, sAQ
V
22
,.
(4.132 a)
)(
21
ppGQ
LiLi
,
2
pGQ
LaLa
,
(4.132 b)
)(
101011
ppsignppGQ
Dr
,
222
pGQ
Dr
,
(4.132 c)
111
pAF ,
222
pAF ,
(4.132 d)
skF
RP
, )(ssignFF
RCRC
,
¯
®
t
asfürcas
asfür
F
A
0
.
(4.132 e)
Der 5. Schritt:
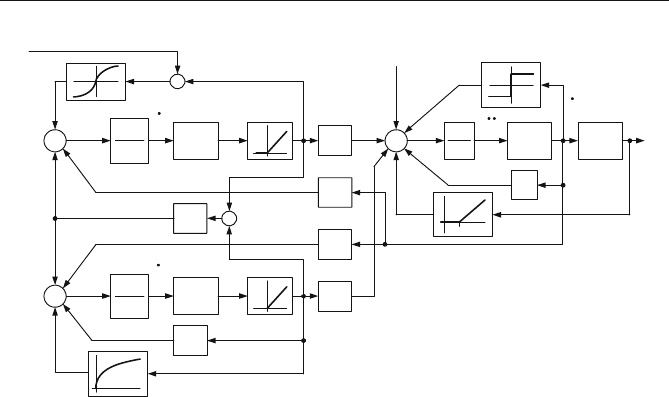
Sämtliche Beziehungen und Bilanzen aus den Gln. (4.130 a) bis (4.132 e) sind im
Blockschaltbild (Abb. 4.51) wieder zu finden. Die Zustandsgrößen sind die Aus-
gangsgrößen der Blöcke mit den Integrationsfunktionen. Die drei Bilanzgleichungen
sind in Abb. 4.51 an den größeren Summationsstellen zu erkennen. Die Ver-
knüpfungen der Teilsysteme entstehen vor allem über die Kolbenflächen A
1
und A
2
.
Verzweigungsstellen der Signalpfeile weisen darauf hin, dass eine physikalische
Größe auf mehr als ein Übertragungsglied einwirkt, der Druck p
2
z. B. auf eine
Fläche, zwei Leckleitwerte und einen Drosselspalt.
Die Kontrolle auf Vollständigkeit des Gesamtmodells mit Hilfe des Block-
schaltbildes ergibt:
Nur die echten Eingangsgrößen (p
0
und F
L
) besitzen „freie“ Pfeilenden.
Alle anderen Signale sind Ausgangsgrößen eines Blockes oder eines Summa-
tionsgliedes.
Alle Blöcke besitzen Ein- und Ausgangsgrößen.
100 4 Berechnungsgrundlagen
dt
³
1
V
1
ß
A
1
1
m
dt
³
dt
³
A
1
A
2
A
2
dt
³
1
V
2
ß
G
Li
G
La
k
-
-
-
-
-
Q
1
Q
2
Q
Li
Q
La
Q
g1
Q
g2
p
1
p
2
F
L
F
RP
ss
s
-
-
-
p
1
p
2
Q
V1
Q
V2
-
F
RC
F
B
F
1
F
2
-
F
A
a
-
p
0
p
1
*
p
2
*
Abb. 4.51 Das mathematische Modell des Bewegungszustandes des Antriebs in Abb. 4.50
als Blockschaltbild
Das Modell enthält die sechs Nichtlinearitäten
)(
101
ppfQ
,
)(
22
pfQ
,
)(
*
11
pfp , )(
*
22
pfp ,
)(sfF
RC
,
)(sfF
A
).
Die Modellstruktur ist relativ komplex, zu erkennen an der Vielzahl von Wir-
kungskreisen. Das Blockschaltbild bietet eine wichtige Möglichkeit der Kontrolle
über die richtige Festlegung der Vorzeichen: In allen Wirkungskreisen findet eine
ungerade Anzahl von Wirkungsumkehren statt, gekennzeichnet durch die Minus-
zeichen im Blockschaltbild („verallgemeinerte Lenzsche Regel“: Rückwirkungen
in technischen Systemen sind ihrer Ursache entgegengerichtet).
Der 6. Schritt:
Das dynamische Verhalten des Systems kann mit Hilfe der rechentechnischen Si-
mulation ermittelt werden. Ein Blockschaltbild wie in Abb. 4.51 kann relativ ein-
fach in ein blockorientiertes Simulationssystem überführt werden. Derartige Simu-
lationssysteme enthalten die benötigten linearen, einschließlich der Blöcke für die
Integration, und nichtlinearen Blöcke meist als Standard. (Diese Möglichkeit wird
auch in Kap. 8 und Kap. 14 mehrfach angewendet.)
Die rechentechnische Simulation kann nicht mit allgemeinen Werten der Para-
meter des Systems durchgeführt werden. Die Zeitverläufe der Eingangsgrößen
(hier p
0
und F
L
), die Anfangswerte der Zustandsgrößen sowie alle Werte von Mas-
sen, Volumina usw. müssen vor einer Simulation festgelegt werden.
4.9 Modellierung und Berechnung des dynamischen Verhaltens 101
Der Antrieb wird zum Zeitpunkt t = 0 mit Hilfe eines Wegeventils (in
Abb. 4.50 nicht dargestellt) an eine Druckquelle angeschlossen, deren Druck
p
0
= 100 bar = 10 N/mm
2
beträgt. An die Kolbenstange greife eine konstante äuße-
re Belastungskraft F
L
= 1000 N an.
Folgende Koeffizienten der Übertragungsglieder wurden gewählt:
Flächen: A
1
= 4,9 cm
2
= 490 mm
2
, A
2
= 3,4 cm
2
= 340 mm
2
,
Volumina: V
1
= 150 cm
3
= 15000 mm
3
, V
2
= 100 cm
3
= 10000 mm
3
,
Kompressibilität: E = 10
-3
mm
2
/N,
zu bewegende Lastmasse: m = 400 kg= 0,4 N s
2
/mm,
Federkonstante des Anschlages: c = 2000 N/mm,
Drosselleitwerte:
Ns
mm
bar
l
G
Ns
mm
bar
l
G
DrDr
4
2
4
1
31600
min/
6,0,52700
min/
0,1 ,
Leckleitwerte:
N
s
mm
ba
r
l
GG
LaLi
5
500
min/
003,0 ,
Faktor der geschwindigkeitsproportionalen Reibkraft: k = 5 N s/mm,
Coulombsche Reibkraft: F
RC
= 20 N,
Abstand a: a = 10 mm.
Als Anfangswerte der Zustandsgrößen wurden festgelegt:
p
1
*
(0) = 100 bar = 10 N/mm
2
(die Zeit bis zum Erreichen des angelegten Dru-
ckes p
0
ist in diesem System extrem klein und wurde vernachlässigt),
p
2
*
(0) = 0,
s(0) = 0 (diese Position des Arbeitskolbens liegt etwa in die Mitte seines
Hubbereiches),
0)0( s
.
Der 7. Schritt:
Das Blockschaltbild in Abb. 4.51 wird nunmehr in ein vom gewählten Simulati-
onssystem (z. B. Simulink oder BORIS) vorgegebenes Blockschaltbild überführt.
Für die Simulationen in diesem Buch kommt das System WinFACT/BORIS
[4.24] zum Einsatz.
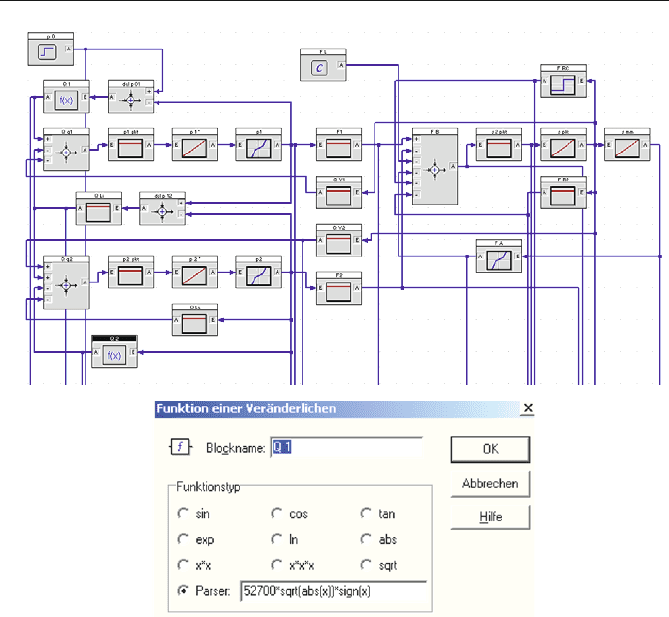
Das Simulations-Blockschaltbild in BORIS zeigt Abb. 4.52 a. Die Blöcke wur-
den annähernd so platziert wie im Blockschaltbild in Abb. 4.51. Die Blocknamen
wurden nach den Ausgangsgrößen festgelegt, da die aufgezeichneten Signale diese
Namen erhalten, wenn keine zusätzlichen Umbenennungen erfolgen.
Die Übertragungsfaktoren und die Funktionen wurden gemäß Abb. 4.51 in die
Blöcke eingetragen Die Blöcke werden per doppelten Mausklick geöffnet; die
Eingabemaske des nichtlinearen Blockes Q 1 mit der eingegebenen Funktion zeigt
Abb. 4.52 b.
102 4 Berechnungsgrundlagen
a
b
Abb. 4.52 Das Simulations-Blockschaltbild des Beispielsystems. a Struktur b Eingabe-
maske des nichtlinearen Blockes Q 1 mit der eingegebenen Funktion
Die nach unten abgeschnittenen Pfeile in Abb. 4.52 a zeigen zu den Zeitver-
laufsgliedern, mit deren Hilfe die interessierenden Signale aufgezeichnet werden,
und zu den Blöcken, in denen die Umrechnungen in die üblichen Dimensionen der
Hydraulik erfolgen.
Die Simulationsrechnungen erfolgen mit Signalen und Koeffizienten, die aus-
schließlich die Einheiten N, mm und s enthalten (s. o.), damit im Simulations-
modell selbst keine aufwendigen Umrechnungen erforderlich sind. Die Zeitver-
läufe der Drücke und Volumenströme in Abb. 4.53 werden in den üblichen
Dimensionen der Hydraulik dargestellt.
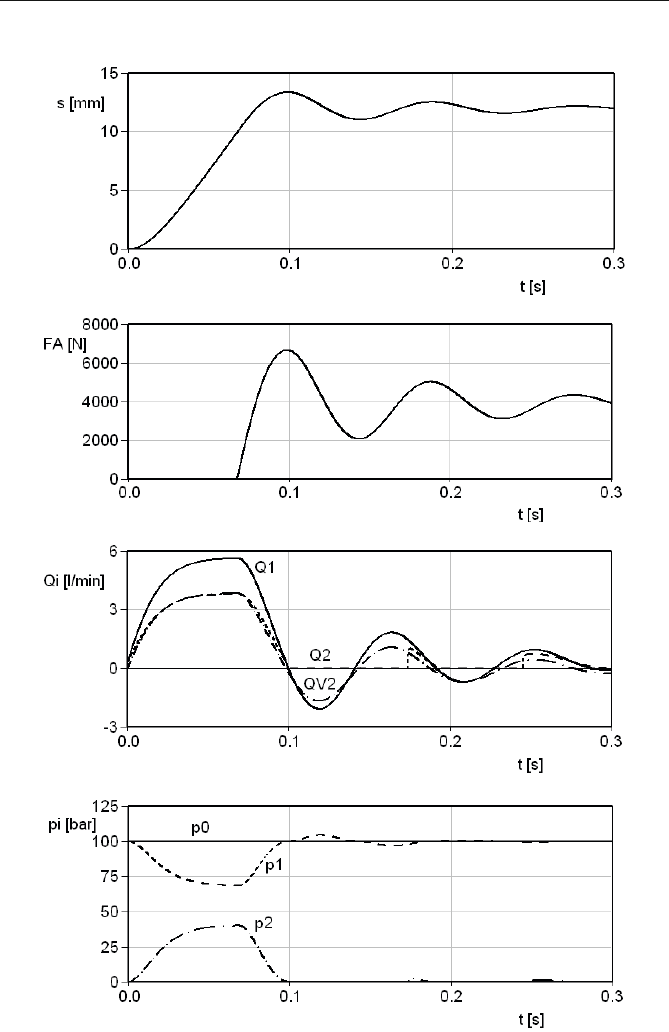
Aus dem Wegverlauf in Abb. 4.53 a ist die Grenze zwischen freier Bewegung
und der Verformung des nachgiebigen Anschlages zu erkennen: Der Weg
s = a = 10 mm wird nach etwa 67 ms erreicht. Danach wirkt die die Bewegung
bremsende Anschlagskraft F
A
(Abb. 4.53 b). Die Geschwindigkeit und die der Ge-
schwindigkeit proportionalen Verschiebevolumenströme, z. B. Q
V2
in Abb. 4.53 c,
streben schwingend nach null.
4.9 Modellierung und Berechnung des dynamischen Verhaltens 103
a
b
c
d
Abb. 4.53 Simulations-Ergebnisse des Modells in Abb. 4.51

104 4 Berechnungsgrundlagen
Der Volumenstrom Q
2
in Abb. 4.53 c hat einen von der Kavitation beein-
flussten Verlauf. Nach etwa 0,1 s werden die Geschwindigkeit und die Ver-
schiebevolumenströme Q
V1
und Q
V2
negativ. Das geometrische Volumen V
2
wird
größer, der Druck p
2
sinkt auf den Dampfdruck ab und die Druckdifferenz über
dem Drosselventil mit dem Leitwert G
Dr2
und damit auch der Volumenstrom Q
2
werden annähernd null. Das Differenzvolumen zwischen dem Ölvolumen und
dem geometrischen Volumen V
2
füllen Gas- und Dampfvolumina auf. Diese
werden bei negativem Q
V2
immer größer. Erst wenn bei positivem Q
V2
das
Ölvolumen und das geometrische Volumen V
2
wieder gleich groß werden, steigen
der Druck p
2
und der Volumenstrom Q
2
wieder an. Sie erreichen nur relativ kleine
Werte, diese allerdings fast sprungförmig, da die Kapazität C
2
sehr klein ist.
Der statische Endwert des Volumenstromes Q
2
wird im Wesentlichen vom in-
neren Leckleitwert G
Li
bestimmt (s. Gl. (4.132 b)).
Der Druck p
1
in der linken Zylinderseite erreicht keine Werte in der Nähe des
Dampfdruckes (Abb. 4.53 d), weshalb auf den Block p
1
= f ( p
1
*
) in Abb. 4.51 und
Abb. 4.52 a verzichtet werden könnte.
Anmerkung:
In Kap. 8 und Kap. 14 wird das dynamische Verhalten mehrerer Schaltungen
m. H. der Simulation nichtlinearer Modelle untersucht. Dabei wird auf viele der
Gln. (4.128 a) bis (4.132 e) und der in den Tabellen 4.4 bis 4.6 enthaltenen Funk-
tionen und Blöcke zurückgegriffen.
Der 8. Schritt:
Die Verifizierung des Modells mit Hilfe z. B. eines Experiments ist an dieser Stel-
le nicht möglich. Hilfreich sind oft Parametervariationen im Simulationsmodell,
um die Plausibilität des Modells zu ermitteln.
Eine auch in diesem Buch oft angewendete Methode ist die Modifikation der
Parameter des ursprünglichen Modells so, dass es ausreichend genau als lineares
Modell, als Differenzialgleichung oder Übertragungsfunktion, beschrieben werden
kann. Am aussagekräftigsten sind lineare Modelle 2. Ordnung, aus deren Eigen-
zeitkonstante T und Dämpfung D das dynamische Verhalten erkannt werden kann.
Im Folgenden wird dieser Weg, der in Kap. 8 und Kap. 14 vielfach beschritten
wird, auf der Basis des Beispieles in Abschn. 4.9.2 beschrieben.
4.9.3 Übertragungsfunktion eines linearen Antriebsmodells
Unter bestimmten Bedingungen kann der Antriebszustand in Abb. 4.50 linearisiert
werden:
Der Leitwert G
Dr2
wird auf null eingestellt, die Leckleitwerte G
Li
und G
La
sei-
en annähernd null.
Der Anschlag wird nicht erreicht. Die Speicherfähigkeit der Feder kommt
nicht zur Wirkung.
Die Coulombsche Reibung wird vernachlässigt.
Der Drücke p
1
und p
2
können nicht unter den Dampfdruck absinken.
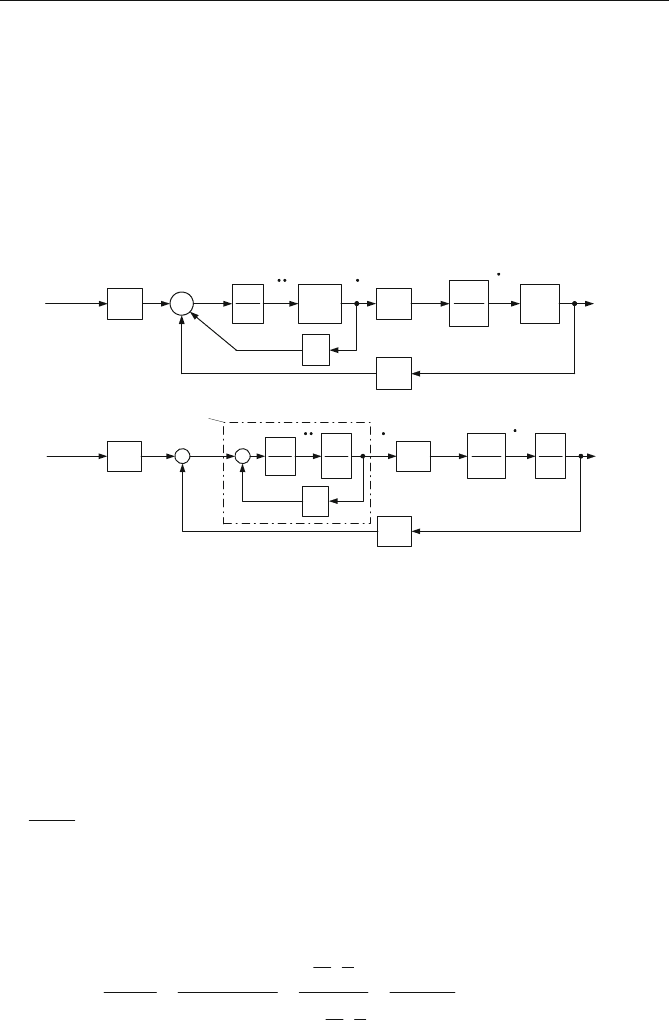
4.9 Modellierung und Berechnung des dynamischen Verhaltens 105
Wenn der Leitwert G
Dr1
eine Größenordnung größer gewählt wird als in
Abschn. 4.9.2 angegeben, kann die Energie-Speicherfähigkeit des Volumens
V
1
vernachlässigt werden, es ist
01
pp | .
Damit entfallen zwei der Energiespeicher und alle sechs Nichtlinearitäten. Es ent-
steht aus dem Blockschaltbild in Abb. 4.51 das lineare Modell 2. Ordnung in Abb.
4.54 a. Es interessiere der Verlauf des Druckes p
2
als Reaktion des sprung-
förmigen Anstieges des Druckes p
1
= p
0
. (Die Reaktion auf F
L
werde nicht ana-
lysiert, deshalb kann diese Kraft im Blockschaltbild entfallen.)
a
A
1
1
m
dt
³
k
p
1
= p
0
F
RP
ss
-
p
2
Q
V2
F
B
F
1
F
2
-
dt
³
1
V
2
ß
p
2
A
2
A
2
b
A
1
A
2
p
1
= p
0
s
Q
V2
F
1
F
2
-
p
2
A
2
1
V
2
ß
1
s
1
m
k
1
s
s
-
F
RP
p
2
'
F
G
H
(s)
Abb. 4.54 Blockschaltbild des linearisierten und vereinfachten Systems. a ausführliche
Darstellung
b Umwandlung der Integration m. H. des Laplaceoperators in die Funktion 1/s
Die Ermittlung einer Übertragungsfunktion setzt die Transformation des Mo-
dells in den Laplacebereich voraus. Alle Faktoren bleiben erhalten, aber die Blö-
cke mit der Integration über die Zeit führen auf Blöcke mit der Übertragungs-
funktion 1/s (s. Umwandlung der Abb. 4.54 a in Abb. 4.54 b). In einer Übertra-
gungsfunktion
G(s) wird das Verhältnis der gesuchten Ausgangsgröße x
a
zu einer
interessierenden Eingangsgröße x
e
als Funktion des Laplaceoperators s angegeben:
)(
)(
)(
sG
sx
s
x
e
a
.
G(s) Übertragungsfunktion
s Laplaceoperator
(4.133)
Über die zweimalige Anwendung der Kreisformel [4.23] kann aus Abb. 4.54 b die
gesuchte Übertragungsfunktion p
2
(s)/p
1
(s) ermittelt werden. Zuerst wird die Kreis-
formel auf die innere Schleife angewendet, sie wird zum Block G
H
(s):
smk
sm
k
sm
sG
sG
sF
ss
sG
Kreis
vorw
H
'
1
1
1
11
)(1
)(
)(
)(
)(
.
(4.134 a)
Der Ansatz für die gesuchte ÜTF lautet:
106 4 Berechnungsgrundlagen
sV
A
smk
sV
A
smk
A
sV
AsG
sV
AsGA
sG
sG
sp
sp
H
H
Kreis
vorw
E
E
E
E
2
2
2
2
21
2
2
2
2
21
1
2
11
1
11
1
)(1
1
)(
)(1
)(
)(
)(
.
(4.134 b)
Das führt in wenigen Schritten auf die Übertragungsfunktion in ihrer Normalform:
22
2
2
2
2
2
2
2
2
1
1
2
21
1
1
1
)(
)(
sTsDT
K
s
A
Vk
s
A
Vk
A
A
sp
s
p
EE
.
(4.134 c)
Aus dem Koeffizientenvergleich lassen sich der statische Übertragungsfaktor K,
die Eigenzeitkonstante T und die Dämpfung D ermitteln:
44,1
2
1
A
A
K
, mss
A
Vm
T
88,500588,0
2
2
E
,
037,0
22
2
2
2
m
V
A
k
D
DT
D
E
.
(4.134 d)
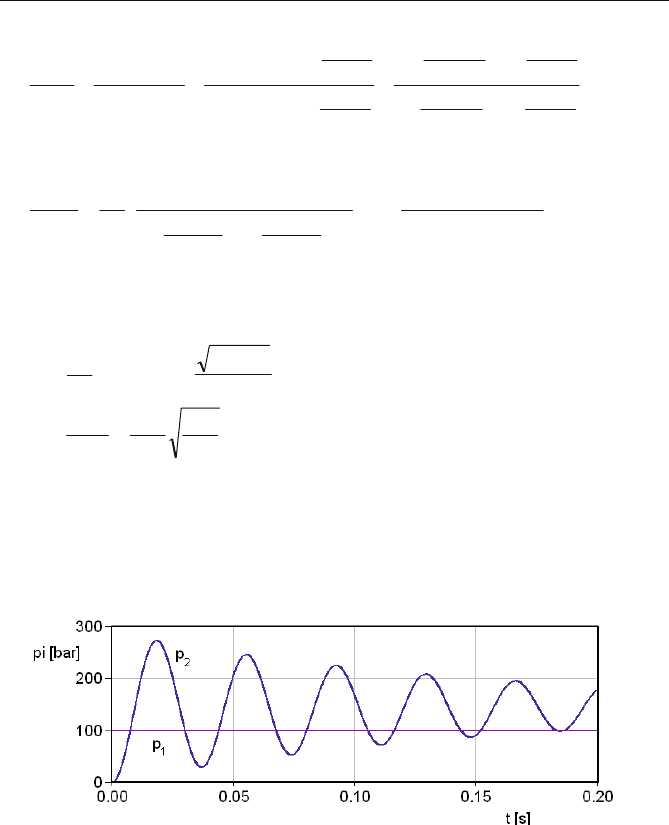
Die Sprungantwort des Modells mit der ÜTF in Gl. (4.134 c) unterscheidet sich
kaum von der des Modells in Abb. 4.51, wenn die in Abschn. 4.9.2 angegebenen
Parameterwerte mit den eingangs dieses Abschnittes vorgenommenen Modifi-
kationen eingestellt werden. Abb. 4.55 zeigt die Druckverläufe.
Abb. 4.55 Druckverläufe bei
0
LaLi
GG
und
0
2
Dr
G
Aus der Funktion der Dämpfung D in Gl. (4.134 d) ist zu erkennen, warum
hydraulische Antriebe oft schwach gedämpft sind: Die meist großen Massen ste-
hen im Nenner, die nur wenig kompressiblen Flüssigkeitsvolumina dagegen im
Zähler der Funktion. Die Dämpfung nimmt zu, wenn die Leckleitwerte größer
werden, dies wurde hier nicht detailliert analysiert.
In Kap. 14 werden für viele Schaltungen mit Hilfe der in Gl. (4.134 c) an-
gegebenen Normalform die Eigenzeitkonstante
T und Dämpfung D hergeleitet.
5 Grundstrukturen hydraulischer Kreisläufe
Die Gestaltung hydraulischer Kreisläufe wird beeinflusst von Aufgabenstellung
und Einsatzgebiet der Anlage, sowie durch die Größe der zu übertragenden Leis-
tung P. Die durch den Volumenstrom Q und den Druck p bestimmte hydraulische
Leistung wird dem Hydromotor zugeführt und dort in mechanische Leistung zu-
rücktransformiert (s. Kap. 2). Der Hydromotor kann ein Arbeitszylinder (trans-
latorische Bewegung) oder ein Rotationsmotor (drehende Bewegung) sein. Die für
konkrete Einsatzgebiete und Aufgabenstellungen zu wählenden Kreislauf-
strukturen werden in Kap. 14 behandelt.
Bei der Gestaltung hydraulischer Kreisläufe müssen die Grundstrukturen für
die Erzeugung der hydraulischen Leistung durch Volumenstrom- bzw. Druck-
quellen;
die Anordnung der Geräte und Komponenten im offenen oder geschlossenen
Kreislauf;
die Versorgung mehrerer Hydromotoren durch eine Volumenstromquelle bzw.
Druckquelle
beachtet werden.
5.1 Volumenstrom- und Druckquellen
5.1.1 Volumenstromquellen
Zur Wandlung der mechanischen Leistung des Antriebsmotors (Elektromotor
bzw. Verbrennungsmotor) in hydraulische Leistung dienen Pumpen, die nach dem
Verdrängerprinzip arbeiten. Das bedeutet, dass das während einer Umdrehung der
Antriebswelle aus dem Behälter in die Druckleitung der Hydraulikanlage ver-
drängte Flüssigkeitsvolumen konstant ist. Die Leckverluste der Pumpe und die
Verringerung des Flüssigkeitsvolumens durch Druckerhöhung (Kompression)
können in erster Näherung vernachlässigt werden (s. Abschn. 6.1).
Das pro Umdrehung der Antriebswelle verdrängte Volumen ist eine geo-
metrische Kenngröße der Pumpe und wird als Verdrängungsvolumen V be-
zeichnet. Die Baugröße einer Pumpe wird von ihrem Verdrängungsvolumen be-
stimmt. V kann konstant (Konstantpumpe) oder veränderbar (Stellpumpe) sein.
D. Will, N. Gebhardt (Hrsg.), Hydraulik,
DOI 10.1007/978-3-642-17243-4_5, © Springer-Verlag Berlin Heidelberg 2011
