Второв В.Б. Конспект лекций по ТАУ

Подождите немного. Документ загружается.

R e

I m

- + +

- 1

не охватывает

Пусть

 









pbk

Гурвицев полином (корни только левые).

Рассмотрим возможный вид АФХ при разных

АФХ разомкнутой системы не охватывает

 

0;1 j

или:

000 



следовательно, замкнутая система

устойчива.

Замкнутая система находится на границе устойчивого

колебательного типа.

АФХ разомкнутой системы охватывает

 

0;1 j

или:

0110 



следовательно, замкнутая система

неустойчива.

- 1

Пусть

0l

, а АФХ разомкнутой системы имеет вид:

R e

I m

- + +

- 1

Легко увидеть, что замкнутая система асимптотически устойчива, но теряет

устойчивость, как при увеличении, так и при уменьшении контурного коэффициента

Такая система называется условно-устойчивой.

Замечание: формулировка теоремы 22.1. сохраняет свою силу, если передаточная

функция разомкнутой системы кроме левых имеет также один нулевой полюс (смотри

дальше).

Второй случай:

0l

, но имеется один или несколько нулевых полюсов передаточной функции

разомкнутой системы.

Этот случай принципиально не отличается от первого, но имеет особенности

изображения частотных функций.

Пусть

 











pap

pbk

0p

полюс кратности



Пусть

1



, тогда

 

























9090

111





АФХ разомкнутой системы не охватывает точку

 

0;1 j

следовательно, замкнутая система

асимптотически устойчива. Полагаем, что нулевой

полюс принадлежит левой полуплоскости, тогда при

0



скачек аргумента

 

180



(поворот

вектора по часовой стрелке – дуга бесконечного

радиуса).

- 1

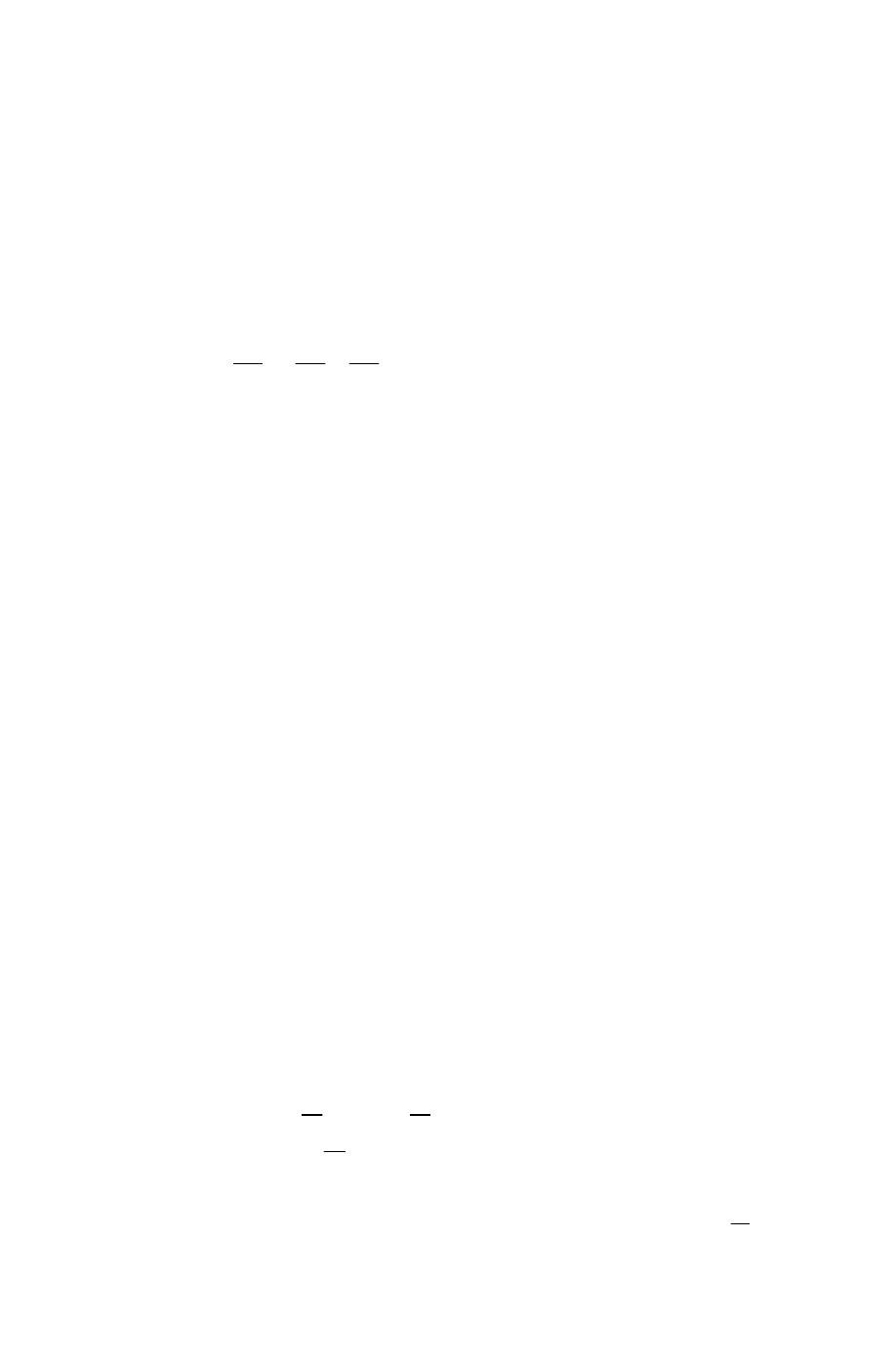
АФХ разомкнутой системы охватывает точку

 

0;1 j

или:

0110 



следовательно,

замкнутая система неустойчива. При изображении АФХ

только для



0

дополнение при

0



всегда

начинается на оси вещественных.

Пусть

2



, тогда

 

180

222

111











011 



следовательно, замкнутая система

асимптотически устойчива.

При

0



полное приращение угла равно

360

. В то время как при

1



дополнения не играют существенной роли (и его можно не делать, если остальные

полюсы левые), поскольку не влияет на охват точки

 

0;1 j

. При

2



дополнение

существенно и является обязательным. При дополнении АФХ, приращение аргумента

ЧПФ при

0



составляет



90

(если не рассматривать отрицательных частот).

Теорема 22.2. Если передаточная функция разомкнутой системы кроме левых полюсов

имеет один или несколько нулевых, то для асимптотической устойчивости замкнутой

системы необходимо и достаточно, чтобы АФХ разомкнутой системы дополненное при

0



дугой окружности бесконечного радиуса в направлении часовой стрелки не

охватывала точку

 

0;1 j

, т.е. чтобы

0



Третий случай:

имеется

правых полюсов, а остальные левые.

 















lln

jQl

Лемма

arg0





 













jDr

Лемма

arg0





, следовательно,

 













arg

, т.е.

вектор

 



должен поворачиваться вокруг начала координат (а вектор

 





вокруг точки

 

0;1 j

против часовой стрелки

раз для





раз для





Теорема 22.3. Если передаточная функция разомкнутой системы имеет

правых

полюсов, а остальные левые, то для асимптотической устойчивости замкнутой системы

необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала точку

 

0;1 j

- 1

направлении против часовой стрелки

раз при

















раз при





, или

что тоже самое















Замечание: если при

0



АФХ начинается на луче





1,

, то это соответствует

перехода через этот луч, т.е.





- 1

Теорема 22.4. Если передаточная функция разомкнутой системы имеет

правых

полюсов, а остальные левые или нулевые, то для асимптотической устойчивости

замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы

дополненное, в случае наличия нулевых полюсов при

0



, дугой бесконечного радиуса

в направлении часовой стрелки охватывала точку

 

0;1 j

. В случае наличия левых

полюсов при изменении





)0( 



, дугой бесконечного радиуса в

направлении против часовой стрелки













раз.

Замечание: В первом случае подпадает под эту формулировку

 

0l

Критерий Найквиста для ЛЧХ.

Теорема 22.5. Если передаточная функция разомкнутой системы имеет

правых, а

остальные левые полюсов, то для асимптотической устойчивости замкнутой системы

необходимо и достаточно, чтобы в диапазоне частот, где ЛАХ разомкнутой системы

лежит выше оси, разность между положительными (снизу вверх) и отрицательными

(сверху вниз) переходов ЛФХ через горизонтальную прямую

180

равнялась













Причём в случае наличия нулевых полюсов ЛФХ при

0



должна быть дополнена

надлежащим образом.

Замечание 1: дополнение при

0



должно быть выполнено так, чтобы скачёк ЛФХ

составил



90

Замечание 2: если

0l

, а

1



, то дополнение не обязательно. Если

0l

2



дополнение обязательно. Если

0l

дополнение обязательно независимо от



Замечание 3: если при

0



ЛФХ начинается на линии с ординатой

180

, то это

соответствует

перехода через эту линию.

Замечание 4: следующий случай непосредственно не подпадает под формулировку

теоремы 22.5, но может быть рассмотрен исходя из основной теоремы 22.4. если во всем

диапазоне частот ЛАХ разомкнутой системы лежит ниже оси абсцисс, то при

0l

замкнутая система заведомо устойчива, а при

0l

неустойчива, поскольку из

0L

следует

 

1



, т.е. АФХ разомкнутой системы не может охватить точку

 

0;1 j

Доказательство теоремы 22.5 следует из двух фактов:

Для точек перехода АФХ через луч





1;

 

1



, а аргумент

 

180



(смотри

точки а и б) им соответствуют точки а и б на

ЛЧХ, где

0L

, а

180



Переходу АФХ сверху вниз соответствует

переход ЛФХ через

180

снизу вверх

(точка б), и наоборот (точка а).

Следствие: (упрощенная формулировка для случая устойчивости разомкнутой

системы с монотонной ЛАХ). Если в передаточной функции разомкнутой системы есть

только левые полюсы и возможно еще один нулевой, а ЛАХ разомкнутой системы

монотонна, то для асимптотической устойчивости замкнутой системы необходимо и

достаточно, чтобы на частоте среза ЛФХ разомкнутой системы проходила выше уровня

180

§23. Качество САУ.

Качество САУ – степень соответствия системы к двум требованиям:

1. Регулируемая переменная

 

должна как можно лучше воспроизводить закон

изменения

 

2. Реакция

 

на внешнее воздействие

 

должна быть как можно слабее.

Оба требования можно объединить в требованиях ошибки

     

tytgte 

мгновенные значения

 

должны быть как можно меньше, а

 

должна как можно

быстрее затухать с течением времени. Поскольку реакция

 

или

 

имеет

переходную и вынужденную составляющую, то в понятии качества различают два

аспекта:

1. Качество динамики, т.е. характер переходных процессов.

2. Точность характеризуемая значениями установившейся ошибки при входных

воздействиях стандартного вида.

Для количественной характеристики качества динамики вводятся показатели качества

САУ. Они делятся на:

1. Прямые – показатели качества переходной характеристики.

- 1 8 0

R e

I m

- 1

2. Косвенные (оценки качества) – некоторым образом связаны с прямыми

показателями качества.

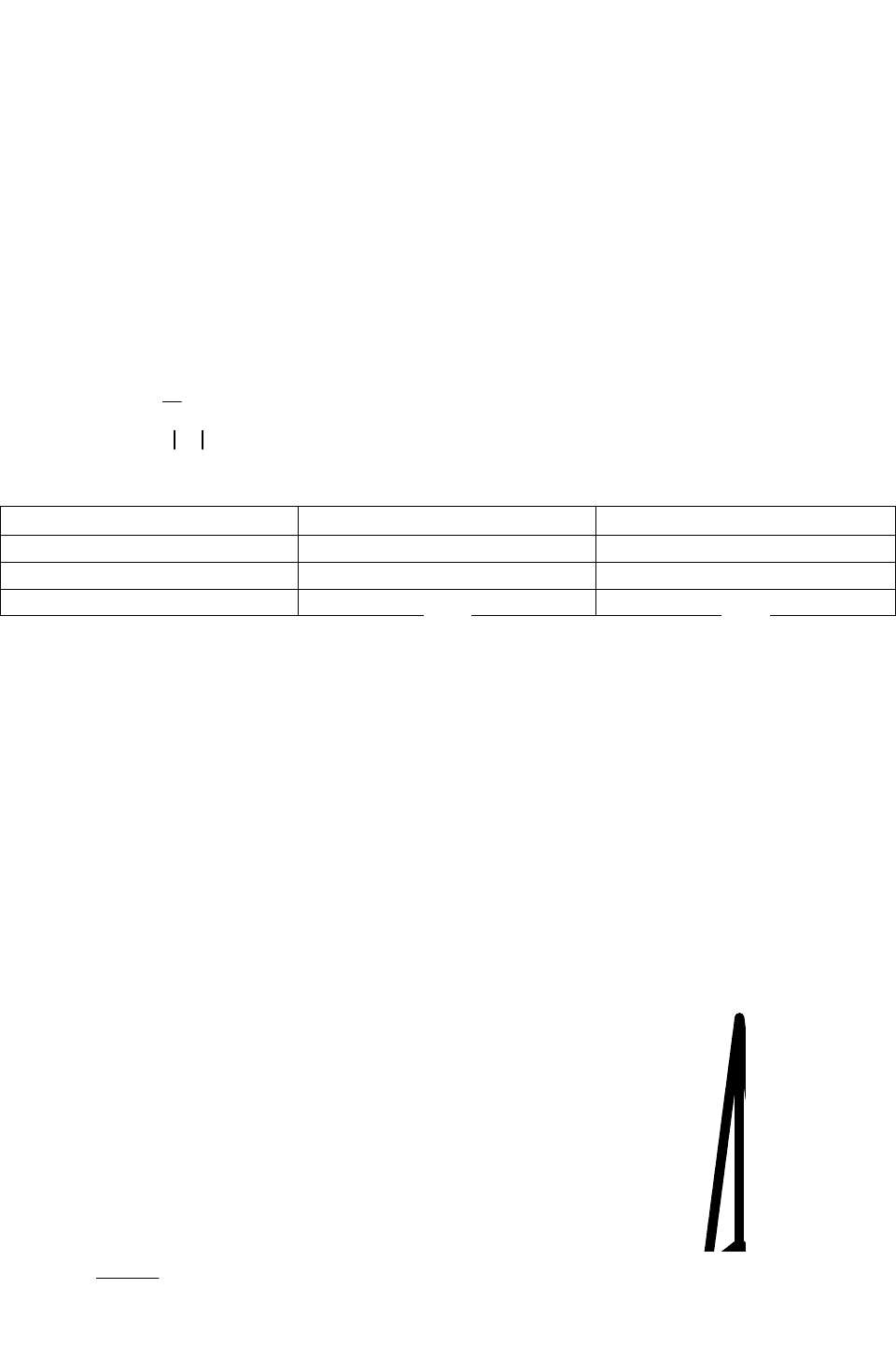
Показатели качества переходной характеристики.

m a x

h ( t )

ÊÎÌÏÀÑ-3D LT V7 (íåêîììåð÷åñêàÿ âåðñèÿ)

ÊÎÌÏÀÑ V7 (ñ) 2003-2004 ÇÀÎ ÀÑÊÎÍ, Ðîññèÿ. Âñå ïðàâà çàùèùåíû.

1. Время регулирования

 



 hhtht

для всех

tt 

, где

05.0

;

2. Время перерегулирования

%100

max











;

3. Время нарастания

 

 



 hthtt

:min

;

Частотные оценки качества.

1. Частота среза

 

0: 

cс



;







3 





(23.1)

Оценка вида (23.1) справедлива и для произвольной ЛАХ если:

1. Коэффициент наклона ЛАХ при





составляет

декдБ20

;

2. Протяженность этого участка не менее

дек5.1

;

Вообще

связано не только с



, но и со степенью демпфирования системы

 





11.0 



Запасы устойчивости.

 По модулю

 По фазе



- 1

I m

R e

L m

log20

Чем меньше

, тем больше запас по модулю. Если бы точка б совместилась с

точкой

 

0;1 j

, то система вышла бы на границу устойчивости. Чем меньше запасы

устойчивости, тем более склона система к колебаниям и тем больше перерегулирование.

Система

дБLm,



Плохая

8

30

Средняя

158

5030 

Хорошая

15

50

На значения запасов устойчивости наибольшее влияние оказывает коэффициент

наклона ЛАХ в окрестности



- 1

- 2

- 1

- 2

Для первой системы



больше чем для второй.

Показатель колебательности.

A ( 0 )

A m a x

A (

) - À × Õ ç à ì ê í ó ò î é ñ è ñ ò å ì û

 

max

M 

Чем больше М, тем больше



Хорошая система имеет

2.1M

;

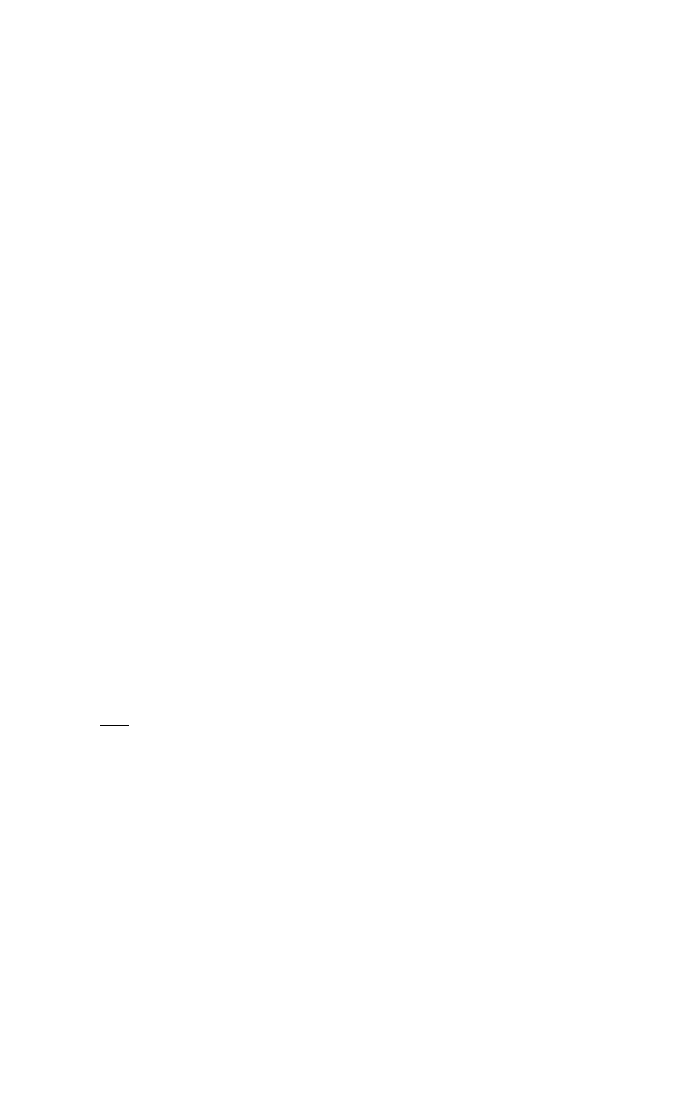
Средняя система

5.12.1  M

;

Полоса пропускания

A ( 0 )

0 . 7 0 7 A ( 0 )

Является мерой быстродействия системы.

3 ä Á



3 

В целом для САУ

связано с



примерно, так же как и с



Корневые оценки качества.

1. Степень устойчивости



. Расстояние от мнимой оси до ближайшего к ней корня

характеристического полинома замкнутой системы или пары сопряженных корней.

Является мерой быстродействия системы, поскольку та составляющая свободного

решения, которая определяется ближайшим к мнимой оси корнем (парой корней)

затухает наиболее медленней и следовательно определяет время переходного

процесса.

Рассмотрим систему третьего порядка:

Пусть

 

0,,;,

3,21





jpp

g h



 t



доминирует

 





tCtCe





sincos

доминирует





(23.2)





(23.3)

2. Колебательность



. Отношение модулей мнимой части и вещественной частей к

мнимой оси пары комплексно сопряженных корней









. Практически требуют,

чтобы все комплексные корни лежали в секторе с заданным углом



7.25.1 



3. Диаграмма Вышнеградского. Для системы третьего порядка позволяет оценить

качественную картину расположения корней характеристического полинома и

значения





Пусть

 

 apapapapD

, делим все на

 p

(23.4)

Вводим новую комплексную переменную



 p

подставляем в (23.4)

 BqAqq

(23.5)

где

;

A 

По критерию Гурвица асимптотическая устойчивость эквивалентна

1AB

Уравнения границы устойчивости:

BAB

;1 

Точка

3: BAC

0133

 qqq

 

q

3,2,1

q

:DC

:CE

:CF