Волков А.А. Курс физики
Подождите немного. Документ загружается.


a = x
1
=
x
0
1
+ V t
0
1
q
1 −
V
2
c
2
.
b = x
2
=
x
0
2
+ V t
0
2
q
1 −
V
2
c
2
.
t
0
1
= t
0
2
.
l
0
= x
2
= x
1
=
x
0
2
+ V t
0
2
− x
0
1
− V t
0
1
q
1 −
V
2
c
2
=
x
0
2
− x
0
1
q
1 −
V
2
c
2
=
l
0
q
1 −
V
2
c
2
⇒ l
0
= l
0
r
1 −
V
2
c
2
.
l
0
> l
0
.
Неподвижный отрезок длиннее движущегося.
Лоренцево сокращение — движущийся объект становится короче.
III.1.7 Интервал
Несмотря на то что x и t в отдельности изменяются от преобразований Лоренца, можно
подобрать величину, остающуюся при этом инвариантной (неизменной). Легко проверить,
что таким свойством обладает разность c
2
t
2
− x
2
. Действительно [1, стр. 150],
c
2
t
2
=
c
2
t
0
2
+
V
2
x
0
2
c
2
+ 2V x
0
t
0
1 −
V
2
c
2
,
x
2
=
x
0
2
+ V
2
t
0
2
+ 2V x
0
t
0
1 −
V
2
c
2
,
или
c
2
t
2
− x
2
= c
2
t
0
2
− x
0
2
≡ s
2
.
Величина s называется интервалом между двумя событиями: тем, которое произошло
в начальный момент t = 0 в начале координат, и другим, имевшим место в момент t в точке
x [1, стр. 151].
Слово
событие
можно понимать в самом обычном, житейском смысле, лишь бы
можно было определить его координаты и его время. Если первое событие отнесено не к
началу отсчета координат и времени, то интервал следует определить по разности отсчетов
[1, стр. 151]:
∆s
p
c
2
(t
2
− t
1
)
2
− (~r
2
−~r
1
)
2
=
p
c
2
(t
2
− t
1
)
2
− (x
2
− x
0
1
)
2
− (y
2
− y
0
1
)
2
− (z
2
− z
0
1
)
2
.
(∆s)
2
= c
2
(t
2
− t
1
)
2
− (~r
2
−~r
1
)
2
= c
2
(t
2
− t
1
)
2
− (x
2
− x
0
1
)
2
− (y
2
− y
0
1
)
2
− (z
2
− z
0
1
)
2
.
Бесконечно малый интервал между событиями d(∆s) определяется так [1, стр. 151]:
d(∆s)
2
= c
2
dt
2
− dx
2
− dy
2
− dz
2
= c
2
dt
0
2
−dx
0
2
− dy
0
2
− dz
0
2
| {z }
−dl
0
2
= c
2
dt
0
2
− dl
0
2
.
Записанный в таком виде интервал не связан с каким-либо направлением относитель-
ной скорости систем отсчета [1, стр. 151].
Браницкий А.А. 61 M∀TM∃X 2012

III.1.8 Квазиодновременные и последовательные события
Предположим, что у нас два мгновенных события.
В момент времени t
1
в точке ~r
1
произошла вспышка. Начинается распространение по-
рожденной электромагнитной волны со скоростью c. Успеет ли эта волна дойти до точки
~r
2
до того, как там в момент времени t
2
произойдет событие?
1.
|~r
2
−~r
1
|
c
< t
2
− t
1
.
Волна успела дойти. События последовательные. Первое событие произошло абсо-
лютно раньше второго.
2.
|~r
2
−~r
1
|
c
< t
1
− t
2
.
Волна не успела дойти. События последовательные. Второе событие произошло аб-
солютно раньше первого.
Для пары последовательных событий:
c
2
(t
2
− t
1
)
2
> (~r
2
−~r
1
)
2
.
(∆s)
2
> 0.
Квадрат интервала для последовательных событий положителен.
∆s =
p
(∆s)
2
∈ R.
Т. к. ∆s — инвариант, то ∆s — вещественный для всех последовательных событий.
Временной интервал: T
∆s
c
=
q
(t
2
− t
1
)
2
−
1
c
2
(~r
2
−~r
1
)
2
.
Временной интервал также является инвариантом.
|~r
2
−~r
1
|
c
> t
2
− t
1
|~r
2
−~r
1
|
c
> t
1
− t
2
такие события называются квазиодновременными.
Для пары квазиодновременных событий:
c
2
(t
2
− t
1
)
2
< (~r
2
−~r
1
)
2
.
(∆s)
2
< 0 ⇒ ∆s — мнимое.
Квадрат интервала для квазиодновременных событий отрицателен.
∆s =
p
(∆s)
2
∈ C \ R.
Т. к. ∆s — инвариант, то ∆s — мнимый для всех последовательных событий.
R =
p
−(∆s)
2
=
p
(~r
2
−~r
1
)
2
− c
2
(t
2
− t
1
)
2
.
R — простанственный интервал (инвариант).
Если есть 2 квазиодновременных события, то можно построить такую инерциальную
систему, в которой эти события будут одновременными.
Браницкий А.А. 62 M∀TM∃X 2012

Как строить?
V −?
A Ox — прямая, соединяющая ~r
1
и ~r
2
.
A Oy, Oz — произвольны.
t
0
2
= t
0
1
⇒ t
0
2
− t
0
1
= 0.
0 = t
0
2
− t
0
1
=
t
2
−
V x
2
c
2
q
1 −
V
2
c
2
−
t
1
−
V x
1
c
2
q
1 −
V
2
c
2
⇒ t
2
− t
1
=
V
c
2
(x
2
− x
1
).
V =
t
2
− t
1
x
2
− x
1
· c
2
.
Поскольку события квазиодновременные, то:
(x
2
− x
1
)
2
c
2
> (t
2
− t
1
)
2
.
1
c
2
>
(t
2
− t
1
)
2
(x
2
− x
1
)
2
| {z }
V
2
c
4
.
V
2
<
c
4
c
2
= c
2
⇒ V < c.
Т. с. построенная система координат будет реализуема на практике.
Для последовательных событий можно построить такую инерциальную систему отсче-
та, в которой эти события произойдут в одной точке пространства, но в разные моменты
времени.
Как строить?
V −?
A Ox — прямая, соединяющая ~r
1
и ~r
2
.
A Oy, Oz — произвольны.
x
0
2
= x
0
1
⇒ x
0
2
− x
0
1
= 0.
0 = x
0
2
− x
0
1
=
x
2
− V t
2
q
1 −
V
2
c
2
−
x
1
− V t
1
q
1 −
V
2
c
2
⇒ x
2
− x
1
= V (t
2
− t
1
) ⇒ V =
x
2
− x
1
t
2
− t
1
.
V =
t
2
− t
1
x
2
− x
1
· c
2
.
Поскольку события последовательные, то:
(x
2
− x
1
)
2
c
2
< (t
2
− t
1
)
2
.
1
c
2
<
(t
2
− t
1
)
2
(x
2
− x
1
)
2
| {z }
V
2
c
4
.
V
2
<
c
4
c
2
= c
2
⇒ V < c.
Т. с. построенная система координат будет реализуема на практике.
Только последовательные события могут быть связаны причинно-следственными свя-
зями. Для квазиодновременных событий нельзя вводить причинно-следственные связи.
Браницкий А.А. 63 M∀TM∃X 2012

III.2 Релятивистская механика
III.2.1 Функция Лагранжа
Второй закон Ньютона:
m ~w =
~
F .
Второй закон Ньютона был инвариантным преобразованием Галилея (т. е. работает
только тогда, когда
V
c
1).
Функция Лагранжа: L T − U, где T — кинетическая энергия, U — потенциальная
энергия.
Уравнение Лагранжа:
d
dt
∂L
∂ ˙q
j
−
∂L
∂q
j
= 0,
где q
1
, . . . , q
n
— обобщенные переменные координаты.
Траектория частицы:
S =
t
2
Z
t
1
Ldt — функционал действия.
S имеет экстремум при траектории, занимающей наименьшее время.
Для нахождения траектории нужно найти эктремум.
δS = 0 — принцип Гамильтона.
Релятивистская механика — механика, которая инвариантна относительно преобразо-
ваний Лоренца.
Будем рассматривать движение свободной материальной точки.
Будем искать действие свободной частицы в виде [1, стр. 158]:
S =
Z
αds, α = const.
В системе координат, связанной с точкой, точка неподвижна ⇒ ds = cdt
0
⇒
S =
Z
αcdt
0
.
v — скорость движения точки.
Перейдем теперь от действия к функции Лагранжа. Для этой цели представим беско-
нечно малый интервал так [1, стр. 158]:
ds = cdt
0
=
√
c
2
dt
2
− dl
2
= cdt
s
1 −
dl
dt
2
·
1
c
2
= c
r
1 −
v
2
c
2
dt.
Функция Лагранжа, инвариантная относительно преобразований Лоренца:
L
L
= αc
r
1 −
v
2
c
2
— функция Лагранжа для свободной точки.
Для классического случая:
L
L
= αc
r
1 −
v
2
c
2
v
c
1
≈ αc
1 −
1
2
v
2
c
2
= αc
|{z}
const
−
αv
2
2c
.
Браницкий А.А. 64 M∀TM∃X 2012
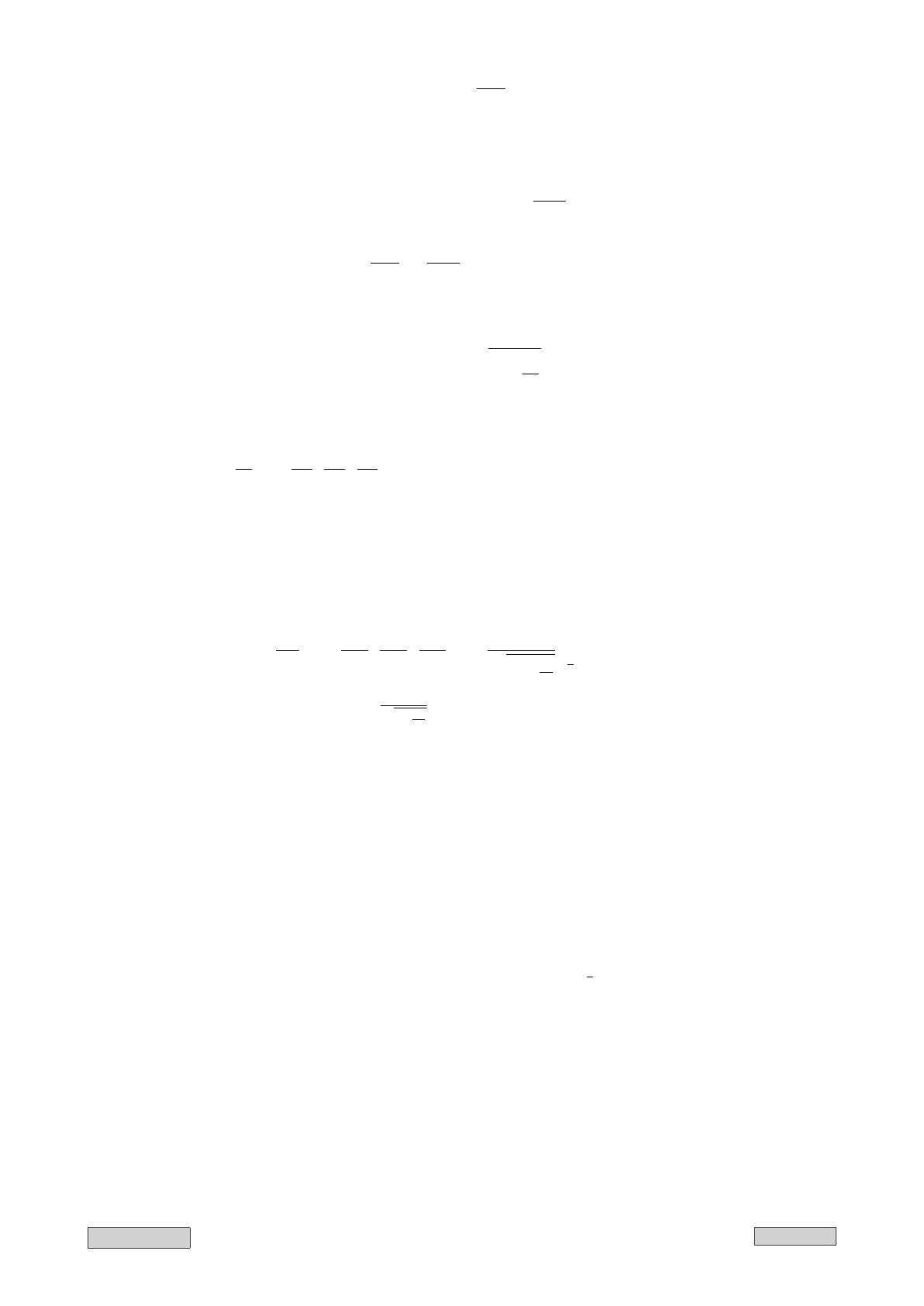
L
N
= −
αv
2
2c
.
Потенциальная энергия U = 0, если нет внешних сил.
В нашем случае U = 0, т. к. свободно движущаяся точка не имеет потенциальной
энергии.
L
N
= T − U
|{z}
0
= T =
mv
2
2
.
−
αv
2
2c
=
mv
2
2
⇒ α = −mc.
По смыслу здесь масса частицы m определена в ее собственной системе отсчета. Окон-
чательно имеем функцию Лагранжа в таком виде [1, стр. 158]:
L
L
= −mc
2
r
1 −
v
2
c
2
.
III.2.2 Импульс
Импульс: ~p =
∂L
∂~v
=
∂L
∂v
x
,
∂L
∂v
y
,
∂L
∂v
z
.
v — скорость движения материальной точки.
До этого мы рассматривали движение абстрактных объектов (систем координат).
Если на тело не действует сила, то оно либо покоится, либо движется равномерно
прямолинейно (первый закон Ньютона).
v — постоянна.
v
2
= v
2
x
+ v
2
y
+ v
2
z
.
~p =
∂L
∂~v
=
∂L
∂v
x
,
∂L
∂v
y
,
∂L
∂v
z
=
m~v
q
1 −
v
2
c
2
−−−→
v
c
1
~p
N
= m~v.
В некоторых книгах величину
m
q
1−
v
2
c
2
, т. е. коэффициент пропорциональности между
скоростью и импульсом, называют
массой движения
[1, стр. 159].
Движение материальных объектов невозможно при скоростях, равных c, т. к. импульс
неограниченно растет (бесконечно большой импульс надо прикладывать, а такое невоз-
можно). Это ограничение релятивистской теории.
p −−→
v→c
∞.
Можно раскрыть неопределенность, если положить m = 0.
По мере того как скорость частицы стремится к скорости света, импульс частицы рас-
тет до бесконечности [1, стр. 159].
Исключение может составлять только такая частица, масса которой равна нулю. Им-
пульс такой частицы дает при v = c неопределенность вида
0
0
и может остаться конечным.
Но тогда скорость подобной частицы всегда обязана быть равной c, потому что в против-
ном случае ее импульс тождественно обратится в нуль, и она никак не сможет вступить
во взаимодействие с какой-либо механической системой, т. е. не проявит физической ре-
альности [1, стр. 159].
Скорость, б´ольшая c, физически бессмысленна, потому что ей отвечали бы мнимые
значения импульса. Сверхсветовые частицы двигались бы с большей скоростью, чем пе-
редается между ними взаимодействие. Нетрудно представить себе абсурдные ситуации,
которые получались бы с частицами, движущимися быстрее, чем распространяется вза-
имодействие между ними. Не смог бы соблюдаться и принцип причинности. Исключение
Браницкий А.А. 65 M∀TM∃X 2012
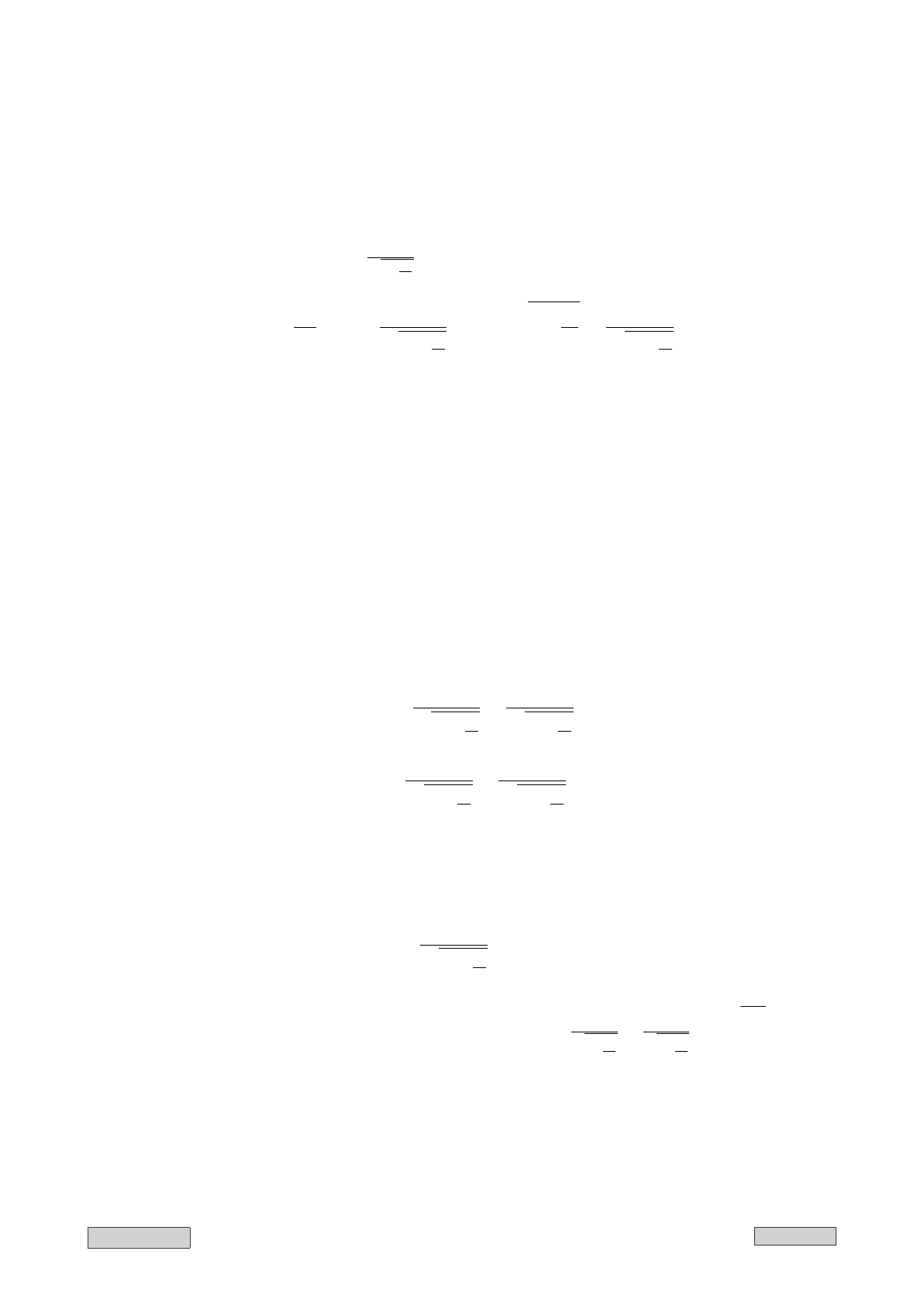
сверхсветовых скоростей связано с тем, что причинность никак не нарушается принципом
относительности. Причинность связывает между собой объективно происходящие собы-
тия, а понятие такого рода, как последовательность причин и следствий, не зависит от
выбора систем отсчета [1, стр. 159].
III.2.3 Энергия
m
0
— масса покоя (масса в классической теории).
Релятивистская масса: m
m
0
q
1−
v
2
c
2
.
Энергия:
E = ~v
∂L
∂~v
− L =
m
0
v
2
q
1 −
v
2
c
2
+ m
0
c
2
r
1 −
v
2
c
2
=
m
0
c
2
q
1 −
v
2
c
2
.
E = mc
2
—
энергия покоя массы
(энергия покоящейся массы)
(энергия Эйнштейна).
В классической теории энергию покоящейся массы мы считаем равной нулю (изменение
энергии дает работу).
Применим формулу энергии к сложной частице, способной к самопроизвольному распа-
ду на две новые частицы, например к ядру, распадающемуся на дочернее ядро и α-частицу.
Так как распад самопроизвольный, он обязан не внешнему воздействию на материнское
ядро, а каким-то особенностям его внутреннего движения. Следовательно, радиоактивный
распад — это процесс, происходящий в замкнутой системе, и полная энергия в этом случае
сохраняется. Энергия материнского ядра до распада равна сумме энергий дочернего ядра
и α-частицы после распада, когда взаимодействия между ними уже нет [1, стр. 160].
Считая теперь, что распадавшаяся частица покоилась, запишем выражение закона со-
хранения энергии для распада [1, стр. 160]:
m
P
c
2
=
m
1
c
2
q
1 −
v
2
1
c
2
+
m
2
c
2
q
1 −
v
2
2
c
2
.
m
P
=
m
1
q
1 −
v
2
1
c
2
+
m
2
q
1 −
v
2
2
c
2
.
m
P
> m
1
+ m
2
.
Изначально объект весил больше, чем после распада. Эта масса ушла на энергию раз-
рыва частиц.
Если определить разность
T ≡
mc
2
q
1 −
v
2
2
c
2
− mc
2
как кинетическую энергию частицы (при малых энергиях она переходит в
mv
2
2
), а mc
2
назвать энергией покоя, то из закона сохранения m
P
c
2
=
m
1
c
2
r
1−
v
2
1
c
2
+
m
2
c
2
r
1−
v
2
2
c
2
видно, что часть
энергии покоя сложной частицы превращается в кинетическую энергию частиц-продуктов
распада, а часть — в их энергию покоя. Закону сохранения удовлетворяют только полные
энергии E, а не кинетические T , потому что кинетическая энергия материнской части-
цы как целого до распада равна нулю и не может быть равной всегда положительной
кинетической энергии продуктов распада [1, стр. 160].
Браницкий А.А. 66 M∀TM∃X 2012

III.2.4 Преобразования Лоренца для импульса и энергии
p
x
=
mv
x
q
1 −
v
2
c
2
.
v
x
=
dx
dt
.
v — скорость частицы в нештрихованной системе координат.
Преобразования Лоренца:
x =
x
0
+ V t
0
q
1 −
V
2
c
2
y = y
0
z = z
0
t =
t
0
+
V x
0
c
2
q
1 −
V
2
c
2
.
dx =
dx
0
+ V dt
0
q
1 −
V
2
c
2
.
dy = dy
0
.
dz = dz
0
.
dt =
dt
0
+
V
c
2
dx
0
q
1 −
V
2
c
2
.
Рассмотрим ситуацию, когда система координат связана с частицей.
O
0
движется по O со скоростью V .
~v — постоянная скорость движения частицы.
Выбираем систему координат, связанную с частицей.
τ — время в той системе координат, в которой объект покоится.
t =
τ
q
1 −
v
2
c
2
⇒ dτ =
r
1 −
v
2
c
2
dt
t
0
=
τ
q
1 −
v
0
2
c
2
⇒ dτ =
r
1 −
v
0
2
c
2
dt
0
dx
dτ
=
dx
0
dτ
+ V
dt
0
dτ
q
1 −
V
2
c
2
⇒
dx
dt
|{z}
v
x
·
1
q
1 −
v
2
c
2
=
v
0
x
0
z}|{
dx
0
dt
0
·
1
r
1−
v
0
2
c
2
+ V ·
dt
0
dt
0
r
1−
v
0
2
c
2
q
1 −
V
2
c
2
.
^ v
x
·
1
q
1 −
v
2
c
2
=
v
0
x
0
·
1
r
1−
v
0
2
c
2
+ V ·
1
r
1−
v
0
2
c
2
q
1 −
V
2
c
2
× m
0
.
m
0
v
x
q
1 −
v
2
c
2
=
m
0
v
0
x
0
q
1 −
v
0
2
c
2
+
m
0
V
q
1 −
v
0
2
c
2
·
c
2
c
2
·
1 −
V
2
c
2
−
1
2
.
Браницкий А.А. 67 M∀TM∃X 2012
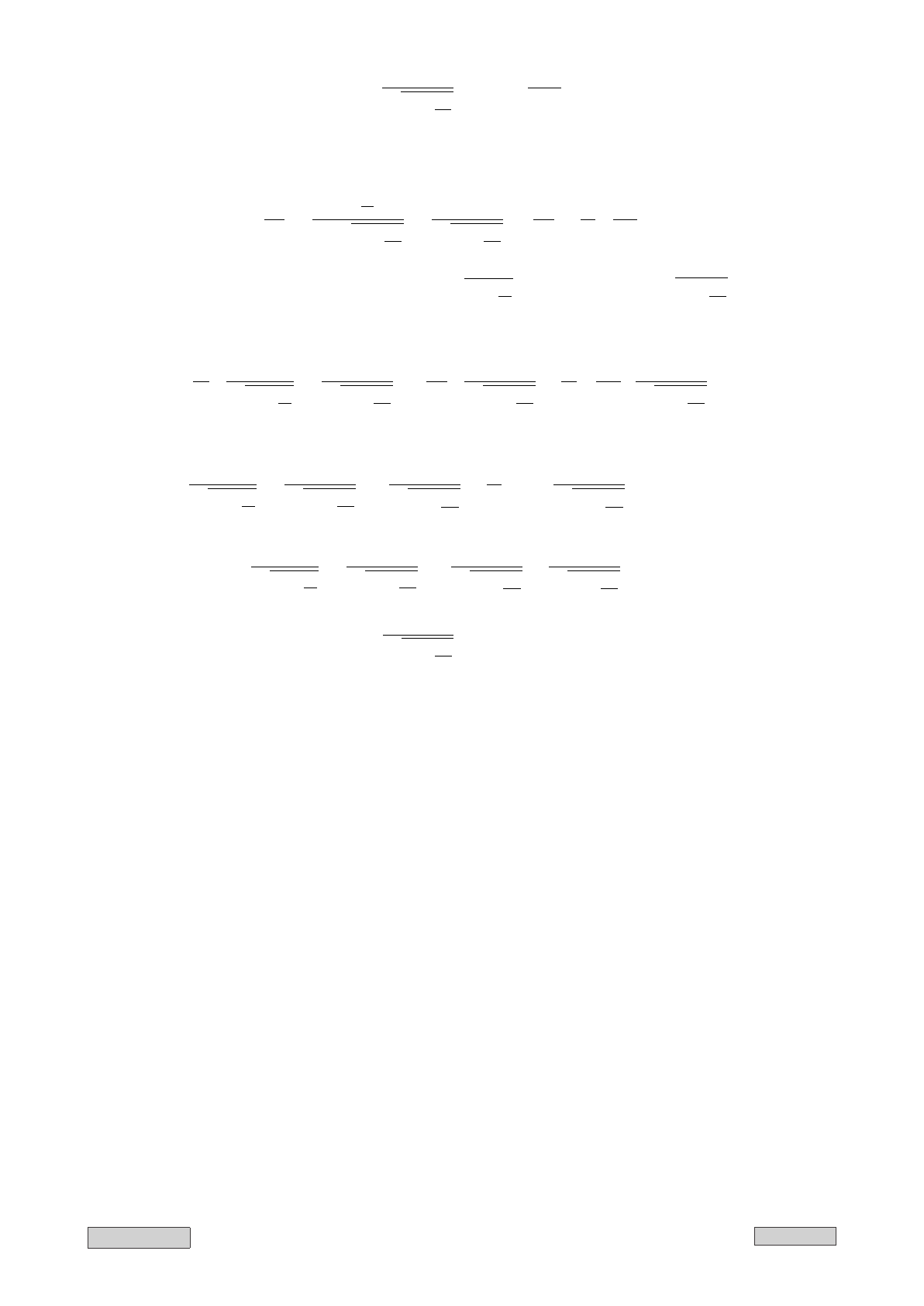
p
x
=
1
q
1 −
V
2
c
2
·
p
0
x
0
+
V E
0
c
2
. (III.4)
Это выражение представляет собой проекцию импульса в нештрихованной системе ко-
ординат. Т. с. импульс выражается через энергию.
dt
dτ
=
dt
0
+
V
c
2
dx
0
dτ
q
1 −
V
2
c
2
=
1
q
1 −
V
2
c
2
·
dt
0
dτ
+
V
c
2
·
dx
0
dτ
.
Подставив в это выражение слева dτ =
q
1 −
v
2
c
2
dt и справа dτ =
q
1 −
v
0
2
c
2
dt
0
, получим:
dt
dt
·
1
q
1 −
v
2
c
2
=
1
q
1 −
V
2
c
2
·
dt
0
dt
0
·
1
q
1 −
v
0
2
c
2
+
V
c
2
·
dx
0
dt
0
|{z}
v
0
x
0
·
1
q
1 −
v
0
2
c
2
.
1
q
1 −
v
2
c
2
=
1
q
1 −
V
2
c
2
·
1
q
1 −
v
0
2
c
2
+
V
c
2
· v
0
x
0
·
1
q
1 −
v
0
2
c
2
× m
0
c
2
.
m
0
c
2
q
1 −
v
2
c
2
=
1
q
1 −
V
2
c
2
·
m
0
c
2
q
1 −
v
0
2
c
2
+
m
0
v
0
x
0
q
1 −
v
0
2
c
2
· V
.
E =
1
q
1 −
V
2
c
2
· (E
0
+ p
0
x
0
· V ) . (III.5)
Импульс и энергия выступают как единое целое.
Выражения III.4 и III.5 показывают, что импульс и энергия изменяются вместе. В
какой-то системе может быть импульс и не быть энергии, а в другой системе для того же
объекта — наоборот.
Браницкий А.А. 68 M∀TM∃X 2012

Глава IV
Элементы векторного анализа
IV.1 Векторное и скалярное поля
IV.1.1 Основные понятия векторного анализа
Векторное поле: ~a = ~a(
~
R). Скалярное поле: ϕ = ϕ(
~
R).
1
~
R
0
(·)P
0
-
~
R
(·)P
A
A
A
AU
∆
~
l
Рис. IV.1: Вектор элементарных пе-
ремещений ∆
~
l
Векторное поле — это поле скоростей.
Скалярное поле — это поле температур.
Устремляя вектор
~
R к вектору
~
R
0
, получаем вектор
элементарных перемещений d
~
l (см. рис. IV.1).
Производная от скалярного поля по направлению
∂ϕ
∂
~
l
|
P
0
lim
|∆
~
l|→0
ϕ(
~
R) − ϕ(
~
R
0
)
|∆
~
l|
.
Она зависит от точки и от направления.
-
x
6
y
z
ϕ = const
0
Рис. IV.2: Эквипотенциальная по-
верхность
Уравнение ϕ(
~
R) = const задает эквипотенциальную
поверхность, или поверхность равного уровня (см.
рис. IV.2).
Эквипотенциальную поверхность можно интерпре-
тировать как изотермическую поверхность (поверх-
ность, на которой температура постоянна).
&%
'$
~n
Рис. IV.3: Замкнутая поверхность
В любой точке поверхности положительная и отри-
цательная нормаль взаимно противоположны.
Если поверхность замкнутая (см. рис. IV.3), то поло-
жительное направление нормали — это направление
наружу. Нормаль всегда представляет собой единич-
ный вектор.
9
-
6
~n
Рис. IV.4: Незамкнутая поверхность
Если поверхность незамкнутая (см. рис. IV.4), то по-
ложительное направление нормали определяют по
правилу Буравчика (правилу правой руки).
Если обхода контура нет, то обход произвольный, но
с добавлением положительного обхода контура.
69

Рассмотрим разрез поверхности:
• нет обхода;
• ∆ϕ > 0.
Строим эквипотенциальные поверхности (см. рис. IV.5).
Положительное направление нормали будет определяться в сторону роста значений
эквипотенциальных поверхностей.
ϕ = ϕ
0
+ ∆ϕ
ϕ = ϕ
0
~n
∆~n
*
~
l
∆
~
l
P
0
P
n
P
Рис. IV.5: Эквипотенциальные по-
верхности
~
l — произвольное направление.
P
0
— пересечение ~n с ближайшей эквипотенциальной
поверхностью.
∆~n — вектор единичной нормали.
ϕ(
~
R) = ϕ(
~
R
n
).
P
n
— вектор, совпадающий по направлению с нор-
малью и по модулю равный расстоянию от точки P
0
до точки P
n
.
|∆~n| = |∆
~
l| · cos(
~
l, ~n) (если ∆ϕ мало).
∂ϕ
∂
~
l
= lim
|∆
~
l|→0
ϕ(
~
R) − ϕ(
~
R
0
)
|∆
~
l|
= lim
|∆~n|→0
ϕ(
~
R
n
) − ϕ(
~
R
0
)
|∆~n|
· cos(
~
l, ~n) =
∂ϕ
∂~n
· cos(
~
l, ~n).
Градиент: gradϕ
∂ϕ
∂~n
·~n, где ~n — единичный вектор нормали.
∂ϕ
∂
~
l
|
P
0
= (gradϕ)
~
l
| {z }
проекция
градиента на
направление
~
l
|
P
0
.
-
x
-
~
i
6
y
6
~
j
z
~
k
0
Рис. IV.6: Декартова система коор-
динат
Рассмотрим декартову систему координат (см. рис.
IV.6).
Единичные орты
~
i,
~
j,
~
k образуют правую тройку век-
торов.
(gradϕ)
x
=
∂ϕ
∂
~
i
=
∂ϕ
∂x
,
(gradϕ)
y
=
∂ϕ
∂
~
j
=
∂ϕ
∂y
,
(gradϕ)
z
=
∂ϕ
∂
~
k
=
∂ϕ
∂z
.
gradϕ =
∂ϕ
∂x
,
∂ϕ
∂y
,
∂ϕ
∂z
— это равенство можно брать
за определение градиента (оно не является строгим,
поскольку привязано к системе координат).
Производная от векторного поля по направлению:
∂~a
∂
~
l
lim
|∆
~
l|→0
~a(
~
R) −~a(
~
R
0
)
|∆
~
l|
.
Приращение векторного поля между точками
~
R и
~
R
0
:
~a(
~
R) −~a(
~
R
0
) = ∆~a.
Браницкий А.А. 70 M∀TM∃X 2012
