Волков А.А. Курс физики
Подождите немного. Документ загружается.

~
P =
~p
R
=
~p
0
· f
t −
R
c
R
= ~p
0
· Φ(t, R), ~p
0
— постоянный вектор.
rot
~
P = rot(~p
0
· Φ) = [gradΦ, ~p
0
] =
∂Φ
∂R
· gradR, ~p
0
=
1
R
∂Φ
∂R
[
~
R, ~p
0
].
-
y
6
z
x
0
R
меридиан
(долгота)
параллель
(широта)
α
Θ
@
@R~e
Θ
9
~e
α
~e
R
(·)
6
~p
0
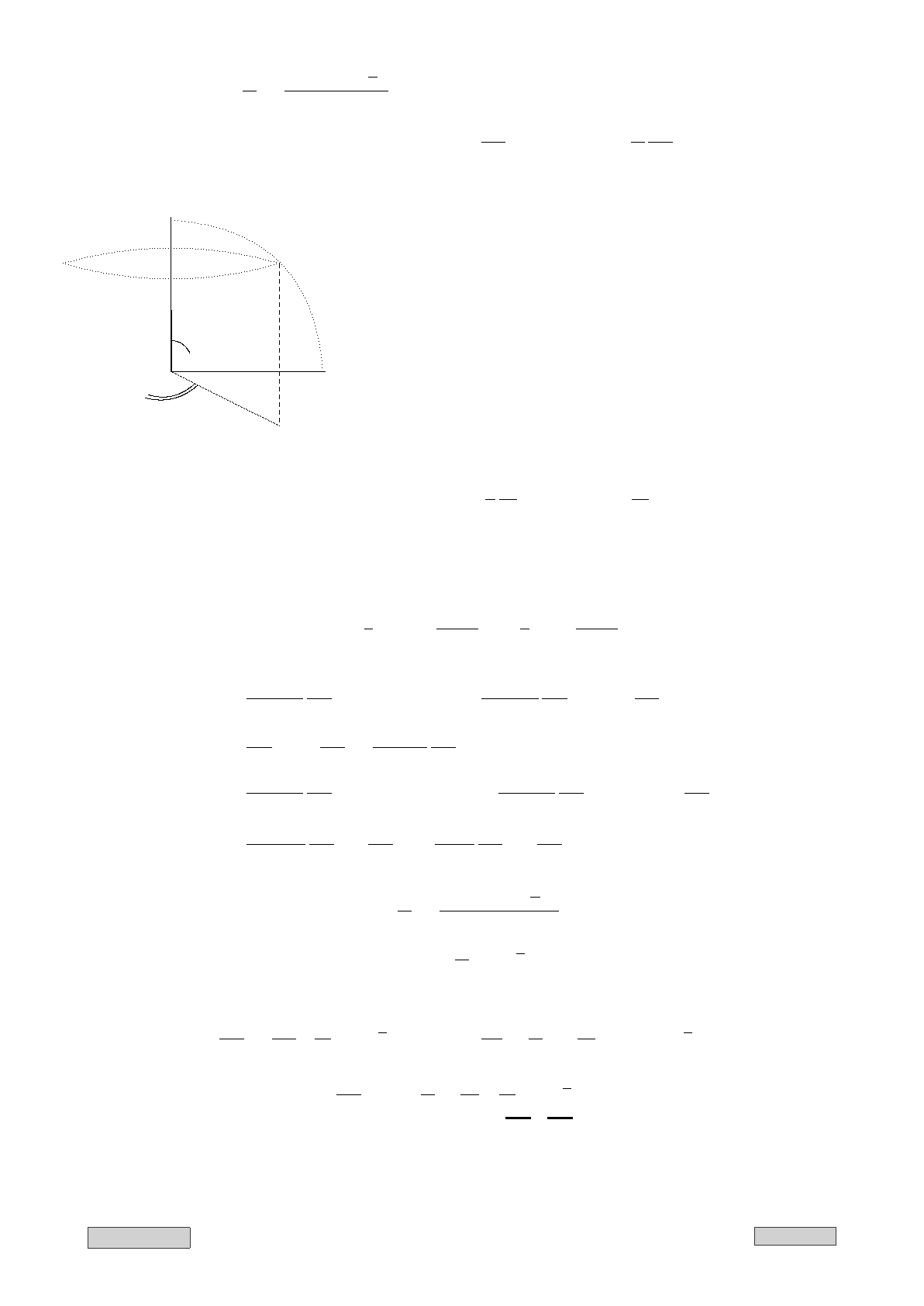
Рис. II.10: Сферическая система ко-
ординат
Введем сферическую систему координат (см. рис.
II.10).
α — угол в плане.
(·) — точка, в которой производится наблюдение.
(R, Θ, α).
Координатная линия — меняется только один пара-
метр.
При изменении Θ координатная линия — долгота.
При изменении α координатная линия — широта.
(Касательная к широте) ⊥ (касательная к долготе).
Рассмотрим проекции:
[rot
~
P ]
R
= 0.
[rot
~
P ]
Θ
= 0.
[rot
~
P ]
α
=
1
R
∂Φ
∂R
R · p
0
sin Θ =
∂Φ
∂R
p
0
sin Θ.
H
R
= 0.
H
Θ
= 0.
H
α
= −
1
c
p
0
sin Θ
∂
2
Φ
∂R∂t
= −
1
c
sin Θ
∂
2
P
∂t∂R
.
E
R
=
1
R sin Θ
∂
∂Θ
sin Θ[rot
~
P ]
α
=
p
0
R sin Θ
∂
∂Θ
sin
2
Θ
∂Φ
∂R
=
2p
0
R
cos Θ
∂Φ
∂R
=
2 cos Θ
R
∂P
∂R
.
E
Θ
=
1
R sin Θ
∂
∂R
R sin Θ[rot
~
P ]
α
=
1
R sin Θ
∂
∂R
R sin
2
Θp
0
∂Φ
∂R
=
p
0
sin Θ
R
∂
∂R
R
∂Φ
∂R
=
sin Θ
R
∂
∂R
R
∂P
∂R
.
Φ =
f
R
=
cos
ω
t −
R
c
R
.
~
P = ~p
0
·
1
R
e
iω
(
t−
R
c
)
.
p
0
Φ = P.
∂P
∂R
=
∂
∂R
p
0
R
e
iω
(
t−
R
c
)
= p
0
−
1
R
2
+
1
R
−
iω
c
· e
iω
(
t−
R
c
)
.
∂P
∂R
= −
1
R
+
iω
c
p
0
R
e
iω
(
t−
R
c
)
| {z }
P
.
Браницкий А.А. 51 M∀TM∃X 2012

∂
∂R
R
∂P
∂R
= −
∂
∂R
1 +
iω
c
R
P
= −
iω
c
P +
1 +
iω
c
R
·
1
R
+
iω
c
P =
−
iω
c
+
1
R
+
iω
c
+
iω
c
−
ω
2
c
2
R
P =
1
R
+
iω
c
−
ω
2
c
2
R
P.
H
α
=
1
c
sin Θ
1
R
+
iω
c
∂P
∂t
=
1
c
sin Θ
1
R
+
iω
c
iωP.
E
R
= −
2 cos Θ
R
·
1
R
+
iω
c
P.
E
Θ
=
sin Θ
R
·
1
R
+
iω
c
−
ω
2
c
2
R
P.
II.3 Теорема Умова-Пойнтинга. Вектор Пойнтинга. Ба-
ланс электромагнитной энергии
II.3.1 Теорема Умова-Пойнтинга
Теорема 1 (Умов-Пойнтинг). Энергия электромагнитного поля, сосредоточенного в об-
ласти V , равна
W =
1
8π
Z
V
~
E ·
~
D +
~
H ·
~
B
dV.
Доказательство. Плотность энергии: w
1
8π
~
E ·
~
D +
~
H ·
~
B
.
W =
Z
V
wdV.
∂W
∂t
=
Z
V
∂w
∂t
dV.
Будем считать, что среда такая, что ε, µ не зависят от времени.
~
D = ε
~
E.
~
B = µ
~
H.
w =
1
8π
ε
~
E
2
+ µ
~
H
2
.
∂w
∂t
=
1
4π
ε
~
E
∂
~
E
∂t
+ µ
~
H
∂
~
H
∂t
!
=
1
4π
~
E
∂
~
D
∂t
+
~
H
∂
~
B
∂t
!
.
rot
~
E = −
1
c
∂
~
B
∂t
⇒
∂
~
B
∂t
= −c · rot
~
E.
rot
~
H =
4π
c
~
j +
1
c
∂
~
D
∂t
⇒
∂
~
D
∂t
=
rot
~
H −
4π
c
~
j
· c = −4π
~
j + c · rot
~
H.
∂w
∂t
=
1
4π
−4π
~
j
~
E + c ·
~
Erot
~
H − c ·
~
Hrot
~
E
= −
~
j
~
E +
c
4π
~
Erot
~
H −
~
Hrot
~
E
=
−
~
j
~
E −
c
4π
div[
~
E,
~
H].
Браницкий А.А. 52 M∀TM∃X 2012
∂W
∂t
= −
Z
V
~
j
~
EdV −
c
4π
Z
V
div[
~
E,
~
H]dV = −
Z
V
~
j
~
EdV −
c
4π
I
S
[
~
E,
~
H]d~s.
1. Предполагается: V столь большой, что все поле заключено внутри ⇒
H
S
[
~
E,
~
H]d~s = 0.
∂W
∂t
= −
Z
V
~
j
~
EdV.
Это уравнение означает, что при предполагаемой неподвижности всех находящихся
в поле материальных тел энергия поля W расходуется только на работу, совершаемую
электрическим полем
~
E над токами проводимости
~
j [3, стр. 347].
~
j = e
~
v
0
,
где e — заряд одной частицы;
~
v
0
— средняя скорость (скорость на единицу объема).
Сила Лоренца в вакууме (действует на заряд, помещенный в электромагнитное поле):
~
F e
~
E +
1
c
[~v,
~
H]
.
Импульс: ~p = m~v.
Второй закон Ньютона:
d
~
p
0
dt
=
~
F = e
~
E +
1
c
[
~
v
0
,
~
H]
.
~
v
0
d
~
p
0
dt
= e
~
v
0
~
E +
e
c
~
v
0
[
~
v
0
,
~
H]
| {z }
0
=
~
j
~
E.
Кинетическая энергия: E =
mv
2
2
.
dE
dt
=
d
dt
mv
0
2
2
=
d
dt
~
v
0
~
p
0
2
!
=
~
v
0
d
~
p
0
dt
=
~
j
~
E.
∂W
∂t
|{z}
R
V
∂w
∂t
dV
= −
Z
V
~
j
~
EdV = −
Z
V
dE
dt
dV.
Z
V
∂w
∂t
+
dE
dt
dV = 0.
Закон сохранения заряда:
∂
∂t
Z
V
(w + E )dV
= 0.
2. V — не столь большая область. Есть перенос и частиц, и электромагнитного поля
через границу.
Z
V
∂w
∂t
dV = −
Z
V
~
j
~
EdV −
c
4π
I
S
[
~
E,
~
H]d~s ⇒
Z
V
∂w
∂t
+
dE
dt
dV = −
I
S
c
4π
[
~
E,
~
H]
| {z }
~
S
d~s.
A переносится только поле.
Левая часть — изменение энергии внутри объема.
Правая часть — поток электромагнитного поля через поверхность.
”
−“ — вынос электромагнитного поля, энергия уменьшается.
Браницкий А.А. 53 M∀TM∃X 2012

II.3.2 Вектор Пойнтинга
Вектор Пойнтинга:
~
S
c
4π
[
~
E,
~
H].
~
S — плотность потока энергии.
II.3.3 Закон сохранения энергии
Закон сохранения энергии: общее приращение электромагнитной энергии (при предпо-
лагаемой неподвижности материальных тел) равно избытку работы сторонних электро-
движущих сил (химического, термического и тому подобного происхождения) над выде-
лением джоулева тепла (все тела неподвижны, так что механическая работа равна нулю)
[3, стр. 347].
Браницкий А.А. 54 M∀TM∃X 2012
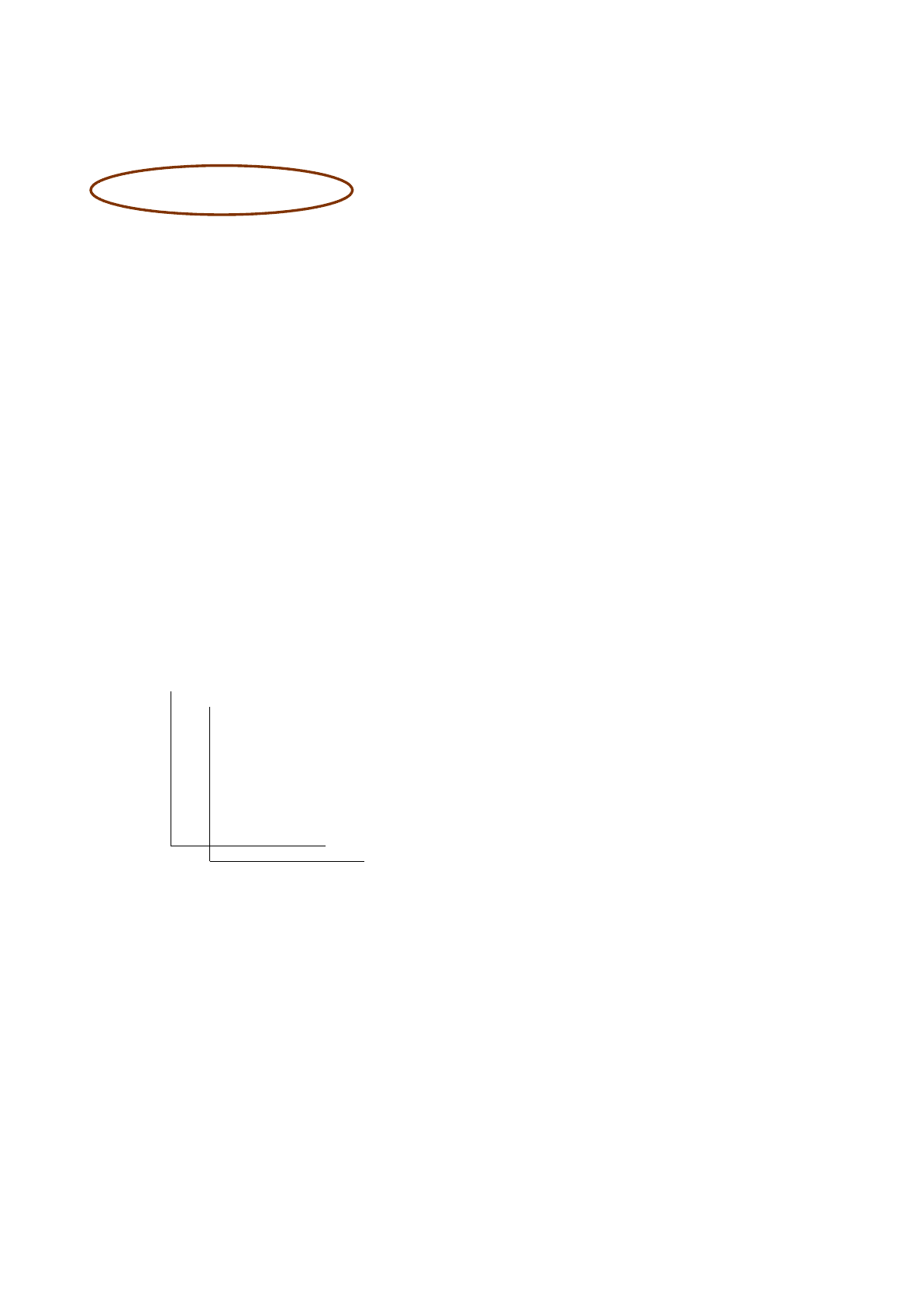
Глава III
Теория относительности
III.1 Элементы теории относительности. Преобразова-
ния Лоренца и следствия из них
III.1.1 Закон сложения скоростей в классической теории
Всякое явление рассматривается в какой-то системе отсчета.
Инерциальные системы отсчета — такие системы, что при отсутствии сил, действую-
щих на тело, оно движется равномерно и прямолинейно (скорость = 0 — частный случай).
Равномерное и прямолинейное движение легче всего рассматривать в декартовой си-
стеме координат.
Принцип относительности (формулировка Галилея): равномерное и прямолинейное
движение изолированной не влияет на ход процессов внутри нее.
Рассмотрим иллюстрацию этого принципа.
-
x
0
6
y
0
z
0
0
0
-
x
6
y
z
0
Рис. III.1: Cистемы отсчета
Есть некоторая изолированная система, с ней связа-
на какая-то инерциальная система отсчета (см. рис.
III.1). Есть другая система отсчета, которая движет-
ся равномерно и прямолинейно вдоль Ox со скоро-
стью V .
В какой-то момент центры 0 и 0
0
соединяются.
Процессы в системе и ее клоне будут одинаковые.
Наблюдатель ассоциирован с нештрихованной си-
стемой координат.
Время в обоих системах течет одинаково.
Масштаб не меняется при движении.
x = x
0
+ V t
0
y = y
0
z = z
0
— преобразование Галилея.
Принцип относительности является постулатом (т. е. не требует доказательства); под-
тверждается всей совокупностью существующих фактов.
Как соотносится преобразование Галилея с принципом относительности?
Ускорение: ~w.
55

Мы рассматриваем равномерное движение (V = const) ⇒ ускорение равно нулю.
m ~w = m
d
2
~r
dt
2
= m
d~v
dt
=
~
F .
m
d
2
x
dt
2
= m
d
2
(x
0
+ V t
0
)
dt
0
2
= m
d( ˙x
0
+ V )
dt
0
= m
d
2
x
0
dt
0
+ m
dV
dt
0
|{z}
w=0
= mw
0
x
= F
x
.
m
d
2
y
dt
2
= m
d
2
y
0
dt
0
2
= mw
0
y
= F
y
.
m
d
2
z
dt
2
= m
d
2
z
0
dt
0
2
= mw
0
z
= F
z
.
Т. с. форма 2-ого закона Ньютона не меняется.
~v = (v
x
, v
y
, v
z
) = ( ˙x, ˙y, ˙z).
v
x
=
dx
dt
=
d(x
0
+ V t
0
)
dt
0
= ˙x
0
+ V = v
0
x
0
+ V.
v
y
=
dy
dt
=
dy
0
dt
0
= v
0
y
0
.
v
z
=
dz
dt
=
dz
0
dt
0
= v
0
z
0
.
~v =
~
v
0
+
~
V — закон сложения скоростей.
В уравнения Максвелла входит постоянная величина c, имеющая размерность скорости
[1, стр. 139].
Покажем, что c совпадает со скоростью распространения электромагнитных волн в
пустом пространстве.
Запишем систему уравнений Максвелла в вакууме:
rot
~
E = −
1
c
∂
~
H
∂t
∂
∂t
⇒ rot
∂
~
E
∂t
!
= −
1
c
∂
2
~
H
∂t
2
div
~
H = 0.
rot
~
H =
1
c
∂
~
E
∂t
rot
⇒ rot(rot
~
H)
| {z }
grad( div
~
H
|{z}
0
)−∆
~
H
=
1
c
rot
∂
~
E
∂t
!
div
~
E = 0.
Отсюда получаем:
−∆
~
H = −
1
c
2
∂
2
~
H
∂t
2
.
∆
~
H −
1
c
2
∂
2
~
H
∂t
2
= 0 —
волновое уравнение; решением является
бегущая волна со скоростью распространения c.
Т. е. v = c явно входит в уравнения Максвелла.
Браницкий А.А. 56 M∀TM∃X 2012
III.1.2 Опыт Майкелсона
Был произведен прямой опыт, показавший справедливость того, что скорость света и
вообще всякого электромагнитного возмущения в вакууме не складывается со скоростью
системы отсчета. Во всех направлениях скорость света в любой инерциальной системе
отсчета равна одной и той же фундаментальной величине c. Этот опыт выполнил в 1887 г.
Майкелсон. Опишем опыт вкратце [1, стр. 140].
- -
?
6
6
S
S
A
C
B
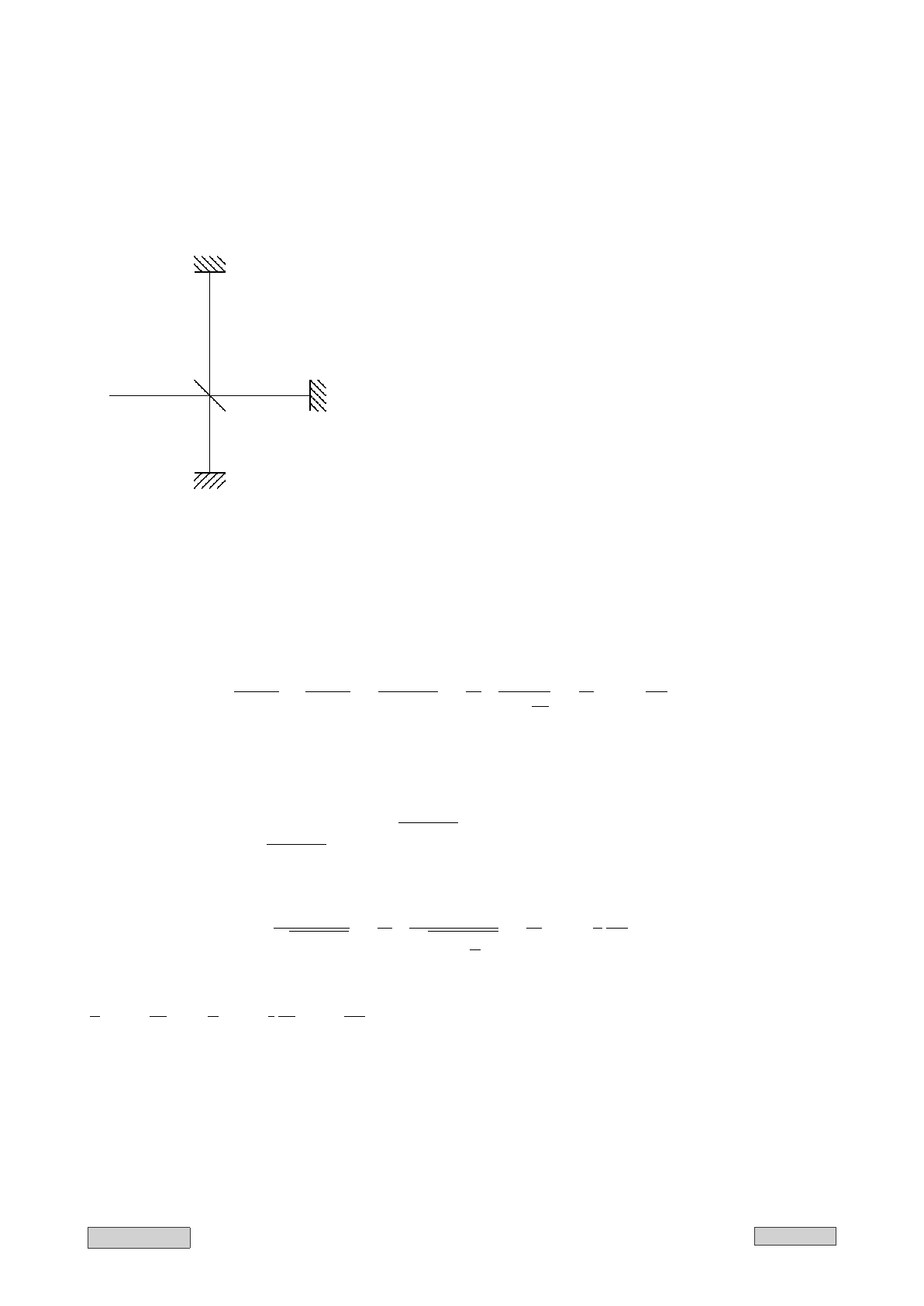
Рис. III.2: Опыт Майкелсона
Луч света падает на полупосеребренную пластинку
SS (см. рис. III.2). При этом он раздваивается: часть
света отражается и падает на зеркало A, а часть
проходит и падает на зеркало B. Пусть луч SA пер-
пендикулярен скорости Земли в ее движении вокруг
Солнца, а луч SB параллелен той же скорости. От-
раженный от зеркал A и B свет возвращается на
пластинку SS: луч BS отражается от нее и попада-
ет на экран C, а луч AS проходит через SS прямо и
падает на экран C. Поэтому оба луча в отношении
прохождений и отражений совершенно равноценны,
но на участках AS и BS свет распространяется раз-
лично относительно движения Земли [1, стр. 140].
Посмотрим, какого эффекта следовало бы ожидать, если бы скорость света склады-
валась со скоростью движения Земли по обычному закону. На пути SB скорость света
относительно Земли равнялась бы c − V , а на обратном пути c + V , где V — скорость
Земли. Время прохождения светом всего пути SBS в обе стороны равно в сделанном
предположении [1, стр. 141]:
l
c + V
+
l
c − V
=
2lc
c
2
− V
2
=
2l
c
·
1
1 −
V
2
c
2
≈
2l
c
1 +
V
2
c
2
,
где l = SB. Переходя к приближенному равенству мы воспользовались тем, что V c.
На участке SA скорости Земли и света перпендикулярны (в системе отсчета, связан-
ной с прибором). Допуская снова, что скорость света складывается со скоростью Земли,
надо на этот раз применить векторный закон сложения. Тогда на участке SA скорость
света относительно прибора равна
√
c
2
− V
2
, потому что c — гипотенуза прямоугольного
треугольника, V и
√
c
2
− V
2
— его катеты. Время прохождения светом всего пути SAS,
равного 2l, есть [1, стр. 141]:
2l
√
c
2
− V
2
=
2l
c
·
1
q
1 −
V
c
2
≈
2l
c
1 +
1
2
V
2
c
2
.
Таким образом, разность времен прохождения светом путей SBS и SAS равна
2l
c
1 +
V
2
c
2
−
2l
c
1 +
1
2
V
2
c
2
=
lV
2
c
3
. С помощью многократных отражений путь делается
довольно длинным (десятки метров). Выбирая его надлежащим образом, можно добиться
того, что предполагаемая разность времен прохождения путей SAS и SBS станет рав-
на полупериоду световых колебаний. Тогда если все рассуждение было верным, лучи на
экране должны погаситься [1, стр. 141].
Чтобы убедиться в том, что гашение лучей в данной точке экрана произошло именно
вследствие сложения скоростей Земли и световых лучей, достаточно повернуть прибор
на 45
◦
так, чтобы скорость Земли стала направленной по биссектрисе угла ASB. При
Браницкий А.А. 57 M∀TM∃X 2012

этом разность времен прохождения лучами путей SAS и SBS должна во всяком случае
стать равной нулю, если в первоначальном положении эта разность составляла полпериода
колебаний. Иными словами, интерференционные полосы на экране должны сместиться
на половину расстояния между двумя полосами: там, где было светлое место на экране,
появится темное, и наоборот [1, стр. 141].
Фактически никакого изменения разности хода лучей от поворота прибора не наблюда-
ется, т. е. ожидавшийся эффект полностью отсутствует. Скорость света не складывается
со скоростью Земли [1, стр. 141].
III.1.3 Преобразования Лоренца
Будем искать преобразования более общего вида, чем преобразования Галилея для
перехода от одной инерциальной системы отсчета к другой. Подобно преобразованиям
Галилея, они должны удовлетворять некоторым требованиям общего характера, которые
перечислены ниже [1, стр. 143]:
1. Формулы перехода должны быть симметричны относительно обеих инерциальных
систем.
Скорость штрихованной системы отсчета относительно нештрихованной равна V .
Тогда прямые формулы перехода должны преобразовываться в обратные при про-
стой замене V на −V . Это требование необходимо для равноправия обеих систем
отсчета.
2. Преобразование должно переводить точки одной системы отсчета, находящиеся на
конечном расстоянии от произвольного начала координат, в точки, тоже находящиеся
на конечном расстоянии от произвольного начала другой системы отсчета.
3. Когда относительная скорость двух систем стремится к нулю, формулы перехода
дают тождество: x = x
0
, y = y
0
, z = z
0
, t = t
0
.
4. Из формул преобразования следует такой закон сложения скоростей, который остав-
ляет скорость света в пустоте инвариантной.
Преобразования Лоренца:
x =
x
0
+ V t
0
q
1 −
V
2
c
2
y = y
0
z = z
0
t =
t
0
+
V x
0
c
2
q
1 −
V
2
c
2
.
Обратные формулы имеют вид:
x
0
=
x − V t
q
1 −
V
2
c
2
y
0
= y
z
0
= z
t
0
=
t −
V x
c
2
q
1 −
V
2
c
2
.
Браницкий А.А. 58 M∀TM∃X 2012

Пусть в начале координат x
0
= 0 штрихованной системы покоятся часы. Они показы-
вают время t
0
. Тогда [1, стр. 146]:
t =
t
0
q
1 −
V
2
c
2
.
Назовем часами наблюдателя те часы, которые покоятся относительно его системы
отсчета. Отсюда видно, что один наблюдатель, сверяя свои часы, которые показывают
время t, с часами другого наблюдателя, всегда заключает, что последние отстают, т. е.
что t
0
< t. Если часы покоятся в начале координат нештрихованной системы, т. е. в точке
x = 0, то формула перехода имеет вид [1, стр. 146]:
t
0
=
t
q
1 −
V
2
c
2
.
Часы, движущиеся относительно некоторого наблюдателя, отстают от его часов
[1, стр. 146].
В теории относительности не существует единого мирового времени, как в ньютонов-
ской механике. Лучше сказать, что абсолютное время ньютоновской механики есть при-
ближенное понятие, справедливое только при малых относительных скоростях сравни-
ваемых часов. Абсолютность ньютоновского времени давала иногда повод считать его
какой-то доопытной, логической категорией, независимой от движения материи. Но сле-
дует помнить, что в механике Ньютона приближенное понятие абсолютного времени не
ведет к противоречиям, так как там принимается, что взаимодействие происходит на рас-
стоянии мгновенно. Достаточно подставить в формулу t
0
=
t−
V x
c
2
q
1−
V
2
c
2
значение c = ∞, и
получится t = t
0
. В ньютоновской механике действие передавалось на расстояние силами
тяготения [1, стр. 146].
III.1.4 Сложение скоростей в теории относительности
v
x
=
dx
dt
=
dx
0
+ V dt
0
dt
0
+
V
c
2
dx
0
=
dx
0
+ V dt
0
dt
0
+
V
c
2
dx
0
·
dt
0
dt
0
=
dx
0
dt
0
+ V
1 +
V
c
2
dx
0
dt
0
=
v
0
x
0
+ V
1 +
V
c
2
v
0
x
0
. (III.1)
dx =
dx
0
+ V dt
0
q
1 −
V
2
c
2
.
dy = dy
0
.
dz = dz
0
.
dt =
dt
0
+
V
c
2
dx
0
q
1 −
V
2
c
2
.
v
y
=
dy
dt
=
dy
0
q
1 −
V
2
c
2
dt
0
+
V
c
2
dx
0
=
dy
0
q
1 −
V
2
c
2
dt
0
+
V
c
2
dx
0
·
dt
0
dt
0
=
dy
0
dt
0
q
1 −
V
2
c
2
1 +
V
c
2
dx
0
dt
0
=
v
0
y
0
q
1 −
V
2
c
2
1 +
V
c
2
v
0
x
0
. (III.2)
v
z
=
dz
dt
=
dz
0
q
1 −
V
2
c
2
dt
0
+
V
c
2
dx
0
=
dz
0
q
1 −
V
2
c
2
dt
0
+
V
c
2
dx
0
·
dt
0
dt
0
=
dz
0
dt
0
q
1 −
V
2
c
2
1 +
V
c
2
dx
0
dt
0
=
v
0
z
0
q
1 −
V
2
c
2
1 +
V
c
2
v
0
x
0
. (III.3)
Браницкий А.А. 59 M∀TM∃X 2012

При малых скоростях формулы III.1, III.2 и III.3 переходят в обычные формулы сло-
жения скоростей. Это видно если формально считать c → ∞, т. е. положить
V
c
= 0. Легко
сообразить, что если v
0
=
q
v
0
x
0
2
+ v
0
y
0
2
+ v
0
z
0
2
= c, то и v = c, т. е. абсолютная величина
скорости электромагнитных возмущений не меняется при переходе от одной системы к
другой.
v
0
2
= v
0
x
0
2
+ v
0
y
0
2
+ v
0
z
0
2
= c
2
.
v
2
= v
2
x
+ v
2
y
+ v
2
z
=
(v
0
x
0
+ V )
2
1 +
V
c
2
v
0
x
0
2
+
v
0
y
0
2
+ v
0
z
0
2
1 −
V
2
c
2
1 +
V
c
2
v
0
x
0
2
=
(v
0
x
0
+ V )
2
1 +
V
c
2
v
0
x
0
2
+
c
2
− v
0
x
0
2
1 −
V
2
c
2
1 +
V
c
2
v
0
x
0
2
=
v
0
x
0
2
+ 2v
0
x
0
V + V
2
+ c
2
− V
2
− v
0
x
0
2
+
V
2
c
2
v
0
x
0
2
1 +
V
c
2
v
0
x
0
2
=
c
2
+ 2v
0
x
0
V +
V
2
c
2
v
0
x
0
2
1 +
V
c
2
v
0
x
0
2
=
c
2
1 +
V
c
2
v
0
x
0
2
1 +
V
c
2
v
0
x
0
2
= c
2
.
Но отдельные проекции скорости света, которые меньше c, конечно, могут меняться,
как и направление светового луча относительно разных наблюдателей, так как абсолют-
ного направления в пространстве нет [1, стр. 148].
III.1.5 Эффект Допплера
В моменты времени t
n
часы в точке 0
0
испускают вспышки.
τ — период появления вспышки.
Наблюдатель света фиксирует вспышки из точки 0
0
в моменты времени t
∗
n
.
t
∗
n
= t
n
+
x
n
c
= t
n
+
V t
n
c
=
1 +
V
c
t
n
.
t
n
=
t
0
n
q
1 −
V
2
c
2
⇒ ∆t
n
=
∆t
0
n
q
1 −
V
2
c
2
=
τ
q
1 −
V
2
c
2
⇒ ∆t
0
n
= τ ⇒ ∆t
n
> τ.
Движущиеся часы замедляются.
∆t
∗
n
=
1 +
V
c
· ∆t
n
=
1 +
V
c
·
τ
1 −
V
2
c
2
=
q
1 +
V
c
1 −
V
c
· τ =
r
c + V
c − V
· τ.
V > 0, движение влево, источник удаляется ⇒ ∆t
∗
n
> τ , красное смещение.
V < 0, движение вправо, источник приближается ⇒ ∆t
∗
n
< τ , фиолетовое смещение.
III.1.6 Вычисление длины движущегося отрезка
l
0
— длина неподвижного отрезка.
l
0
— длина движущегося отрезка.
x
1
= a, x
2
= b, b > a.
l
0
= b − a = x
2
− x
1
.
l
0
= x
0
2
− x
0
1
.
Браницкий А.А. 60 M∀TM∃X 2012
