Волков А.А. Курс физики
Подождите немного. Документ загружается.

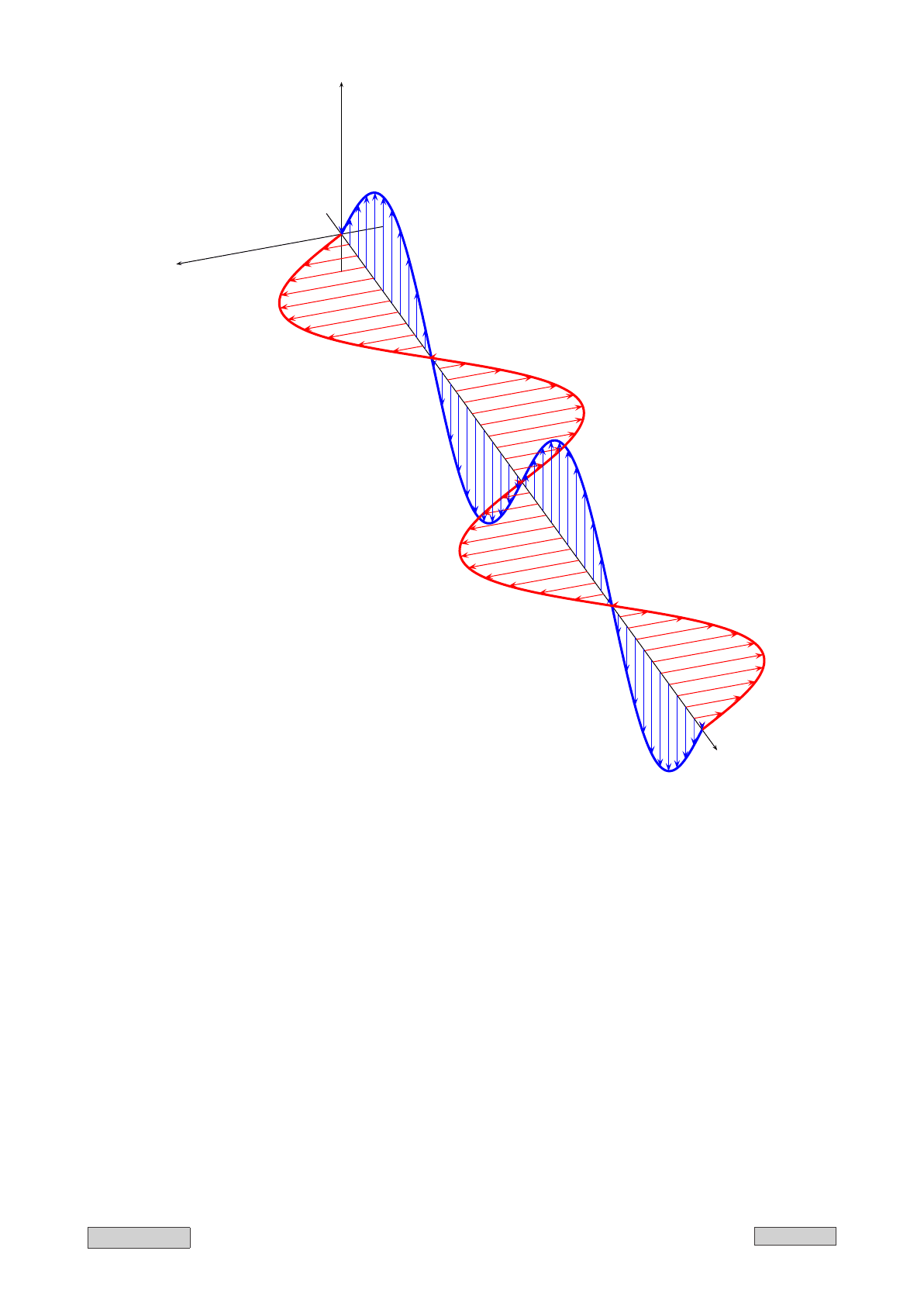
x
y
z
~
E
~
H
Рис. II.2: Линейная поляризация
Браницкий А.А. 41 M∀TM∃X 2012
E
P
= E
1
+ E
2
= E
0
(e
ikx
e
−iωt
+ e
ikx
e
iωt
) = E
0
e
ikx
(e
−iωt
+ e
iωt
) =
E
0
e
ikx
(cos(ωt) − i sin(ωt) + cos(ωt) + i sin(ωt)) =
2E
0
e
ikx
cos(ωt).
Re E
P
= 2E
0
cos(ωt)
| {z }
A(t)
(амплитуда)
cos(kx).
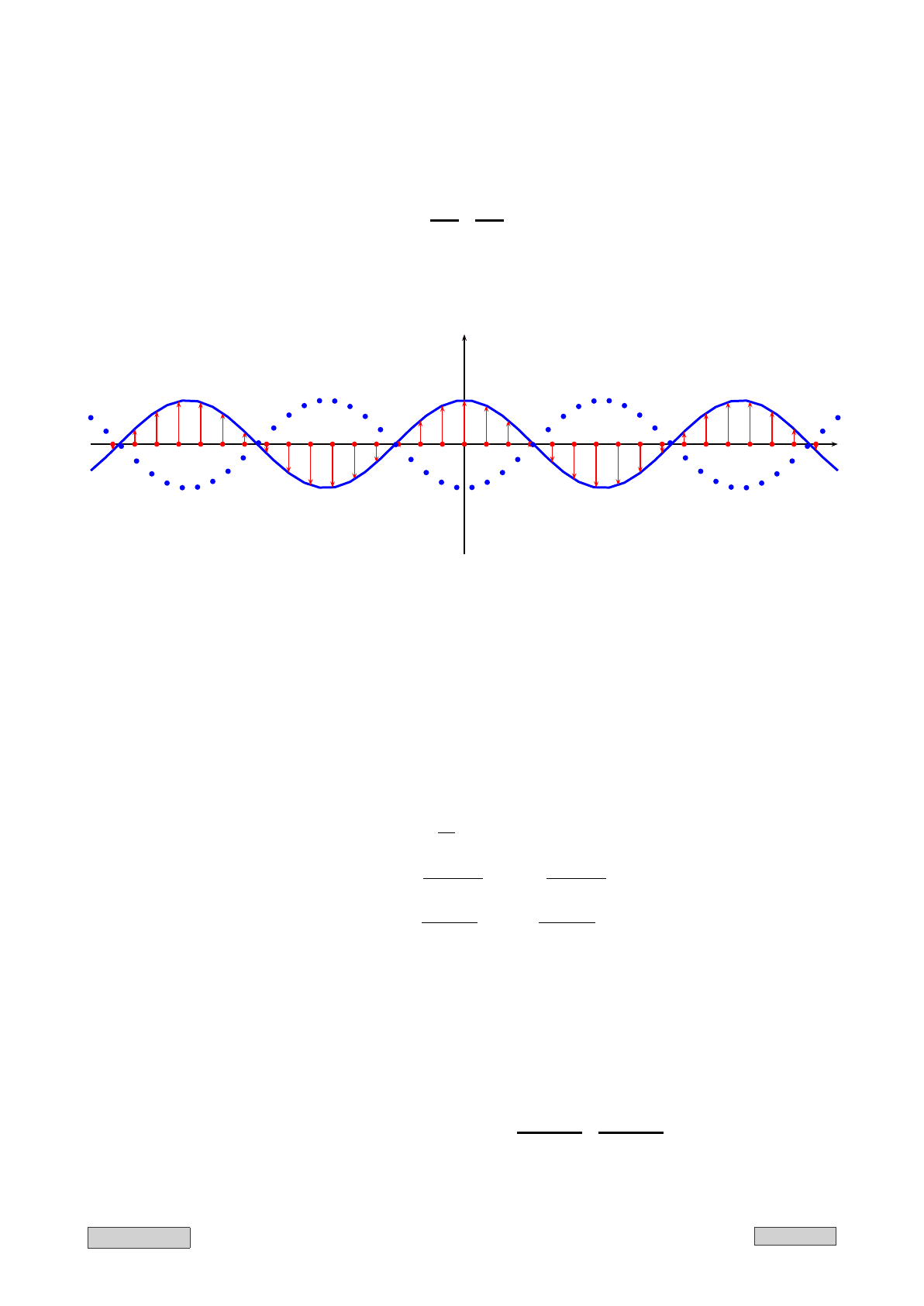
Появляется новый объект — стоячая волна: горизонтальных движений нет (см. рис.
II.3).
x
y
Рис. II.3: Стоячая волна
II.1.6 Сумма двух волн, имеющих одно и то же направление и
разные частоты
E
1
= E
0
· e
i(k
1
x−ω
1
t)
.
E
2
= E
0
· e
i(k
2
x−ω
2
t)
.
ω
2
> ω
1
.
k
i
=
ω
i
c
, i = 1, 2.
Введем: ˜ω =
ω
1
+ ω
2
2
; ∆ω =
ω
2
− ω
1
2
;
˜
k =
k
1
+ k
2
2
; ∆k =
k
2
− k
1
2
.
Отсюда получаем: ω
2
= ˜ω + ∆ω; ω
1
= ˜ω −∆ω;
k
2
=
˜
k + ∆k; k
1
=
˜
k −∆k.
Re E
P
= Re(E
1
+ E
2
) = E
0
Re
e
i(k
1
x−ω
1
t)
+ e
i(k
2
x−ω
2
t)
=
E
0
Re (cos(k
1
x − ω
1
t) + i sin(k
1
x − ω
1
t) + cos(k
2
x − ω
2
t) + i sin(k
2
x − ω
2
t)) =
E
0
Re (cos(k
1
x − ω
1
t) + cos(k
2
x − ω
2
t) + i(sin(k
1
x − ω
1
t) + sin(k
2
x − ω
2
t))) =
E
0
(cos(k
1
x − ω
1
t) + cos(k
2
x − ω
2
t)) = 2E
0
cos(∆kx − ∆ωt)
|
{z }
A(∆kx−∆ωt) —
амплитуда, имеющая
аргумент бегущей волны
(см. рис. II.4)
cos(
˜
kx − ˜ωt).
Браницкий А.А. 42 M∀TM∃X 2012
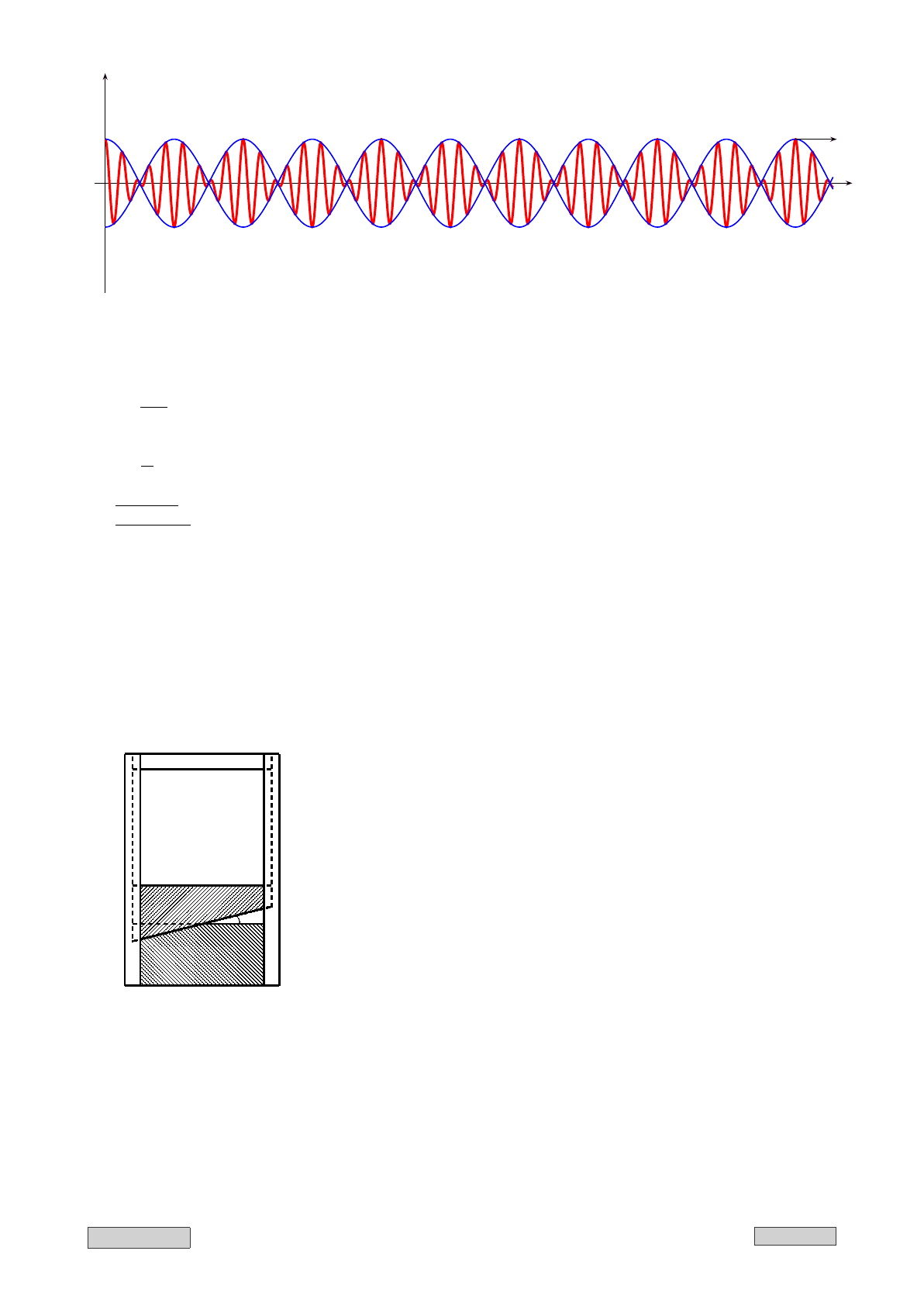
x
y
v
Gr
v
P h
Рис. II.4: Огибающая волна
Скорость волны, задающей амплитуду (групповая скорость абстрактного объекта):
v
Gr
=
∆ω
∆k
= c.
Скорость распространения реального электромагнитного поля (фазовая скорость):
v
P h
=
˜ω
˜
k
= c.
Задача. Посчитать скорость смыкания ножниц Q.
Решение. См. раздел
II.1.7 Эксперимент по передаче информации со сверх-
световой скоростью
.
Волков А.А.:
”
Если считать, что расстояние между концами ножниц больше расстоя-
ния от Земли до Луны, то точка смыкания ножниц движется со скоростью, превышающей
скорость света в 10 раз. В чем парадокс? Парадокс в том, что это абстрактный (нереаль-
ный) объект.“
II.1.7 Эксперимент по передаче информации со сверхсветовой
скоростью
t
B
D
A
D
C
1
C
2
α
Рис. II.5: Гильотинные ножницы
На рис. II.5 показаны так называемые гильотин-
ные ножницы (конструктивно напоминающие из-
вестную гильотину). Нож A с горизонтальной режу-
щей кромкой укреплен неподвижно. Нож B с косой
режущей кромкой поднимается вверх и затем осво-
бождается. Падая по направляющим рейкам C
1
и C
2
нож развивает скорость. Обладая большой массой и
скоростью, он с силой врезается в лист, подлежащий
раскрою [4, стр. 168].
Точка надреза D движется вправо со скоростью тем
большей, чем меньше угол α и чем больше высота, с
которой падает нож. Может ли скорость перемеще-
ния точки надреза в этих ножницах превзойти ско-
рость света [4, стр. 168]?
Пусть нож падает со скоростью 100 м/с и длина режущей кромки ножа составляет 3
км, тогда в этом случае для достижения сверхсветовой скорости правый край падающего
ножа должен быть выше левого не более, чем на 1 мм.
Объясним, почему в данной конструкции точка разреза на полотне, подлежащем рас-
крою, движется со сверхсветовой скоростью. Пусть в момент времени t
0
левый край ножа
Браницкий А.А. 43 M∀TM∃X 2012
находится в точке соприкосновения с полотном, тогда правый край ножа в момент време-
ни t
0
находится на высоте 1 мм от уровня, где находится полотно. По вертикали 1 мм нож
проходит
за
10
−3
м
10
2
м/с
= 10
−5
с. За это же время точка разреза на полотне
успеет
пе-
реместиться слева направо на 3 км. Понятно, что скорость ее перемещения составляет
3·10
3
м
10
−5
с
= 3 · 10
8
м/с.
II.1.8 Немонохроматическая (несущая) волна
-
0
ω
0
−
∆ω
2
ω
0
ω
0
+
∆ω
2
ω
∆ω
@
@
@
@I
достаточно
далеко от 0
Рис. II.6: Частотная ось
E = E
0
0
· e
−i(ωt−kx)
.
E
P
=
ω
0
+
∆ω
2
Z
ω
0
−
∆ω
2
E
0
· e
−i(ωt−kx)
dω.
Плотность амплитуды: E
0
.
Размерная частота: ω (см. рис. II.6).
ω ∈
ω
0
−
∆ω
2
, ω
0
−
∆ω
2
.
ω
0
∆ω, ω
0
—несущая частота.
|ω
0
− ω| 1.
E
P
= E
0
ω
0
+
∆ω
2
Z
ω
0
−
∆ω
2
e
−i(ωt−kx)
dω.
Для вакуума: k =
ω
c
= k(ω).
В общем случае: k =
ω
v
, где v =
c
√
εµ
. Отсюда: k =
ω
c
√
εµ = k(ω).
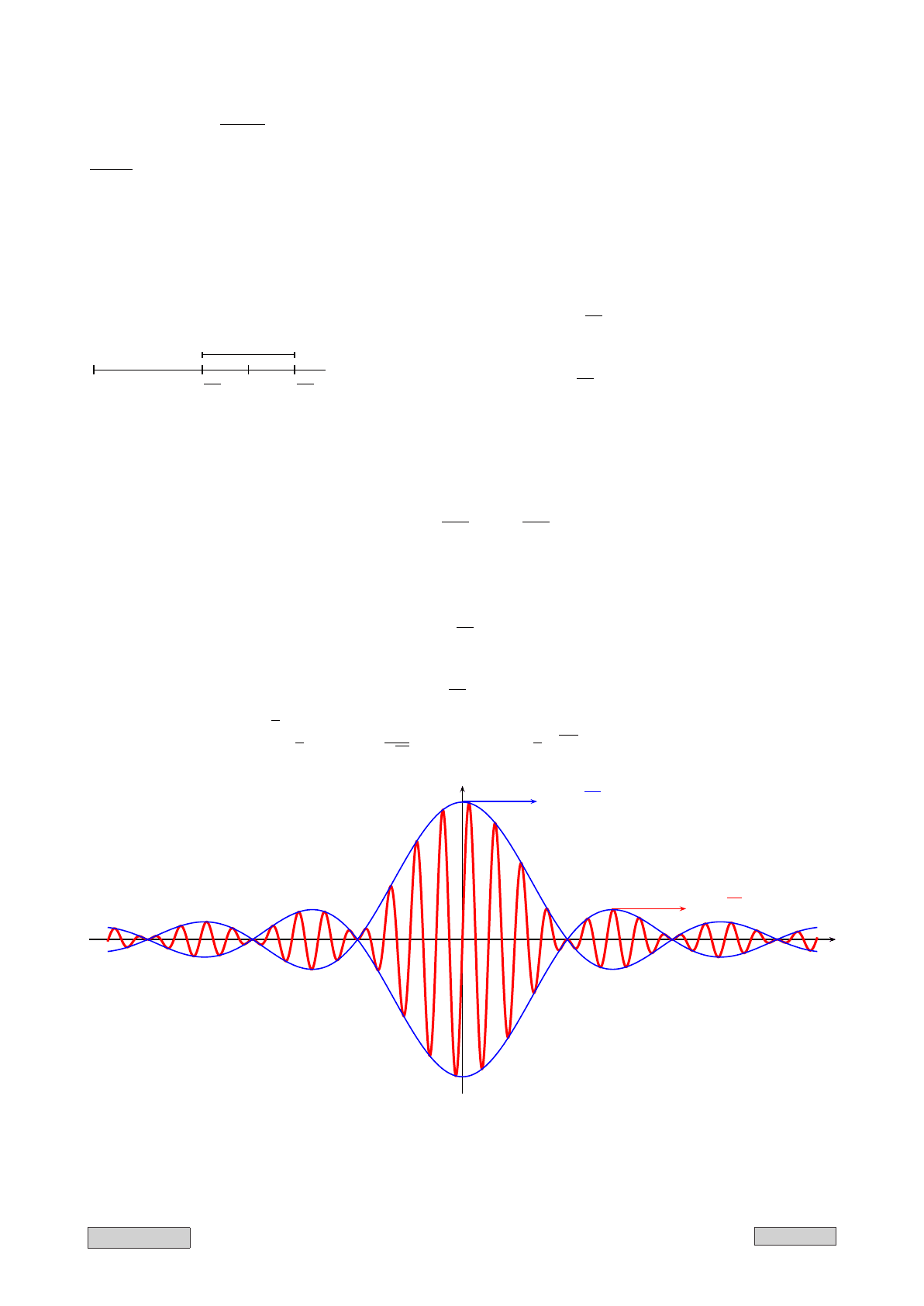
x
y
v
Gr
=
dω
dk
k
0
v
P h
=
ω
0
k
0
Рис. II.7: Затухающая волна
Браницкий А.А. 44 M∀TM∃X 2012
Поскольку рассматриваем точки вблизи ω, то справедливо разложение в ряд Тейлора:
k(ω) = k(ω
0
)
|{z}
k
0
+
dk
dω
ω
0
(ω −ω
0
) + ··· = k
0
+
dk
dω
ω
0
(ω −ω
0
) + ··· .
E
P
≈ E
0
ω
0
+
∆ω
2
Z
ω
0
−
∆ω
2
e
−i
ωt−
k
0
+
(
dk
dω
)
ω
0
(ω−ω
0
)
x
dω =
E
0
ω
0
+
∆ω
2
Z
ω
0
−
∆ω
2
e
−i
ωt−k
0
x−
(
dk
dω
)
ω
0
(ω−ω
0
)x+ω
0
t−ω
0
t
dω =
E
0
ω
0
+
∆ω
2
Z
ω
0
−
∆ω
2
e
−i(ω
0
t−k
0
x)
e
−i
(ω−ω
0
)
t−
(
dk
dω
)
ω
0
x
dω =
-
ξω−ω
0
⇒dξ=dω, ξ∈
[
−
∆ω
2
,
∆ω
2
]
at−
(
dk
dω
)
ω
0
x
E
0
e
−i(ω
0
t−k
0
x)
| {z }
бегущая
бихрома-
тическая
волна с
частотой ω
0
∆ω
2
Z
−
∆ω
2
e
−iξa
dξ = E
0
e
−i(ω
0
t−k
0
x)
·
−
1
ia
e
−iξa
∆ω
2
−
∆ω
2
=
E
0
e
−i(ω
0
t−k
0
x)
·
i
a
·
e
−ia
∆ω
2
− e
ia
∆ω
2
= E
0
e
−i(ω
0
t−k
0
x)
·
i
a
·
−2i sin
a
∆ω
2
=
2E
0
sin
a
∆ω
2
a
· e
−i(ω
0
t−k
0
x)
= 2E
0
sin
аргумент
бегущей волны
z }| {
t −
dk
dω
ω
0
x
!
∆ω
2
!
t −
dk
dω
ω
0
x
| {z }
волна, задающая амплитуду
для огибающей
·e
−i(ω
0
t−k
0
x)
| {z }
бегущая
волна
.
t −
dk
dω
ω
0
x = −
dk
dω
ω
0
x −
dω
dk
k
0
t
!
.
ψ = t −
dk
dω
ω
0
x.
^
sin
ψ
∆ω
2
ψ
.
^ ψ = 0 ⇒ x =
dω
dk
k
0
t.
Максимум не имеет постоянного положения в пространстве, а сам перемещается со
скоростью v
Gr
=
dω
dk
k
0
(см. рис. II.7).
Браницкий А.А. 45 M∀TM∃X 2012

II.1.9 Передача сигналов
Плоская монохроматическая волна
~
E = Re
n
~
F
0
· e
−iω
(
t−
~r·~n
c
)
o
неограниченно простира-
ется во все стороны в пространстве и во времени, не имея, так сказать, ни начала, ни
конца. Кроме того, ее свойства везде и всегда одинаковы: постоянна ее частота, ампли-
туда и расстояние между двумя бегущими гребнями, т. е. длина волны λ. Во всем этом
легко убедиться, рассматривая синусоиду или винтовую линию [1, стр. 217].
Поставим теперь задачу о возможности передачи электромагнитного сигнала на рас-
стояние. Для того чтобы передать сигнал, надо сосредоточить в известном объеме элек-
тромагнитное возмущение. Распространяясь, это возмущение может достичь другой об-
ласти пространства; зарегистрированное каким-либо способом, например радиоприемни-
ком, оно передаст в точку приема сигнал о событии, происшедшем в точке отправления.
(Наше зрительное восприятие также является непрерывной регистрацией электромагнит-
ных (световых) возмущений, исходящих от окружающих объектов). Сигнал должен иметь
определенные границы во времени, чтобы извещать о наступлении и окончании каких-либо
событий [1, стр. 217].
Чтобы передать сигнал, надо как-либо изменить амплитуду волны на некоторое вре-
мя. Например, надо увеличить амплитуду одной из волн синусоиды и ждать, пока это
увеличение амплитуды проявится в принимающем устройстве. Волна, описанная в разде-
ле
II.1.8 Немонохроматическая (несущая) волна
, подходит для передачи данных.
Строго монохроматическая волна, т. е. синусоида, имеет одинаковую амплитуду всегда и
поэтому не годится для передачи сигналов [1, стр. 217].
Таким же образом идеальная плоская волна со строго заданным волновым вектором
не может передавать изображения объектов, ограниченных в пространстве [1, стр. 217].
Как было указано в конце раздела
II.1.8 Немонохроматическая (несущая) вол-
на
, перемещением максимума можно передавать сигналы из одних точек пространства
в другие, потому что этот максимум выделен среди других. Такое сконцентрированное в
пространстве возмущение называется волновым пакетом [1, стр. 219].
Волновой пакет может иметь и не такую форму, как на рисунке II.7, где он относится
к выражению E
P
= 2E
0
sin
t−
(
dk
dω
)
ω
0
x
∆ω
2
t−
(
dk
dω
)
ω
0
x
· e
−i(ω
0
t−k
0
x)
. Выбирая иную зависимость E
0
(ω),
чем в формуле E
P
= E
0
ω
0
+
∆ω
2
R
ω
0
−
∆ω
2
e
−i(ωt−kx)
dω, т. е. не постоянную амплитуду в интервале ча-
стоты ∆ω, а более сложную функцию частоты, можно изменить форму E(x). В частности,
легко придать результирующей амплитуде форму прямоугольника, так что передаваемый
сигнал будет напоминать тире азбуки Морзе [1, стр. 219].
Здесь слово
легко
относится к аналитическому определению величины E
0
(ω), при-
водящей к прямоугольному сигналу. Действительно, формула E
P
= E
0
ω
0
+
∆ω
2
R
ω
0
−
∆ω
2
e
−i(ωt−kx)
dω
есть не что иное, как интегральное преобразование Фурье от функции E
0
(ω) с перемен-
ной ω к функции g(χ) ≡ g
t −
dk
dω
ω
0
x
∆ω
2
≡
2 sin
t−
(
dk
dω
)
ω
0
x
∆ω
2
t−
(
dk
dω
)
ω
0
x
с переменной χ. Но
преобразование Фурье обладает свойством взаимности: если придать функции E
0
(ω) вид,
отвечающий g(χ) по формуле E
P
= 2E
0
sin
t−
(
dk
dω
)
ω
0
x
∆ω
2
t−
(
dk
dω
)
ω
0
x
·e
−i(ω
0
t−k
0
x)
, то
на выходе
по-
лучится сигнал прямоугольной формы E
0
(x) [1, стр. 219].
Имея достаточно большую несущую частоту ω
0
, можно передавать отдельные сигналы
Браницкий А.А. 46 M∀TM∃X 2012

со звуковой частотой так, что они налагаются друг на друга. Иначе говоря, без заметных
искажений удается воспроизвести музыку или речь [1, стр. 219].
Для передачи сигнала всегда необходим некоторый диапазон частот. Монохроматиче-
ская волна со строго определенной частотой однородна по времени: она передает как бы
один сигнал бесконечной длительности. По теореме обращения интегралов Фурье, выра-
жающей их свойство взаимности, заключаем, что сигнал бесконечно малой длительности
требует для своей передачи бесконечно большого диапазона частот. А если длительность
сигнала конечна? Какой диапазон частот требуется для его передачи [1, стр. 219]?
Об этом можно заключить, рассматривая рисунок II.7, изображающий зависимость g
от χ (график, выделенный синим цветом). Для передачи сигнала важна только область
кривой вблизи главного максимума при χ = 0. В единицах χ она по порядку величи-
ны равна π. Следовательно, длительность сигнала определится из такого равенства [1,
стр. 219]:
∆χ =
∆ω
2
· ∆t ∼ π.
Иначе говоря, чтобы передать сигнал длительности ∆t, требуется интервал частот ∆ω,
связанный с ∆t соотношением [1, стр. 220]:
∆ω∆t ∼ 2π.
Если радиостанция должна передавать звуки, воспринимаемые человеческим ухом, то
величина ∆t не больше, чем 0.5 · 10
−4
сек, потому что предельно доступное слуху число
колебаний в секунду составляет 2 · 10
4
. Фактически достаточно передавать частоты не
выше 0.5 · 10
4
. Отсюда ∆ω ∼ 2 · 10
4
, или 0.5 · 10
4
[1, стр. 220].
Диапазон частот ∆ω всегда меньше
несущей
частоты ω
0
, которая даже у самых
длинноволновых передающих станций не меньше, чем 10
6
. Частоту ω
0
надо сравнивать с
интервалом ∆ω порядка 0.5 · 10
4
, потому что срезание самых высоких частот в музыке,
пении и речи не вносит существенных искажений [1, стр. 220].
Возьмем χ при постоянном значении времени t = const. Выбирая снова ∆χ ∼ π, полу-
чим [1, стр. 221].:
∆χ =
∆ω
2
dk
dω
∆x =
∆k∆x
2
∼ π,
или
∆k ·∆x ∼ 2π.
II.2 Излучение электромагнитных волн. Задача об ос-
цилляторе Герца
II.2.1 Излучение электромагнитных волн
∆S −
1
v
2
∂
2
S
∂t
2
= −4πχ(~r, t),
S = (A
x
, . . . , ϕ).
Здесь мы перешли на уровень потенциалов (нужно проверять калибровку).
div
~
A = −
εµ
c
∂ϕ
∂t
.
Браницкий А.А. 47 M∀TM∃X 2012

Будем считать, что в области Ω есть источники волн, во всех остальных точках их нет.
χ =
"
χ, ~r ∈ Ω
0, ~r 6∈ Ω.
A ~r 6∈ Ω ⇒ ∆S −
1
v
2
∂
2
S
∂t
2
= 0.
&%
'$
r
Ω
~
R
Рис. II.8: Сфера
Будем считать, что возможно сферически симмет-
ричное решение, т. е. S = S(R) (см. рис. II.8).
Ω — сфера.
По уравнению IV.5 оператор Лапласа в сферических
координатах выглядит следующим образом:
∆S =
∂
2
S
∂R
2
+
2
R
∂S
∂R
.
∂
2
S
∂R
2
+
2
R
∂S
∂R
−
1
v
2
∂
2
S
∂t
2
= 0
× R.
R
∂
2
S
∂R
2
+ 2
∂S
∂R
=
∂
2
(RS)
∂R
2
.
∂
2
(RS)
∂R
2
−
1
v
2
∂
2
(RS)
∂t
2
= 0.
R · S = f
t −
R
v
= f
0
(R − vt), f — функция второй степени гладкости.
S =
f
t −
R
v
R
.
Вне области Ω решение представляет собой бегущую сферическую затухающую волну.
Математически решение со знаком
”
+“ (второе решение) означает волну, движущуюся
в обратном направлении из бесконечности в Ω (с точки зрения физики это решение имеет
право на существование, но с большими оговорками).
^ ∆S −
1
v
2
∂
2
S
∂t
2
= −4πχ(~r, t).
Догадаемся о виде решения, затем проверим.
Для точечных зарядов: ∆ϕ = 0 ⇒ ϕ =
e
R
.
Для распределенных зарядов: ∆ϕ = −4πρ
e
⇒ ϕ =
R
V
ρ
e
(r)dR
R
.
Проверим: S =
R
V
χ
(
~r,t−
R
v
)
R
dV.
У интеграла при R = 0 есть особенность. Вырезаем V
0
, и тем самым S распадается на
2 интеграла.
S =
Z
V
внутр.
χ
~r, t −
R
v
R
dV
| {z }
S
1
+
Z
V
0
χ
~r, t −
R
v
R
dV
| {z }
S
2
= S
1
+ S
2
.
Браницкий А.А. 48 M∀TM∃X 2012

1.
∆S
1
−
1
v
2
∂
2
S
1
∂t
2
=
Z
V
внутр.
∆
χ
R
−
1
v
2
∂
2
∂t
2
χ
R
dV = 0.
Дифференцирование происходит по точкам конца, интегрирование — по координатам
вектора начала.
За χ скрывается либо ρ
e
, либо j, а они предполагаются второй степени гладкости.
2.
∂
2
S
∂t
2
=
Z
V
0
∂
2
∂t
2
χ
t −
R
v
R
!
dV =
Z
V
0
1
R
∂
2
χ
∂t
2
|{z}
конечная
функция
dV −−−→
R→0
Z
V
0
c
R
dV = c · 4π
Z
R
0
R
2
dR
R
=
4πc
Z
R
0
RdR −−−→
R
0
→0
0.
∆S
2
= div(gradS
2
| {z }
~a
).
div~a = lim
∆V →0
ZZ
S
~ad~s
∆V
.
~a = gradS
2
= grad
Z
V
0
χ
t −
R
v
R
dV =
Z
V
0
grad
χ
R
dV =
Z
V
0
1
R
gradχ
| {z }
↓V
0
→0
0
+χgrad
1
R
!
dV −−−→
V
0
→0
−
Z
V
0
χ
1
R
2
~
R
R
dV.
ZZ
S
~ad~s =
ZZ
S
gradS
2
d~s = −
ZZ
S
Z
V
0
χ
~
R
R
3
dV d~s =
−
Z
V
0
ZZ
S
χ
~r, t −
R
v
|{z}
↓R→0
t
~
R
R
3
d~s
dV −−−→
V
0
→0
−
Z
V
0
χ (~r, t)
ZZ
S
~
R
R
3
d~s
dV.
ZZ
S
~
Ed~s = 4πQ
d
~
E =
ρ
e
~
R
R
3
dV ⇒
~
E =
Z
V
0
ρ
e
~
R
R
3
dV
⇒
ZZ
S
Z
V
0
ρ
e
~
R
R
3
dV
d~s =
Z
V
0
ρ
e
ZZ
S
~
R
R
3
d~s
dV = 4πQ
ZZ
S
~
R
R
3
dV =
"
0, R 6∈ V
4π, R ∈ V
Браницкий А.А. 49 M∀TM∃X 2012

−
Z
V
0
χ (~r, t)
ZZ
S
~
R
R
3
d~s
dV = −4π
Z
V
0
χ(~r, t)dV.
∆S
2
= lim
∆V →0
−4π
R
∆V
χdV
∆V
= −4πχ(~r, t).
Тем самым ∆S −
1
v
2
∂
2
S
∂t
2
= −4πχ(~r, t) выполняется для построенного решения.
ϕ =
1
ε
Z
V
ρ
e
~r, t −
R
v
R
dV.
~
A =
µ
c
Z
V
j
~r, t −
R
v
R
dV.
II.2.2 Задача об осцилляторе Герца
g
g
+
−
l
~
R
~p
Рис. II.9: Модель Герца
Модель Герца — 2 шарика, соединенных проволокой
и противоположно заряженных (см. рис. II.9).
Аналог — конденсатор. Ток движется с
”
+“ на
”
-“,
образуется убывающее магнитное поле (закон Фара-
дея). Конденсатор перезаряжается, и ток движется в
другую сторону (порождается гармонический неста-
ционарный ток). Процесс затухающий, т. к. есть со-
противление (т. е. проводник не модельный).
Вектор электрического момента: ~p = ~p
0
· f(t,
~
R) =
~p
0
· cos
ω
t −
R
c
.
~p
0
= e
~
l.
Вектор Герца:
~
P
~p
R
.
ϕ = −div
~
P .
~
A =
1
c
∂
~
P
∂t
.
~
H = rot
~
A =
1
c
∂rot
~
P
∂t
.
~
E = −gradϕ −
1
c
∂
~
A
∂t
= grad(div
~
P ) −
1
c
2
∂
2
~
P
∂t
2
= rot(rot
~
P ) + ∆
~
P −
1
c
2
∂
2
~
P
∂t
2
| {z }
0
(т. к.
~p
R
является
решением
сферического
волнового
уравнения)
.
~
H =
1
c
∂rot
~
P
∂t
.
~
E = rot(rot
~
P ).
Браницкий А.А. 50 M∀TM∃X 2012
