Волков А.А. Курс физики
Подождите немного. Документ загружается.


Поверхностная плотность связанных зарядов: σ
e,связ.
−(P
n2
− P
n1
).
ρ
e,связ.
и σ
e,связ.
появляются, когда есть скачок.
Потенциал ϕ электростатического поля при наличии в нем диэлектриков равен, оче-
видно, сумме потенциала ϕ
своб.
, возбуждаемого свободными зарядами, и потенциала ϕ
связ.
,
возбуждаемого связанными электрическими зарядами в диэлектриках [3, стр. 81]:
ϕ = ϕ
своб.
+ ϕ
связ.
.
Потенциал свободных зарядов определяется формулой [3, стр. 81]:
ϕ
своб.
=
Z
V
ρ
e,своб.
R
dV +
I
S
σ
e,своб.
R
ds.
В итоге потенциал электростатического поля равен:
ϕ =
Z
V
(ρ
e,своб.
+ ρ
e,связ.
)
R
dV +
I
S
(σ
e,своб.
+ σ
e,связ.
)
R
ds.
Для идеального вещества: ∆ϕ = −4πρ
e
.
Для неидеального вещества среднее значение истинной плотности электричества равно
сумме плотностей электричества свободного и связанного: ρ
e
= ρ
e,своб.
+ ρ
e,связ.
.
∆ϕ = div (gradϕ)
| {z }
−
~
E
= −div
~
E.
−div
~
E = −4π(ρ
e,своб.
+ ρ
e,связ.
).
div
~
E = −4πdiv
~
P + 4πρ
e,своб.
.
div(
~
E + 4π
~
P ) = 4πρ
e,своб.
.
I.5.6 Вектор электрической индукции
Вектор электрической индукции:
~
D
~
E + 4π
~
P .
div
~
D = 4πρ
e,своб.
.
I.5.7 Основные уравнения электростатики в среде
Будем рассматривать только те диэлектрики, для которых существует следующая за-
висимость:
~
P = α
~
E, где α — коэффициент поляризации.
~
D =
~
E + 4π
~
P =
~
E + 4πα
~
E = (1 + 4πα)
| {z }
ε
~
E = ε
~
E, где ε —
коэффициент
диэлектрической проницаемости
.
div
~
D
|{z}
4πρ
e
= div(ε
~
E) =
~
E gradε
|{z}
0
+εdiv
~
E = −εdiv(gradϕ) = −ε∆ϕ.
∆ϕ = −
4π
ε
ρ
e
.
~
E = −gradϕ.
(
rot
~
E = 0
div
~
D = 4πρ
e,своб.
.
Браницкий А.А. 21 M∀TM∃X 2012
I.6 Краевые условия в электростатике. Стандартные по-
становки электростатических задач
I.6.1 Стандартные постановки электростатических задач в про-
водниках
~
E =
ZZ
S
σ
e
~
R
R
3
dR.
Внутри проводника ρ
e
= 0.
Лемма 1.
ZZZ
V
((gradϕ)
2
+ ϕ∆ϕ)dV =
ZZ
S
ϕ
∂ϕ
∂~n
ds.
Доказательство.
ZZZ
V
div~adV =
ZZ
S
~ad~s.
Возьмем в качестве векторного поля ~a = ϕgradϕ.
ZZZ
V
div(ϕgradϕ)dV =
ZZZ
V
(gradϕ · gradϕ
| {z }
grad
2
ϕ
+ϕ div(gradϕ)
| {z }
∆ϕ
)dV.
ZZ
S
ϕgradϕd~s =
ZZ
S
ϕ (gradϕ ·~n)
| {z }
Проекция
gradϕ
на нормаль
ds =
ZZ
S
ϕ
∂ϕ
∂~n
ds.
ZZZ
V
(grad
2
ϕ + ϕ∆ϕ)dV =
ZZ
S
ϕ
∂ϕ
∂~n
ds.
^ ∆ϕ = 0.
Граничные условия:
1. ϕ|
S
= ϕ
0
(задано значение скалярного потенциала на поверхности проводника).
2. e (задан суммарный заряд, скопленный на поверхности проводника).
Докажем единственность решения первой задачи.
Докажем это от противного.
Пусть существуют два решения ϕ
0
и ϕ
00
такие, что ∆ϕ
0
= ∆ϕ
00
= 0, ϕ
0
|
S
= ϕ
00
|
S
= ϕ
0
.
Обозначим: ϕ
000
= ϕ
0
− ϕ
00
.
∆ϕ
000
= ∆(ϕ
0
− ϕ
00
) = ∆ϕ
0
− ∆ϕ
00
= 0;
ϕ
000
|
S
= (ϕ
0
− ϕ
00
)|
S
= ϕ
0
|
S
− ϕ
00
|
S
= 0.
Браницкий А.А. 22 M∀TM∃X 2012

По лемме 1:
ZZZ
V
((gradϕ
000
)
2
+ ϕ
000
∆ϕ
000
|{z}
0
)dV =
ZZ
S
ϕ
000
|{z}
0
∂ϕ
000
∂~n
ds ⇒
ZZZ
V
(gradϕ
000
)
2
dV = 0 ⇒ gradϕ
000
= 0.
ϕ
000
= const ⇒ ϕ
000
= 0, т. к. ϕ
000
|
S
= 0.
ϕ
0
= ϕ
00
.
Докажем единственность решения второй задачи.
Докажем это от противного.
Пусть существуют два решения ϕ
0
и ϕ
00
такие, что ∆ϕ
0
= ∆ϕ
00
= 0, e
0
= e
00
= e.
Обозначим: ϕ
000
= ϕ
0
− ϕ
00
.
∆ϕ
000
= ∆(ϕ
0
− ϕ
00
) = ∆ϕ
0
− ∆ϕ
00
= 0;
e
000
= e
0
− e
00
= 0.
По лемме 1:
ZZZ
V
((gradϕ
000
)
2
+ ϕ
000
∆ϕ
000
|{z}
0
)dV =
ZZ
S
ϕ
000
∂ϕ
000
∂~n
ds ⇒
ZZZ
V
(gradϕ
000
)
2
dV = ϕ
000
ZZ
S
∂ϕ
000
∂~n
ds.
~
E = −gradϕ ⇒
~
E = −
∂ϕ
∂~n
·~n ⇒ E
n
= −
∂ϕ
∂~n
.
E
n2
− E
n1
= 4πσ
000
e
.
Когда речь идет об электростатическом проводнике, то поле внутри проводника равно
нулю (E
n1
= 0).
σ
000
e
= σ
0
e
− σ
00
e
ϕ
000
ZZ
S
∂ϕ
000
∂~n
ds = ϕ
000
ZZ
S
(−4πσ
000
e
)ds = −4πϕ
000
ZZ
S
σ
000
e
ds = −4πϕe
000
= 0.
ZZZ
V
(gradϕ
000
)
2
dV = 0 ⇒ gradϕ
000
= 0 ⇒ ϕ
000
= const.
В этом случае ϕ
000
не обязательно равен нулю. Но поскольку потенциал определяется
с точностью до аддитивной постоянной, то эту константу можно положить равной нулю.
К тому же в большинстве решаемых задач нас интересует не само значение потенциала,
а разность потенциалов.
ϕ
000
= 0.
I.6.2 Метод электрических изображений
В математической физике существует много методов расчета статистических электри-
ческих полей проводников [2, стр. 285].
Рассмотрим некоторые задачи, относящиеся к полям в трех измерениях [2, стр. 285].
Пусть против бесконечной заземленной плоскости, на расстоянии a от нее, помещен
заряд e (см. рис. I.8). Требуется найти электрическое поле [2, стр. 285].
Для решения этой задачи можно применить следующий прием. В точку, находящую-
ся против заряда, на расстоянии a позади проводника, поместим фиктивный заряд — e
Браницкий А.А. 23 M∀TM∃X 2012
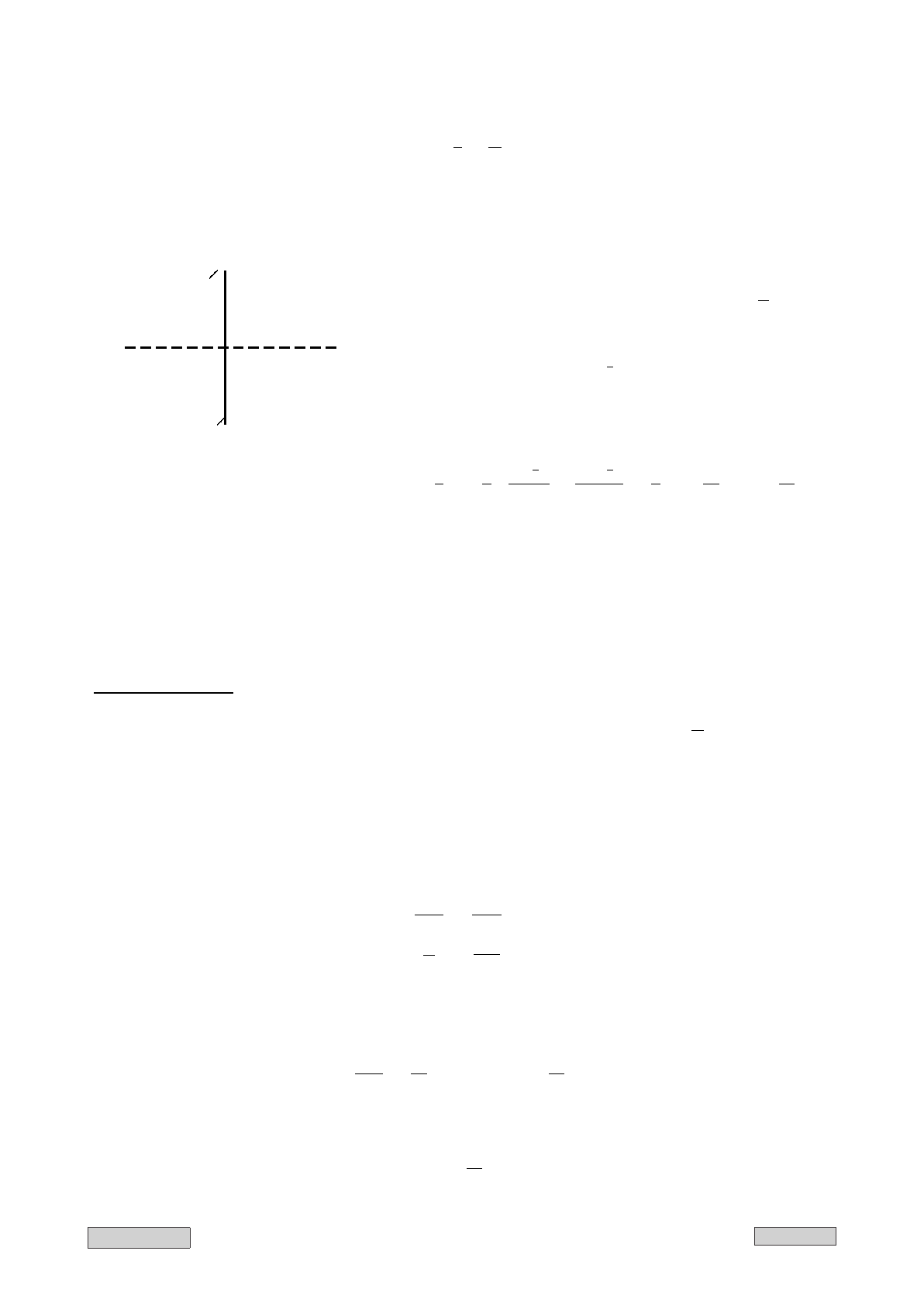
(
изображение заряда e в плоскости
). Тогда потенциал в полупространстве, в котором
находится истинный заряд, равен [2, стр. 285]:
ϕ =
e
r
−
e
r
0
,
где r — расстояние от данной точки до истинного заряда, а r
0
— расстояние до его изоб-
ражения [2, стр. 285].
s
−e
s
e
r
0
r
Рис. I.8: Метод электрических изоб-
ражений: заземленная плоскость
В силу симметрии расположения обоих зарядов по-
тенциал на проводнике равен нулю, т. е. проводник
действительно эквипотенциален. Функция
e
r
0
удовле-
творяет уравнению Лапласа везде в полупростран-
стве перед проводником: в этой области у нее нет
особых точек. Функция
e
r
тоже удовлетворяет урав-
нению Лапласа везде, кроме той точки, где нахо-
дится истинный заряд. Действительно по равенству
IV.5:
∆
e
r
=
2
r
·
∂
e
r
∂r
+
∂
2
e
r
∂r
2
=
2
r
·
−
e
r
2
+ 2 ·
e
r
3
= 0.
Таким образом построено решение уравнения Лапласа и выполнено граничное условие
на плоскости [2, стр. 285].
J
J
E
E
&%
'$
O
Ae
r
B
Рис. I.9: Метод электрических изоб-
ражений: заземленная проводящая
сфера
Эта задача является частной по отношению к бо-
лее общему случаю точечного заряда e около зазем-
ленной проводящей сферы (см. рис. I.9). Здесь надо
сделать следующее построение. Пусть расстояние от
заряда до центра сферы равно R, радиус сферы r
0
.
Отложим от центра отрезок OA =
r
2
0
R
. Проведем про-
извольный радиус OB и соединим точку B прямыми
с точками A и e. Треугольники eOB и AOB подоб-
ны, потому что они имеют общую вершину с оди-
наковым углом при ней O, а стороны, прилегающие
к этому углу, пропорциональны по построению [2,
стр. 285]:
eO
OB
|{z}
R
r
0
=
OB
AO
|{z}
r
0
r
2
0
/R
.
Следовательно пропорциональны им и третьи стороны [2, стр. 286]:
Be
BA
=
R
r
0
⇒ BA = Be ·
r
0
R
.
Поместим теперь в точку A фиктивный заряд e
0
, равный [2, стр. 286]:
e
0
= −
r
0
R
· e.
Браницкий А.А. 24 M∀TM∃X 2012

Тогда потенциал в произвольной точке вне шара равен [2, стр. 286]:
ϕ =
e
r
+
e
0
r
0
,
где r и r
0
— расстояния от этой точки до заряда и до A, соответственно.
На поверхности шара ϕ = 0. Чтобы убедиться в этом, достаточно подставить выра-
жение для e
0
в последнее равенство и положить r
0
= BA. Тогда искомое условие будет
выполнено благодаря доказанной пропорциональности сторон треугольников [2, стр. 286]:
ϕ =
e
r
+
e
0
r
0
=
e
Be
+
e
0
BA
=
e
Be
−
r
0
· e
R · BA
=
e
Be
−
r
0
· e
R · Be ·
r
0
R
= 0.
Если на сфере имеется собственный заряд e
1
, то к потенциалу ϕ достаточно прибавить
слагаемое
e
1
R
. Условие постоянства потенциала на шаре этим не нарушается [2, стр. 286].
I.7 Уравнения магнитостатики в вакууме. Понятие о
векторном потенциале. Векторный потенциал маг-
нитного поля, создаваемого токами, распределенны-
ми по объему. Магнитный момент токов
I.7.1 Уравнения магнитостатики для идеального вещества
rot
~
H =
4π
c
~
j
div
~
H = 0.
Здесь
~
j — объемная плотность тока.
I.7.2 Вектор-потенциал
~
A — векторный потенциал:
~
H rot
~
A.
I.7.3 Вектор-потенциал магнитного поля, создаваемого токами,
распределенными по объему
div(rot~a) ≡ 0 ∀~a ⇒ div(rot
~
A) = 0.
rot(gradψ) ≡ 0 ∀ψ ⇒
~
A
0
=
~
A + gradψ.
Имеем право накладывать дополнительные соотношения:
div
~
A = f (~r) — условие калибровки в общем виде.
В стационарном случае:
div
~
A = 0.
rot
~
H = rot(rot
~
A) =
4π
c
~
j
rot(rot~a) = grad(div~a) − ∆~a ∀~a
⇒ grad(div
~
A
|{z}
0
) − ∆
~
A =
4π
c
~
j.
Браницкий А.А. 25 M∀TM∃X 2012

В магнитостатике:
∆
~
A = −
4π
c
~
j
~
H = rot
~
A.
В электростатике:
(
∆ϕ = −4πρ
e
~
E = −gradϕ.
В электростатике получали:
ϕ =
ZZZ
V
ρ
e
R
dV.
В магнитостатике по аналогии получаем:
~
A =
1
c
ZZZ
V
~
j
R
dV.
Нужно проверить, что div
~
A = 0.
div
~
A = div
a
~
A =
1
c
ZZZ
V
div
a
~
j
R
!
dV.
Дифференцируем по точке конца a, интегрируем по точке начала g.
~
R =
x − x
0
y −y
0
z − z
0
.
R =
p
(x − x
0
)
2
+ (y − y
0
)
2
+ (z −z
0
)
2
.
div
a
~
j
R
!
=
1
R
· div
a
~
j +
~
j · grad
a
1
R
.
Поскольку
~
j зависит от точки начала g, а R зависит от точки конца a, то:
div
a
~
j
R
!
=
~
j · grad
a
1
R
.
grad
a
R = −grad
g
R.
div
a
~
j
R
!
=
~
j · grad
a
1
R
= −
~
j · grad
g
1
R
= −div
g
~
j
R
!
+
1
R
· div
~
j
|{z}
0
(поле
электро-
стати
ческое;
токи
стацио-
нарные)
.
div
a
~
j
R
!
= −div
g
~
j
R
!
.
div
~
A =
1
c
ZZZ
V
div
a
~
j
R
!
dV = −
1
c
ZZZ
V
div
g
~
j
R
!
dV = −
1
c
ZZ
S
0
z}|{
~
j · d~s
R
= 0.
div
~
A = 0.
Браницкий А.А. 26 M∀TM∃X 2012
I.7.4 Вектор-потенциал на больших расстояниях
r
P
r
0
~
R
0
X
Xz
~
j
@
@
@
@I
~
R
*
~
R
0
Рис. I.10: Векторный потенциал на
больших расстояниях
Рассмотрим стационарные замкнутые токи.
(·)P — точка наблюдения, в которой будем измерять
вектор-потенциал
~
A (см. рис. I.10).
Условие удаленности:
R
R
0
1.
~
R
0
=
~
R
0
−
~
R.
R
0
=
q
R
2
0
− 2
~
R
0
~
R + R
2
= R
0
s
1 −
2
~
R
0
~
R
R
2
0
+
R
R
0
2
.
1
R
0
=
1
R
0
1 −
2
~
R
0
~
R
R
2
0
+
R
R
0
2
!
−1/2
| {z }
1−
2R cos(
~
R
0
,
~
R)
R
0
+
R
R
0
2
−1/2
| {z }
1+
R cos(
~
R
0
,
~
R)
R
0
+o
(
R
R
0
)
=1+
(
~
R
0
~
R)
R
2
0
+o
(
R
R
0
)
≈
1
R
0
+
(
~
R
0
~
R)
R
3
0
.
~
A =
1
c
ZZZ
V
~
j(
~
R)
R
0
dV ≈
1
c
ZZZ
V
~
j(
~
R)
R
0
dV +
1
c
ZZZ
V
~
j(
~
R) · (
~
R
~
R
0
)
R
3
0
dV.
Поскольку токи циркулируют по замкнутому контуру, то:
1
cR
0
ZZZ
V
~
j(
~
R)dV = 0.
~
A ≈
1
cR
3
0
ZZZ
V
~
j · (
~
R
~
R
0
)dV.
I.7.5 Вектор магнитного момента
[[
~
R,
~
j],
~
R
0
] = −[
~
R
0
, [
~
R,
~
j]] = −
~
R(
~
R
0
~
j) +
~
j(
~
R
0
~
R).
~
j(
~
R
0
~
R) = [[
~
R,
~
j],
~
R
0
] +
~
R(
~
R
0
~
j) =
1
2
[[
~
R,
~
j],
~
R
0
] +
1
2
~
j(
~
R
0
~
R) −
~
R(
~
R
0
~
j)
+
~
R(
~
R
0
~
j).
~
A =
1
2cR
3
0
ZZZ
V
[[
~
R,
~
j],
~
R
0
]dV +
1
2cR
3
0
ZZZ
V
~
j(
~
R
0
~
R) +
~
R(
~
R
0
~
j)
dV
| {z }
~
k
∀~a = const ^ ~a
~
k =
ZZZ
V
(~a
~
j)(
~
R
0
~
R) + (~a
~
R)(
~
R
0
~
j)
dV.
Браницкий А.А. 27 M∀TM∃X 2012

^
~
jgrad
(~a
~
R)(
~
R
0
~
R)
=
~
j
(~a
~
R) grad(
~
R
0
~
R)
|
{z }
~
R
0
+(
~
R
0
~
R) grad(~a
~
R)
| {z }
~a
=
~
j
~
R
0
(~a
~
R) + (
~
R
0
~
R)~a
.
~a
~
k =
ZZZ
V
~
jgrad
(~a
~
R)(
~
R
0
~
R)
dV.
div(ϕ ·
~
j) = gradϕ ·
~
j + ϕ · div
~
j
|{z}
0
(токи
стацио-
нарные)
= gradϕ ·
~
j.
A ~a = const.
A ϕ = (~a
~
R)(
~
R
0
~
R).
div
(~a
~
R)(
~
R
0
~
R) ·
~
j
=
~
j · grad
(~a
~
R)(
~
R
0
~
R)
.
~a
~
k =
ZZZ
V
div
(~a
~
R)(
~
R
0
~
R) ·
~
j
dV =
ZZ
S
(~a
~
R)(
~
R
0
~
R) ·
~
jd~s
|{z}
0
= 0 ⇒
~
k = 0.
~
A =
1
2cR
3
0
ZZZ
V
[[
~
R,
~
j],
~
R
0
]dV.
Вектор магнитного момента: ~µ =
1
2c
RRR
V
[
~
R,
~
j]dV.
~
A =
1
R
3
0
1
2c
ZZZ
V
[
~
R,
~
j]dV,
~
R
0
=
[~µ,
~
R
0
]
R
3
0
.
Если система от стационарных магнитных токов, то магнитный момент не зависит от
выбора центра.
~
R =
~
R
0
0
+ ~a
~a = const
)
⇒ ~µ =
1
2c
ZZZ
V
[
~
R
0
0
,
~
j]dV +
1
2c
ZZZ
V
[~a,
~
j]dV
| {z }
[~a,
RRR
V
~
jdV
|{z}
0
]
=
1
2c
ZZZ
V
[
~
R
0
0
,
~
j]dV.
I.8 Магнитное поле в среде. Векторы напряженности и
индукции магнитного поля в среде
I.8.1 Микро- и макроскопические значения физических величин
До сих пор мы не обращали достаточного внимания на то обстоятельство, что поле
каждой молекулы диэлектрика в непосредственной близости от нее должно чрезвычайно
быстро изменяться от точки к точке (например при переходе от положительных к отрица-
тельным зарядам молекулы). Правда, эти изменения поля протекают в микроскопическом
масштабе и недоступны нашему макроскопическому наблюдению. Измеряя, например, по-
ле в жидком диэлектрике путем погружения в него пробного заряда, например, достаточ-
но малого заряженного металлического шарика, мы, очевидно, измеряем среднее из тех
значений, которые имеет напряженность поля
~
E на поверхности этого шарика [3, стр. 93].
Браницкий А.А. 28 M∀TM∃X 2012

Чтобы уточнить понятие среднего значения, мы введем слеующую терминологию,
предложенную Лоренцем. Мы будем называть физически бесконечно малыми в отличие
от математически бесконечно малых такие элементы объемов, поверхностей и линий,
которые одновременно удовлетворяют следующим двум требованиям [3, стр. 94]:
а) Физически бесконечно малые элементы должны быть чрезвычайно велики по срав-
нению с расстояниями между молекулами среды, а стало быть, и по сравнению с
микроскопическими неоднородностями среды и поля.
б) Вместе с тем физически бесконечно малые элементы должны быть чрезвычайно
малы по сравнению с макроскопическими неоднородностями поля и среды; другими
словами, средние значения физических величин (например ϕ,
~
E, E и т. д.) в любом
из этих элементов должны бесконечно мало отличаться от средних значений этих
величин в смежных с ними элементах
4
.
Даже в газообразных, не говоря уже о жидких и твердых, телах расстояния между мо-
лекулами столь малы по сравнению с макроскопическими неоднородностями изучаемых
обычно полей, что почти всегда оказывается возможным одновременно удовлетворять обо-
им этим условиям. Конечно, возможны и такие случаи, когда приведенные условия вза-
имно исключают друг друга; так, например, длина волны жестких рентгеновских лучей,
могущая служить мерой неоднородности поля этих лучей, меньше расстояния между мо-
лекулами материальных тел [3, стр. 94].
Оставляя в стороне подобные исключительные случаи, мы будем в дальнейшем под
макроскопическими величинами понимать средние значения физических величин в фи-
зически бесконечно малом объеме. Другими словами, под макроскопическим значением
произволной физической (скалярной или векторной) величины ψ (например ϕ,
~
E, ρ
e
) в
данной точке P пространства мы будем понимать среднее из истинных или микроскопи-
ческих значений этой величины в физически бесконечно малом объеме ∆V , окружающем
точку P [3, стр. 94]:
ψ
макро
=
˜
ψ
микро
=
1
∆V
Z
V
ψ
микро
dV.
Среднее значение производной по координате (а также и по времени) от произвольной
величины ψ равно производной от среднего значения этой величины:
˜
∂ψ
∂x
=
∂
˜
ψ
∂x
,
где волнистая черта сверху означает образование среднего [3, стр. 95].
I.8.2 Магнетики, или магнитное поле в среде. Молекулярные токи
и токи проводимости
Магнетик при внесении в магнитное поле порождает или изменяет его.
Устройство магнетика:
– токи проводимости: связаны со свободными зарядами (перемещаются на микроско-
пические расстояния;
– молекулярные токи: связаны со связанными зарядами (локализованы в малых обла-
стях, являются стационарными токами); не обязательно молекулярные токи внутри
одного атома/молекулы.
4
За исключением элементов, отделенных друг от друга поверхностями разрыва, если только мы вообще
захотим ввести в рассмотрение (в сущности, фиктивные) поверхности разрыва.
Браницкий А.А. 29 M∀TM∃X 2012
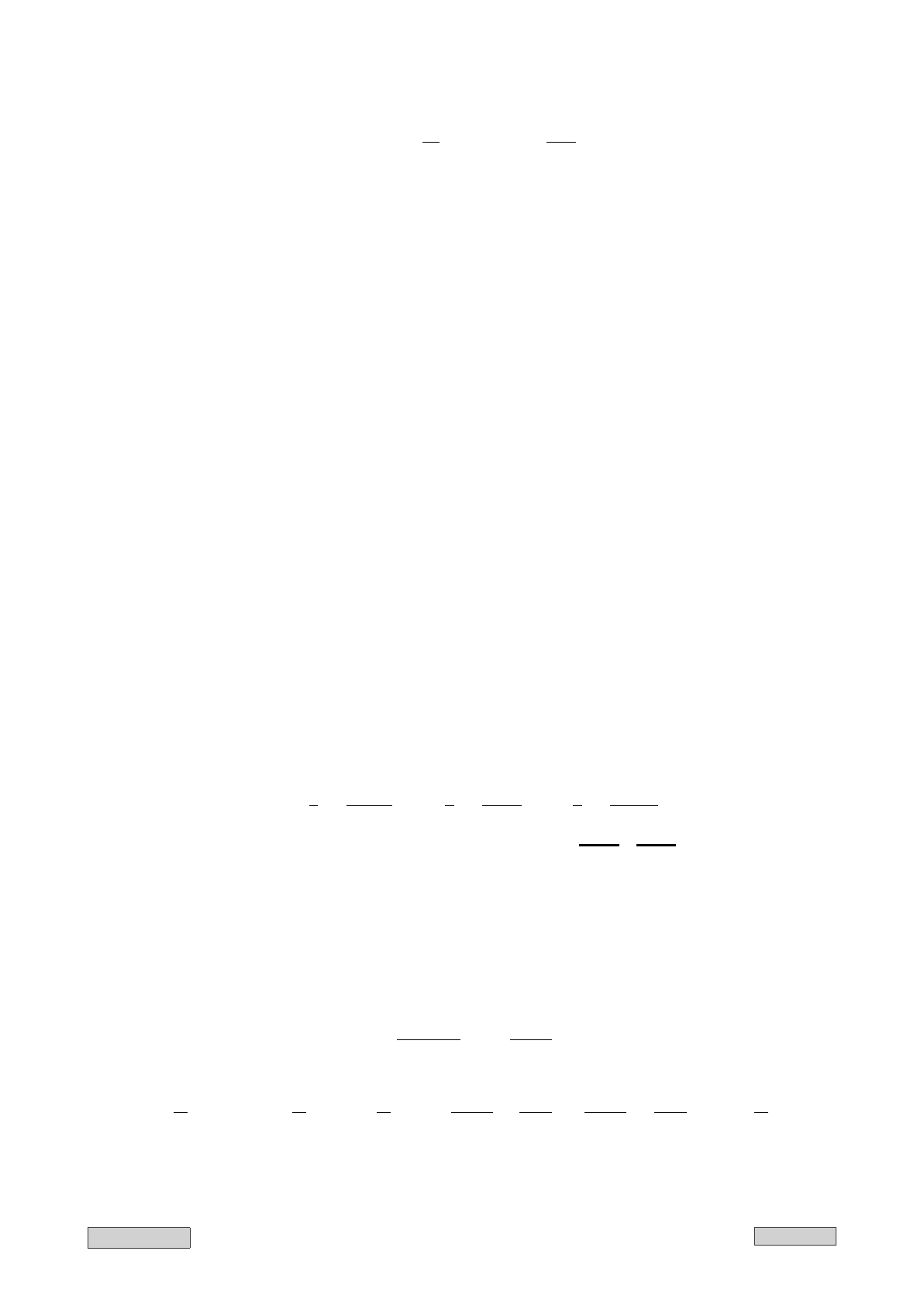
Вектор намагничения (вектор плотности магнитного момента):
~
I lim
∆V →0
1
2c
Z
∆V
[
~
R,
~
j]dV ·
1
∆V
.
~
IdV = d~µ.
Поле намагниченных магнетиков, как и всякое магнитное поле, создается циркулиру-
ющими в магнетике электрическими токами [3, стр. 224].
Рассмотрим сначала магнетик, не проводящий электричества и построенный из ней-
тральных молекул (газы, жидкости) или из закрепленных в определенных положениях
ионов (ионная кристаллическая решетка или аморфный твердый диэлектрик). Хотя сред-
няя плотность тока в такой среде и равна нулю и переноса электрических зарядов на
макроскопические расстояния в ней не происходит, однако внутри отдельных молекул
или ионов имеет место движение электронов, соответствующее определенному распреде-
лению токов. Эти токи называются молекулярными; в ненамагниченных магнетиках они
распределены совершенно хаотично, и магнитные поля их в среднем взаимно компенси-
руются. Намагниченный же магнетик характеризуется упорядоченностью молекулярных
токов, благодаря которой результирующее магнитное поле этих токов отлично от нуля [3,
стр. 224].
В магнетиках, являющихся проводниками (металлы, электролиты и т. п.), нужно, оче-
видно, проводить различие между токами проводимости
~
j
пров.
, соответствующими движе-
нию зарядов, переносящих макроскопический ток (свободные электроны в металлах, ионы
в электролитах и ионизированных газах) и токами молекулярными
~
j
молек.
в нейтральных
молекулах электролитов, в закрепленных ионах, образующих твердый кристаллический
остов металлов и т. п.:
~
j
микро
=
~
j
пров.
+
~
j
молек.
,
где индекс
микро
означает истинную микроскопическую плотность тока в среде в от-
личие от средней макроскопической плотности
~
j [3, стр. 225].
Осуществим процедуру усреднения, перейдя на микроуровень:
˜
~
A
микро
=
1
c
Z
V
˜
~
j
микро
R
dV =
1
c
Z
V
˜
~
j
.
~
j
пров.
R
dV +
1
c
Z
V
˜
~
j
молек.
R
dV
| {z }
˜
~
A
молек.
.
˜
~
j
микро
=
˜
~
j
пров.
+
˜
~
j
молек.
.
~
j
˜
~
j
пров.
,
˜
~
j
молек.
−?.
Рассмотрим модель идеального магнетика (нет свободных зарядов ⇒ нет токов прово-
димости).
˜
~
A
молек.
=
Z
V
[
~
IdV,
~
R]
R
3
=
Z
V
[
~
I,
~
R]
R
3
dV =
~
A
1
.
rot
~
I
R
!
=
grad
1
R
,
~
I
+
1
R
rot
~
I =
[
~
R,
~
I]
R
3
+
rot
~
I
R
⇒
[
~
I,
~
R]
R
3
=
rot
~
I
R
− rot
~
I
R
!
.
Браницкий А.А. 30 M∀TM∃X 2012
