Вольдек А.И. Электрические машины
Подождите немного. Документ загружается.


ции катушек. При короне воздух ионизируется, образуется озон,
который является активным окислительным элементом и вызывает
окисление азота. Ввиду наличия влаги образуются азотистая и
азотная кислоты, которые разрушают изоляцию. Для предотвраще-
ния появления короны поверхность изоляции покрывается слоем
полупроводящего лака, который вызывает перераспределение элек-
трического поля. Этот лак содержит обычно сажу.
Глава двадцать вторая
НАМАГНИЧИВАЮЩИЕ СИЛЫ ОБМОТОК
ПЕРЕМЕННОГО ТОКА
§ 22-1. Намагничивающая сила фазы обмотки
Допущения. Приступая к изучению магнитного поля, создавае-
мого обмоткой переменного тока в воздушном зазоре, допустим
сначала, что 1) магнитная проницаемость стали сердечников р
с
=
оо; 2) пазы и явновыраженные полюсы отсутствуют и воздушный
зазор является равномерным; 3) катушечные стороны расположены
в воздушном зазоре и имеют в сечении вид бесконечно тонкой ленты
с шириной, равной величине зазора 6; 4) величина зазора б мала по
сравнению с радиусом статора и полюсным делением. При этих
условиях линии магнитной индукции в воздушном зазоре прямоли-
нейны и перпендикулярны поверхностям зазора. Рассмотрение
вопроса при подобных допущениях позволяет выявить главные
особенности поля в воздушном зазоре. Влияние этих допущений
может быть учтено дополнительно (см. § 23-1, 23-4).
Рассмотрим прежде всего обмотку с целым числом пазов на по-
люс и фазу.
Н. с. катушек с полным шагом. Пусть на каждом двойном по-
люсном делении 2т расположено по одной катушке с w
K
витками и
шагом у = г. Эти катушки сдвинуты относительно друг друга на
2т, принадлежат одной фазе и нагружены током t'
K
(рис. 22-1, а).
Вид возникающего при этом магнитного поля показан на этом же
рисунке.
Применим к одной йз магнитных линий рис. 22-1, а закон пол-
ного тока:
ф
Н
d\ =Wgi
K
. (22-1)

Так как, согласно принятому допущению, для стали = оо,
то в сердечниках Я
с
= 0 и вместо (22-1) получим
2Я6 = w
K
i
K
, (22-2)
где Я — напряженность магнитного поля в зазоре.
а
) V Г Г
Рис. 22-1. Магнитное поле и н. с. катушек с пол-
ным шагом
На основании выражения (22-2) индукция в зазоре
Назовем величину
Л
в
= ро/б
удельной магнитной проводимостью воз-
душного зазора и величину —
F
Kt
= w
K
ij2 (22-4)
намагничивающей силой (н. с.) или магнито-
движущей с и л о й (м. д. с.) катушки на один зазор. Тогда
В = (22-5)
Указанный ряд катушек создает в зазоре прямоугольную волну
магнитной индукции В (рис. 22-1, ф. В соответствии с выражением
(22-5) эта волна в другом масштабе представляет собой также волну
н. с. данного ряда катушек. Так как, согласно (22-5), величина В

пропорциональна F
Kt
, то в дальнейшем можно рассматривать на-
магничивающие силы.
Прямоугольную волну н. с. F
K
(рис. 22-1, б) можно разложить
в ряд Фурье. Так как отрицательные полупериоды этой волны при
их сдвиге на угол а = п симметричны (относительно оси абсцисс)
положительным полупериодам, то волна содержит только нечетные
гармоники (v = 1, 3, 5...). Выберем начало осей по оси симметрии
катушки. Тогда кривая рис. 22-1, б будет симметрична относительно
оси ординат и содержать только косинусные члены.
Таким образом,
F
K
= F
Ktl
cos а+F
Kt3
cos За +...+Fcos va +... (22-6)
Согласно теории рядов Фурье, амплитуда v-й гармоники
2Я
F
K
,
V
= ^ F
K
cos va da,
о
а для симметричной кривой рис. 22-1, б
я
2
F
Kt
v = — ^
F
*i
cos va da
= ^
F
«t s in ^
•
(22-7)
о
На рис. 22-1, б показаны кривые гармоник н. с. v = 1 и v = 3.
Если ток катушки переменный
i
K
= j/2 I
K
cosat, (22-8)
то на основании выражений (22-4) и (22-7)
F
Ktv
= F
KV
cos at, (22-9)
где
с, 21/2 , ГЯ mc, ,
^«у = -^-ЮЕ/«81П-g-. (22-10)
Равенство (22-6) при этом приобретает вид
F
K
= 2 F
KV
cosat cosva. (22-11)
V=l, 3. s
Согласно равенству (22-11), н. с. рассматриваемого ряда кату-
шек состоит из бесконечного ряда гармоник v, каждая из которых
изменяется в пространстве (cos va) и во времени (cos со/) по синусои-
дальному закону. Иными словами, н. с. этого ряда катушек пред-
ставляет собой ряд неподвижных пространственных гармоник
(рис. 22-1, б), амплитуды которых Fпульсируют во времени по
синусоидальному закону в пределах от +F
KV
до —F
KV
. Каждая
гармоника н. с. создает подобную же гармонику магнитного поля
в соответствии с соотношением (22-5). Прямоугольная волна н. с.
и магнитного поля (рис.
22-1, б) также пульсирует
во времени, и ее ордина-
ты F
Kt
изменяются от зна-
чения +F
Km
до
1
кш»
причем на основании вы-
ражений (22-4) и (22-8)
F
Km
= ¥§-wJ
K
. (22-12)
Н. с. катушечной груп-
пы с полным шагом. На
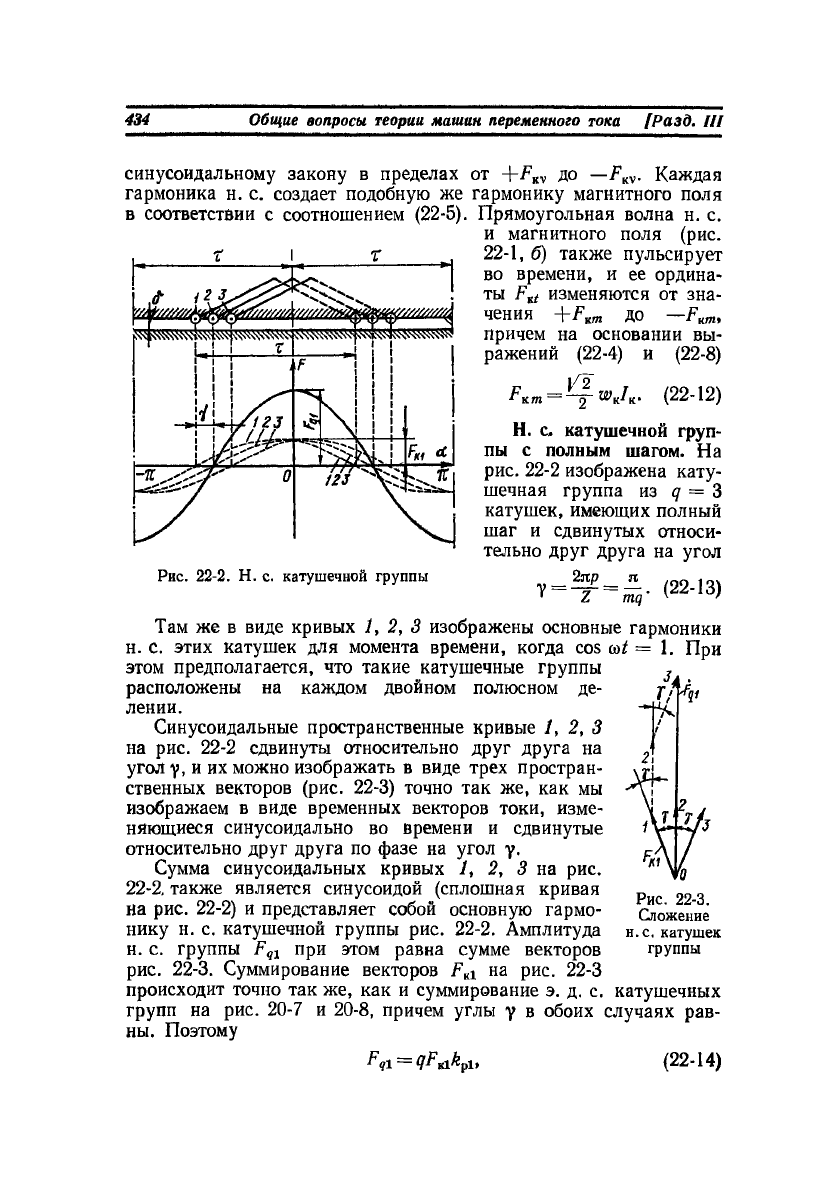
рис. 22-2 изображена кату-
шечная группа из q = 3
катушек, имеющих полный
шаг и сдвинутых относи-
тельно друг друга на угол
v=¥=5- (
22
-»з)
Там же в виде кривых 1, 2, 3 изображены основные гармоники
н. с. этих катушек для момента времени, когда cos at = 1. При
этом предполагается, что такие катушечные группы
расположены на каждом двойном полюсном де-
лении.
Синусоидальные пространственные кривые 1, 2, 3
на рис. 22-2 сдвинуты относительно друг друга на
угол у, и их можно изображать в виде трех простран-
ственных векторов (рис. 22-3) точно так же, как мы
изображаем в виде временных векторов токи, изме-
няющиеся синусоидально во времени и сдвинутые
относительно друг друга по фазе на угол у.
Сумма синусоидальных кривых 1, 2, 3 на рис.
22-2, также является синусоидой (сплошная кривая
на рис. 22-2) и представляет собой основную гармо-
нику н. с. катушечной группы рис. 22-2. Амплитуда
н. с. группы F
q
j при этом равна сумме векторов
рис. 22-3. Суммирование векторов F
Kl
на рис. 22-3
происходит точно так же, как и суммирование э. д. с. катушечных
групп на рис. 20-7 и 20-8, причем углы у в обоих случаях рав-
ны. Поэтому
Рис. 22-3.
Сложение
н.с. катушек
группы
Fqi = qF
Kl
k
pl
, (22-14)
где k
pl
— коэффициент распределения обмотки для v = 1, опре-
деляемый равенствами (20-15) и (20-23). Н. с. v-x гармоник кату-
шек катушечной группы
сдвинуты относительно друг
друга на угол, больший
в v раз, т. е. на vy. Просум-
мировав эти н. с. так же,
как и на рис. 22-2 и 22-3,
получим амплитуду н. с.
v-й гармоники группы:
Fqv
= qF
KV
k
pV
, (22-15)
где коэффициент распреде-
ления fe
pV
определяется ра-
венствами (20-27) и (20-28).
Обратим внимание на то,
что ось н. с. катушечной
группы (рис. 22-2) совпа-
дает с осью симметрии
группы. Поэтому н.с. груп-
пы при выборе начала ко-
ординат по рис. 22-2 вы-
ражается равенством (22-11)
при замене F
KV
на F
9V
.
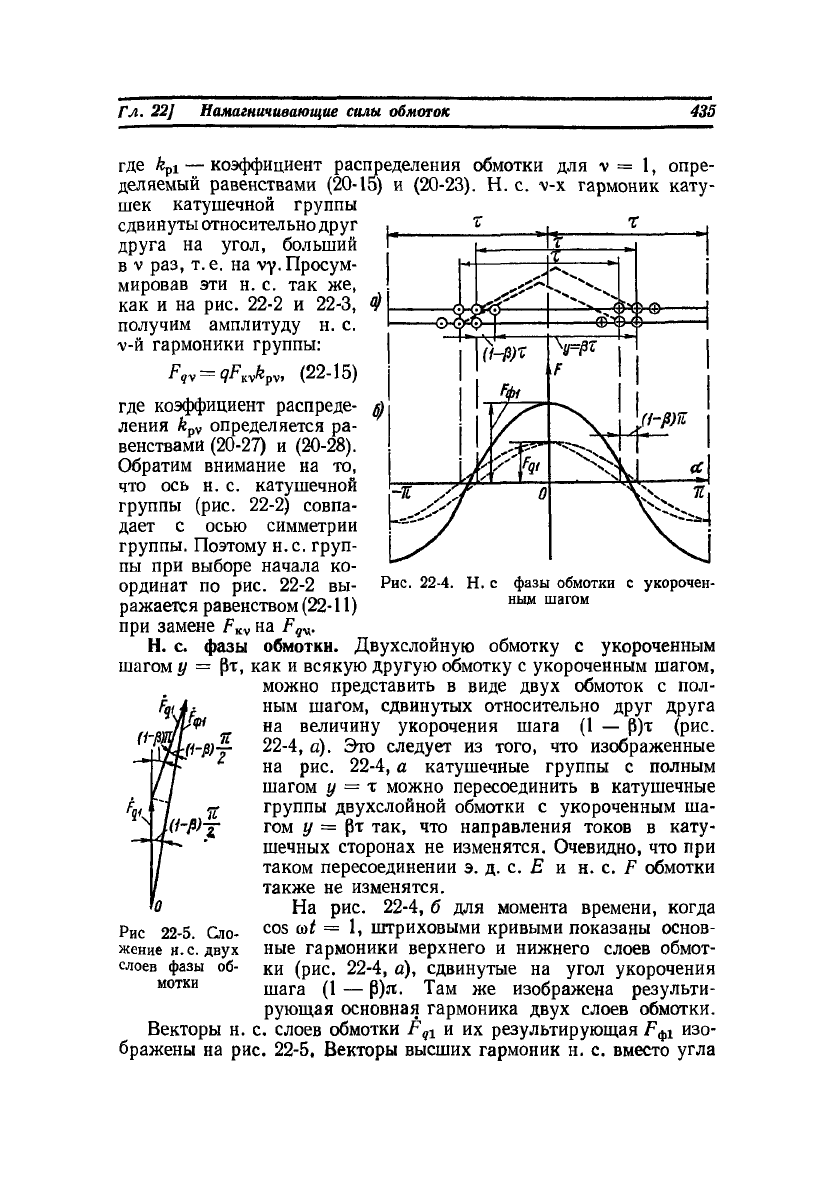
Н. с. фазы обмотки. Двухслойную обмотку с укороченным
шагом у = рт, как и всякую другую обмотку с укороченным шагом,
можно представить в виде двух обмоток с пол-
ным шагом, сдвинутых относительно друг друга
на величину укорочения шага (1 — Р)т (рис.
22-4, а). Это следует из того, что изображенные
на рис. 22-4, а катушечные группы с полным
шагом у = т можно пересоединить в катушечные
группы двухслойной обмотки с укороченным ша-
гом у = рт так, что направления токов в кату-
шечных сторонах не изменятся. Очевидно, что при
таком пересоединении э. д. с. Е и н. с. F обмотки
также не изменятся.
На рис. 22-4, б для момента времени, когда
cos at = 1, штриховыми кривыми показаны основ-
ные гармоники верхнего и нижнего слоев обмот-
ки (рис. 22-4, а), сдвинутые на угол укорочения
шага (1 — Р)я. Там же изображена результи-
рующая основная гармоника двух слоев обмотки.
Векторы н. с. слоев обмотки F
ql
и их результирующая изо-
бражены на рис. 22-5. Векторы высших гармоник н. с. вместо угла
ным шагом
Рис 22-5. Сло-
жение н. с. двух
слоев фазы об-
мотки

(1 — Р)я будут сдвинуты на угол v (1 — Р)я, Поэтому на основании
рис 22-5 для амплитуды v-й гармоники н. с. фазы получим
/> = 2/vcosv(l
я
2 '
Подставим сюда F
gv
из (22-15), а затем F
KV
из (22-10) и учтем, что
0V
ГЯ ,, о\ я \п ( УЯ уВя
sin -д- cos
V
(1
—
Р)-р"
=
sin -х-(cos COS c-
. yn уВп\
2 +sin
T
sin-i-j =
, УЯ vBn УВЯ
= Sin
2
Sin—fc—
= sin
—ь—
так как при нечетном v
\'Я
cos Y=0;
уп , ,
sin-g- = ± 1.
Тогда найдем, что
где величина
— 2qw
K
k
yv
kpvI
к
, __ Уря
"yv —
Sin 2 i
(22-16)
совпадающая с k
yv
по формуле (20-26), представляет собой коэф-
фициент укорочения шага обмотки для v-й гармоники
Число последовательно соединенных витков фазы двухслойной
обмотки
W
•
. 2pqw
K
(22-17)
и ток катушки
/к = На,
(22-18)
где а — число параллельных ветвей обмотки и / — ток фазы.
Введя в равенство (22-16) значения w и /, определяемые форму-
лами (22-17) и (22-18), получим окончательное выражение для
амплитуды v-й гармоники н. с. фазы обмотки:
р __ 21/2 _ Bffe
0
6v j __ Q g Wkобу j
я \p
\p
где
Aq6V — Ap
V
Ay
V
(22-19)
(20-20)
является обмоточным коэффициентом v-й гармоники.

Выражение (22-19) действительно также и для однослойных об-
моток при соответствующим образом вычисленных значениях £
o6v
(см. § 21-3).
Для н. с. фазы в целом действительно выражение
F<bt= 2
*>vCOS a>t
cosva,
V = l.
3, 8
(22-21)
которое получим из соотношения (22-11) при замене F
KV
на
Начало осей при этом совпадает с осью фазы обмотки
(рис. 22-4).
Согласно равенству (22-21), н. с. фазы F& также представляет
собой сумму неподвижных в пространстве и пульсирующих во
времени гармоник.
Как будет установлено в последующих главах, высшие гармо-
ники н. с. вызывают в машинах ряд нежелательных явлений (до-
бавочные вращающие моменты и потери, увеличение индуктивных
сопротивлений обмоток и пр.). Поэтому целесообразно добиваться
их уменьшения.
Из формулы (22-19) следует, что величина обратно пропор-
циональна порядковому номеру гармоники v и зависит от обмоточ-
ного коэффициента £
o6v
.
Поскольку k
yv
и k
pV
в формулах (22-19) и (22-20) вычисляются
по тем же выражениям, что и при определении э. д. с. обмотки,
то отсюда следует, что меры, принимаемые для подавления выс-
ших гармоник э. д. с. (укорочение шага и распределение обмотки),
приводят также к подавлению высших гармоник н. с.
Коэффициент скоса пазов k
z4
[см. выражение (20-29] в формулы
(22-19) и (22-20) не входит, так как н. е., создаваемая обмоткой,
ориентирована вдоль ее пазов, как по направляющим, и поэтому
скос пазов вызывает лишь скос волн н. с. в тангенциальном напра-
влении, но не изменяет их амплитуды.
Для гармоники н. с. зубцового порядка \
г
, определяемых равен-
ством (20-34), коэффициент k
yv
k
pV
= ±k
yl
k
pl
, и поэтому из числа
высших гармоник эти гармоники выражены наиболее сильно. При
q = 2, например, гармониками зубцового порядка будут v = v* =
= 11, 13, 23, 25..., а при q = 3 — соответственно = 17, 19, 35,
37... При <7=1 все высшие гармоники н. с. являются гармониками
зубцового порядка. Очевидно, что ослабления гармоники н. с. зуб-
цового порядка можно достичь только увеличением q, так как при
этом порядок v
2
увеличивается.

438 Общие вопросы теории машин переменного тока [Разд. Ill
Вращающиеся волны н. с. Используя известную тригонометри-
ческую формулу, каждый член равенства (22-21) можно выразить
в следующем виде:
F^vcos cos va =
COS
(at
—
va) + cos(<в< + va).
(22-22)
Каждый из правых членов этого равенства представляет собой
вращающуюся волну н. е., которая распределена в пространстве
вдоль координаты а по синусоидальному закону и имеет амплитуду
V
2
F^y. Действительно, вообразим, что мы наблюдаем за какими-
либо точками этих двух волн, имеющими постоянные значения н, с.
Тогда для этих точек
cos (at
—
va) = const; cos (at+va) = const
и, следовательно,
totf —va = const; wtf+va = const.
Дифференцируя последние равенства no t, найдем
da _
<а
_
da _ со
dt ~ V' dt~~\- KH-ld)
Производные в равенствах (22-23) представляют собой угловые
скорости вращения волн, выражаемые в радианах (электрических)
в секунду. Согласно равенствам (22-23), первый член правой части
(22-22) представляет собой прямую волну ^">oj,T. е. волну,
вращающуюся в направлении положительных углов а, а второй
член — обратную волну < 0j. Угловые скорости вращения гар-
монических волн обратно пропорциональны порядку гармоники v.
Основные гармоники (v = 1) вращаются с электрической угловой
скоростью
fii =
ю
= 2я[,
(22-24)
что соответствует скорости вращения поля согласно выражению
(19-2).
о
Действительно, на основании равенства (19-2) угловая скорость
вращения поля в механических единицах угла
и в электрических единицах угла
S2
1
= pfi
lMX
= 2n;/
1
.
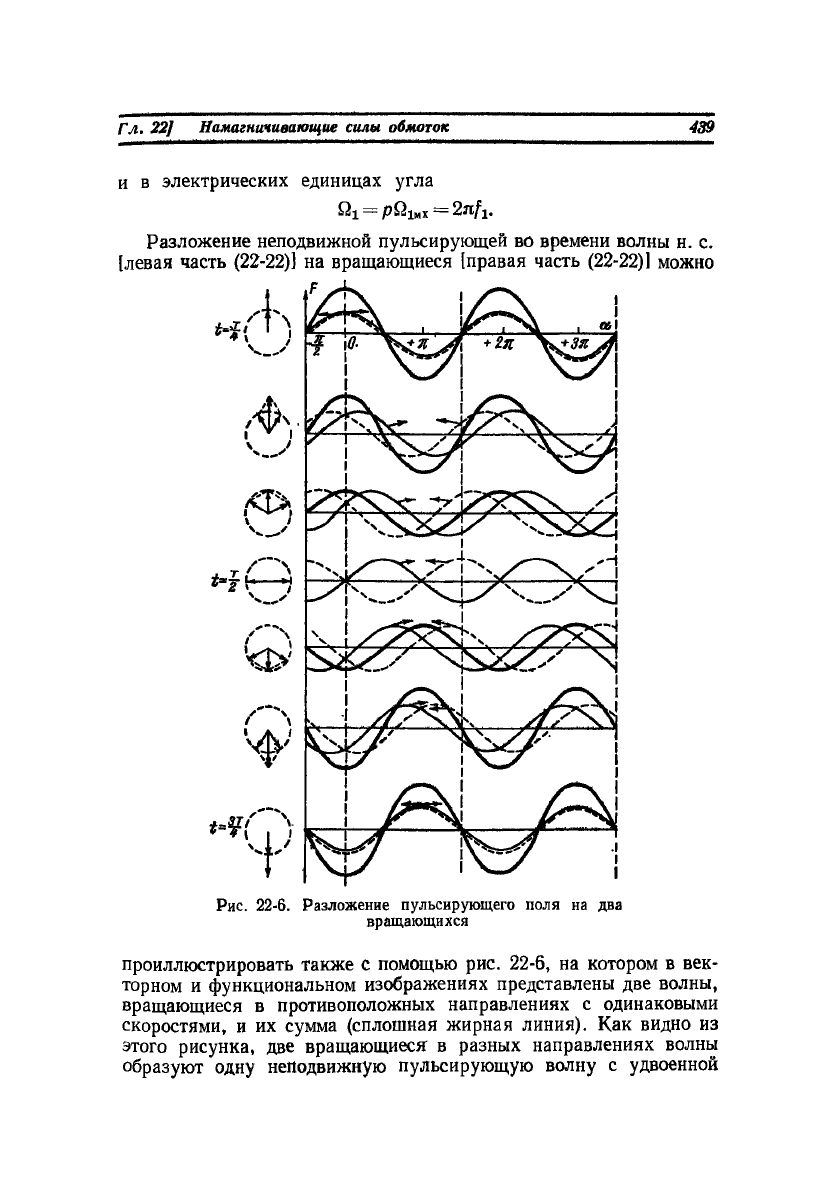
Разложение неподвижной пульсирующей во времени волны н. с.
[левая часть (22-22)] на вращающиеся [правая часть (22-22)1 можно
Рис. 22-6. Разложение пульсирующего поля на два
вращающихся
проиллюстрировать также с помощью рис. 22-6, на котором в век-
торном и функциональном изображениях представлены две волны,
вращающиеся в противоположных направлениях с одинаковыми
скоростями, и их сумма (сплошная жирная линия). Как видно из
этого рисунка, две вращающиеся в разных направлениях волны
образуют одну неподвижную пульсирующую волну с удвоенной

амплитудой и наоборот — одна пульсирующая волна разлагается
на две волны с половинными амплитудами, вращающимися в про-
тивоположных направлениях.
Очевидно, что полученные в данном параграфе результаты це-
ликом применимы для н. с. однофазной обмотки. Эту н. с. в соот-
гетствиии с изложенным можно рассматривать состоящей из непод-
вижных пульсирующих или вращающихся в противоположных
направлениях гармоник н. с.
§ 22-2. Намагничивающие силы многофазных обмоток
Н. с. трехфазной обмотки при симметричной нагрузке. Допустим,
что трехфазная обмотка с целым" числом пазов на полюс и фазу
(рис. 22-7, а) нагружена симметричными токами:
i
a
= j/jT/ cos at;
i
b
= У"2 / cos
i^w/
-
2n\
"3 )•
i
c
- У"2 I cos (at
—
4n\
3 )•
(22-26)
Направим ось а в сторону чередования фаз и отметим оси отдель-
ных фаз обмотки (рис. 22-7, б). Н. с. v-x гармоник отдельных фаз
относительно осей своих фаз выражается равенством (22-22), если
для фаз В и С заменить сot соответственно на сot — 2я/3 и сot — 4я/3.
Для суммирования н. с. отдельных фаз будем отсчитывать углы а
от оси фазы А. Тогда для фаз В и С в выражении (22-22) нужно
заменить угол а соответственно на а — 2я/3 и а — 4я/3. Таким
образом, вращающиеся волны v-x гармоник н. с. отдельных фаз
выражаются равенствами:
F
a
\ = I COS (Шt — va) + У cos (сot + va);
Fb\ =
-
cos [(at - Щ - v (a - ^ jj +
+ "9-^«BV COS И/
Fcv =
"2
F4,
V
cos j^ctf - У
J
-
V
(a - +
+ у
F
4>V cos - Y J + V (A - ^ J J.
(22-27)
