Voit J. The Statistical Mechanics of Financial Markets

Подождите немного. Документ загружается.

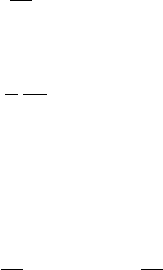
210 7. Derivative Pricing Beyond Black–Scholes

lengthy integrals. Apparently, this theory gives rather realistic option prices.

When represented in terms of an implied volatility (invert the Black–Scholes

equation for the true option price and solve for σ), one nicely reproduces the

main features of the characteristic skewed volatility smile observed in real

option markets [169].

7.7 Path Integrals: Integrating the Fat Tails

into Option Pricing

When deriving the Black–Scholes solution of option pricing and hedging in

Sect. 4.5.1, we mentioned that the Black–Scholes equation could be solved

by path-integral methods, deﬁning a Black–Scholes “Hamiltonian”, (4.93),

on the way [51]. Also, the integral framework based on a global wealth bal-

ance and the minimal variance hedging strategy of Sect. 7.4 is very reminis-

cent of the path integrals used in physics [50]. This is not accidental: one

can in fact systematically derive path-integral representations for the con-

ditional probability distributions encountered in ﬁnance, introducing on the

way “Hamiltonians” [170]. The door to quantum ﬁnance has been opened.

To make the notation easier, deﬁne the log-price of an asset as x ≡ ln S,

and assume that its evolution equation is determined by a stochastic diﬀer-

ential equation

= µ

+ σε(t) . (7.39)

The relative rate of return of the asset price follows

= µ + σε(t) . (7.40)

Geometric Brownian motion follows these equations, cf. (4.53) and (4.62),

with independent ε(t) drawn from a Gaussian, and with µ

= µ − σ

/2.

The diﬀerence between both growth rates is the noise-induced drift. Here,

however, we allow the independent ε(t) to be taken from some general dis-

tribution

p(x)=



2π

izx

ˆp(z) ≡



2π

izx−H(z)

. (7.41)

For non-Gaussian probability distributions, the relation between µ

and µ is

not ﬁxed, and depends on the speciﬁc distribution considered. The charac-

teristic function ˆp(z) was introduced in (5.16), and the last identity deﬁnes a

Hamiltonian associated with this distribution. To keep consistency with Sect.

5.4, we use the variable z in the characteristic function. Analogy with physics

would suggest using p instead, but this would conﬂict with the use of p for

probabilities. For a Gaussian distribution with zero mean, the Hamiltonian

is H

= σ

/2. The Gaussian Hamiltonian describes a free particle with

mass m =1/σ

and momentum z. For a symmetric, stable L´evy distribution

7.7 Path Integrals: Integrating the Fat Tails into Option Pricing 211

with zero mean, (5.42), the Hamiltonian is H

= a|z|

, with no obvious in-

terpretation in terms of a physical system. The deﬁnition of the cumulants

in (5.17) immediately suggests the following power-series expansion of the

Hamiltonian:

H(z)=

∞



n=0

(iz)

, (7.42)

the equivalent to the cumulant expansion of the characteristic function. Two

Hamiltonians related to H(z) are useful:

H(z)=H(z) − ic

z, (7.43)

(z)=H(z) − ic

z +irz . (7.44)

The conditional probability distribution for ﬁnding x

at time t

, condi-

tioned on x

at t

, then is given by the path integral [170]

p(x



Dε



Dx exp



−



H[ε(t)]





− ε



. (7.45)

The function

H(x) is deﬁned by

H(x) ≡−ln p(x) . (7.46)

The path integral in (7.45) is evaluated by cutting the time interval into

N slices of length τ each, integrating over all x(t

), and taking the limit

N →∞,τ→ 0 with t

− t

= Nτ = const. [50]. In complete analogy to

physics, one can calculate a partition function, a generating function, and

all moments and correlation functions in the path-integral formulation. The

path integrals also satisfy a Chapman–Kolmogorov–Smoluchowski equation

(3.10), implying that they describe Markov processes. This is not surprising,

though, as we required independent increments in (7.39) from the outset.

Also, a general Fokker–Planck-type equation

∂

∂t

p(x

)=−H



−i

∂

∂x



p(x

) (7.47)

can be derived, where the canonical substitution z →−i∂

has been per-

formed in the Hamiltonian. Clearly, H(z) in general is not a quadratic func-

tion of z, and (7.47) therefore contains higher-order terms beyond the drift

and diﬀusion terms present in the canonical Fokker–Planck equation. In that

sense, (7.47) is more correctly termed a Kramers–Moyal equation, And, from

what has been said in Chap. 6, there is no equivalent Langevin equation

in this case [37, 146]. The unconditional probability distribution p(x, t) also

satisﬁes (7.47),

∂

∂t

p(x, t)=−H



−i

∂

∂x



p(x, t) , (7.48)

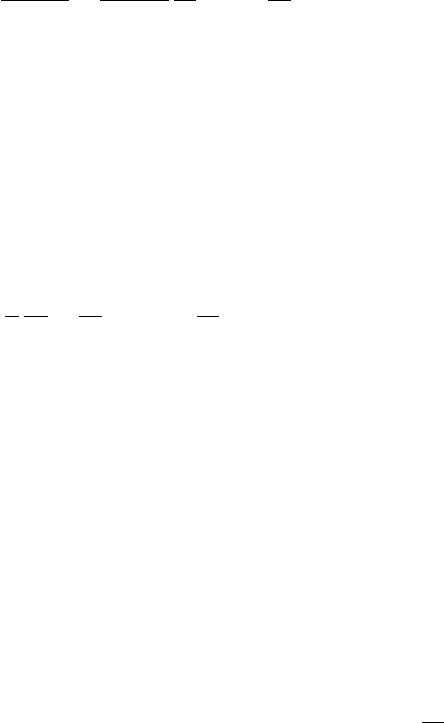
212 7. Derivative Pricing Beyond Black–Scholes

aSchr¨odinger equation in imaginary time (with a substitution p → ψ,the

illusion is complete) [170].

The stochastic processes considered here, in general, are not Itˆo processes

of the form (4.40). Therefore Itˆo’s lemma, (4.57), does not apply in the form

given there. However, one can use the Schr¨odinger equation above to derive

a generalized Itˆo relation [170]. The evolution of a function f of a stochastic

variable obeying (7.39) with increments drawn from an arbitrary probability

distribution is given by

df[x(t)]

∂f[x(t)]

∂x

−



∂

∂x



f[x(t)] . (7.49)

H appears instead of H because the ﬁrst derivative of f has been taken out

of H, cf. (7.43), to emphasize the similarity with the equivalent Gaussian

expression (4.57).

From (7.39), the relation between the stochastic variable x(t) and the

asset price is S(t)=exp[x(t)]. Using the generalized Itˆo relation, we can

relate µ

to µ by

= µ +

H(i) = µ + H(i) − iH



(0) (7.50)

and relate the log-return rate dx =dlnS to the relative return rate [170]:

−

H(i) =

− H(i) + iH



(0) . (7.51)

Integrating the expectation value of this equation from zero to t gives the

expected asset price at t,

S(t) = S(0)e

µt

= S(0) exp [µ

t − H(i) + iH



(0)] . (7.52)

Path integrals are useful for calculating expectation values of stochastic

variables, or functions thereof. As explained in Sect. 4.5.3, in an option-

pricing context, this implies that one has to use the equivalent martingale

process of the underlying, rather than the historical price process. What is

the equivalent martingale process to (7.39)? The simplest solution is

−µt

S(t)=e

−µt

x(t)

−µt

t+σ



ε(t



)

. (7.53)

A martingale distribution which gives such a process is

)=e

−µt



Dε



Dx exp



−



[ε(t)]





− ε



(7.54)

This, however, is not the only distribution with a time-independent expec-

tation value. There is an entire family of equivalent martingale distributions

with this property, among them

7.7 Path Integrals: Integrating the Fat Tails into Option Pricing 213

)=e

−rt



Dε



Dx exp



−



[ε(t)]





− ε



(7.55)

This distribution is also called the natural martingale [170].

The application to option pricing now uses a diﬀerential equation for the

wealth of a portfolio consisting of N

(t) assets of price S(t), N

(t) options

of price f(t), and N

(t) units of a risk-free bond (or cash) of price B(t). The

aim is to determine a hedging strategy {N

(t),N

(t)} which makes

the portfolio

Π(t)=N

(t)S(t)+N

(t)f(t)+N

(t)B(t) (7.56)

grow exponentially without ﬂuctuations:

dΠ(t)

= r

Π(t) . (7.57)

The risk-free position B(t) grows with the risk-free interest rate r. The ab-

sence of arbitrage then implies that

= r. (7.58)

As in the Black–Scholes theory, in the absence of transaction costs, the trad-

ing strategy is self-ﬁnancing, i.e., there is no net cash ﬂow into or out of the

portfolio. This is expressed by

(t)

S(t)+

(t)

f(t)+

(t)

B(t)=0. (7.59)

Injecting this equation into (7.57) cancels the terms involving the bond (which

is why cash or bonds did not appear in our discussion of the Black–Scholes

theory). Rewriting all remaining contributions in terms of the option price

f(t) and its derivatives, and in terms of the log-price x(t), the ∆-hedge of

Black and Scholes is found by requiring that the ﬂuctuating variable dx/dt

must disappear from the equations. At the same time, the option price sat-

isﬁes the Fokker–Planck-type equation

∂f

∂t

= rf −



r +

H(i)



∂f

∂x



∂

∂x



. (7.60)

This is a straightforward generalization of the Black–Scholes equation (4.75),

as can be checked by using the quadratic Hamiltonian H

gBm

= σ

/2of

geometric Brownian motion. The general solution of this equation is

p(x

)=e

−r(t

−t

)



∞

−∞

2π

iz(x

−x

)−

[

H(z)+i{r+

H(i)}z

]

−t

]

(7.61)

214 7. Derivative Pricing Beyond Black–Scholes

This equation, however, must be solved numerically. Unfortunately, no ex-

amples have been worked out to date which would demonstrate the potential

power of the method [170].

Path-integral techniques can also be useful when path-dependent options

are priced and hedged [171]. Examples of path-dependent options are Asian,

barrier, or lookback options. The payoﬀ of an Asian option usually is deter-

mined by the average of the price of the underlying during a certain period

[10]. The payoﬀ of a barrier option is triggered by the underlying passing

above or below a certain threshold price. The payoﬀ of a lookback option

depends on the maximal or minimal stock price realized during the lifetime

of the option. For a European call it is the diﬀerence between the maximum

and the minimum of the price of the underlying while, for a European put, it

is the diﬀerence between the maximal price and the price at maturity of the

underlying stock. The general ideas are somewhat similar to the preceding

presentation, which is why we will be rather brief here.

Assume that we know the risk-neutral stochastic process of the under-

lying, and assume further (for simplicity, this is not a requirement) that it

follows geometric Brownian motion. Then the price f of a path-dependent

option at maturity is

f[S(T ), I,T]=h[S(T ), I]=h[e

x(t)

, I] , (7.62)

where h[...] is the payoﬀ proﬁle of the option, and the path-dependent ran-

dom variable

I =



dsw(s) g[x(s),s] (7.63)

is written as an integral over an arbitrary function g with a sampling function

w(s). For continuous sampling w(s) = 1 while, for discrete sampling, w(s)

is a series of delta functions. In a risk-neutral world, the option price is the

discounted expectation value of the payoﬀ

f[S(t),t]=e

−r(T −t)

h[e

x(T )

, I]

(7.64)

−r(T −t)



∞

−∞

dx(T )



∞

−∞

dI p[x(T ), I|x(t)] h[e

x(T )

, I ]. (7.65)

From the preceding discussion, it is obvious that the conditional proba-

bility distribution can be represented as a path integral (given here for the

special case of geometric Brownian motion)

p[x(T ), I|x(t)] =

2π

exp



µ{x(T ) − x(t) − µ(T − t)}





∞

−∞

dke

−ikI

K[x(T ),x(t); T − t] , (7.66)

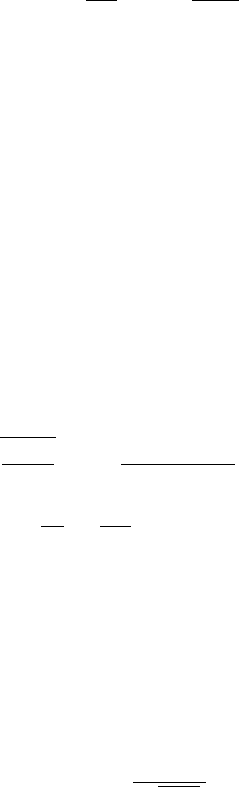
7.7 Path Integrals: Integrating the Fat Tails into Option Pricing 215

K[x(T ),x(t); T −t]=



x(T )

x(t)

Dx(s)exp



−

2σ





dx(s)

+ V [x(s),s]



(7.67)

V [x(s),s]=−2ikσ

w(s) g[x(s),s] . (7.68)

K[x(T ),x(t); T −t] is a propagator, and the path integral in (7.67) integrates

over all paths connecting x(t) at the initial time t with x(T )atmaturityT .

V [x(s),s] is a potential whose shape is determined by the path-dependent

random variable I.

These path integrals, and the corresponding option prices, cannot be

evaluated analytically in general. Matacz [171] has shown, however, that a

partial average can be performed systematically based on the path-integral

representation, which considerably reduces the numerical eﬀort compared

to standard numerical methods such as Monte Carlo. The path integral in

K[x(T ),x(t); T −t] is evaluated by discretizing time and deriving a cumulant

expansion for the propagator (s = t + n,  =(T − t)/N ):

K[x(T ),x(t); T − t]=



∞

−∞

N−1

...dx

n=1

K[x

n−1

; ] , (7.69)

K[x

n−1

; ]=



2πσ



exp



−

− x

n−1

)

2σ



∞



m=1



−



2σ



n−1

; )

. (7.70)

Notice that the path dependence of the option has entirely been transformed

into the details of the cumulants. The cumulant expansion at the same time

is a power-series expansion in , the length of a time slice. A partial averaging

of the short-time propagator K[x

n−1

; ] can then be performed by simply

truncating the cumulant expansion at some order. For example, a propagator

correct to second order in  is obtained by dropping all cumulants beyond

the ﬁrst. The ﬁrst cumulant is given by

n−1

; ]=−i2σ



dτw(τ)



∞

−∞

−p

/2ν



2πν

g[¯x

+ p

,τ] (7.71)

with the abbreviations ν

= σ

(1 − τ )τ,¯x

= τ(x

− x

n−1

)+x

n−1

,and

τ =(s − s

n−1

)/. If required, higher-order terms can also be calculated.

The option price ﬁnally becomes in this ﬁrst-order cumulant approxima-

tion

f[S(t),t]=e

−r(T −t)



∞

−∞

...dx

p[x

,...,x

]

×h

, 2σ





n=1

n−1

; )

+ .... (7.72)

216 7. Derivative Pricing Beyond Black–Scholes

Often, the ﬁrst cumulant can be calculated analytically. Within our approxi-

mation of geometric Brownian motion, it is simply the Gaussian transform of

the function g containing the path dependence of the option. An important

practical advantage is that the size  of the time slices entering the partially

averaged cumulants can be chosen much bigger than the sampling scale of the

options, which determines the structure of the sampling function w.Thisis

an important simpliﬁcation in the evaluation of the multidimensional integral

in (7.72), which can be evaluated by standard Monte Carlo methods [171].

Again, however, no benchmark examples are provided which would allow for

a critical assessment of the virtues and drawbacks of this method.

Another perspective is opened up by applying directly numerical meth-

ods to the Lagrangian (or Hamiltonian) which is generated by a path-integral

formulation of the conditional probability distribution functions [172]. One

such method is simulated annealing, which is an extension of a Monte Carlo

importance sampling method. The aim is to ﬁnd the global minimum of a

ragged energy landscape. To this end, simulated annealing works at ﬁnite

temperature. The process is started at high temperature, and the temper-

ature then is lowered in order to trap the system in an energy minimum.

Normally, this minimum will not be the global but rather a local minimum.

In order to ﬁnd the global minimum, the system is reheated and recooled

in cycles. In ﬁnance, the equivalent of the ragged energy landscape would be

stochastic volatility. The global minimum dominates the evolution of the con-

ditional probability density with time. Once it has been calculated from the

path-integral representation, one again we can use it for expectation-value

derivative pricing in a risk-neutral world.

7.8 Path Integrals: Integrating Path Dependence

into Option Pricing

It is surprising that less work has been done on the use of path integrals to

incorporate path dependences into option theory. The most prominent exam-

ple of path-dependent options are the plain vanilla American-style options.

Depending on the actual path followed by the price S(t) of the underlying,

early exercise may or may not be advantageous [10]. In Sect. 4.5.4, we have

discussed that the correct pricing of American options requires approximate

valuation procedures even when the price of the underlying follows geometric

Brownian motion. Some of them certainly can be improved. Exotic options

with path-dependent payoﬀ proﬁles are other examples where the methods

described in the following can be useful.

The central problem in pricing path-dependent options is the evaluation

of conditional expectation values such as those used on the right-hand sides

of (4.100) and (4.101). We can write them in the general form

7.8 Path Integrals: Integrating Path Dependence into Option Pricing 217

h[S(t)] | S(t



) =



∞

−∞

dxh



x(t)



q(x, t | x



) . (7.73)

The notation x =lnS has been kept from above. q(x | x



), where explicit

time variables are dropped from now on, is the transition probability of the

log-price between times t



and t. h(S) is the payoﬀ function of the option

taken at price S of the underlying. From our earlier discussions, there are a

few indications that path integrals could be useful in evaluating the transition

probability q(x | x



), and expectation values involving this quantity: (i) In

Sect. 4.5.2, we saw that path integrals led to a quantum Black–Scholes Hamil-

tonian (4.93) for the European options with the standard solution [51]. (ii)

The Fokker–Planck equation employed in Chap. 6 also admits a path-integral

representation [37]. The transition probabilities q(x | x



) only depend on the

stochastic process involved and not on the speciﬁc option considered. Option

properties only enter through the expectation values (7.73).

By iterating the Chapman–Kolmogorov–Smoluchowski equation (3.10),

and discretizing time between t



and t into n + 1 slices of length ∆t =(t −



)/(n + 1), we write the transition probability as [173]

q(x | x





∞

−∞

...



∞

−∞

...dx



(2πσ

∆t)

n+1

× exp



−

2σ

∆t

n+1



k=1



− x

k−1

−



r −



∆t



. (7.74)

Formally, we set x = x

n+1

and x



= x

. A direct evaluation of q(x | x



)

by Monte Carlo simulation requires very long simulation times when good

accuracy is sought. On the one hand, by taking the continuum limit, one can

derive a path integral representation [173]

q(x | x







−1

˜x



exp



−





dτL



˜x(τ),

dτ

; τ



(7.75)

with a Lagrangian



˜x(τ),

dτ

; τ



2σ



dτ

−



r −



(7.76)

equivalent to the Black–Scholes Hamiltonian (4.93).

On the other hand, one can use substitutions common in the evaluation

of path integrals to transform (7.74) into a form which allows a fast and

accurate Monte Carlo evaluation. Two steps are necessary to overcome two

important obstacles in the evaluation of (7.74) or (7.75). Firstly, the integral

kernels are nonlocal in time: (7.74) depends on the diﬀerence x

− x

k−1

and (7.75) on dx/dτ. An expression local in time would allow to separate

the multi-dimensional resp. path integral into a product of independent one-

dimensional integrals. Secondly, the integral should be brought into a form

218 7. Derivative Pricing Beyond Black–Scholes

which allows a Monte Carlo evaluation which is fast and accurate at the

same time. As discussed in Sect. 4.5.4, the convergence of a direct Monte

Carlo evaluation is rather slow. One therefore seeks a representation of the

integral where Monte Carlo simulations give a good convergence.

The ﬁrst goal is achieved by the substitution

= x

− k



r −



∆t (7.77)

which eliminates the drift term in (7.74). The argument of the exponential

in (7.74) is transformed

n+1



k=1



− x

k−1

−



r −



∆t



n+1



k=1

− y

k−1

]

= y

· M · y +



− 2y

+ y

n+1

− 2y

n+1



. (7.78)

=(y

,...,y

) is the transpose of y,andM is a tridiagonal matrix which

can be diagonalized by an orthogonal matrix O with eigenvalues m

and

eigenvectors w

. We obtain for the transition probability

q(x | x



−(y

n+1

)



(2πσ

∆t)

n+1

i=1



∞

−∞

exp



−

2σ

∆t



i=1



−

+ y

n+1

)



−

+ y

n+1

)

-6

(7.79)

The coupled, multi-dimensional integral over the x

, resp. y

, now is decou-

pled into a product of one-dimensional integrals over the w

-variables with a

Gaussian kernel.

A naive Monte Carlo integration of the integral over w

uses uniformly

distributed random numbers w

, and determines the value of the integral as

the product of the average of the kernel at the positions w

times the area

sampled [174]. The error depends on the standard deviation of the kernel at

the positions w

, and decreases as the inverse square root of number of w

This is the problem of slow convergence. The problem will be computationally

more eﬃcient if we can transform to a structure where the kernel is constant

(or almost constant), and the random numbers are no longer distributed

uniformly. This technique is known an importance sampling [174] and, for

our kernel, is achieved by the substitution



2πσ

∆t

exp



−

2πσ

∆t



−

+ y

n+1

)



(7.80)

7.8 Path Integrals: Integrating Path Dependence into Option Pricing 219

The resulting transition probability

q(x | x



−(y

n+1

)



(2πσ

∆t)

n+1

i=1



∞

−∞

(7.81)

× exp



−

2σ

∆t

+ y

n+1

)



possesses the desired features: A constant kernel the integral which – in Monte

Carlo – is sampled by random numbers h

drawn from a Gaussian with mean

+ y

n+1

)

and variance σ

∆t/m

[173]. With these transforma-

tions, the asset price is given by

=exp





k=1

+ i



r −



∆t

. (7.82)

The normal distribution of the h

implies the log-normal distribution of the

prices S

, as required for geometric Brownian motion. This simple represen-

tation of the price in terms of the random sampling variables h

makes this

method well suitable for evaluating path-dependent options.

This path intergral representation and its discretized counterpart trans-

formed as above, are useful for several purposes.

• Firstly, it is a competitive alternative, both in terms of accuracy and calcu-

lation speed, to ﬁnite diﬀerence methods, to binomial trees, and to Green

function methods [173].

• Secondly, for American options, the continuum limit in time, ∆t → 0, can

be combined with an “inﬁnitesimal trinomial tree” in the space of the log-

prices, x

, to allow a seminanalytical evaluation of the fundamental integral

(7.73). Speciﬁcally, noting that the transition probability, for small ∆t,isan

almost δ-function peak in x

−x

k−1

, the payoﬀ function h(e

) is expanded

to second order on the trinomial tree x

= x

k−1

+ r∆t + jσ

√

∆t with j =

−1, 0, 1. The integral (7.73) is evaluated analytically with the second-order

expanded payoﬀ function, and the second-order coeﬃcient is determined by

numerical diﬀerentiation on the trinomial tree. The implementation of this

scheme makes almost negligible the numerical eﬀort of calculated prices

and hedges for American options (for geometric Brownian motion) [173].

• The path integral representation can be generalized to path-dependent op-

tions on assets following multidimensional, correlated geometric Brownian

motion. Examples include options dependent on baskets of stocks, or bas-

kets containing stocks, bonds, and currencies. Often, the statistical prop-

erties of the basket price are less well known than those of the constituent

assets. Path-dependent exotic options on such baskets can be evaluated by

generalizing the techniques described above [175].