Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged
Подождите немного. Документ загружается.

160 Johannes Bl¨omer
secured with several padlocks, one for each member of the committee. Every
member of the committee has the key to one of the padlocks. To open the safe
and publish the document every member has to unlock her padlock, thereby
agreeing to the publication of the document.
With secret sharing we can also guarantee that the document is published
only if all members of the committee approve the publication. To do so, we
secure the safe, not with padlocks that require a key, but instead with a
single combination lock, whose secret combination consists of, say, decimal
digits. The secret combination is divided into several pieces, one piece for each
member of the committee, and every member of the committee gets her own
piece of the secret combination, that is, her own partial secret. If all members
of the committee agree to the publication of the document, they combine their
partial secrets to retrieve the secret combination, open the safe, and publish
the document. The partial secrets of the committee members are like keys for
different padlocks that secure the safe. This example demonstrates how we
can use secret sharing to replace physical keys by secret information.
In addition to sharing the secret combination of a safe, there are many
other applications of secret sharing. In fact, secret sharing is one of the most
important techniques in cryptology, the science of encrypting messages, or,
more generally, the science of securing information against unauthorized access
and modification. If we combine methods to share a secret with public-key
cryptography (see Chap. 16), then we can replace keys as well as safes and locks
by secret information and algorithms. Using such a combination of methods
we can encrypt data in such a way that, like in our example above, documents
can be recovered or decrypted only if all committee members contribute their
shares of the secret. Here the partial secrets are parts of a public key in a
public-key encryption scheme.
A Simple Method to Share a Secret
So far we have not described methods to share a secret. How can we replace
locks and keys by partial secrets, each of which is known to a single committee
member? To discuss the first idea, we return to our document locked in a safe
that is secured by a combination lock with a 50-digit secret combination. Let
us assume that the secret combination is
S = 65497 62526 79759 79230 86739 20671 67416 07104 96409 84628.
Let us also assume that our committee has ten members. Therefore, we want to
partition our secret S into ten partial secrets such that only all ten committee
members together are able to reconstruct the secret S. What about giving each
committee member 5 of the 50 digits of our secret combination S (Fig. 17.1).
You can see immediately that this is not such a great idea. If 9 out of
10 committee members decide that they want to publish the document, they
already know 45 of the 50 digits of the secret combination necessary to open

17 How to Share a Secret 161
Fig. 17.1. A simple example of how to share a secret
the safe. However, remember that we want that even nine committee members
together can learn little or nothing about the secret S. But with our simple
idea, once 9 out of 10 committee members collaborate, each of them all at
once knows 45 digits of S instead of the 5 digits each of them individually
knew before they collaborated. We can put this differently. Before the collab-
oration each committee member had to try 10
45
possible combinations for the
45 digits they did not know. By collaborating, the nine committee members
who exchange their parts of the secret combination reduce the number of pos-
sible combinations they have to try to determine the secret S to 10
5
= 100000
combinations. To appreciate the information gain the 9 collaborating com-
mittee members achieve, let us assume that a single person can check in one
second whether a given 50-digit number is the secret combination for the safe.
To try all 10
5
possible combinations for the 5 digits that are still unknown,
the 9 collaborating committee members require roughly 3 hours. This follows
from the fact that a single hour has 3600 seconds; hence in an hour 3600
possible combinations for the safe can be tested. We see that within a rela-
tively short time the nine collaborating committee members can determine
the secret combination of the safe, open it and publish the document even
without the consent of the tenth committee member. Now let us consider how
much time it takes a single committee member, who knows only 5 of the 50
digits of the secret combination, to try out all 10
45
possible combinations for
the digits she does not know. Assuming again that it takes a second to test
a single combination, a simple calculation shows that a single member will
need roughly 10
35
years to determine the secret combination. Physicists tell
us that the universe has not existed for this long, and that in all likelihood
it will cease to exist well before a single committee member will be able to
determine the complete secret combination.
So, let us try a different technique that brings us much closer to our ulti-
mate goal of sharing secrets. In this method we distribute our secret S among
the ten committee members by choosing ten random numbers larger than zero
that add up to S. These numbers are the partial secrets that are given to the
ten committee members. Let us look at a small example. In this example the
secret S is a natural number, and the partial secrets are numbers between 1
and 50. To simplify the example, we want to share or distribute the secret
among four people rather than the ten committee members from our previous
example. Assume the secret S is 129. Then the partial secrets may be chosen
162 Johannes Bl¨omer
as 17, 47, 31 and 34, since 17 + 47 + 31 + 34 = 129. It is clear that if all
four people owning a partial secret collaborate then they can reconstruct the
secret S; they simply have to add up their partial secrets. But again we have
a problem: All participants know that the partial secrets lie between 1 and
50. Hence, even before receiving their shares the participants know that the
secret S lies between 4 and 200. Now assume that the first three participants
join forces to gain information about S. To do so, they simply add up their
partial secrets and obtain 17 + 47 + 31 = 95. Now they know that S will be a
number between 95 + 1 = 96 and 95 + 50 = 145, since the fourth participant
also received a partial secret between 1 and 50. The number of possible values
for S has dropped from almost 200 to 50, and the three colluding participants
have gained a lot of information about S. But a simple trick helps us modify
the method in such a way that a proper subset of participants will not gain
any information about the secret S even if they exchange all their partial
secrets. The trick is to use division with remainder.
The new method works as follows. We assume that the secret S that we
want to share among a certain number of participants is a natural number
between 0 and some really large number N. In our example with the document
stored in a safe secured with a 50-digit secret combination, the number N will
be 10
50
. To work with concrete numbers, let us assume again that we want
to share a secret value among ten participants. But once you understand the
method you realize that with this method we can share a secret among an
arbitrary number of participants. To share the secret S we proceed in two
steps.
1. First we choose nine random numbers between 0 and N − 1. Let
us call these numbers t
1
,t
2
,...,t
9
. These numbers are the partial
secrets for the first nine participants.
2. To determine the tenth partial secret t
10
, first we compute t
1
+ ···+
t
9
and divide this sum by N. However, we perform division with
remainder and are only interested in the remainder R.Nextwelook
at the difference S − R. If S − R is positive, then t
10
is S − R.If
S −R is negative, then t
10
is S −R + N. With this recipe we get that
the secret S is the remainder if we divide t
1
+ t
2
+ ···+ t
10
by N.
To illustrate this method let us look at a simple example, where all numbers
are small enough to compute them by hand. We choose N = 53, and we want
to share the secret S = 23 among four people.
1. We choose the first three partial secrets. Let these be 17, 47 and 31.
2. To determine the fourth partial secret, first we compute the sum of the
first three secrets, 17 + 47 + 31 = 95. We divide 95 by 53 and obtain
remainder R = 42. Since S − R =23− 42, which is negative, the fourth
partial secret is 23 − 42 + 53 = 34.
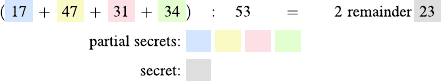
17 How to Share a Secret 163
Fig. 17.2. Example for secret sharing by division with remainder
You can also follow this example in Fig. 17.2.
Does this method really satisfy our requirements? Let us look at our simple
example. If the four owners of partial secrets collaborate they can compute
the sum of their partial secrets. The secret S is then simply the remainder if
they divide the sum by N = 53. In our case, the sum is 129, and the remainder
after division by 53 is 23, the secret. You can easily verify that the approach
works not only in our simple example but in general.
What happens if not all participants collaborate? Can a proper subset
of the participants determine the secret S or gain significant information
about S? At first glance it might seem that we treat the last participant
differently from the remaining participants, since her partial secret depends
on the other partial secrets. However, if we take a more careful look we realize
that this impression is misleading. Let us go back once more to our simple
example, and let us look at the first partial secret, 17. The sum of the partial
secrets excluding 17 is 47 + 31 + 34 = 112. Then x = 17 is the unique number
x such that 23 is the remainder of dividing 112 + x by 53. We see that the
first partial secret 17 depends on the remaining partial secrets in exactly the
same way that the last partial secret 34 depends on the remaining partial
secrets.
We still have not answered the question of what happens if a proper sub-
group of participants tries to determine the secret from its set of partial se-
crets. Phrased differently, the question becomes: Do we really need all partial
secrets to determine the secret? Again, we first look at our example. Assume
that the last three participants with partial secrets 47, 31 and 34 try to de-
termine the secret, or more modestly try to gain some information about the
secret. Of course, we assume that they know the number N = 53, but they
do not know the partial secret of the first participant. They also know the
method we use, so they know that the secret is the remainder we get by di-
viding the sum of the partial secrets by 53. Now they can compute the sum
of their partial secrets, which is 112. Dividing this number by 53 gives the
remainder 6. Had the first partial secret been 0 instead of 17, then the overall
secret would have been 6 instead of 23. A first partial secret of 1 would have
led to the secret 7. And so on, until the possible first partial secrets 51 and
52, which would have led to secrets 4 and 5, respectively. More precisely, for
every number s between 0 and 52 there is a number t such that the sum of
121 and t has remainder s when divided by 53. This means that with first
partial secret t the overall secret would have been s instead of S = 23. This, in
turn, implies that if the last three participants knew their own partial secrets
164 Johannes Bl¨omer
they cannot exclude a single value for the overall secret. Summarizing, we can
say that the last three participants together do not learn anything about the
secret from their partial secrets. You can easily check that this is not only
true for our simple example, but that it is correct in general.
However, you have to ensure that your numbers are not too small. In our
example with N = 53 it is certainly not very difficult to try all possible values
for the missing partial secret. After all, there are just 53 possible values. Even
simpler, since the secret itself can take on just 53 values, you can to try all
possible values for the secret without knowing or taking into account any
partial secrets. In applications of secret sharing therefore one chooses much
larger values for N . For example, you may take N =10
50
. With this choice,
there are 10
50
possible values for a partial secret of the secret itself. As we
have seen before, in this case it is unrealistic to simply try out all possible
values for a partial secret.
General Secret Sharing
So far we have considered only the situation where all recipients of partial
secrets must collaborate to recover the secret. Now we want to look at a more
general situation in which any sufficiently large number of recipients of partial
secrets together can reconstruct the secret.
Let us begin with the simple case where any two out of three recipients of
partial secrets should be able to recover the secret. However, a single recipient
of a partial secret should not be able to reconstruct the secret or gain a lot
of information about the secret. In this case, representing the secret as the
sum of partial secrets, the idea that was so successful in our scheme above,
will not get us very far. We need a new idea, and a little geometry will help
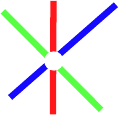
us. Let our secret be a point P in the plane. We can imagine that the two
coordinates of point P constitute the secret combination of a safe. We also
choose three lines in the plane that meet in point P . The three lines are the
partial secrets. We have illustrated this idea in Fig. 17.3. Now if any two out of
the three recipients of partial secrets collaborate they can simply compute the
intersection point of the lines that constitute their partial secrets to compute
the overall secret. You can see this in the three pictures in Fig. 17.4.
Fig. 17.3. Three lines that intersect in a point. The intersection point is the secret
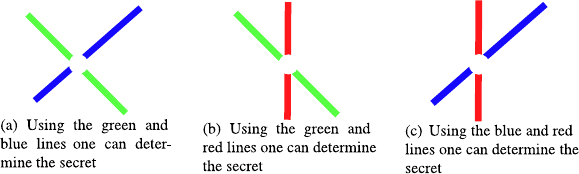
17 How to Share a Secret 165
Fig. 17.4. Secret sharing in the plane
What does a single participant learn about the secret from her partial
secret? Clearly, she learns something. Before receiving her partial secret she
only knew that the secret is some point in the plane. After seeing her partial
secret she knows the secret lies on the line that is her partial secret. So, she
definitely has learned something, but she still does not know the secret.
We can easily generalize this method such that any two out of m recipients
of partial secrets can reconstruct the secret from their partial secrets. To do
so, the secret is again a point P in the plane. But instead of three lines that
intersect in P we choose m lines that intersect in P . Every one of theses lines
is a partial secret.
What about the case that any three recipients of partial secrets must be
able to compute the secret? In this case we leave the plane and enter (three-
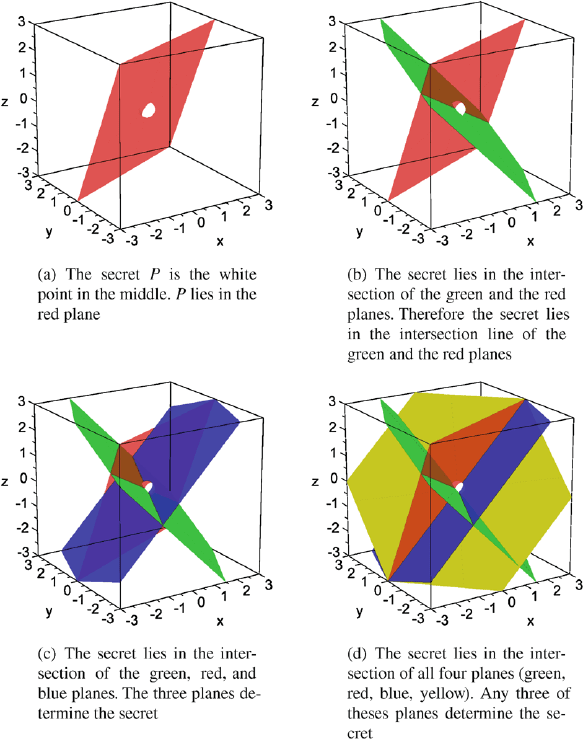
dimensional) space. Again, our secret is a point P; this time, however, it is a
point in the three-dimensional space. As partial secrets we choose planes in
the space such that any three of these planes intersect in point P .InFig.17.5
you can see this for four partial secrets.
Any three of our recipients of partial secrets can reconstruct the secret by
computing the intersection of the three planes they received as partial secrets.
You can see this nicely in Fig. 17.5(c). However, if fewer than three partici-
pants collaborate they also learn something about the secret. For example, if
two recipients of partial secrets work together they can compute the line in
which their two planes intersect. You can observe this by looking at the red
and green planes in Fig. 17.5(b). If the recipients of the red and green planes
combine their partial secrets, they can deduce that the secret must lie on the
intersection line of the red and green planes. However, they still have no clue
which point on this line is the secret.
Secret Sharing, Information Theory and Cryptography
Of course, we can further generalize our problem and ask whether it is possible
to share a secret S among m people such that any t (or more) of these people
are able to reconstruct the secret, whereas fewer than t people are not able to
reconstruct the secret, or more stringently, do not gain a lot of information
166 Johannes Bl¨omer
Fig. 17.5. Secret sharing in space
about the secret S. As it turns out, for any combination of m and t this
is possible and is called t-out-of-m secret sharing. One way to realize such
general secret sharing schemes is by generalizing the geometric constructions
that we discussed above. To obtain a t-out-of-m secret sharing scheme one
hastogotot-dimensional spaces.
There are even constructions for t-out-of-m secret sharing in which fewer
than t people learn absolutely nothing about the secret. These schemes do not
rely on geometry; instead they use so-called polynomials. This construction
was invented by Adi Shamir, a famous cryptologist, and therefore it is called
Shamir’s secret sharing scheme.
17 How to Share a Secret 167
Who computes and distributes the partial secrets? So far we have com-
pletely ignored this question. Obviously, this is an important question. Who-
ever computes and distributes the partial secrets must know the secret. If one
applies secret sharing schemes, you usually have to assume that a trustworthy
person exists who computes and distributes the partial secrets. One can think
of this person as a completely trustworthy and incorruptible referee.
What exactly do we mean, if we say that someone has gained informa-
tion? What is information? Somehow we all know what information is. But
if we want to deal with information in a precise mathematical sense, as we
want in secret sharing, then we have to be more precise. Once you under-
stand the secret sharing methods that we presented above, you will be able
to define concepts like information and information gain in a precise math-
ematical manner. For example, partial shares reveal no information about
the overall secret if knowing the partial shares does not reduce the number
of possible values for the secret. In 1948 the famous mathematician Claude
Shannon used these ideas to found information theory as a branch of mathe-
matics.
We can go even further. Information that we can gain in principle but
only by spending an unreasonable amount of time like 10
35
years is useless.
Secret sharing provides a good example. No matter how we share the 50 digit
secret combination of a safe among 10 members of a committee, in princi-
ple it is possible to determine the secret combination by trying all possible
10
50
combinations. But in practice this is not a viable option. The number
10
50
is so enormous that even with the help of a computer, we cannot try
all 10
50
possible secret combinations. Therefore, we can say that a secret
cannot be revealed if determining the secret simply takes too much time to
be practically feasible. These considerations lead us way beyond information
theory. They lead to questions about how many resources are needed to com-
pute something or to gain some information. In this book you can learn,
for many interesting problems, like multiplying large integers (Chap. 11),
how much time is required to solve them. On the other hand, in the chap-
ter about public-key cryptography (Chap. 16) or about one-way functions
(Chap. 14) you also see that sometimes it is very useful if a problem can-
not be solved efficiently or if it is impossible or very difficult to gain certain
information.
Further Reading
1. Chapter 16 (Public-Key Cryptography)
In many applications the secret keys of public-key encryptions schemes as
described in this chapter are not given to a single person. Instead, using
secret sharing techniques, secret keys are distributed among a group of
people. In this way you can avoid situations in which the secret key of a
large cooperation is owned by a single person.

168 Johannes Bl¨omer
2. http://en.wikipedia.org/wiki/Secret sharing
In this article you will find (sometimes longer) descriptions of the tech-
niques that we discussed.
3. Wade Trapp and Lawrence Washington: Introduction to Cryptography.
Pearson Education International, 2nd edition, 2006.
If you want to learn more about secret sharing this book is a good starting
point. Of course, the explanations in this book are much more detailed
and technical than we were able to give in this short chapter.

18
Playing Poker by Email
Detlef Sieling
Technische Universit¨at Dortmund, Dortmund, Germany
In this chapter we explore how to play card games like poker without a meet-
ing of the players. Instead, the cards are distributed using email or snail mail.
Different from commercial online poker systems, the cards are shuffled and
distributed by the players. There is no extra dealer who the players have to
trust. Obviously, there are some difficulties: The player shuffling and distribut-
ing the cards has to do this without gaining any knowledge of the cards he is
distributing, while he has to send emails with information about those cards.
Furthermore, this player must not distribute any card more than once, while
he must not know which cards have already been distributed. Finally, if any
player cheats, the other players should be able to detect this.
Dealing Cards by Snail Mail
In order to collect ideas on how to play card games by email, we first try
to do this by snail mail. We first look at the case of two players, who are
called Alice and Bob. They are at different places and are thus not able to
observe each other. Then each player can easily cheat by using a second deck
of identical cards. From those cards, he can select a good hand, e.g., a royal
flush. In order to make this impossible, each card of the deck in use will have
a seal indicating that this card is really from the deck in use and not from
some other deck.
How to Shuffle and Distribute the Cards
For our poker game we use a card deck with the 52 cards club-ace, club-two,
..., diamond-king. After shuffling the cards each player has to get five cards.
How is it possible for one player to shuffle and distribute the cards without
gaining any information on the cards given to the other player? We do this
with envelopes. Bob puts each of the 52 cards into a separate yellow envelope.
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0
18,
c
Springer-Verlag Berlin Heidelberg 2011
