Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged
Подождите немного. Документ загружается.

150 Dirk Bongartz and Walter Unger
The public and the private key
p private key
11 public factor
143 public product
For you it is easy to compute the private key because you are able to do
a division. The private key is p = 143/11 = 13. In our limited mathematics,
however, this private key stays secret.
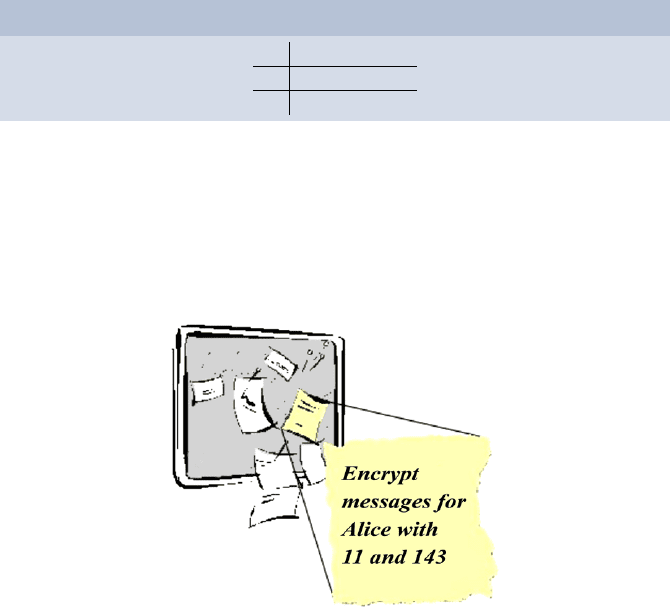
At the bulletin board of the school Alice posts the following note for ev-
erybody to read. However, nobody is able to do divisions. Thus the private
key of Alice stays secret.
Encryption
Bob, who wants to send a message to Alice, also reads this note. Assume
the message is to contain the date of the next party at Bob’s home, which
is December, 5th. The message is the number 5 because it is already known
that the party takes place in December.
Bob encrypts the message as follows. He knows the messages 5 and the
public key of Alice, that is, the numbers 11 and 143.
Bob thinks up a fourth number; this number is called sending secret.Using
this sending secret he computes the encrypted data. This encrypted data
consists of two numbers, the encrypted message and the decryption help.
Bob computes the product of the sending secret and the public product
of Alice. The encrypted message is computed by adding the message to this
product. If we assume that Bob chose 3 as the sending secret; then, the en-
crypted message is 5 + 3 · 143 = 434. This number, 434, is published, but the
number 3 has to be kept secret. Otherwise everyone could reconstruct the
message by computing 434 − 3 · 143 = 5.
16 Public-Key Cryptography 151
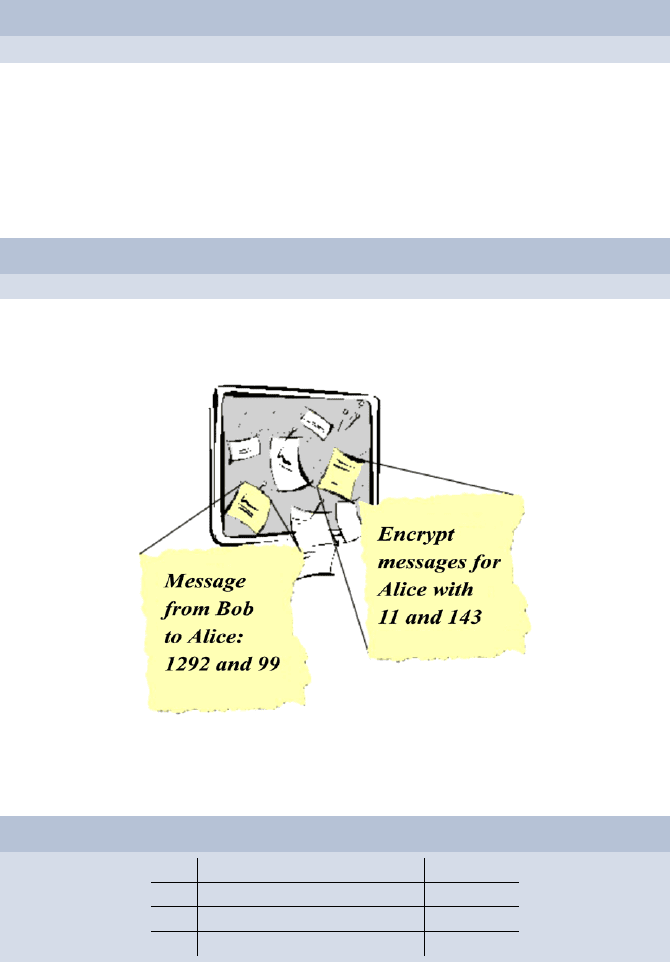
Since we revealed the sending secret, we have Bob choose another one,
called s, and he doesn’t tell what the value is. Bob computes the secret mes-
sage:
Computing the secret message
5+s · 143 = 1292
The 1292 becomes public, while s is kept secret.
As long as only Bob knows the sending help, no one will be able to decrypt
this message. But how can Alice find out what the message is? In order that
only Alice be able to decrypt the 1292, Bob provides as decryption help the
product of the sending help and the public factor of Alice.
Bob computes 11 · s = 99. This number is made public as well.
Computing the decryption help
11 · s =99
Bob places the following note at the bulletin board of the school.
Thus, everyone knows the following numbers because everyone can read
the two notes at the bulletin board.
Numbers known publicly after encryption and posting
11 public factor from Alice
143 public product from Alice 11 · p
1292 encrypted message 5+s · 143
99 decryption help s · 11

152 Dirk Bongartz and Walter Unger
Even if everyone knows the computation steps of Bob, without division it
is impossible to compute the sending secret or the private key. And without
the sending secret it is impossible to find out what Bob’s message was.
Decryption
Now Alice decrypts the message from Bob. Like the others, Alice can not do
divisions. However, Alice knows her private key. Let us take a closer look at
the encrypted message.
The encrypted message
1292 message + sending secret · 143
= message + sending secret · public product
= message +
sending secret · public factor · private key
= message + decryption help · private key
Alice can obtain the message by the following calculation.
Decryption
1292 − 99 · (private key p)=5
As you can see, Alice did not need division for this calculation.
The Eavesdropper
In espionage movies we see how spies eavesdrop on calls and other conversa-
tions. Often, secure connections are used to prevent this. How can we make
sure that these connections are really secure?
For our little message from Bob to Alice we did not need any secure con-
nection. All communication was done publicly by using the bulletin board of
16 Public-Key Cryptography 153
the school. An eavesdropper who cannot do division cannot decrypt the mes-
sage. It is kept private as long as Alice and Bob do not each reveal a secret
number. Furthermore, it was not necessary for Alice and Bob to meet before.
This is the main advantage of this system compared to the one-time pad from
Chap. 15.
Without Limited Mathematics
Our system is secure as long as no one is able to do divisions. However, all of
us have learned at school how to do divisions.
If you have read the previous chapters of this book carefully, you may
have noticed that by using one of the previous methods a division could be
achieved very fast (see Chap. 1). To compute the fraction a/b one may simply
guess a candidate c between 0 and a for given natural numbers a and b. Then,
one checks whether b ·c really equals a. If the result is bigger than a, a smaller
value for c must be the true one. If the result is smaller than a, it has to be the
other way around. Applying this idea repeatedly, always choosing the median
of the remaining interval (i.e., performing a binary search), we get the result
very fast.
This method uses the fact that the fraction a/b becomes smaller when b
gets larger. Otherwise, binary search would not be applicable.
A binary search will fail, however, if our calculus is based on residues. The
mathematical background for modular arithmetic is explained below. Since a
division is still efficiently computable for residues, we also have to replace the
division by something else.
ElGamal’s Method
There are (many) more operations in mathematics than just the basic arith-
metic operations. We cleverly choose new operations that are easy to perform,
and use them to replace addition, subtraction, and multiplication in our prim-
itive system from above. The operations are the following.
• Instead of addition we use modular multiplication. (Modular multiplication
is a multiplication on residues. See also the algorithms from Chap. 17 where
modular multiplication is used for sharing a secret.)
• Instead of subtraction we use modular division.
• Instead of multiplication we use modular exponentiation.
• Instead of division we use the modular logarithm.
The resulting method is known as the ElGamal cryptosystem. Till now,
no one knows an algorithm to compute the modular logarithm (also known
as the discrete logarithm) for large numbers (numbers with more than 1000
digits) efficiently. All known algorithms, however, need several centuries even
when running on the fastest computers. Even if at some time in the future
the message is decoded without the private key, it does not help because the
party will be over by that time.

154 Dirk Bongartz and Walter Unger
Modular Multiplication and Modular Exponentiation
Before we describe how modular exponentiation can be performed efficiently,
let us take a quick look at modular multiplication first.
In our modular arithmetic, all calculations will use a prime number p,that
is, a number having exactly two distinct divisors, p and 1. As you know, the
first prime numbers are 2, 3, 5, 7, 11, 13, 17, 19,....
The prime number p is called the modulus for our calculations. The result
of the modular multiplication (a · b)modp is defined as the remainder of the
product a ·b when divided by p. For instance, (5 ·8) mod 17 = 6 since dividing
5 · 8 = 40 by 17 gives the quotient 2 (which we ignore) and the remainder 6.
Now we take a closer look at modular exponentiation. In a modular expo-
nentiation a number a is multiplied precisely b times by itself. Each time the
result of the multiplication is the remainder of the division by p. This result
is written as (a
b
)modp.
Theresultof(3
9
) mod 17 is 14, as shown in the following calculation.
Computing (3
9
)mod17
3
9
mod 17 = (3 · 3 · 3 · 3 · 3 · 3 · 3 · 3 · 3) mod 17
= ((3
8
mod 17) · 3) mod 17
3
8
mod 17 = ((3
4
mod 17) · (3
4
mod 17)) mod 17
3
4
mod 17 = ((3
2
mod 17) · (3
2
mod 17)) mod 17
3
2
mod 17 = (3 · 3) mod 17
=9
3
4
mod 17 = (9 · 9) mod 17
=13
3
9
mod 17 = (13 · 13 · 3) mod 17
=14
This example also shows that 3
9
mod 17 can be computed with fewer than
eight multiplications by cleverly using intermediate results in multiplications.
The following procedure uses this idea.
Computing (a
b
)modp
1Ifb = 0, then the result is 1.
2Ifb = 1, then the result is a.
3Ifb is odd, the result is ((a
b−1
mod p) · a)modp.
4 The only remaining case is that b is even and we compute:
5 h =(a
b/2
)modp.
6 The result is (h · h)modp.
In this description, for computing (a
b
)modp we used other values of the
form (c
d
)modp.Thevaluesc and d are always smaller than the values a

16 Public-Key Cryptography 155
and b. Therefore, this method works out and eventually terminates. From this
we get the following recursive algorithm:
Recursive algorithm for computing (a
b
)modp
1 ExpMod(a, b, p)
2 If b =0then return 1.
3 If b =1then return a.
4 If b is odd then
5 begin
6 h = ExpMod(a, b − 1,p)
7 return (h · a)modp
8 end
9 h = ExpMod(a, b/2,p)
10 return (h · h)modp
In the following table we present the values 2
b
mod 59 for all even b.This
table shows how irregular the results are compared to a normal multiplication
due to the application of the modulo operation in intermediate steps.
Values for 2
b
mod 59
b 2
b
mod 59
0 1
2
4
4
16
6
5
8
20
10
21
12
25
14
41
16
46
18
7
b
2
b
mod 59
20 28
22
53
24
35
26
22
28
29
30
57
32
51
34
27
36
49
38
19
b
2
b
mod 59
40 17
42
9
44
36
46
26
48
45
50
3
52
12
54
48
56
15
The modular logarithm problem is to do the inverse operation, which means
to obtain for a given number x (such as x =42)anumberb such that 2
b
= x.
Of course, for the modulus 59 this number b can be found by trying out
all possible exponents. But for large numbers this becomes very wasteful.
However, even for large numbers modular exponentiation is still possible, as
the numbers in the above algorithm quickly get smaller.
If the exponent b has ten digits, then at least a million possible solutions
have to be considered to find the modular logarithm. On the other hand, the
computation of the modular exponentiation with an exponent with ten digits
requires at most 65 modular multiplication. This shows the big difference
between the complexity of a modular logarithm and modular multiplication.
Nowadays, the method of ElGamal is used on numbers with more than the
thousand digits. Thus, the “complexity gap” becomes much larger: Trying out
156 Dirk Bongartz and Walter Unger
all possibilities is absolutely impossible, and in fact no alternative algorithm
is known that solves the discrete logarithm problem for moduli p as large as
this in reasonable time.
Description of ElGamal’s Cryptosystem
Now we are able to describe ElGamal’s cryptosystem. It is a simple transfor-
mation of the system which was presented above using limited mathematics.
In the above method the associative law (a · b) · c = a · (b · c) was used.
Within ElGamal’s cryptosystem a similar law for the exponential calculation
should apply. The notation g
x
indicates that g is to be multiplied with itself
x times. Without going into details, we just state the law which applies here:
(g
a·b
)
c
= g
(a·b)·c
= g
a·(b·c)
=(g
a
)
b·c
.
Furthermore, it is important that all numbers between 1 and p − 1 can
appear as values g
x
mod p, that is, for each number i between 1 and p−1there
has to be a number j with i = g
j
mod p. In such a case g is called a generator
(modulo p), as g generates all elements of {1,...,p− 1}. The following table
shows that 4 is not a generator modulo 7, but 3 and 5 are.
Generators for modulo 7: 3 and 5
i 3
i
mod 7
0 1
1
3
2
2
3
6
4
4
5
5
6
1
i
4
i
mod 7
0 1
1
4
2
2
3
1
4
4
5
2
6
1
i
5
i
mod 7
0 1
1
5
2
4
3
6
4
2
5
3
6
1
Alice – in the meantime she has moved on to high school – first finds a
prime number p and a generator g for modulo p. For example, let 59 be the
prime number and 2 be the generator. In the next step, Alice chooses her
private key x. With this private key she computes the first part of her public
key by y =(g
x
)modp, in our case, 42 = (2
x
) mod 59. She announces publicly
the numbers p = 59, g =2,andy = 42 on the bulletin board of her school.
Note that in the above table the number 42 does not appear. Thus the private
key of Alice is odd. Can you find her private key?
Numbers for Alice’s ElGamal system
59 prime number of Alice
2 generator of Alice
x private key of Alice
42 public key of Alice
16 Public-Key Cryptography 157
Bob wants to send the date of the new party to Alice. This year the party
is ten days later, so the secret number is 15. To send this secret, Bob reads
Alice’s three numbers from the bulletin board. Bob chooses 9 as the sending
secret. He computes: a =2
9
mod p, obtaining a = 40. To get the encrypted
message he further computes b = (15 ·42
9
) mod 59, which yields b = 38. Then
he announces these two numbers on the bulletin board of the school.
Bob’s ElGamal values
40 decryption help for Alice
38 encrypted message for Alice
Alice starts the decryption. At first she computes h =40
x
mod 59. The
result is 34. By “division modulo p,” Alice can find out that 33·34 mod 59 = 1;
we say that 34 is the inverse of 34 modulo 59.
Let us have a closer look at such inverses. When dealing with addition,
the inverse of a number x is −x since x +(−x) = 0. The inverse of x for a
multiplication is
1
x
because x ·
1
x
= 1. For modular multiplication the inverse
of a number x is a number y for which (x · y)modp =1.
Given a prime number p and an x between 1 and p − 1, it is possible to
calculate the inverse of x modulo p (it is unique) by fast exponentiation: Just
calculate y = x
p−2
mod p. Then, clearly x · y mod p = x
p−1
mod p, and it is
known (“Fermat’s Little Theorem” from Number Theory) that this number
is always equal to 1.
The message is decrypted by computing 38 ·33 mod 59. Alice thus obtains
15 – the original message.
In our description we avoided showing off the private key of Alice. You are
asked to detect this number. Maybe you see that this will be very hard if the
numbers become large.
Further Methods
There are many public-key cryptosystems that are built in a similar way. To
make them more secure, more complicated operations are used, for instance,
“elliptic curves” or even “hyperelliptic curves.”
Security
Of course, the question arises about how secure such a system is. One impor-
tant parameter is the size of the used numbers. The numbers have to be large;
so large that a program which uses trial and error takes a very long time. It
should take such a long time that the revelation of the secret is dispensable.
In our example it suffices to keep the secret safe till the party is over.
On the other hand, it could happen that suddenly one finds an algorithm
computing the modular logarithm efficiently. So far there exists no proof that

158 Dirk Bongartz and Walter Unger
such an efficient algorithm does not exist. Mathematicians and computer sci-
entists have been trying to find such a method for many years. Despite all
their efforts no such efficient algorithm has been found yet. Scientists there-
fore assume that such an algorithm does not exist.
If one day an efficient solution for the modular logarithm is found, then
the decryption by ElGamal will become insecure. We hope that this will not
happen. Note, however, that in this case we still could use the above trick
with other mathematical operations.
Further Reading
1. ElGamal’s cryptosystem is also described in Wikipedia:
http://en.wikipedia.org/wiki/ElGamal
cryptosystem
2. Chapter 14 (One-Way Functions)
In that chapter another public-key cryptosystem is mentioned, the so-
called RSA cryptosystem.
3. There are several books introducing encryption systems and discussing
their history. For instance, you may have a look at the following:
Simon Singh: The Code Book: Science of Secrecy from Ancient Egypt to
Quantum Cryptography. Anchor Books, 2000.

17
How to Share a Secret
Johannes Bl¨omer
Universit¨at Paderborn, Paderborn, Germany
The following story line appears again and again in movies and novels like
Cutthroat Island, TheGood,theBadandtheUglyand Treasure Island.Part
of a treasure map is found, but this part of the map is not sufficient to locate
the treasure. To find the treasure the whole map is needed. Therefore, the
finder of the fragment tries to find the other parts of the treasure map as well.
Of course, the owners of these other parts are also extremely interested in
finding the parts of the map they are missing, and so the adventure begins.
This story line is just one example of the problem we present in this
chapter: how to share a secret. We want to investigate how to partition a
treasure map or any other kind of information in such a way that, without
knowing all pieces, the treasure cannot be found or the information cannot
be reconstructed completely. We will see that there are much better methods
than just cutting the map into pieces. Actually, if we think about it, it is then
not very convincing that one needs all parts of a treasure map to find the
hidden treasure.
The general problem is easy to state. We want to partition a secret, let us
call it S, into a certain number of pieces or shares. The individual pieces are
then given to different persons. Furthermore, we want to achieve the following
goals:
1. If all persons collaborate and combine their shares, then they can recon-
struct the secret S completely.
2. However, if only a subset of the persons that received some piece of the
secret collaborate, then the persons in this subset should not be able to
reconstruct the secret S completely. Moreover, the persons in this subset
should only be able to gain little information about the secret S.
Of course, sharing a secret is not just a common story line in movies and
novels; it has many more serious and realistic applications. Imagine that an
important document of a government or an enterprise is stored in a safe.
There is consensus that the document will be published only if all members
of a special committee agree to the publication. To realize this, the safe is
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0
17,
c
Springer-Verlag Berlin Heidelberg 2011
