Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged
Подождите немного. Документ загружается.

170 Detlef Sieling
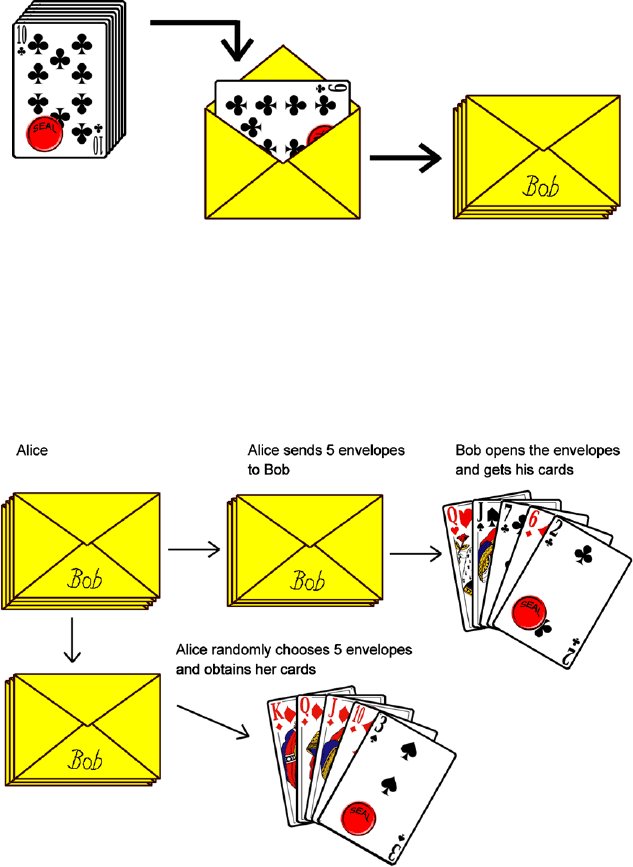
Later on, it will be crucial to prove who has put a card into a particular
envelope. Thus Bob signs each of the envelopes.
Then Bob shuffles the envelopes and sends them to Alice. Alice cannot
distinguish the envelopes according to their contents. Thus she is not able to
select good cards for herself and poor cards for Bob. So Alice can only shuffle
the envelopes again and select five ones for herself and five for Bob. This is
exactly a random selection of cards for herself and for Bob. Alice returns the
five envelopes to Bob. Then both players can open the envelopes and obtain
their cards.
How can the players cheat? For example Alice can open other envelopes in
order to get a larger number of cards from which she could select the best ones.
Obviously, Alice cannot be prevented from doing this. On the other hand, if
Alice does not cheat, she retains 42 closed envelopes with Bob’s signature,

18 Playing Poker by Email 171
and she can present those envelopes if the two players meet later on. Since
the envelopes are signed by Bob, Alice is not able to put a card back into
the envelope or into a new one. Bob could also try to cheat when he puts the
cards into the envelopes. For example, he could retain a card for himself and
leave an envelope empty. If he gets the empty envelope during the game, he
gets the card he retained and thus this is not at his advantage. Otherwise,
the empty envelope and Bob’s cheating will be detected at the latest when
Alice and Bob check the envelopes after the game.
How to Bid
The next step is the bidding. What is said during the bidding can also be
written into letters. Thus we do not need new ideas to do this by mail.
How to Replace Cards
After the bidding each player may replace one or more of his cards with
randomly chosen ones from the card deck. First Alice may replace n cards
(where n is between 1 and 5). Here we have the following problem: In the
first step Alice has to drop n cards, and only afterwards may she get the new
cards. If she takes her new cards by selecting envelopes as described above, it
is not possible to prevent her from opening the new envelopes and selecting
the cards to be dropped afterwards. Thus Bob also needs to be involved into
replacing the cards of Alice.
On the other hand, Alice cannot return the remaining 42 envelopes to
Bob because then she would lose the proof that she has not cheated so far.
Furthermore, Bob could have marked the yellow envelopes and could thus
recognize the envelopes with good or bad cards. He could do this, for example,
by signing the envelopes in a slightly different way. This can be done even less
obviously than shown in the following picture where the lower-case “b” in Bob
is written differently according to the contents of the envelope.
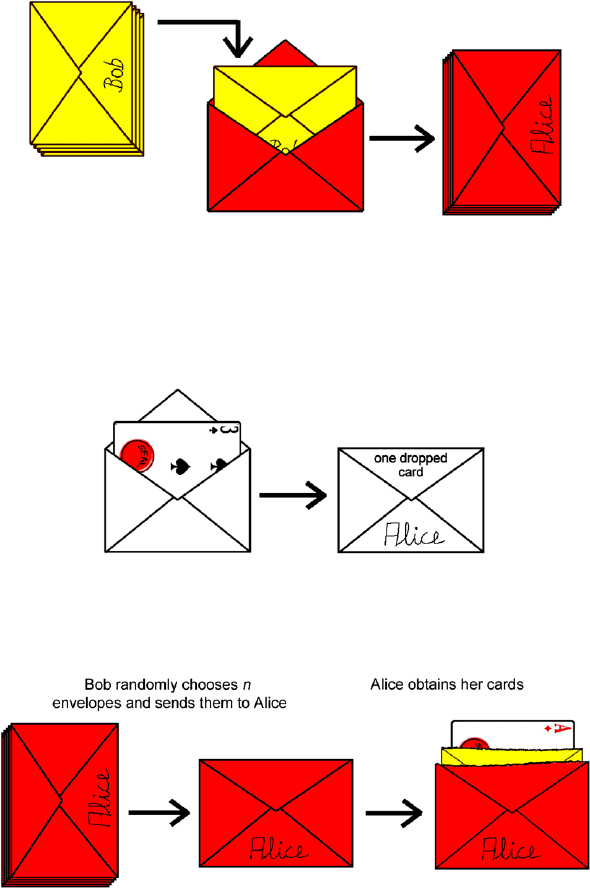
However, the trick with envelopes works again. Alice puts the remaining
42 yellow envelopes into slightly larger red envelopes, signs those envelopes,
shuffles them and sends the pile to Bob.
172 Detlef Sieling
Furthermore, she puts the n cards she would like to replace into a separate
envelope and sends it also to Bob. Bob must not open the envelope with the
dropped cards because he should not gain any knowledge on those cards.
Later on, both players together can verify that the envelope is still closed and
afterwards that it really contains n cards.
Since Bob cannot distinguish the red envelopes, he can only shuffle them
again and select n envelopes to return to Alice. In this way Alice gets the
replaced cards.
If Bob would like to replace cards, this can be done similarly, where Bob
has to put the red envelopes into another layer of envelopes.
The Showdown
The game ends with presenting the cards to the other player. Each player
writes a letter with the information on his cards. Each player retains his cards
18 Playing Poker by Email 173
in order to prove later on that he really has the cards he claimed. In this way
the winner is determined.
How to Verify That No One Has Cheated
For both players there are many possibilities to cheat by deviating from the
scheme described. For example, each player could open further envelopes in
order to obtain a larger choice for his cards or information on the hand of
the opponent. However, this is easily detected if the players meet after the
game. The players have to retain their cards and the closed envelopes until
this meeting. Then they can present the cards to their opponents and can
open the remaining envelopes together in order to verify that they did not
cheat.
Discussion
There are several obvious disadvantages in this poker scheme:
• Putting the cards into envelopes can only be done manually and it is
expensive. The envelopes cannot be reused.
• The check whether one of the players has cheated cannot be done before
the next meeting of the players. For each other game before this meeting
they need another card deck with a different seal.
• Snail mail is too slow to make the game interesting and it is more expensive
than email.
• If a letter is lost, the game cannot be completed. So, if a player recognizes
that he is likely to lose, he could destroy a letter because it is not possible
to find out who intercepted the letter.
Now the question arises whether there is some kind of “electronic” en-
velopes with similar or even better properties than paper envelopes. In par-
ticular, they could be produced using a computer and sent by email. This
saves the work of putting each card manually into an envelope. Furthermore,
emails can be stored by the sender and can be resent if they are lost.
Dealing Cards by Email
Electronic Envelopes
How can we realize envelopes with emails? The first idea is to use codes for
the cards. Bob creates and shuffles these codes and sends them to Alice. Since
Alice does not know of the correspondence between the codes and the cards,
she can select cards without knowing the cards. Before we describe how to
use the codes for shuffling and distributing the cards, we focus on the special
case that only Bob has to obtain cards. We sometimes assume that the cards

174 Detlef Sieling
have fixed numbers and that both players know this numbering scheme. We
assume that 0 corresponds to the ace of clubs, 1 to the two of clubs, 2 to the
three of clubs, ..., 12 to the king of clubs, 13 to the ace of spades, and so on
until 51 to the king of diamonds.
How to Shuffle the Cards and Distribute Them to Bob
At the beginning Bob randomly creates codes for the cards, i.e., a table like
the following one:
Card Code
0 (Ace of clubs) → 1
1(Twoofclubs) → 42
2 (Three of clubs) → 22
3 (Four of clubs) → 25
4 (Five of clubs) → 51
Card Code
5 (Six of clubs) → 0
6 (Seven of clubs) → 43
.
.
.
51 (King of diamonds) → 13
The left column of the table is a list of all cards. The right column has
been created randomly such that each number between 0 and 51 occurs exactly
once. Up to now Alice does not know this table.
In order to select five cards for Bob, Alice randomly chooses five codes
between 0 and 51 and send them to Bob. Then Bob uses the table in order
to find out his cards. If, for example, Alice has selected the codes 0, 1, 13, 42
and 51, according to the above table Bob gets the six of clubs, ace of clubs,
king of diamonds, two of clubs, and five of clubs. Since Alice does not know
the table, she cannot influence the choice of the cards for Bob. Furthermore,
Alice knows the codes already used such that she can avoid selecting some
card for a second time.
The method described is similar to that using the real envelopes. Instead
of putting the ace of clubs into a yellow envelope, Bob assigns a number to
it; in the example this is the number 1. If envelopes are used, Alice cannot
look into them. Here, Alice does not know the meaning of the code 1. In both
cases Alice cannot influence the cards selected for Bob.
However, at the end of the game, Bob could claim that he has created a
different table and in this way he could select better cards for himself. Thus
Bob has to fix a table in such a way that he cannot change the table later on.
We are going to show how this can be done using one-way functions.
One-Way Functions
One-way functions are presented in Chap. 14. We recall: A one-way function
f is a function that can easily be computed, but for which the inverse function
f
−1
is hard to compute. An example in Chap. 14 was a telephone directory.
Computing the one-way function f corresponds to finding the telephone num-
ber for a given name, which is obviously easy. Computing the inverse function
18 Playing Poker by Email 175
f
−1
corresponds to finding the name for a given telephone number, which is
obviously difficult.
How can we use one-way functions in order to prevent Bob from changing
the table with the codes of the cards? Similarly to the telephone directory, we
assume that Alice and Bob have copies of a book with a large number of tables
with codings. Furthermore, for each such table there is a unique number in
the book.
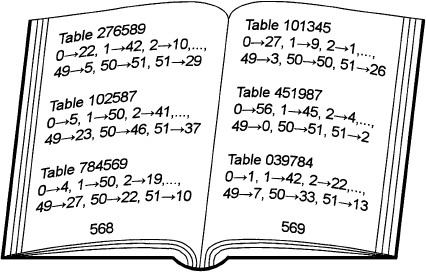
Then the distribution of cards to Bob can be done in the following way: In
the first step Bob randomly selects a table with codings from the book (e.g.,
the table in the bottom of page 569). Bob sends the number of this table to
Alice. In this example this is the number 039784. If Alice would like to find
the table used by Bob, she essentially has to scan the whole book. If this takes
too much time for her, she has no possibility to find the table with codes used
by Bob. Then her only possibility is to select five random number from 0 to
51 and to send them to Bob. Then Bob can obtain his cards according to the
table. The card with the number 0 (ace of clubs) has the code 1, the card
with the number 1 (two of clubs) has the code 42 and so on. At the end of the
game, Bob can send Alice the position of the table in the book. Then Alice
knows the table and can verify whether this table has really the number given
by Bob at the beginning of the game. Furthermore, she can verify whether
Bob really got the cards he claimed.
How to Replace Cards
Now replacing the cards does not require new ideas. If Bob would like to
replace the two of clubs in the previous example, he just says to Alice that
he would like to replace the card with the code 42. Since Alice does not know
that this code corresponds to the two of clubs, she does not know either which
card is dropped by Bob. Afterwards, Alice can select a new code in order to
send a new card to Bob. Since she knows which codes have already been used,
she can avoid distributing a card for a second time. We see that this is even
possible without Alice knowing the set of cards she has already distributed.
176 Detlef Sieling
A Mathematical Description
Now we describe the scheme from above a bit more mathematically. The book
with the coding tables corresponds to a one-way function f . This function
maps the positions of the coding tables in the book to numbers. In the scheme
from above, Bob randomly selects a coding table with the position x and sends
f(x) to Alice. Since f is a one-way function, it is hard for Alice to obtain x
from f(x). This corresponds to searching the whole book. At the end of the
game, she obtains x from Bob. Then Alice can easily compute f(x)andverify
that this is the number she got from Bob at the beginning of the game. Thus
Bob cannot cheat by the claim that he used some different coding table.
On the other hand, it is easy to store and search a whole book with a
computer. Instead of a book we should use one-way functions in order to
obtain a number from the coding table, and use this number to commit to
this coding table. However, here we would like to skip the details of such
one-way functions.
Each coding table can also be considered as a function. Above we already
mentioned the numbering scheme for the cards. Then the coding table is a
function b that maps the numbers of the cards (from 0 to 51) to their codes
(also a number between 0 and 51). The coding table also describes the inverse
function b
−1
which maps each code to the number of the corresponding card.
In order to compute b
−1
(z) we search for z in the right column of the table
and obtain the result in the left column. For tables with only 52 entries this
is easy to do. Since in the right column each number occurs exactly once, we
conclude that for all x we have b
−1
(b(x)) = x.
Distribution of Cards to Both Players
In order to distribute cards to both players, Alice and Bob use separate cod-
ing tables which they create independently and which the opponent does
not know. We call the function described by Alice’s coding table a and the
function of Bob’s coding table b. Another requirement on a and b is that
for all x between 0 and 51 it holds that a(b(x)) = b(a(x)). Mathematicians
call such functions commuting. For commuting functions a and b we obtain
the same result if we apply a on x and afterwards b on the result or vice
versa.
An example of commuting functions are the following ones:
a(x)=
x +25, if x +25< 52,
x +25− 52, if x +25≥ 52,
and
b(x)=
x +37, if x +37< 52,
x +37− 52, if x +37≥ 52.
18 Playing Poker by Email 177
In this example the coding tables are not given completely. Instead, we
give formulas how to compute the entry in the right column from the entry
in the left column. It is easy to verify that a(b(x)) and b(a(x)) coincide: For
the computation of a(b(x)) we first have to add 37 to x and afterwards 25,
where we have to subtract 52, if any of the results is larger than 51. For the
computation of b(a(x)) we just have to reverse the order of the additions.
Instead of 37 and 25 we could also use arbitrary different numbers.
This easy example of commuting functions is obviously not suitable for our
application of coding tables. If for example Bob obtains a(x) for the number
x, he can easily compute the number 25 which Alice uses for the addition.
In this way Bob obtains the whole function a and can break all the codes of
Alice. More details on commuting functions suitable for this application are
given in the articles mentioned in the section Further Reading.
Commitment to the Selected Coding Tables
Again we use a and b to denote the coding tables selected by Alice and Bob.
As above, we use a one-way function f. Alice computes f (a) and sends it to
Bob. Similarly, Bob computes f(b) and sends it to Alice. From f (a)andf (b),
Bob and Alice, resp., cannot obtain information on the coding table of the
opponent because f is a one-way function. On the other hand, the players have
committed to the selected coding tables a and b. After the end of the game,
Alice sends her table a to Bob. Then Bob can compute f (a) and verify that
a is really the table selected by Alice at the beginning of the game. Similarly
Alice obtains b from Bob and can verify that b is the table selected by Bob at
the beginning.
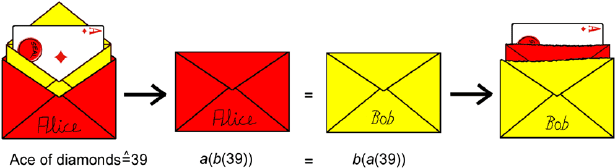
Putting Cards into Envelopes
If Alice wants to put the card x into an envelope, she only has to compute
a(x). In order to remove the card from the envelope a(x),
she applies the
inverse
function a
−1
to a(x) because a
−1
(a(x)) = x. Similarly, Bob can put
cards into envelopes using the function b. Since we used the numbers 0 to 51
for the cards and the codes (i.e. the envelopes) as well, Alice can also put
envelopes b(x) created by Bob into her envelopes by computing a(b(x)).
In our poker protocol for snail mail, in a first step Bob puts the cards
into envelopes and afterwards Alice puts those envelopes into another layer
of envelopes. Bob’s task corresponds to computing b(0),...,b(51). It is easy
to see that these are exactly the numbers between 0 and 51. Afterwards Alice
had to compute a(b(0)),...,a(b(51)). The result is again the set of numbers
between 0 and 51. Thus Alice and Bob know without any computation that
the set of codes a(b(0)),...,a(b(51)) is the set of the numbers between 0 and
51. Since Alice does not know b, she is not able to obtain a card from any
code. Similarly, Bob cannot do this because he does not know a.
178 Detlef Sieling
Distributing Cards to Alice
Bob selects from the list of unused codes (which consists at the beginning
of the number 0 to 51) an arbitrary code for each card that Alice has to
get and removes this code from the list. Since he does not know a,hehas
no influence on the selected card. On the selected code a(b(x)) he applies b
−1
and obtains b
−1
(a(b(x))) = b
−1
(b(a(x))) = a(x) because a and b commute and
b
−1
(b(z)) = z. Then Bob sends a(x)anda(b(x)) to Alice. Alice applies a
−1
to a(x) and obtains the corresponding card x. Furthermore, she can remove
a(b(x)) from the list of unused codes. Thus the same card is not distributed
again.
Distributing Cards to Bob
Alice selects from the list of unused codes one element for each card Bob
has to obtain. Since she does not know b, she cannot influence the selected
cards. On each code a(b(x)) chosen by Alice she applies a
−1
and obtains
a
−1
(a(b(x))) = b(x) because of a
−1
(a(z)) = z. Then she sends b(x)anda(b(x))
to Bob. From b(x) Bob computes x, i.e., the number of the selected card.
Furthermore, he can remove a(b(x)) from the list of unused codes.
Dropping Cards
In order to drop the card x without sending any information on x to the
opponent, the player sends a message with the code a(b(x)). We already know
that the opponent cannot obtain any information from a(b(x)).
Properties of the Electronic Envelopes
We compare paper envelopes with their electronic counterparts: First we look
at the selection of the cards for Alice. Putting the cards into yellow envelopes
by Bob corresponds to applying the function b. Putting those envelopes into
red envelopes by Alice corresponds to applying the function a. After selecting
the cards for Alice, in the electronic version of envelopes Bob can remove
the interior yellow envelopes by applying b
−1
without opening the outer red
envelopes and without getting any knowledge of the contents of the yellow
envelopes. Afterwards, Alice can open the red envelopes by applying a
−1
.Thus
the electronic envelopes have some properties that paper envelopes cannot
have:
• Alice cannot open the yellow envelopes, and Bob cannot open the red
ones. In particular, after the end of the game it is no longer necessary to
verify that the players did not open the unused envelopes because they
just cannot do this.
18 Playing Poker by Email 179
• It is possible to copy envelopes together with their contents and without
knowing the contents or obtaining any information about it.
• A red envelope with a yellow envelope and a particular card inside is
identical to a yellow envelope with a red envelope and the same card
inside. Thus it is possible to remove the interior yellow envelope without
destroying the outer red envelope.
How to Check Whether the Opponent Has Cheated
At the end of the game, the players send their coding tables a and b to their
opponent. Then they can compute f(a)andf(b), resp., and verify that a and
b are really the coding tables the other player has committed to. Using the
coding tables the players can verify all computations. During the game the
player have to cooperate to open a particular envelope because it is necessary
to evaluate a
−1
and b
−1
to open an envelope. Thus a meeting of the players
in order to examine the unused envelopes is no longer necessary.
Poker with More than Two Players
Up to now we only considered the situation of two players. What happens
for three or more players? Of course, we could try to generalize the above
ideas to a larger number of players. However, there is a fundamental problem.
Our starting-point was that the players cannot observe each other. How can
a third player prevent Alice and Bob from exchanging information about
their cards using their mobile phones? Commercial online poker systems have
the possibility to arrange groups of players that do not know of each other.
Another possibility would be the analysis of the behavior of the other players,
e.g., whether the player with the worse cards always refrains from bidding.
Nevertheless, it is hard to prove that the other players are cheating. So if we
would like to play with some larger number of players, we should meet, which
also might be more appealing.
Further Reading
1. Adi Shamir, Ronald L. Rivest and Leonard M. Adleman: Mental Poker.
In: The Mathematical Gardner, pp. 37–43. Edited by David A. Klarner,
