Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

390 Stefan N¨aher

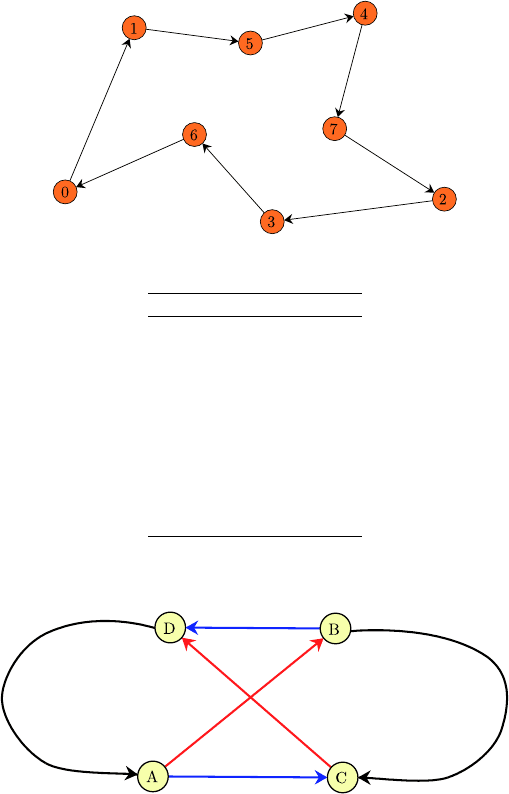
Fig. 40.5. The minimum spanning tour

Cities Running time

100 0.01 sec

200 0.08 sec

300 0.36 sec

400 1.30 sec

500 3.62 sec

600 8.27 sec

700 16.07 sec

800 29.35 sec

900 50.22 sec

1000 85.38 sec

Table 40.3. Running time of the MST-heuristics

Fig. 40.6. One step of the 2-OPT heuristics

and from D to A. Now check if these two parts can be combined to a shorter

tour by adding edges A −→ C and D −→ B.

Some Final Remarks

• There are many more heuristics for improving the quality of approximative

solutions. In many practical cases they are even able to ﬁnd the optimal

tour.

40 The Travelling Salesman Problem 391

• Algorithms for the exact solution of TSP have been considerably improved

over recent years. They can solve problems with several thousand cities in

a few hours.

• In the worst case solving TSP remains diﬃcult and requires an exponential

number of computation steps.

Further Reading

1. Wikipedia: Travelling Salesman Problem

http://en.wikipedia.org/wiki/Travelling

Salesman Problem.

2. An introduction by Martin Gr¨otschel and Manfred Padberg (in German)

http://elib.zib.de/pub/UserHome/Groetschel/Spektrum/index2.

html

3. The Travelling Salesman Problem Home Page

http://www.tsp.gatech.edu

4. The Knapsack Problem (Chap. 39)

An optimization problem with a similarly fast growing number of possi-

bilities.

5. Fast Sorting Algorithms (Chap. 3)

An introduction to recursive algorithms.

6. A demo program that provided the ﬁgures in this chapter

http://www-i1.informatik.rwth-aachen.de/

∼

algorithmus/

Algorithmen/algo40/tsp.exe

Simulated Annealing

Peter Rossmanith

RWTH Aachen, Aachen, Germany

Let us look at a simple combinatorial puzzle game: we can place several

quadratic tiles on a wooden board at 12 ×8 diﬀerent positions. At the begin-

ning the tiles might be placed as indicated in Fig. 41.1. As you can see, each

tile has four sides that may be colored blue, yellow, green, and orange.

We can exchange the positions of any two tiles, but we are not allowed to

rotate them. The goal of the game is to obtain as many neighboring sides of

tiles of the same color as possible: You score one point for each such neigh-

boring pair. In that way it is not possible to score more than 172 points: Each

Fig. 41.1. Background of the domino game: The pieces are arranged at random in

the box. Even in this situation we see 36 points

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

41,

 Springer-Verlag Berlin Heidelberg 2011

394 Peter Rossmanith

row contains 11 tile pairs and each column contains 7. There are 8 rows and

12 columns making altogether 11 · 8+7· 12 = 172.

Throughout this chapter we will continue to consider this tiling game as a

typical example that is similar to many problems in combinatorial optimiza-

tion. Some of the optimization problems mentioned in this book can be solved

quite eﬃciently (Chaps. 32, 33, 34,and35), while we can exactly solve others

only for relatively small input sizes (Chaps. 39 and 40). Here we are interested

more in the latter kind, in particular problems that can neither be solved by

trying out all possibilities nor with the help of backtracking. One method that

works well in many of those cases is simulated annealing, which is the topic

of this chapter.

What Is Simulated Annealing?

Simulated Annealing means simulating a process that involves ﬁrst heating

and then slowly cooling some material. There are several technological pro-

cesses based on a similar principle. For example, cooling red hot iron in met-

alworking quickly or slowly leads to materials with quite diﬀerent properties.

So why do that? Let us think about what happens to the particles (atoms) of

the metal:

The atoms are bound in a rigid crystal structure. When we start to heat

the metal they start to break free from their bonds and move about. If we

let the metal cool again, the particles will ﬁnd new bonds. Interestingly, often

their new distribution will be more regular than before. Doing it the right way

leads to metal that is softer, more ﬂexible, and contains fewer irregularities.

To better understand the eﬀects of slowly cooling, we can think of the

particles as small balls. If you just throw them into a vessel, they will lie

around higgledy-piggledy. What can we do to put them into order? Shake

them! At ﬁrst their disorder increases and the balls ﬂy about, but soon they

get into order all by themselves. If we, however, stop shaking too suddenly,

the balls will not be packed very closely.

This is also an important principle in the manufac-

turing of silicon semiconductors, of which computers’

processors and memory chips consist. In that case we

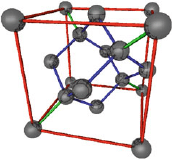
require very pure silicon crystals that do not contain

any defects. Usually silicon is polycrystalline: similarly

to grains of sand, many small monocrystals are placed

close to each other. Each monocrystal itself consists of

very many small elementary cubes that are ﬂawlessly

stacked next to each other. On the left side you can

see such a silicon elementary cube. On the outside eight silicon atoms form a

cube in whose interior ten more silicon atoms reside. In semiconductor pro-

duction we need relatively large monocrystals. To this end a monocrystalline

“pillar” is slowly drawn out of a bath of molten silicon. Consequently, with

41 Simulated Annealing 395

the help of a saw the monocrystal is cut into wafers, which ﬁnally are turned

into electronic semiconductors.

The monocrystalline state of silicon has the small-

est energy possible: the bonds between individual

atoms are strongest. From this perspective, the dif-

ference from our tiling game is not that big anymore.

Here, too, we are concerned with elementary par-

ticles whose relative position can be changed. The

bond between two neighboring tiles is stronger if

sides with the same color face each other. Again,

we are looking for a tessellation with smallest pos-

sible energy. If our game were a heated crystal, the

tiles would wildly jump about. The lower the tem-

perature gets, the harder it becomes to tear a tile

from its position, and the more stable bonds they

have with their neighbors, the stronger they stick to

their position.

It seems to be very hard to modify the board

game in order to make it behave just like that, al-

though it might be possible: Perhaps we could en-

force stronger bonds between sides of same color

by cleverly located magnets and mount the whole

board on a vibrating table. On the other hand, it

is much easier to simulate the whole process using a computer. Shaking the

board corresponds to swapping the positions of two tiles in the simulation.

Doing so, it is quite easy to compute how much the number of points scored

increases or decreases. At high temperatures we tolerate swaps that decrease

the number of points, while at low temperatures we get stricter and will tend

to allow only “good” changes to the board. The following algorithm can easily

be implemented in all usual programming languages:

Tiling Game

Repeat quite often:

1. Decrease the temperature a little

2. Swap two randomly chosen tiles

3. If the number of points has decreased:

• Randomly decide whether to keep this swap

• The probability for keeping the swap decreases with the temperature

• Undo the swap in case of a negative decision

This algorithm works surprisingly well for our tiling game. During the

execution of the algorithm the point score both increases and decreases. In

the beginning its ﬂuctuation is quite big, but the longer we wait – and the

lower the temperature gets – the smaller it becomes. Finally, we cannot notice

396 Peter Rossmanith

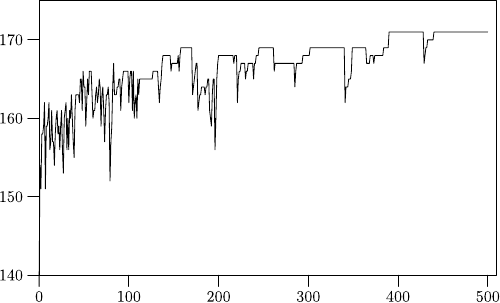
Fig. 41.2. How the point score changes by repeatedly swapping tiles: The y-axis

indicates the number of points and the x-axis shows the number of steps in units of

10,000. Altogether 500,000 steps are executed. In the end the score amounts to 171

points

any change in the point score anymore. Figure 41.2 shows how the point score

changes in the course of time, showing only scores higher than 140. This area

is reached very quickly, while further improvements become more infrequent

toward the end.

At this point, the question why we do not always take back swaps that

decrease the point score arises – in that way we would never voluntarily give

up earned points? Very often such a strategy works quite well and, therefore,

bears its own name: method of steepest descent (in our metaphor of reaching

the highest mountain, method of steepest ascent would make more sense, but

some optimization problems happen to be maximization problems, while oth-

ers are minimization problems, and the name was chosen based on the latter

ones). This strategy only climbs upwards, never downwards. If we want to

climb the highest mountain, we choose a direction that leads upwards, until

no such direction exists anymore, which is only the case on a summit. Can we

be sure that it is the highest summit? Not necessarily!

One who wants to climb the highest mountain, must be also willing to

descend along the way.

An application of the method of steepest descent to our tiling problem

leads to a solution with 167 points, from which point on it is impossible to

further increase the score by swapping tiles. This score is quite good. Simu-

lated annealing, however, leads to the better solution with 171 points, shown

in Fig. 41.3. Only one possible point is missing, whose location is not at all

easy to spot with just a quick glance on the board. (Hint: Tilt the picture by

◦

and look along the visually emerging diagonal lines.)

41 Simulated Annealing 397

Fig. 41.3. Positions of the tiles after application of simulated annealing: The score

is 171 points, and a closer look reveals that we got almost all possible points

Scoring 171 of theoretically possible 172 points is an excellent result

achieved by simulated annealing. We leave the natural question of whether a

perfect solution with 172 points exists as an open question to the interested

reader.

The Travelling Salesperson Problem

Let us have another look at a typical and famous problem in computer sci-

ence, the travelling salesperson problem, which is also a topic in Chap. 40

in this book: A salesperson likes to visit a number of cities, spending as lit-

tle time as possible for the trip. So the goal is to ﬁx the sequence in which

he or she visits the cities in such a way that the total mileage traveled be-

comes as small as possible. Surprisingly, this turns out to be a very hard

problem.

Maybe we can ﬁnd a nearly optimal solution by employing simulated an-

nealing. To ﬁnd some solution to start with is easy: Just put the cities in some

arbitrary order! So we start with a random tour and, of course, it is highly

improbable that this tour is short.

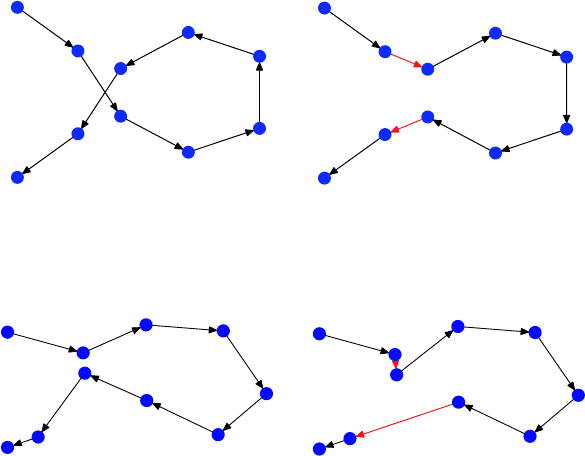
How can we improve this tour by incorporating only small adjustments?

Well, one possibility is to choose randomly a segment of the tour and traverse

it in the opposite direction:

398 Peter Rossmanith

Another possibility is to visit some city at a diﬀerent point in time, while

preserving the order in which we visit the remaining cities:

After adjustments of either kind, the new tour might be better or worse

than the old one. If the new one is better, we keep it, otherwise we return to

the old tour.

A big tour connecting 200 cities is depicted in Fig. 41.4. Of course, it was

found by using the two kinds of adjustments mentioned above and simulated

annealing.

Further Applications

We can employ simulated annealing if the following conditions are met:

1. The quality of a solution can be expressed as a number.

2. An initial solution can be easily computed.

3. There are simple adjustment rules that locally change a solution.

4. Every solution can be turned into every other solution by application of

these adjustment rules.

As these conditions are by no means very restrictive, it turns out that a

surprisingly large number of problems can be successfully solved by simulated

annealing.

Let us ﬁnally note that computer scientists were not the ﬁrst to use crys-

tal growing by slow cooling as a model for solving technical problems. If you

take this book into your hand, for example, you might notice the accurate

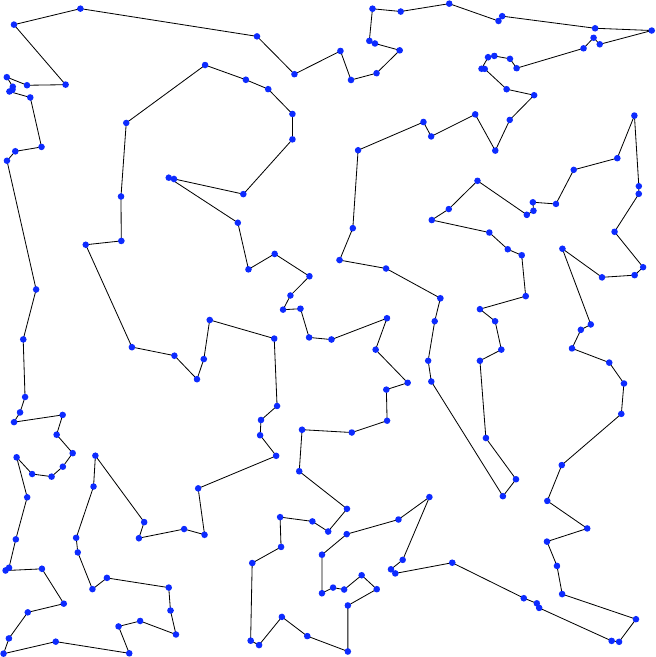
41 Simulated Annealing 399

Fig. 41.4. A tour that connects 200 cities

ﬁtting of the pages’ edges thanks to a precise cutting machine. If you, how-

ever, ﬂip quickly through the pages you might also notice that the edges of

the text are perfectly aligned. This alignment is due to the perfect adjust-

ment of the pages before binding them into a book. Technically, this is a

quite complex task: If you have a pile of loose pages (or cards from a deck),

it is quite hard to align their edges perfectly. Even brute force is not very

helpful.

The technical solution to this problem is a machine called a paper jog-

ger. It perfectly aligns the pages by using strong vibrations. Figure 41.5

shows a small paper jogger that can be operated manually and is used to

align exercise sheets coming freshly out of a printing machine. The control

dial is used to turn the vibration from strong to gentle: simulated anneal-

ing!