Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

350 Volker Claus, Volker Diekert and Holger Petersen

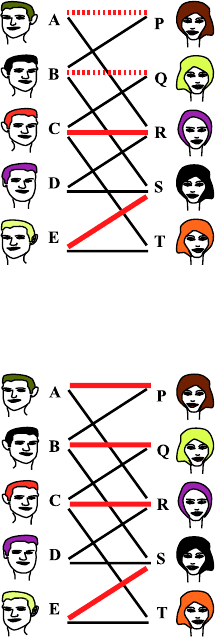
Fig. 35.6. The “experimental” repairing will be deﬁnitively adopted, and we get

the assignment {AP, BQ, CR, ES},whereBP has been replaced by AP and BQ

Fig. 35.7. Now we start the process again with the partnerless person D (note: D is

the name of the man in this example). Experimentally we match DR and herefore

remove CR. The newly partnerless person C may be matched to a pair with the

person T

totality of the possible female partners of these d + 1 men is exactly the set

of these d women. Consequently, one man has to remain partnerless. Thus we

can remove him from the beginning. This argumentation is explained again

in Sect. 35.6.

We maintain: If M is a maximum assignment, there is also a maximum

assignment M



, which has as many elements as M, but does not contain H.

Therefore one can abandon H. Therefore we delete H and start the algorithm

again with another partnerless person. (By the way, instead of H we could

have also deleted one of the last men from an experimental rearrangement.

This is rarely done in practice. First the important persons from the broker’s

point of view receive a partner. The approach described here guarantees that

once-arranged persons are not partnerless in the end.)

35 Marriage Broker 351

Fig. 35.8. Finally we have obtained the set M = {AP,BQ,CT,DR,ES}.Now,

every person has a partner and therefore the algorithm ends. (The experimental

rearranging takes up as many steps as there are edges left, because already tested

persons will not be tested again)

(d) The procedure ends when every person not deleted has a partner, that

means it is included in the set M .NowthissetM is the maximum assignment.

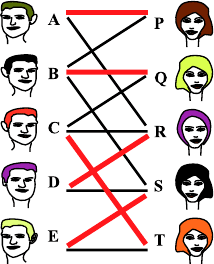
So how is the gradual increase of the number of couples in the assignment

set M (see Figs. 35.4—35.8)? The red edges belong to the couples of the

set M. The black edges show the remaining friendly relations (L−M). Now

the set M is reordered every time. We look at a path of alternating black and

red edges, starting and ending with a black edge and which has a partnerless

person at the beginning and at the end. If this happens, we can replace in M

the red edges by the black edges of exactly this path. In this way the number

of couples is increased by 1.

Hint: Such paths of alternating black and red edges, whose ending nodes

do not have outgoing red edges, are called augmenting paths.

35.4 The Algorithm

The following Marriage Broker algorithm provides a maximum set M of

couples, if the sets H, D,andL are given. It is clear that one just has to

look at one of the two sets H and D in order to choose the next partnerless

candidate. We restrict ourselves to the set H (see line 2 of the algorithm); in

practice one takes the smaller of the two sets H and D.

Given: The sets H and D, and the set L as the set consisting of only one

couple HD for some H from H and D from D.

352 Volker Claus, Volker Diekert and Holger Petersen

The algorithm Marriage Broker calculates a maximum set of couples M

1 choose a couple HD from L; M := {HD};

2 while there is still a partnerless person H in H do

3 follow all paths starting from H, which consist alternately

4 of one edge from L, which is not in M,

5 and one edge from M and

6 contains no person more than once;

7 if one ﬁnds a partnerless person

8 (which necessarily is in D)

9 then replace all edges in M on this path in M

10 by edges which are not in M on this path;

11 else (in this case there is no such path)

12 remove H from H

13 end if

14 end while;

15 return M;

Inside the while-loop one has to realize a systematic search in the part

“follow all paths starting from H,....”Thispartisimplemented“recursively.”

We have already written in Sect. 35.3, part (b): “Now one tries to take away

woman D from man H



...”. This is exactly the recursion that has to do the

same procedure with H



instead of H,ifH



hasn’t been treated already. One

should maintain in a boolean array the components which are set to false at

the beginning of the while loop (before row 3 in the program) and in which

one records if a person has been considered in this iteration or not. How the

overall procedure is implemented can be found in books. (At the end of this

chapter is a list of references.)

35.5 The Marriage Theorem

That the procedure works correctly is based on the Marriage Theorem of the

English mathematician Philip Hall in 1935. It follows from this theorem that

there exists an assignment of all men to appropriate women if and only if the

following marriage condition holds: For each subset of men, there is an at least

equally large subset of potential female partners.

The condition means that if, e.g., we look at 17 men from the set H,then

there are at least 17 potential female partners available for them. Instead of

17 we may also use any other number. Initially just the right relation of the

numbers is important. The assignment is insigniﬁcant at this time.

The criterion of the Marriage Theorem is not directly suitable for ﬁnding

a solution. First, an inspection for each 50 men and women would need more

than one million years, even if one billion combinations of men per second

could be examined (because you have to test 2

=1,125,899,906,842,624

subsets). Second, the theorem only provides information whether a solution

35 Marriage Broker 353

exists, but not what it looks like. For this we need the algorithm described

above.

35.6 Where Is the Marriage Theorem Needed by the

Algorithm

The Marriage Theorem is needed by the algorithm at the point where one

has to ﬁnd at least another man whose partner gets newly assigned and who

has the chance to ﬁnd a diﬀerent woman for himself. We explain this with the

help of an example:

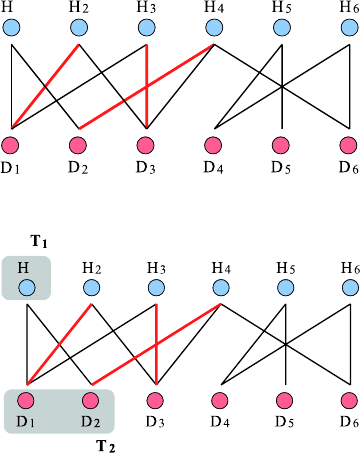
Consider Fig. 35.9.LetM = {H

}. H is partnerless. We

start with H.

{H} is a subset T

. To proceed, the subset {D

} = T

(= all with H

connected persons) belonging to T

has to be at least as large as |T

| =1

(Marriage Theorem!). See Fig. 35.10.

Now we replace H

on a trial basis by HD

,makingH

partnerless. We

could also replace H

by HD

,makingH

partnerless. Overall, we have

to ﬁnd partners for T

= {H, H

}. The set of women belonging to T

= {D

}, see Fig. 35.11. Again | T

|≤|T

| holds, so following

the Marriage Theorem there has to exist an assignment here. We detect this

by further examining the men belonging to women from T

, etc.

Fig. 35.9. M = {H

}, H is partnerless

Fig. 35.10. |{H}| ≤ |{D

354 Volker Claus, Volker Diekert and Holger Petersen

Fig. 35.11. |{H, H

}| ≤ |{D

If a solution exists, the Marriage Theorem ensures that the algorithm can

always proceed at any point with a person who has not yet been considered.

35.7 Time Analysis

The running-time of the procedure can be estimated easily from above. We

assume that there are n men and n women as well as m edges (= number

of elements in the set L). The while-loop in the algorithm is ﬁnished after

at most m steps, because each person is taken into account not more than

once and therefore each edge has to be examined only once. Because after

every loop either one man is eliminated or another couple is added, the whole

process ends after the while-loop has been executed (n − 1) times. For the

duration estimation we receive n · m as upper bound for the number of steps

taken by the execution of the algorithm.

Are there faster ways to calculate a maximum set of couples? One piece

of evidence of wasted time in our algorithm is that at the beginning of a

pass of the loop no information is available, although earlier passes had col-

lected information about the course of augmenting paths. Making clever use

of this, one can achieve a running-time proportional to m ·

√

n,savingthe

factor

√

n. This accelerated procedure was developed in 1971 by the Ameri-

can researchers John E. Hopcroft and Richard M. Karp. For these and many

other achievements these two researchers received the Turing Award in 1986

and 1985, respectively. [This is a kind of Nobel Prize in Computer Science.]

Further Reading

1. In Chap. 34 of this book the problem of a maximum ﬂow is examined.

A solution of this problem can be used to determine a maximum set

of couples. Furthermore, the procedure that was presented here can be

generalized to arbitrary graphs. (Think for yourself or refer to one of the

following books.)

35 Marriage Broker 355

2. Thomas Ottmann, Peter Widmayer: Algorithmen und Datenstrukturen.

Spektrum Akademischer Verlag, 2002. A standard textbook written in

German. In the chapter Zuordnungsprobleme maximum assignments are

found with the help of the calculation of maximum ﬂows.

3. Reinhard Diestel: Graph Theory, 3rd edition. Springer, 2006. Chapter 1

deals in great detail with pairings in general and bipartite graphs. There

you can also ﬁnd a proof of the Marriage Theorem.

4. Dexter C. Kozen: The Design and Analysis of Algorithms. Springer, 1992.

This book contains 40 chapters on topics of the theory of algorithms, each

of which corresponds to a lecture. In Chaps. 19 and 20 the more eﬃcient

method of Hopcroft and Karp with the corresponding correctness proofs

is presented.

5. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Cliﬀord Stein:

Introduction to Algorithms. MIT Press and McGraw-Hill, 2001. Section

26.3: Maximum bipartite matching, pp. 664–669. This is a very detailed

and very successful book on the theory of algorithms.

6. Several articles about the Matching Problem and the Marriage Theorem

can be found in the free encyclopedia wikipedia, www.wikipedia.org.

Acknowledgements

We thank Botond Draskoczy and Sascha Riexinger for technical support.

The Smallest Enclosing Circle –

A Contribution to Democracy from

Switzerland?

Emo Welzl

ETH Z¨urich, Z¨urich, Switzerland

The ﬁre service needs a new station and it should be located optimally with

respect to the houses served by it. The quality of the location is measured by

the maximum of the distances to the relevant houses, and this greatest dis-

tance should obviously be as short as possible. We idealize the houses and the

new location as points in the plane and model the real distances by distances

between the points. So the input for our problem is a set P of points in the

plane.

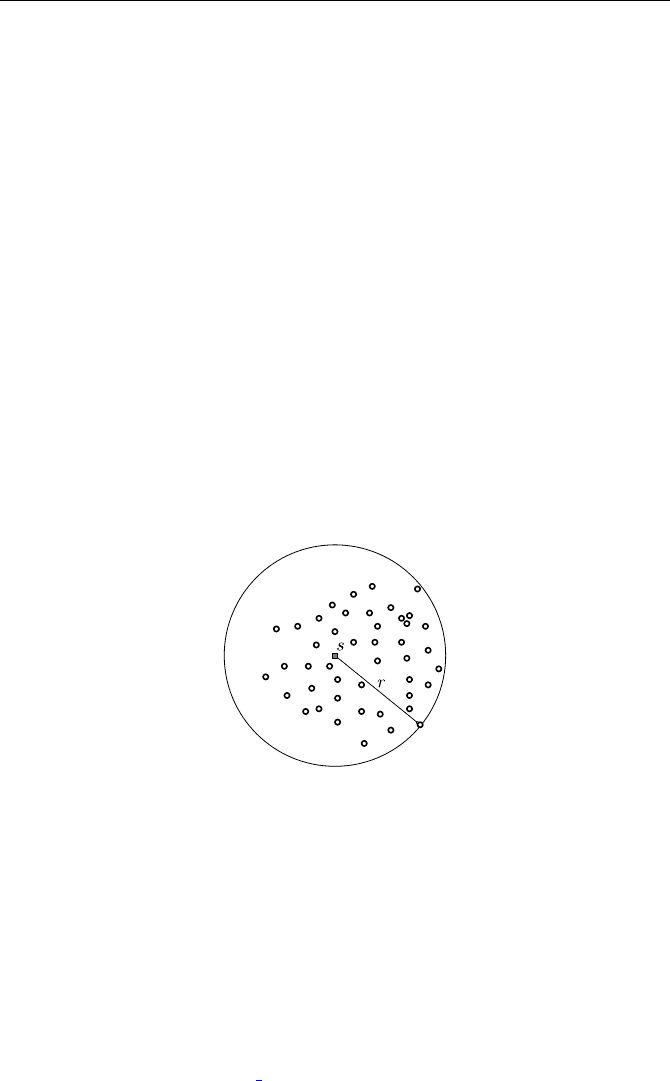
Letuschooseapoints as a potential location. The distance from s to the

farthest point in P will be denoted by r. Then a circle of radius r centered at

s encloses all the points of P .

It is clear that the best location is the center of a circle enclosing all the

points of P that has the smallest radius. (From there, the ﬁremen can reach

even the farthest house as fast as possible.) Such a circle exists and is unique

– we take this as a fact.

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

36,

 Springer-Verlag Berlin Heidelberg 2011

358 Emo Welzl

There are many houses and people are thinking how to decide on the best

location.

Somebody got the idea to invite representatives of a small random sample

of, say, 13 houses and to let them determine the best location for them-

selves – without any regard for the other houses. A method can be found

in the literature, which indeed solves the problem quickly for 13 houses, but

unfortunately turns out to be too slow for all the houses.

So they come up with a proposal for a place s

and a radius r

,sothat

the circle with the center s

and radius r

encloses all the chosen houses – it

is the smallest enclosing circle of R

The ﬁrst location is found.

Even though the set R

is chosen at random, people strongly oppose this

choice of location, especially the occupants of the houses standing outside the

determined circle.

To accede to the protests, a second sortition is called, but, as before,

nobody knows how to ﬁnd the smallest enclosing circle for such a large set

– it was already hard enough for 13. The proposal to invite all who stay

outside the ﬁrst circle appears unrealistic, too. It comes down to the following

compromise: all houses standing outside the ominous circle have two entries

in the sortition of 13 new representatives.

36 The Smallest Enclosing Circle 359

The 13 representatives, a set R

, are chosen, and they meet and agree

on their most preferred location s

and the corresponding radius r

of the

smallest circle enclosing R

Less surprisingly, even this encounters resistance. Again, there are many

houses standing outside the circle determined as a solution for R

Now, we should take into account that the municipality has not yet secured

the sources for ﬁnancing of the new ﬁre-service building. Therefore they like

the decision-making process – they are actually glad when this procedure does

not lead quickly, if at all, to a conclusion satisfactory for everyone.

So the result of the second round is rejected as well. For the next round,

the number of entries is doubled for every house standing outside the second

circle. If there is a house out of the circle for both the solutions determined

so far, then it gets in return four tickets in the polling urn!

Round three proceeds as before.

Et cetera, et cetera.

It becomes a routine. The circle-ﬁnding emerges as a popular entertain-

ment, not least because the municipality provides food and drinks. It is no

longer disappointing to be out of the announced circle, as the proposal would

not be realized anyway and the chance of participating in the next meet-

ing grows. The polling urn swells up, but the municipal secretary has soon

arranged for an electronic sortition (encouraged by Chap. 25 on random num-

bers).

But then, after 13 representatives have met again and proposed a solution,

which is the best for themselves, and themselves only, something unexpected

happens. No house is outside the calculated circle. The information spreads

quickly and a speedily obtained expertise conﬁrms what all have guessed: This

must be the smallest circle enclosing all points. A circle enclosing all points

cannot be smaller than a circle enclosing only 13 points after all.

The optimum location is found!

Have we been lucky that the chosen representatives were so successful, or

should we have been expecting it? The latter: We have learned a randomized

(i.e., based on randomness) algorithm developed by Kenneth Clarkson. It

calculates the smallest enclosing circle for n points. It can be shown that the

procedure computes the circle with probability 1 and the expected number of

rounds is in fact only logarithmic in n. It is necessary not to set the sizes of the

randomly chosen subsets too small (in our story 13) – though 13 is enough,

independent of how big n is. In the same way, it is also possible to calculate

the smallest enclosing ball of points in 3-dimensional space or even in higher

dimensions (only the random sample must be somewhat bigger depending on

the dimension).