Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged
Подождите немного. Документ загружается.


15
The One-Time Pad Algorithm – The Simplest
and Most Secure Way to Keep Secrets
Till Tantau
Universit¨at zu L¨ubeck, L¨ubeck, Germany
School started just a few weeks ago and Max is already dreading the upcoming
exam in computer science, which will be about something with the slightly
menacing name “encryption algorithms.” Max’s dread is not unfounded since
he has almost no clue as to what “encryption algorithms” might be about,
which in turn is due to the fact that all of Max’s attention has lately been
focused on Lisa, his new girlfriend. Lisa, by comparison, is not only fascinated
by Max, but also by cryptology. Since Max simply has to pass the exam, Lisa
devises a rather straightforward plan: “Fortunately, the exam will consist only
of multiple choice questions, so all I need to do is to pass to you slips of paper
on which I will write the answers to the questions. The teacher never notices
such things.” Max raises a slight objection: “But Peter will be sitting between
us.” Lisa answers: “Ah, don’t worry about Peter, I can sweet-talk him into
passing on anything I give him. So, on the paper, I will put a 1 for each answer
box that you should check and I will put a 0 for the other answer boxes. For
instance, if there are five answer boxes and you should check the first and the
third, I will send:
Lisa’s plan works remarkably well: Lisa and Max (and also Peter by the
way) get excellent grades. However, the teacher becomes somewhat suspicious
since Max is not renowned for his great knowledge concerning the subject. She
decides that during the next exam Max’s former girlfriend, rather than Peter,
will sit between Lisa and Max. The teacher’s idea seems to go in the right
direction since Max starts brooding: “I’d rather fail the exam than have her
copy the answers!” (Max obviously is not all that fond of his former girlfriend.)
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0
15,
c
Springer-Verlag Berlin Heidelberg 2011

142 Till Tantau
Lisa gives the matter some thought and then informs Max: “Ok, it seems
like we will have to encrypt the solutions using a one-time pad.”
“One-time pad?” Max asks, looking slightly clueless.
“That’s an encryption method for securely encrypting messages a single
time.”
“Encryption method?” Max asks, looking even more clueless.
“You really don’t pay attention in class ...” Lisa begins. Max interrupts
her by interjecting “But I love you!”, which Lisa ignores and continues: “En-
cryption means that you and I agree on a key beforehand. I can use this key
to lock the answers to the exercises. You can then use the key to unlock the
answers once more. Your former girlfriend won’t be able to find out the correct
solutions without the key.”
“Eh?” is Max’s only answer, being totally lost at this point.
Encrypting Messages
“Pass me five coins from your wallet,” Lisa asks. Max obliges, although he
seems to mumble something along the lines of “But I will get them back ...”
Lisa places the coins on the table and continues: “When a coin face displays
a number, you must check the corresponding box, otherwise you don’t. For
instance, if the first and third box should be checked, we can represent this
using coins as follows:”
“Very well. Whatever. I don’t really see where you are going with this,”
Max answers, slightly bored. “It does not matter whether you write 10100 on
a piece of paper or use five coins, my ex-girlfriend is not that stupid. She will
catch on that this means: Check the first and third boxes.”
“Ah, but now encryption comes into play. Pass me that deck of notes,
thanks. On some of them I’m going to write ‘flip’ and on some others I’m
going to write ‘do not flip’. Now you pick five of them randomly and place
them below the coins.”
MaxdoesasLisaasks:

15 The One-Time Pad Algorithm 143
“Great,” Lisa says encouragingly. “Those notes will be our key, which we
fix before the exam and have to learn by heart.”
“Now I do see where you are going with this.” Max replies, not being
stupid after all. “Instead of the original coins you pass the coins after they
have been flipped or not flipped according to our key:
My ex-girlfriend can look at this as long as she wants, it won’t help her
one bit – for instance, the first coin can both mean ‘check’ or ‘do not check’
the first box. The chances are exactly fifty–fifty.
However, come to think of it, why should she pass notes at all? Why
shouldn’t she just swallow them to spite me?”
“She also wants you to pass the exam – so that she can pester you next
year in class.”
“Arghh,” Max cringes, then gives a big sigh. “Well, let’s go over the plan
once more: In the exam you solve the first question. Suppose you want to tell
me that I should check the first and third box, which corresponds to 10100.
However, since our key says that the first and fourth ‘coin’ should be flipped,
you send the following instead:
“I have memorized the key and can ‘flip the coins’ once more, which yields
10100. Thus, I check the first and third box.”
“I knew my boyfriend was reasonably smart.” Max looks suspiciously at
Lisa, but she continues: “You will have to agree that this one-time pad method
is pretty simple, but still perfectly safe. By the way, we are not the only ones
who use this method: When heads of state want to send each other messages
and they really want to make sure that these messages are kept secret, they
also use a one-time pad.”
Max bursts out laughing. “You really believe that when the American
president wishes to send a message to the German chancellor, he is going to
start flipping coins and write zeros and ones on a postcard?!”
“Obviously not,” Lisa replies grumpily, “a computer will do that for them.
For this, one needs to write down the algorithm, which would be a rather
good exercise for you.”

144 Till Tantau
The Algorithm
“Let’s see,” Max starts, still smirking. “First of all, I think that, indeed, there
really is only one algorithm because both ‘encoding’ or ‘locking’ our messages
and ‘decoding’ or ‘unlocking’ them work in the same way: In both cases we
start with an array of zeros and ones and a key, and in both cases we end up
with an array of zeros and ones once more. All the algorithm needs to do is
to replace zeros by ones and vice versa, whenever the key says ‘flip’.”
The algorithm OneTimePad encrypts and decrypts the array A with n
entries using the key.
1 procedure OneTimePad (A, key)
2 begin
3 for i := 1 to n do
4 if key[i] = “flip” then
5 if A[i]=0then
6 A[i]:=1
7 else
8 A[i]:=0
9 endfor
10 end
“Exactly” Lisa replies. “That’s one way to do this. However, the key nor-
mally is not an array of strings like ‘turn’ or ‘do not turn’, but rather also
an array of zeros and ones. A one in the key array means ‘turn’, while a zero
means ‘do not turn’. The algorithm can then be rewritten rather succinctly
as follows:”
Short version of OneTimePad.
1 procedure OneTimePad (A, key)
2 begin
3 for i := 1 to n do
4 A[i]:=A[i] xor key[i]
5 endfor
6 end
“Ah, just a moment,” Max interrupts. “I think I remember, rather vaguely
I might add, that ‘xor’ stands for ‘eXclusive OR’. But I can’t really recall what
that is supposed to mean.”
“The ‘exclusive or’ tests whether exactly one of two numbers is a 1. If
this is the case, the answer is 1, otherwise 0. So, in order for the exclusive
or to be 1, either A[i]mustbe1orkey[i] must be 1, but not both. These
two conditions exclude each other, hence the name. Have a look at this table,
which shows what’s going on.”
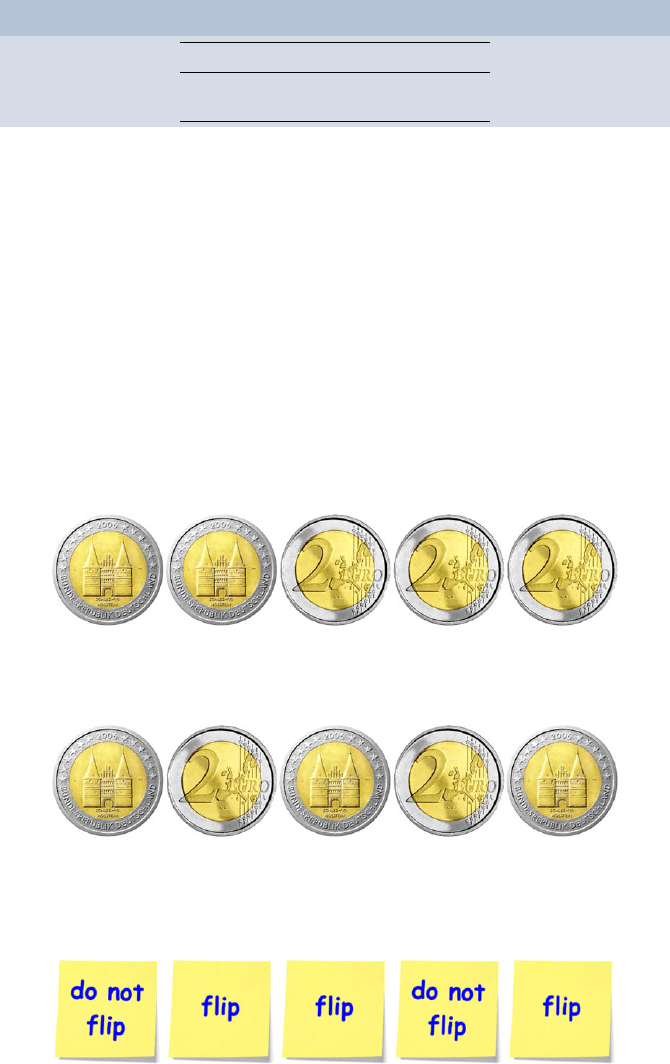
15 The One-Time Pad Algorithm 145
Table showing the values of A[i]xorkey[i].
key[i]=0 key[i]=1
A[i]=0 0 1
A[i]=1 1 0
“I see. This ‘xor’ is exactly what we need since it is going to ‘flip’ the value
of A[i]whenkey[i] = 1, and it’s going to leave A[i]asitiswhenkey[i]=0.”
Breaking the Code
Max is rather pleased with the algorithm. “I like this method. All I need to
do is to memorize a key consisting of five little notes and we can then use it
for the whole exam. That’s much easier than actually studying cryptology.”
“Unfortunately, my sweet Max, things aren’t that simple. Suppose we are
going to use the same key for all of the twenty questions of the exam, each
having five check boxes. Suppose your former girlfriend succeeds in solving
just one question by herself and gets my encoded message. For instance, I find
out that the last three boxes must be checked for this question. Using coins,
this would be represented like this:
“This will also be known to her if she can answer the question by herself.
Now she gets a note from me with the encoded messages 01010 or, written in
coins:
“I think you can see the problem?”
“Indeed, she can deduce the key! Obviously, the first coin has not been
flipped, while the second has been, and so on. She will know that our key
must be:
146 Till Tantau
“Once she has got the key, she can solve all the other questions! That’s a
disaster!”
“That’s why the method is called one-time pad method. The key can only
be used once. If you do not follow this rule, it is pretty easy to find out
the key that has been used. One of the older methods for encrypting wireless
communication used the same key over and over again – and so the keys could
be deduced pretty quickly. So, if you were using a laptop in a coffeehouse to
write emails, students sitting at the other tables could easily read all the emails
you send me.” At this point, Max’s facial color undergoes a rapid succession of
changes. First, his face is completely drained of all color, only to turn bright
red seconds later. Lisa gives him a sweet smile: “Those highly paid people
who came up with the method obviously did not pay attention in school. We
will have to memorize a new key for each question.”
“But that’s horrible, I’ll have to memorize the correct sequence of 100
times ‘flip’ or ‘do not flip’. It would be much easier to just study the material
on cryptology instead!”
“Hmm. Perhaps that’s the best solution anyway. Cryptology is not that
difficult, after all.”
Further Reading
1. Chapter 16 (Public-Key Cryptography)
The method presented in this chapter allows one to reuse keys, unlike the
one-time pad. Even more impressive is the fact that the keys can even be
made public!
2. Chapter 17 (How to Share a Secret)
Some secrets, like the keys in cryptology or the position of a pirate’s chest
on an island, are too important to just store them in one place. This
chapter describes a method for splitting up a secret into parts so that you
really need to get together all parts in order to retrieve the secret.
3. Chapter 25 (Random Numbers)
Lisa and Max created their key by randomly drawing notes from a deck.
However, how does a computer generate random keys? This is a surpris-
ingly difficult question since, normally, there is nothing random about the
way a computer works.
4. http://en.wikipedia.org/wiki/Cryptography
This star-reviewed Wikipedia article is a nice introduction to cryptology
in general.
5. http://en.wikipedia.org/wiki/One-Time-Pad
This Wikipedia article describes the one-time pad algorithm and some
variants in more detail. It includes some background on the history of the
algorithm.

16
Public-Key Cryptography
Dirk Bongartz and Walter Unger
Gymnasium St. Wolfhelm, Schwalmtal, Germany
RWTH Aachen University, Aachen, Germany
Who has never thought about sending a secret message? Even Julius Caesar
did so. He allegedly moved each single character in his message three posi-
tions to the right within the alphabet. Using this procedure, A becomes a D,
B becomes an E, and so on. Finally, W is replaced by Z, X by A, Y by B, and
ZbyC.
If one knows this procedure it is certainly quite easy to decrypt an inter-
cepted “secret message.” For instance, what is behind the following message?
To make this idea a little bit more general, one obviously can choose a
number k (k<26) and move each character of the message to be encrypted
(usually called plaintext) k positions to the right. In this way we obtain a
secret message, the so-called ciphertext.Theencryption method is moving the
characters to the right within the alphabet, starting again from the beginning
when the end is reached. In this context k is called the (secret) key.Tode-
crypt the message, one simply has to move each character in the ciphertext k
positions to the left.
Once anybody knows the key in such a system, he is able to encrypt as well
as to decrypt all messages. For this reason these procedures are called sym-
metric cryptosystems. Also, the one-time pad method, presented in Chap. 15,
belongs to this category.
Summing up, this means that everybody who could encrypt a message
could also decrypt it and other messages encrypted by the same method.
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0
16,
c
Springer-Verlag Berlin Heidelberg 2011
148 Dirk Bongartz and Walter Unger
On the other hand, there is the major drawback that the regular receiver
of the ciphertext must know not only the used method but also the used key.
But how do we exchange this key if communication partners are really far
away from each other?
In the next section we show that having the same key for encryption and
decryption is not essential. It is even advantageous if keys are not equivalent.
Methods based on two kinds of keys, where one is public and the other one is
private, are called asymmetric cryptosystems.
Public Keys
At first sight, this title might look senseless and the question might come up
how this could work out. For any symmetric system a publicly known key
would reveal all secrets. The problem for the symmetric systems is that it is
possible to compute the decryption key from the encryption key.
However, looking at it again we see that we may use a public key for
encryption, and keep a (different) key for decryption secret. We only have
to make sure that the decryption key cannot be computed from the public
encryption key.
Such a system would be attractive because anyone could send a secret
message to you and only you would be able to decrypt the message.
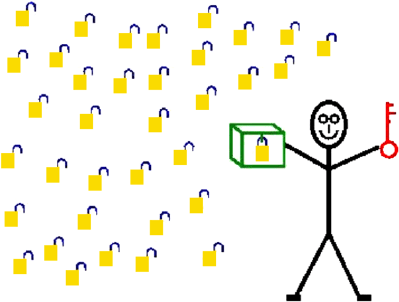
In fact, it is not so complicated to construct such a system. Just assume
you have several thousand padlocks which may be opened by a single key.
(Note that this is an unusual requirement, as normally only single padlocks
with several keys are on offer.) Now, you distribute your padlocks to all your
friends. You may even place a pile of padlocks at the school office or library.
The key to open all these padlocks stays in your possession.
Now, anyone who wants to send a message to you may take a box and
place the message in it. Because you need no key to lock one of the padlocks,
16 Public-Key Cryptography 149
everyone is able to lock away a message in a box. Furthermore, only you are
able to read the messages because you hold the only key opening the boxes.
Thus, your friends may even ask the biggest blabbermouth of the school to
forward the box to you.
This example shows that such a system is possible. However, there is one
drawback. This example requires a big effort. We have to purchase these pad-
locks and we have to distribute them. This would be quite expensive and
labor-intensive.
It would be nice to have a system which provides such a public-key system
without padlocks. This is possible in principle, using the one-way functions
from Chap. 14. Loosely speaking, it is easy to compute the one-way function
in the forward, standard direction, but hard to do the reverse: given a function
value, recover the corresponding argument.
In our case we need some system in which encryption is easy (so that
everyone is able to send us a message) but decryption is hard. However, you
as the legal receiver should be able to decrypt easily. You should keep some
backdoor for this. One possibility would be to use the inverse telephone book
from Chap. 14. However, here we describe a different idea.
A Limited Algebra
Real public-key cryptosystems which employ computers to encrypt and de-
crypt messages use advanced algebra. We do not describe this kind of arith-
metic here. Instead, we illustrate the principles by using a limited algebra.
Within this limited algebra we only use addition, subtraction, and multi-
plication of integers. We explicitly assume that no one is able to do division in
this limited algebra. Just think yourself back at the time when you had just
learned multiplication, but not division. With this limited algebra we now
describe how Bob sends a message to Alice. For our example, this message is
just one number.
The procedure has three parts. First, we describe how to generate the pub-
lic and the private key; then we explain how to encrypt and decrypt messages.
Construction of the Keys
First we need the keys, the private and the public one. The message is going
to be sent from Bob to Alice. Thus, Alice needs the private key to decrypt the
message. To get this private key, Alice thinks up two numbers and multiplies
them. The first of the two numbers becomes the private key. The other one
and the product are the public key. Thus, the private key is just one number
and the public key consists of two numbers, the public factor and the public
product.
