Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

130 Rolf H. M¨ohring and Martin Oellrich

numbers fast. Since primes possess no proper divisors, none can be found

fast and thus the factorization problem cannot be broken down. Large

primes are hard to recognize and therefore qualify as building bricks for

encryption methods. However, primes with 100 or more digits cannot be

practically handled by means of prime tables. For this purpose, other

methods generate numbers of this magnitude directly.

4. Chapter 20 (Hashing)

In Chap. 20, the main topic is also not prime numbers. Yet for most pur-

poses, hash tables of prime length are advantageous. Hash functions of the

form key value modulo table length generally have good distribution prop-

erties when the keys are uniformly distributed. A certain lookup method

called double hashing can in this way assert to ﬁnd any free entry. For

the purpose of selecting a suitable prime for a hash table, a prime table

is very useful.

5. A twin prime is a pair of prime numbers with a diﬀerence of exactly two.

The ﬁrst such pairs are: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43),

(59, 61), (71, 73),.... The very ﬁrst one (3, 5) is an exception for two rea-

sons. First, the number 5 is the only one to occur in two pairs. Second, in

all other twins, the number between the primes is divisible by 6. This must

be the case, since among three contiguous numbers exactly one must be

divisible by 3 and at least one by 2. The two primes (except with (3, 5)) are

neither divisible by 2 nor by 3, therefore the middle number contains both

factors. Twin primes have been found in arbitrary large ranges of natu-

ral numbers. However, there is still no proof whether ﬁnitely or inﬁnitely

many of them exist. In a prime table up to 10

, we can ﬁnd 3,424,506 such

twins.

One-Way Functions. Mind the Trap – Escape

Only for the Initiated

R¨udiger Reischuk and Markus Hinkelmann

Universit¨at zu L¨ubeck, L¨ubeck, Germany

The contributions so far have shown how a speciﬁc algorithmic problem can

be solved fast – slightly more generally, computer scientists use the term

eﬃciently. If we cannot ﬁnd a fast algorithm one might be tempted to feel

unhappy. Here we show that problems that are not eﬃciently solvable can still

be very valuable. Thus, we like to phrase the message of this article as

bad news can turn out to be quite useful.

The Mirror Image of Multiplication: Factorization

In Chap. 11 it is shown that the product of numbers can be computed very

fast, even when the numbers are quite big and therefore require many decimal

or binary digits to write them down. A simple algorithm for multiplying two

numbers is taught at elementary school. This way, a human being can compute

the product of two larger numbers on a piece of paper in a few minutes, even

if it might be boring and require concentration to avoid errors. For computers

it is one of the easiest tasks to multiply numbers with hundreds or thousands

of digits in a few milliseconds.

Let us consider the inverse problem: to split a product back into its factors.

Remember that certain numbers, called primes, cannot be divided further

into a product of smaller numbers, and that the ﬁrst prime numbers are

2, 3, 5, 7, 11, 13, 17, 19, 23,.... Mathematicians have shown that every natural

number uniquely can be expressed as a product of primes, for example,

20,518,260 = 2 · 2 · 3 · 5 · 7 · 7 · 7 · 997.

Naturally, the question comes up to design an algorithm that ﬁnds this se-

quence of divisors, the factorization problem. Can we do this as eﬃciently

as multiplication, even for large numbers?

The last digit of a decimal number N tells us whether it can be divided by

2 or 5. Divisibility by 3 can be decided by adding the digits of N. For numbers

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

14,

 Springer-Verlag Berlin Heidelberg 2011

132 R¨udiger Reischuk and Markus Hinkelmann

Fig. 14.1. A one-way function

that have only large prime divisors, however, ﬁnding the divisors does not seem

to be that easy. The ancient Greeks knew a method: test N with all primes

p that are at most as large as the square root of N. However, for a 100-digit

number this requires about 8.5 · 10

division tests, which is incredibly many

and would last longer than the expected lifetime of our universe.

A simpler variant of the factorization problem is the prime number prob-

lem, where one has to ﬁnd out whether a given number is already prime and

thus has no smaller divisors. Eﬃcient algorithms are known for the prime

number problem, so this will not be the topic here – see Chap. 13.

In the 1970s three computer scientists, Ron Rivest, Adi Shamir and

Leonard Adleman, invented the RSA cryptosystem. It encrypts texts to

be sent over an insecure communication medium like the Internet such that

a third person is not able to ﬁnd out the contents of the message. Nowadays,

the RSA cryptosystem is used worldwide as a basic tool for secure Web trans-

actions. It selects a number N that is the product of two large primes p and q,

but keeps these two factors secret. Breaking this encryption scheme is closely

related to ﬁnding out the factors p, q of N.

In order to demonstrate how secure their system is, in 1977 the inventors

encrypted a message with a 129-digit decimal number N . They then made

N and the encrypted message public, challenging everybody to decrypt the

message, where

Fig. 14.2. How can we get back?

14 One-Way Functions 133

N =

114381.625757.888867.669235.779976.146612.010218.295721.242362.562561.842935.

706935.235733.897830.597123.563958.705058.989075.147599.290026.879543.541

It took 17 years until in 1994 very complex algorithms had been developed

that were more clever than simply testing all possible prime divisors. After

eight months of intensive computing on a worldwide cluster of hundreds of

computers, ﬁnally the two factors

N = 3490.529510.847650.949147.849619.903898.133417.764638.493387.843990.820577

× 32769.132993.266709.549961.998190.834461.413177.642967.992942.539798.288533

were found. In total, about 160 trillion computer instructions were executed,

that is 1.6 ·10

. Are you interested in knowing the encrypted message? “The

magic words are squeamish ossifrage.”

One-Way Functions

Today, 16 years after this event:

• The bad news: even with the best algorithms known and the fastest super-

computers available now or in the near future, and using many thousands

of such machines together, for a decimal number with several hundred

digits that has only large prime factors one cannot ﬁnd these factors in

acceptable time (for example, within 100 years).

• The good news: as long as no new factoring algorithms are found that are

dramatically faster, data encrypted with the help of the RSA-scheme – for

example, passwords during online banking – can be considered absolutely

secure.

Let us summarize so far:

1. The multiplication of numbers, in particular prime numbers, can be done

quite eﬃciently.

Fig. 14.3. Return through a secret door

134 R¨udiger Reischuk and Markus Hinkelmann

2. Its inverse operation, splitting a product back into its prime divisors,

cannot be done eﬃciently – at least according to the current state of

knowledge in informatics and mathematics.

How can we make use of such a situation in general? In mathematics, the

term function denotes an operation that transforms mathematical objects into

other objects. In our case, the objects are numbers or sequences of numbers.

Factorization can be considered as the inverse function to multiplication.

An operation that can be computed easily, but for which the inverse is

diﬃcult is called a one-way function. Such functions are important for the

encryption of messages. Instead of sending the original message M one could

send the result of applying the one-way function to M . The encryption can

be done fast, whereas the decryption, that is, applying the inverse function,

is very diﬃcult according to the properties of one-way functions. An attacker

thus has no chance to deduce M from its encryption.

Consider the following example. Alice wants to send to Bob the message

“top secret”. Let us assume that they use only capital letters and instead of a

space between two words write the letter “X”. The letters are then numbered

with 01 up to 26 and each letter is replaced by its number. Then

TOPXSECRET

turns into

T = 201516240503180520.

In general, T will not be prime; however, by adding a few digits at the right

end one can always make this number prime – in our case, for example, using

the digits 13 we get the prime number

p = 20151624050318052013.

Then Alice chooses a second slightly larger prime number, for example,

q = 567891624050318052137

and computes their product

N = p · q = 11443938509186566743788165964622411801781.

This number N can be sent by Alice to Bob without any worry – nobody will

be able to decipher the message p,resp.T since this would mean that the

factorization of N has been found. To be honest, these numbers are too small

to guarantee high security – in reality one should choose prime numbers with

at least 150 digits, thus Alice simply adds more digits to T to generate a p

that is long enough.

But, wait, even Bob cannot decrypt the message. Grrrrr . . . encryption

with one-way function is not totally simple. We need an additional trick.

A one-way function f with secret information, in technical terms a

trapdoor function, has the following additional property:

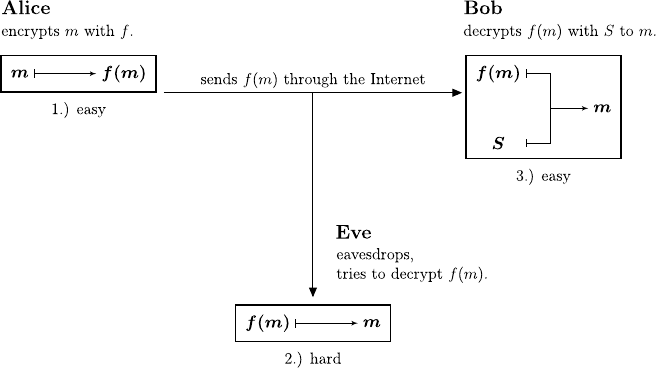
14 One-Way Functions 135

Fig. 14.4. Using a trapdoor function in cryptology

3. The inverse function of f can be computed eﬃciently if one possesses a

secret key S.

This requirement may sound strange at ﬁrst thought; however, we can

illustrate it with a simple example from our daily life.

A Practical Problem: Searching a Telephone Book

Let’s take a step back into history when telephone numbers where not available

online in electronic databases, but had to be looked up in printed telephone

books. If Alice wants to call her old friend Bob after a long time, but does not

have his current number, she only has to search for his name in the telephone

book and then ﬁnd the number behind Bob’s name. This is simple and fast –

why?

Remember Chap. 1 on binary search. The telephone book for the German

city L¨ubeck, for example, has about n = 250,000 entries, which means that

with at most 18 ≈ log

n many comparisons of names one can ﬁnd Bob since

the names are listed in alphabetical order. If they were not ordered one would

have to read the telephone book from the beginning and compare every name

until Bob is found. On average, this will require about half the book size

since Bob could be anywhere. For a midsize city like L¨ubeck this would be

completely impractical (instead of transmitting her invitation for a dinner

in the evening to Bob over the phone, Alice would still be searching for his

number the next morning). Although searching in telephone books rarely is

done by a perfect binary search – even by computer scientists – everybody

knows from experience: searching for telephone numbers is easy because of

the alphabetical ordering.

136 R¨udiger Reischuk and Markus Hinkelmann

Fig. 14.5. Normal telephone book

What about searching the other way, for a given number ﬁnd the owner

of this number?

Alice ﬁnds on the display of her telephone that somebody with the

number 123456 has tried to call her while she was away. She cannot

remember this number, thus would not like to call back right away,

but ﬁrst ﬁnd out whom to expect at the other end.

Having available only a printed telephone book she has no other choice than

scanning the book entry by entry until she ﬁnds the number. Thus the map-

ping name → number is a one-way function, at least for human beings only

having access to printed telephone books.

Computers, however, can sort a sequence of data pairs with clever algo-

rithms very fast (as explained in previous articles) such that nowadays infor-

mation providers also oﬀer telephone books ordered by numbers. With the

help of such an inverted telephone book one can now search for names given

the numbers very fast, too, again exploiting binary search. Thus, in our mod-

ern times one could also solve this problem eﬃciently. But for a moment let

us stick to the situation where only standard telephone books are available.

A nice telephone company could solve Alice’s problem by assigning num-

bers to customers according to their alphabetical ordering. For example, Alice

gets a number m

that is smaller than Bob’s number m

since her name pre-

cedes Bob in alphabetical order. In such a system we can ﬁnd names in a few

seconds if we perform binary search with respect to the entries of numbers.

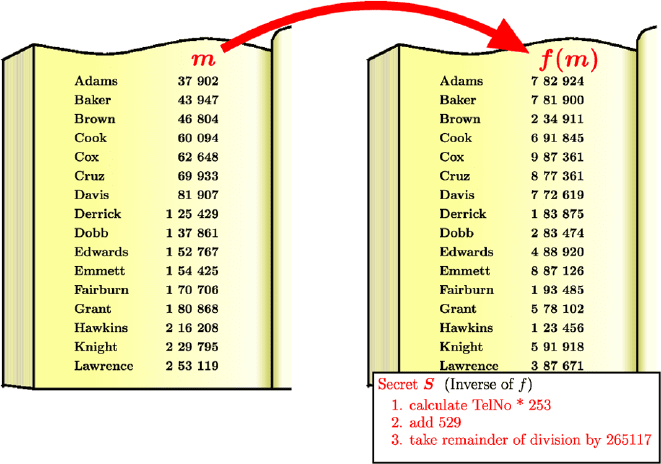
14 One-Way Functions 137

Fig. 14.6. Telephone book ordered by numbers and book with numbers transformed

A telephone book for an ordered number system thus has lost its one-

way property. Bob, who is concerned about protection personal information,

does not like such a system. He demands to keep the “practical” anonymity

of a caller even if his number is displayed, and thus requests to stick to a

chaotic distribution of telephone numbers. Therefore, he asks the international

society of cryptologists (ISCRY) for help. The ISCRY solves the problem by

assigning new numbers to all people. The new numbers are obtained by a

secret transformation h of their numbers in the ordered system such that the

originally ordered sequence of numbers

Andreas

Axel

... of Alice, Andreas, Axel, ...

after transformation to

h(m

) h(m

Andreas

) h(m

Axel

) ... looks completely chaotic.

ISCRY, however, knowing the transformation, can recompute the original

number m from h(m) and perform a binary search on these recomputed num-

bers.

The mapping name → number in the transformed telephone book is there-

fore a one-way function with a secret key, the transformation h.Everybody

can easily ﬁnd the number for each name. The inverse search, however, can

only be done eﬃciently by those who know the secret transformation h.

138 R¨udiger Reischuk and Markus Hinkelmann

Table 14.1. Numbers are estimated and rounded

Subject Computation time / Numbers

Using the fastest algorithms known today

and all computers on earth for:

Factoring a 256-digit decimal number More than 2 months

Factoring a 512-digit decimal number More than 10 million years

Factoring a 1024-digit decimal number More than 10

years

Lifetime of our universe ≈ 10

years

Cycles of a 5-GHz processor in 1 year ≈1.6 · 10

Number of electrons in our universe ≈8 · 10

Number of 100-digit primes ≈1.8 · 10

Security and Googles

Can one make sure for a speciﬁc problem that there is no eﬃcient algorithm

to solve it? Intuitively, it seems more diﬃcult to prove the nonexistence of

an object than its existence since in the latter case one only has to present

it.

This is surely true when searching for fast algorithms since there are po-

tentially inﬁnitely many (compare the discussion in Chap. 24).

To remove any last doubts concerning the security of modern cryptosys-

tems, one has to prove that there do not exist eﬃcient algorithms for the

inverse of an encryption function. More than 30 years’ research in informat-

ics has tried to develop methods for analytical proofs that certain problems

cannot be solved eﬃciently. Although some milestones have been met, there

still seems to be a long way to go to reach this goal.

Finally, we would like to give the reader some feelings for big numbers. Ta-

ble 14.1 contains estimations for the time to factor a number that is composed

of two big primes. For comparison, some physical constants are added.