Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

190 Martin Dietzfelbinger

Protocol Text Comparison by Fingerprinting

Alice has the sequence T

=(a

,...,a

) of numbers between 0 and d − 1.

Bob has the sequence T

=(b

,...,b



) of numbers between 0 and d − 1.

1. Alice tells Bob what n is. If n = n



, Bob says “diﬀerent,” and STOP.

2. Alice and Bob agree on a number k of repetitions.

3. Alice ﬁnds some prime number m a little larger than d and 10n.

She chooses k numbers r

,...,r

between 1 and m − 1atrandom,

and tells Bob m and r

,...,r

4. Alice calculates FP

),...,FP

(For this, she modiﬁes algorithm FP in such a way that

the text T

is only run through once to calculate all k results.)

5. Bob calculates FP

),...,FP

) in the same way.

6. Alice tells her k results to Bob.

7. Bob compares with his k values.

If there are diﬀerences, he says “diﬀerent,” and STOP.

If all values are equal, he says “can’t see a diﬀerence,” and STOP.

One can say the following about the result of the protocol.

• If Alice and Bob have the same text, then the sequences of k ﬁngerprints

they calculate are the same. Hence the result always is “can’t see a diﬀer-

ence.”

• If Alice and Bob have diﬀerent texts (of the same length), then by the Fin-

gerprinting Theorem, among the m −1 numbers Alice chooses from, there

are at most n−1 many values for r that make FP

,r)andFP

,r)

coincide. For r randomly chosen, the probability that FP

,r)and

,r)areequalisatmost(n − 1)/(m − 1). The probability that

Alice chooses such “bad” r’s in all k trials, making Bob say “can’t see a

diﬀerence” erroneously, is no larger than

(n − 1)

(m − 1)



n − 1

m − 1







Since we have assumed that m ≥ 10n, the bound is smaller than 1/10

and by choosing k large enough Alice and Bob can adjust the error probability

bound to as tiny a value as they wish.

If m ≈ 10n,andn has exactly l decimal digits, and Alice and Bob want the

error probability to be at most 10

−k

, it is suﬃcient that Alice communicate

(l +1)· (2 + 2k) digits. It is astonishing that this ﬁgure changes only very

slowly when the length of the text is increased: When comparing texts that

are ten times as long, i.e., n increases by a factor of ten, the number of digits

that have to be communicated increases only by 2k.

19 Fingerprinting 191

Summary

• If one wants to have absolute certainty when comparing two texts, one

may use “lossless data compression” techniques, but normally it will not

be possible to save more than a factor of 5 or so over the full length of the

text.

• If it is acceptable that one erroneously comes to the conclusion that two

texts are the same with a (very) small probability, ﬁngerprinting techniques

can be employed. This will dramatically reduce the length of the messages

to be transmitted.

• For texts of length n, a prime number m>nis used. When sending k

ﬁngerprints, the error probability is no larger than (

)

. In this case,

2k + k numbers not larger than m must be transmitted.

• Using randomness in algorithms and communication protocols can lead

to signiﬁcant savings in resources such as storage space or transmission

time if it is acceptable that with some small probability a wrong result

occurs. More often than not, by simple means (such as repeating the al-

gorithm/protocol) the error probability can be made so small that errors

can be practically eliminated.

• Algorithms and protocols that use randomness to make some decisions or

choices are called “randomized.” In Chap. 25 it is discussed how “random-

ness gets into the computer,” i.e., how one gets the computer to produce

“random” numbers.

• Sometimes very abstract mathematical facts that at ﬁrst glance look nice

but do not seem to have a practical value can be utilized in order to save

computing cost, storage space, or communication cost.

Remarks on the Fingerprinting Theorem

For the mathematically interested reader, we now give an informal argument

that makes it plausible for the Fingerprinting Theorem to be true.

For this, we consider “polynomials,” more precisely “rational polynomials.”

These are expressions

f(x)=c

+ c

n−1

+ ···+ c

x + c

with a “variable” x,wherethe“coeﬃcients” c

n−1

,...,c

are rational

numbers, or fractions p/q,withp, q integers and q>0. For example, the

following expressions are rational polynomials:

x −

+4x

− 3x

−

x +

, 0.

In the second to last example (

)wehaven =0andc

;inthelast

example (0) there are no nonzero terms at all. When writing polynomials,

terms c

with c

= 0 are usually omitted.

192 Martin Dietzfelbinger

Polynomials may be added and subtracted by applying the usual rules:







−3x

x − 1



=(2− 3)x

x +



− 1



= −x

x +





−



−3x

x − 1



=(2+3)x

−

x +





=5x

−

x +

If one subtracts a polynomial f(x) from itself, the result is the “zero poly-

nomial”: f(x) − f(x) = 0. Of course, one may also multiply polynomials.

For this, one expands the product by the distributive law and then collects

coeﬃcients that belong to the same power of x.Hereisanexample:

(2x

) · (

− x)=

− 2x

−

x =

−

Another important operation with polynomials is “substitution”: If f(x)isa

polynomial and r is a rational number, we write f(r) for the result that is

obtained by substituting r for x in f(x) and evaluating. That means that if

f(x)=x

−

+2x − 1, then f(0) = −1andf (

)=0andf(1) =

A rational number r is called a root of a polynomial f(x)iff (r)=0.For

example, r =

is a root of f (x)=x

−

+2x − 1.

Of course, the zero polynomial 0 has inﬁnitely many roots, namely, all

rational numbers. The polynomial f(x) = 10 has no roots at all, and the

polynomial 2x + 5 has exactly one root, namely r = −

. The polynomial

− 1 has two roots, namely 1 and −1, and the polynomial x

+1 hasno

(rational) roots. One can prove the following:

Theorem (Number of Roots of Rational Polynomials)

If f(x)=c

+ c

n−1

+ ···+ c

x + c

with n ≥ 0andc

=0isa

polynomial, then f has at most n distinct roots.

(Roughly, the reason for this is the following: If r

,...,r

are k distinct roots

of f(x), one can write f(x) as a product (x − r

) ···(x − r

) · g(x), for some

polynomial g(x) = 0. Since the highest power of x in f (x)isx

,thenumber

k cannot be larger than n.)

From the theorem about the roots we can conclude the following: If

g(x)=c

+ c

n−1

+ ···+ c

x + c

and

h(x)=d

+ d

n−1

+ ···+ d

x + d

are diﬀerent polynomials, then there are at most n diﬀerent numbers r that

satisfy g(r)=h(r). Why is that so? Consider the polynomial

f(x)=g(x) − h(x)

=(c

− d

+(c

n−1

− d

n−1

+ ···+(c

− d

)x +(c

− d

It could happen that c

= d

,andc

n−1

= d

n−1

,andsoon,sothatmany

coeﬃcients in f(x)are0.Butsinceg(x)andh(x) are diﬀerent, f (x) cannot

be the zero polynomial, and we can write f(x)=e

+ ···+ e

x + e

,with

0 ≤ k ≤ n and e

= 0. By the theorem on the number of roots, we conclude

19 Fingerprinting 193

that f(x) does not have more than k ≤ n roots. But for each r we have that

if g(r)=h(r), then f(r)=g(r) − h(r) = 0, and hence r isarootoff(x).

Hence, there cannot be more than n numbers r with g(r)=h(r).

Hey – this is almost the formulation of the Fingerprinting Theorem! The

only diﬀerence is that in the Fingerprinting Theorem we are talking about

calculations modulo some prime number m, and here we consider calculations

with rational numbers. However, for the theorem about the number of roots

of a polynomial to be true we do not really need the rational numbers, but

only a domain of numbers in which we can add, subtract, multiply, and divide

(by any element that is not zero). One can show that arithmetic modulo m

has this property if and only if m is a prime number. This means that the

theorem about the number of roots holds in modular arithmetic modulo a

prime m as well.

Further Reading

1. J. Hromkoviˇc: Design and Analysis of Randomized Algorithms. Springer,

Berlin, 2005.

This book describes many randomized algorithms, protocols, and methods

as well as the fundamentals of the design and the study of such methods.

2. For readers who want to know all the details, a complete proof of the

Fingerprinting Theorem from ﬁrst principles can be found on the page

http://eiche.theoinf.tu-ilmenau.de/fingerprint/

3. A complete description of the ASCII code, and much more information

about it, can be found at http://en.wikipedia.org/wiki/ASCII

4. A list of prime numbers with size about 2

,1≤ k ≤ 400: http://primes.

utm.edu/lists/2small/0bit.html

Acknowledgement

Many thanks to J.D. for help with the illustrations.

Hashing

Christian Schindelhauer

Albert-Ludwigs-Universit¨at Freiburg, Freiburg, Germany

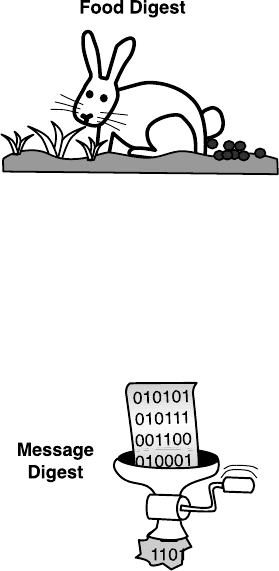
Some Germans have problems distinguishing between hashing and H¨aschen

(bunny).

Bunnies are hard to ﬁnd. These shy animals hide very well. A careful observer

may spot the following tracks on a snow-covered ﬁeld:

Here, two bunnies hopped next to each other in the snow. A track can tell

a lot about an animal: The size and weight, whether it travels in a group and

much more. Sometimes a track comes with something like this:

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

20,

 Springer-Verlag Berlin Heidelberg 2011

196 Christian Schindelhauer

Such droppings are the excrement of a bunny or hare. The droppings tell

us what the animal has eaten, whether it is healthy and many other things.

Nowadays each individual animal can be identiﬁed from it using complicated

lab tests. This method may serve also for other animals (and in Madrid canine

environmental polluters are identiﬁed this way).

Message Digest

What is the connection to algorithms? Well, the droppings come from the

food eaten by the bunny.

The food is hashed, mixed, digested, dehydrated and deposited; the result

is a small heap. This product can be mapped back to the food. A lot of

information is lost: the (digestive) path, yet the food can still be identiﬁed.

Something similar can be done with text documents, music ﬁles and video

ﬁles. For computer engineers these are just series of bits, being either zero or

one. Such a sequence is mixed, merged and compressed into a bit sequence of

ﬁxed length. We say the bit sequence is hashed. This may look like this.

A well-known algorithm for hashing is MD-5 (Message Digest 5). It was de-

veloped in 1991 by Ronald Rivest, and an accurate description can be found in

Wikipedia (http://en.wikipedia.org/wiki/MD5). Other known algorithms

are Secure Hash Algorithms 1, 224, 256, 284, and 512 (SHA-1, SHA-224, SHA-

256, SHA-384 and SHA-512 – http://en.wikipedia.org/wiki/SHA-1). They

serve the same purpose as the message digest algorithm.

20 Hashing 197

Secure Hashing

What purpose do these hash algorithms serve? First, they map ﬁles of diﬀerent

lengths onto bit sequences of the same length. Second, the result helps to

identify the original ﬁles, but does not necessarily allow us to reconstruct the

original. The mathematical description of the identifying feature follows.

By {0,1}* we describe the set of all bit sequences, which is {0, 1, 00, 01, 10,

11, 0000, 0001,...}, as well the empty bit sequence, which is no bit at all.

By { 0,1}

we describe the set of all bits of length exactly k bits: {000, 001,

010, 011, 100, 101, 110, 111} in the case k = 3. A hash function is a map-

ping:

f : {0, 1}

∗

→{0, 1}

What does it mean that the result of a hash function identiﬁes the in-

put? It means that f (x)=f(y) if and only if x = y. The opposite state-

ment is that there are two diﬀerent values x and y such that f (x)=

f(y).

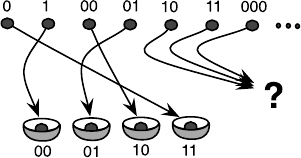
Such an equation is called a collision. We claim that a hash functions exists

where all inﬁnitely many bit sequences never collide. Mathematically this is

complete rubbish. Why?

Imagine as many bins as we have bit sequences of length k.Sowehave

bins: two possibilities for each bit. We claim that in every bin f(x)only

one original bit sequence is deposited. However, there are many more than

sequences, namely inﬁnitely many. So, at least one of the bins experiences

inﬁnitely many collisions.

But there is a loophole! We choose k so large that we have enough bins for

every ﬁle that ever may be created. So that for each ever-to-be-created ﬁle on

each ever-to-be-built computer on this planet one hash value is reserved. This

trick is used in Chap. 14 where one-way-functions are presented. For example,

choose k = 512. Then there are 2

512

> 10

154

bins. If we succeed in ﬁlling these

bins such that nobody (human or machine) can construct a collision, we are

done.

198 Christian Schindelhauer

To this day it is not clear whether such a feat is possible, although we have

candidates for hash functions like SHA-512 (512 bits for each hash value). But

this is of little value. For example, MD-5 is seen as collision free for all existing

ﬁles until a method is found to produce arbitrarily many collisions.

Practically collision-free hash functions are so useful that computer engi-

neers choose to work with these candidate functions. For example, they can

be used to prove the correctness of ﬁle transmissions. For this, the hash value

can prove that no single bit was lost or altered by the transmission, nor did

somebody exchange the whole message.

Hashing for Dictionaries

Hash functions can be used not only for storing data hash functions. Consider

a storage S for storing m data items. This storage is organized as a table

or array. So, the storage positions S[1],...,S[m] can be directly accessed to

retrieve a data item. We want to save the data items into S, which is identiﬁed

by a bit sequence (or a text).

For example,

Name Total number

German Black Forest winter snow bunny 12

European ﬁeld forest and meadow fox 2

Small stinger hedgehog 4

Big brown scary bear 1

The data is quite compact, while the search index is very long. If we had a

hash function which maps to an interval {1, 2, 3,...,m}, it would look like

this.

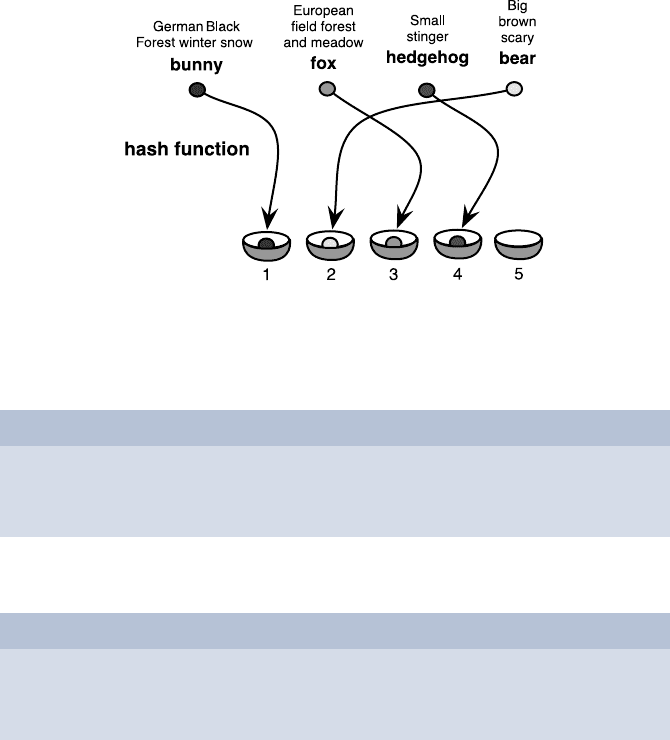
20 Hashing 199

Now we could store at the storage position S[f(“. . . bunny”)] the value 12

in this hash table, at the position S[f (“. . . fox”)] the value and so on. This

operation is named Put.

Put

1 procedure Put (string x,intz)

2 begin

3 S[f (x)] := z

4 end

Get returns the value where the value 0 denotes that no data has been

stored.

Get

1 procedure Get (string x)

2 begin

3 return S[f (x)]

4 end

Unfortunately, these functions work correctly only if the hash function is

without any collisions. So, for example, bunny and hedgehog are not mapped

to the same storage position. This can be guaranteed only for small m,ifthe

keys are known in advance (like here with bunny, fox, hedgehog and bear)

and a so-called perfect hash function has been chosen.

If one does not know the keys in advance, empty positions must be found.

For this, several methods are at hand. The easiest method is the so-called

linear probing. Then, in addition to the data, also the key must be stored.

Storing a Data Item z with Key x

First we compute the hash value f(x)ofx.IftheS[f(x)] is already occupied,

the right neighbor is tested (f(x) + 1), and its right neighbor, until an empty