Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged
Подождите немного. Документ загружается.


Overview
Helmut Alt and R¨udiger Reischuk
Freie Universit¨at Berlin, Berlin, Germany
Universit¨at zu L¨ubeck, L¨ubeck, Germany
Strategic thinking and planning are commonly regarded as typically human
capabilities. Ever since computer programs demonstrated that they can beat
chess grand masters, however, one can see that some of these skills can be
successfully managed by machines. On the other hand, some games can be
won with very simple strategies, one must have the right knowledge. In a
chapter in this part of the book we see this demonstrated impressively by the
match game Nim.
In many games, it is important that we don’t allow the enemy to antic-
ipate our moves. A simple strategy – referred to in computer science jargon
as deterministic – can, however, be predicted. This can be avoided if you in-
clude random decisions – without this many games such as rock–paper–scissors
would be quite boring. Many algorithms can be improved or be speeded up
in this way – these are called probabilistic or randomized algorithms. Now we
need to ask ourselves how a computer could toss a coin, given that we would
expect only full precision? The chapter here on random numbers provides an
answer.
A strategic and algorithmic approach makes sense even with everyday
problems, and not just during games. For example, if we wish to disseminate a
message to a broad group of people through phone calls or to many computers
via an electronic network, then we need a good plan in order to achieve this
objective quickly and reliably. We see this in the chapter on broadcasting. In
a further chapter we see a clever approach to determining the winner of an
election.
Some tasks require careful long-term planning. An example is the game
schedule for the Bundesliga, the German soccer league, which requires us to
consider various constraints.
Two chapters in this section deal with simulations, i.e., simulating natural
processes using computers. First we consider a problem from physics. We see
how to calculate the heat distribution in a metal rod or plate using so-called
Gauss–Seidel iteration. In the other chapter we consider a theme from biol-
ogy. We see how one can determine how closely two organisms are related to
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0,
c
Springer-Verlag Berlin Heidelberg 2011
222 Helmut Alt and R¨udiger Reischuk
each other from their genetic information (DNA); and we see from mutations,
minimal changes in the genetic heritage, how far apart they are from each
other or from a common ancestor.
The famous mathematician Leonhard Euler posed the K¨onigsberg Bridges
Problem: Can you cross all seven bridges exactly once on a walk and then
return to the starting point? This playful question – by the way, the answer is
“No”! – has important applications, such as in route planning, covered in the
chapter on Eulerian circuits. In vehicle navigation we are now accustomed to
a friendly voice that offers directions or tells us the distance to travel before
the next turn. For a long time natural speech was an unsolved problem for
computers. In this part of the book we see that even pronouncing long numbers
involves considerable computational effort.
Finally, we consider a problem in computer graphics. Draw a circle as
round as possible on a screen, realized using a grid of individual pixels. Strictly
speaking we cannot draw a slanted or curved line, as we could with paper and
pencil. However, a detailed analysis of the problem leads to surprisingly easy
and fast solution algorithms.
22
Broadcasting – How Can I Quickly
Disseminate Information?
Christian Scheideler
Universit¨at Paderborn, Paderborn, Germany
In the Middle Ages, there was no mass media like TV or radio. As most
people were not able to write or read, information was mostly disseminated
on a mouth-to-mouth basis, and since the travel speed of humans was quite
restricted at those times, the spreading of information was mostly bounded
by the speed of horses (though other means like pigeons and smoke or light
signals were also used occasionally). Nowadays, the telephone and other media
like the Internet allow anyone to spread information very quickly around the
world. Let us consider a specific example here.
Steffi has just been given the task to organize a party for her class, and
this at a time when the school holidays have just started! Now, she has to try
to reach all fellow students by phone or email. Unfortunately, Steffi does not
know their email addresses, but she has a list of all 121 students with their
phone numbers which was recently given to every student (and that hopefully
no one has thrown away yet!). Now, Steffi could try to do 120 phone calls,
which would consume a lot of time. Hence, she thinks about an alternative
approach to reach all students as quickly and cheaply as possible.
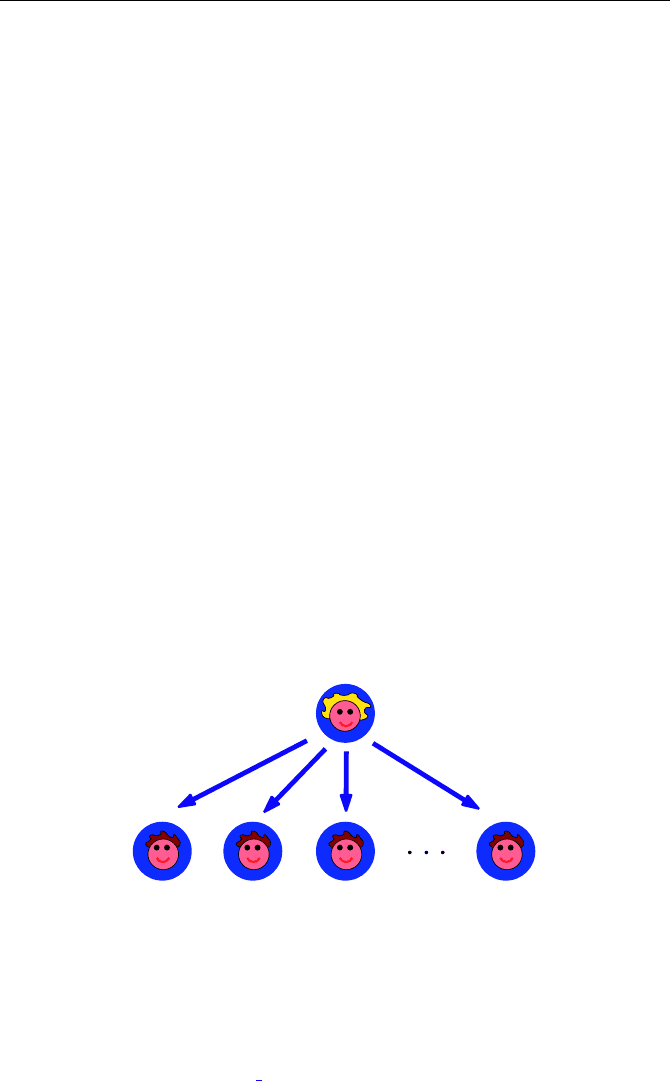
Strategy 1: Call everybody directly
B. V¨ocking et al. (eds.), Algorithms Unplugged,
DOI 10.1007/978-3-642-15328-0
22,
c
Springer-Verlag Berlin Heidelberg 2011
224 Christian Scheideler
The first strategy that comes to her mind is the silent post game: she just
calls the first person on the list and asks him or her to call the next one on
the list, who will then call the next one, and so on, until everybody on the
list has been reached.
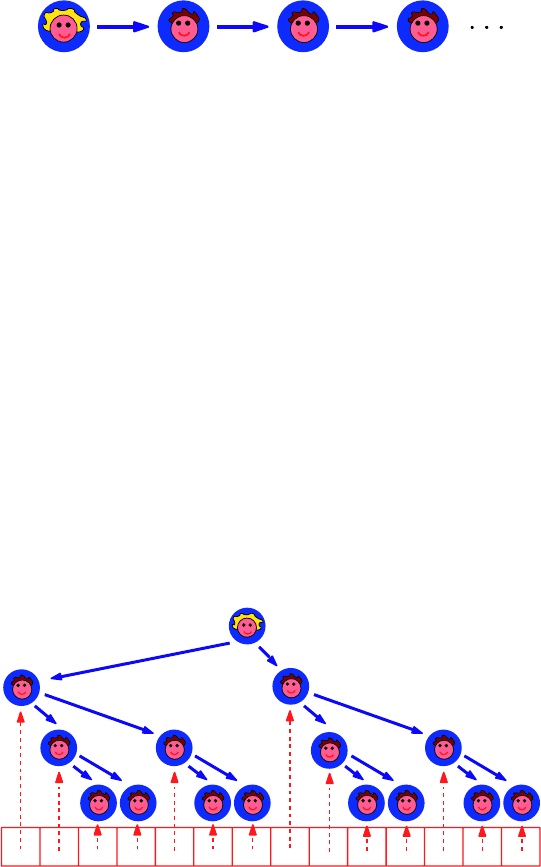
Strategy 2: Silent post
The advantage of this strategy is that every student only has to make one
call. However, since the calls have to be performed one after the other, a very
long time can go by until all students have been reached. In fact, if just 10%
of the students do not reach the next one on the list within the same day they
were called, it takes at least 12 days until everybody has been informed. Even
worse: if someone does not bother to call the next one on the list, the whole
system will break down! Thus, Steffi thinks about an alternative approach.
Since she is interested in computer science, she recalls a sorting method
that has also been presented in Chap. 3. There, a master uses two helpers to
cut a sorting problem into two smaller sorting problems, who themselves use
two helpers each to cut their sorting problems into even smaller problems,
and so on, until just one element is left. Something similar to that should also
work for the distribution of calls! For example, Steffi could divide the phone
list into two halves and call the first person on each of the two halves. Each
of them will then be asked to cut their list into two further halves and call
the first person on these halves. This is continued until everybody has been
called, i.e., we reach a level in which people are called who just have to take
care of an empty list. In this way, the students can be reached much quicker.
Strategy 3: Partitioning the phone list into sublists
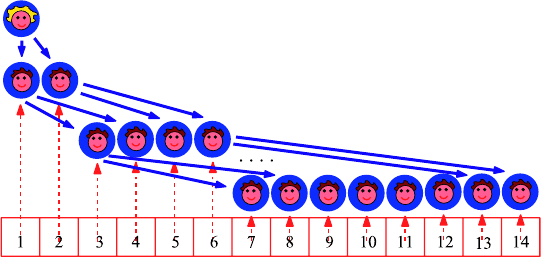
22 Broadcasting 225
Strategy 4: Everybody at list position i calls positions 2i +1 and2i +2
Indeed, Steffi determines that just seven rounds of calls are sufficient to
reach all 120 fellow students. This is much better than 120 rounds of calls!
However, her strategy sounds very technical, so it’s questionable whether the
other students can be made to adhere to the rules without errors. Thus, she
thinks about an alternative strategy.
Suppose that she calls the first two people on the list, Andi and Berthold,
and asks Andi to call the students at positions 3 and 4 while Berthold is asked
to call the students at positions 5 and 6. In general, the rule would be that
everybody at position i in the list will call the students at positions 2i +1
and 2i + 2 (if they exist). Then the information spreads at the same speed as
in the previous strategy, but the calling rule sounds now much more natural
and easy to understand.
Nevertheless, Steffi is not quite happy with her calling strategy. What if
one of her fellow students does not count right and calls a wrong pair of
students on the list? Moreover, there can still be a couple of students who
just forget or do not bother about calling their pair on the list. In this case,
some students would not be informed, who would then be mad at Steffi!
Therefore, Steffi thinks about a more robust strategy. One possibility
would be that everyone at list position i would call the four students at po-
sitions 2i +1 to 2i + 4. In this case, all students (except for the first four
on the list who will directly be called by Steffi) will be called by exactly two
students in the ideal case. Thus, as long as for each such pair at most one of
the students is unreliable (by not being reachable or forgetting to make the
call), all of the reliable students will still be informed. Intuitively, this can
be argued as follows: If one can select a caller for each student who works
reliably, then everybody who is reliable has a reliable call chain from himself
or herself back to Steffi (see also Fig. 22.1).
Steffi quickly realizes that this strategy can be made even more robust,
so that she can be really sure to reach everybody who is reachable: If every
student at position i calls the students at positions 2i +1 to 2i +2r for some

226 Christian Scheideler
Fig. 22.1. Chain of reliable students for Alex, if the positions 2i +1 to 2i +4 are
called
fixed r, then every student (except for the first 2r ones who are directly called
by Steffi) will be called by exactly r many students in the ideal case. Hence,
as long as at most r − 1 of these are not calling, all reliable students will still
be reached.
Now, we have come to a point where it would be helpful to conduct some
experiments. For a given number x (e.g., 10) of unreliable students, who
are assumed to be randomly distributed over the list, we want to determine
the minimum value of r for which the probability that all reliable students are
reached is still above, say, 90%. In order to determine this r, one can use the
algorithm presented below. This algorithm does not emulate the dissemination
of information (that runs concurrently in reality) but just determines whether
under the given communication rule all reliable students can be reached. For
this it suffices to run the for-loop in line 6 till N/2 since students with larger
list positions will not call any other student. The algorithm is based on an
array A that is defined as follows:
• A: array [1..N] of integers; A[i] counts, for a reliable student at position
i, the number of calls that student would get from other reliable students.
N is the total number of students.
Fig. 22.2. The r students that will call Alex in the ideal case for r =3

22 Broadcasting 227
• For every reliable student, A[i]isinitiallysetto0.
• For all unreliable students at position i, A[i] will initially be set to −r (so
that even after r calls there will not be a positive value in A[i]).
Algorithm for r-fold information dissemination
1 procedure Broadcast (r)
2 begin
3 for j := 1 to 2 ∗ r do // Steffi calls students 1 to 2r
4 A[j]:=A[j]+1
5 endfor
6 for i := 1 to N/2 do // Student i calls 2i +1 to 2i +2r
7 if A[i] > 0 then // if call has been received
8 for j := 2 ∗ i +1 to 2 ∗ i +2∗ r do
9 if j ≤ N then A[j]:=A[j]+1
10 endif
11 endfor
12 endif
13 endfor
14 // Did it work?
15 for i := 1 to N do
16 if A[i]=0then output
“not everyb
ody reached”, stop
17 endif
18 endfor
19 output “everybody reached”
20 end
After all this thinking, Steffi has more and more fun in inventing new
rules. Next, she considers the more challenging case that every student has
a different list of all the other students, so all of her prior strategies are not
applicable any more. Is there still a fast and robust strategy to reach all of
the reliable students if, say, an arbitrary quarter of the students is unreliable?
After some thinking, Steffi has the idea that she, like everybody else who
is called the first time, just randomly picks r students on the list and calls
them (see Strategy 5).
If Steffi starts with this strategy, then she will certainly inform r students
who have not already been called (if all of them are reachable). In the ideal
case, all of them are reachable and reliable, so each of them will call r other
students. Hence, at best, r
2
students will then be informed. In reality, however,
it can happen that a student is called more than once. Since every student
will become active only once (otherwise, the calls would never terminate!),
this harms the dissemination of Steffi’s information. Also, it can happen that
unreliable students are called, which will further lower the dissemination of
the information. Nevertheless, one can verify through experiments that Steffi’s
information will reach all reliable students with high probability if r is suffi-
ciently large (but still reasonably small). In order to determine this r, one can
use the algorithm below. It is based on two arrays A and C that are defined
as follows:

228 Christian Scheideler
Strategy 5: Every student, including Steffi, calls r random students for r =3
Algorithm for random r-fold information dissemination
1 procedure RandomBroadcast (r)
2 begin
3 for j := 1 to r do // calls from Steffi
4 if A[C[0][j]] = 0 then A[C[0][j]] := 1
5 endif
6 endfor
7 continue := 1 // indicator for newly called students
8 while continue =1do
9 continue := 0
10 for i := 1 to N do // search for newly called students
11 if A[i]=1then
12 continue := 1; A[i]:=2
13 for j := 1 to r do
14 if A[C[i][j]] = 0 then A[C[i][j]] := 1
15 endif
16 endfor
17 endif
18
endfor
19 endwhile
20
// Did it
work?
21 for i := 1 to N do
22 if A[i]=0then output “not everybody reached”, stop
23 endif
24 endfor
25 output “everybody reached”
26 end
• A: array [1..N ] of integers; initially A[i]=−1 if student i is unreliable and
otherwise A[i]=0.N is the number of students.

22 Broadcasting 229
• If a reliable student i is called for the first time, then A[i] is set to 1, and
once he or she has finished all calls, A[i] is set to 2.
• C: array [0..N][1..r] of integers; C[i][j] gives the number of the jth student
who is called by student i (Steffi counts here as student 0). C is chosen at
random.
Of course, one can think of many other strategies to disseminate infor-
mation in a group of people, and everybody is encouraged to do so. Which
strategy would you have chosen if you were Steffi?
References
1. http://en.wikipedia.org/wiki/Broadcasting (computing)
This Wikipedia article gives an introduction to broadcasting and to stan-
dard strategies used in this area.
2. C. Diot, W. Dabbous, and J. Crowcroft: Multipoint Communication:
A Survey of Protocols, Functions and Mechanisms. IEEE Journal on Se-
lected Areas in Communications 15(3), pp. 277–290, 1997.
K. Obraczka: Multicast Transport Protocols: A Survey and Taxonomy.
IEEE Communications Magazine 36(1), pp. 94–102, 1998.
M. Hosseini, D.T. Ahmed, S. Shirmohammadi, and N.D. Georganas:
A Survey of Application-Layer Multicast Protocols. IEEE Communica-
tions Surveys & Tutorials 9(3), pp. 58–74, 2007.
These articles are recommended for an introduction to the scientific liter-
ature on broadcasting.
3. R. Karp, S. Shenker, C. Schindelhauer, and B. V¨ocking: Randomized Ru-
mor Spreading.In:IEEE Symposium on Foundations of Computer Science
(FOCS), pp. 565–574, 2000.
This article contains advanced broadcasting methods that are more ef-
fective but also more complex than the strategies presented here. It is
recommended to everyone interested in learning about the newest results
in this field and who is not afraid of mathematical formulas.
