Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

240 Thomas Erlebach

Hannah has received the most votes, namely 14. Adam’s class has 27 pupils.

As 14 is more than 13.5 (half the class size), Hannah has won the absolute

majority and is therefore elected class rep. Hannah has already been class

rep in the previous year, and she will surely continue to do well in that role.

All the pupils and the teacher congratulate Hannah on winning the elec-

tion.

Later, Adam starts to think about the counting of the votes once more.

He wonders how good the method that he had used was. For each ballot

paper he had to look through the list of names on his sheet and add a tally

mark or even a new name to the list. Doing this for 27 votes was ﬁne, but

in a larger election that would surely become quite tedious. Just imagine an

election with hundreds or thousands of votes! The list of names could then

also get very long, and consequently it would take quite long to check for the

name on a ballot paper whether it is already in the list or not. Furthermore,

Adam’s method of counting the votes has produced more information than

was required: He didn’t just determine the winner of the election, but he also

counted the votes for each of the other candidates. The latter information

wasn’t really necessary for solving his task. Maybe it would have been possible

to avoid determining unnecessary information and solve the task with less

eﬀort?

Let us remark here that it is also often important for data protection

reasons to avoid unnecessary collection and processing of data and to gen-

erate only the information that is required to solve the task at hand; this

signiﬁcantly reduces the danger of misuse of personal data. A more detailed

discussion of data protection issues is beyond the scope of this chapter, how-

ever.

Adam has recently become interested in algorithms and knows by now

that there are often methods that are much faster than the most obvious

method for solving a task. Therefore, he decides to investigate this further

and ﬁnd out whether there is a faster method for checking absolute majority

in an election. Together with Laura, who is also interested in algorithms,

Adam searches through various books on algorithms to see if they can ﬁnd

out something about the majority problem.

Majority Algorithm

Laura and Adam indeed ﬁnd information about the majority problem, i.e., the

problem of determining from among N given elements the majority element

(the element that occurs more than N/2 times, if it exists). They come across

the description of the following algorithm.

24 Majority – Who Gets Elected Class Rep? 241

Majority Algorithm

1 Use a stack of elements that is initially empty.

2 Phase 1: Process one by one each of the N given elements and execute for

each element X the following:

3 If the stack is empty, put X on top of the stack.

4 Otherwise compare X with the top element of the stack. If X and that

element are identical, put X on top of the stack; if the two elements

diﬀer, remove the top element from the stack.

5 If the stack is empty, report that there is no majority element.

6 Phase 2: Otherwise take the top element Y of the stack and count how often

Y occurs among all N given elements. If Y occurs more than N/2times,

output Y as answer. If Y does not occur more than N/2 times, report that

there is no majority element.

Laura and Adam are surprised that this should work. That algorithm

would indeed signiﬁcantly simplify the process of determining the winner in

a large election: When processing a ballot paper, the name on the ballot

paper would only have to be compared with a single other name, namely the

name of the ballot paper on top of the stack. In the end one would have

to go through all the ballot papers a second time to count how often the

name determined in Phase 1 occurs, but that wouldn’t be too time-consuming

either. The algorithm appears very interesting, but Laura and Adam still

doubt whether it really works correctly. It seems that at the end of Phase 1 the

top of the stack might contain an arbitrary element that happened to occur

a couple of times among the last elements that were processed in Phase 1.

A completely diﬀerent element could then be the majority element. Laura

and Adam are still doubtful and decide to ﬁrst try out how the algorithm

processes a few sample inputs. For example, they consider an input consisting

of the following N = 7 elements (for the sake of simplicity, we use capital

letters to denote elements): B, B, A, A, C, A, A. The algorithm executes

Phase 1 as shown in the following table. Each line of the table represents one

step of the algorithm, and the current elements in the stack are speciﬁed in

each line by listing them in the order from the bottom to the top of the stack:

Stack Considered element Action

empty B put B on the stack

B B put B on the stack

B, B A remove B from the stack

B A remove B from the stack

empty C put C on the stack

C A remove C from the stack

empty A put A on the stack

242 Thomas Erlebach

Indeed, in the end there is an A at the top of the stack. In Phase 2 the

algorithm counts how often A occurs among the given elements. Since A occurs

four times among the N = 7 elements B, B, A, A, C, A, A, the algorithm

correctly recognizes and outputs A as majority element. Thus, the algorithm

has worked correctly for this example. One also notices that in each step the

elements on the stack are all identical; actually this has to be the case because

the algorithm puts an element on the stack only if the stack is empty or the

element is identical to the element at the top of the stack.

How does the algorithm behave if the input does not contain a majority

element, for example, if the input is A, B, C, C? Here, C occurs twice among

the N = 4 elements, but a majority element would have to occur strictly more

than N/2 times. Phase 1 of the algorithm would proceed as follows:

Stack Considered element Action

empty A put A on the stack

A B remove A from the stack

empty C put C on the stack

C C put C on the stack

C, C

This time we have a C at the top of the stack when Phase 1 ends. This

shows that Phase 2 of the algorithm is really necessary. In Phase 2 the al-

gorithm counts how often C occurs in the input. Since C occurs only twice,

the algorithm reaches the correct conclusion that the input does not contain

a majority element.

How does the algorithm deal with an input of the form A, A, A, B, B,

in which an element diﬀerent from the majority element occurs several times

near the end of the input? Even this does not fool the algorithm:

Stack Considered element Action

empty A put A on the stack

A A put A on the stack

A, A A put A on the stack

A, A, A B remove A from the stack

A, A B remove A from the stack

At the end there is an A at the top of the stack, so the algorithm ﬁnds the

correct majority element once again. Somehow the algorithm seems to always

produce the correct output, although Laura and Adam still don’t understand

completely why it actually works. They take another look at the algorithms

book. There they ﬁnd a proof for the correctness of the algorithm. At ﬁrst the

proof seems quite complicated and diﬃcult to comprehend, but Laura and

Adam go through it several times and help each other by explaining the parts

of the proof that they so far understand. Finally, they are convinced that the

algorithm always works correctly.

24 Majority – Who Gets Elected Class Rep? 243

Correctness of the Majority Algorithm

The proof of correctness of the majority algorithm can be summarized as

follows: If the algorithm outputs an element X, then that element must indeed

be the majority element, because the algorithm has veriﬁed in Phase 2 that X

occurs more than N/2 times. Thus, the only case in which the algorithm could

possibly go wrong is when the input contains a majority element X but the

algorithm wrongly reports that the input does not contain a majority element.

This can only happen if at the end of Phase 1 the stack is empty or an element

diﬀerent from X is at the top of the stack. The following considerations show

that this is impossible.

Consider an arbitrary input with N elements, among which more than

N/2 elements are identical to X. Assume that at the end of Phase 1 there

is no X at the top of the stack. As at any time all elements of the stack are

identical, this means that at the end of Phase 1 there is not a single X in the

stack. Therefore, there are only the following two possibilities for what could

have happened to each X in the input:

1. When the X was processed, the stack contained one or several elements

diﬀerent from X. The algorithm did not put X on the stack, but removed

an element Y from the stack.

2. When the X was processed, the stack was empty or contained elements

identical to X. Therefore, the X was put on the stack. Since there is no

X in the stack at the end of Phase 1, there must have been an element Z

that came after the X and caused the X to be removed from the stack.

Based on these considerations, each element X can be assigned to an element

diﬀerent from X: In the ﬁrst case X is assigned to the respective element Y,

and in the second case to the respective element Z. In addition, one can see

that no two elements X are assigned to the same element diﬀerent from X.

From this we can deduce that there were at least as many elements diﬀer-

ent from X as there were elements identical to X. Since there are only N

elements in total, this contradicts the assumption that the input contains

more than N/2 elements identical to X. Therefore, it is impossible that X

is the majority element but there is no X at the top of the stack at the

end of Phase 1. Consequently, there must be an X at the top of the stack

when Phase 1 ends, and the algorithm correctly recognizes X as majority

element.

How Many Comparisons Are Necessary?

It is also interesting to ask how many comparisons between elements a ma-

jority algorithm needs to make in order to solve the problem. Here, the term

‘comparison’ refers to the operation of checking whether two elements are

identical or not. The majority algorithm described above performs at most

244 Thomas Erlebach

N − 1 comparisons in Phase 1: The ﬁrst element is put on the stack without

a comparison, and when each of the remaining elements is processed, that

element can be compared only to the one element that is at the top of the

stack at that time. Phase 2 can also be carried out with at most N − 1 com-

parisons. Altogether the algorithm makes at most 2N − 2 comparisons if the

input consists of N elements.

The natural question now is, Can we do better, i.e., are fewer than 2N −2

comparisons suﬃcient to solve the problem? The answer is yes, because the

following variation of the majority algorithm never needs more than 3N/2−2

comparisons. (The notation . means that the value gets rounded up to the

next integer; for example, for N =5wehave3N/2 = 15/2 = 7.5 =8,

and for N =6wehave3N/2 = 18/2 = 9 =9.)

Reﬁned Majority Algorithm

1 Use two stacks of elements that are initially empty.

2 Phase 1: Process one by one each of the N given elements and execute for

each element X the following:

3 If Stack 2 is not empty and X is identical to the element at the top of

Stack 2, then put X on Stack 1.

4 Otherwise put X on Stack 2 and, if Stack 1 is not empty, remove the

top element of Stack 1 and put it on Stack 2.

5 Assume that at the end of Phase 1, the top element of Stack 2 is a Y.

6 Phase 2: While Stack 2 is not empty, repeat the following operations:

7 Compare the element at the top of Stack 2 with Y.

8 If the top element of Stack 2 is identical to Y, remove two elements from

the top of Stack 2. (If Stack 2 contains only a single element, remove it

from Stack 2 and put it on Stack 1.)

9 Otherwise (i.e., if the top element of Stack 2 is diﬀerent from Y) remove

the top element from Stack 1 and the top element from Stack 2. (If

Stack 1 was already empty and we can’t remove an element from Stack 1,

terminate and report that there is no majority element.)

10 If Stack 1 is not empty, output Y as majority element. Otherwise report

that there is no majority element.

We see that even the description of the individual steps of the reﬁned majority

algorithm is rather complicated. It is not only diﬃcult to become convinced

that the algorithm is correct, it is also a challenge to work through the steps

of the algorithm correctly for an example input. To better understand the

reﬁned majority algorithm, let us ﬁrst consider the input

B, B, A, A, C, D, A, A, A

and see how the algorithm executes Phase 1 (in each line, the contents of the

two stacks are listed in the order from bottom to top):

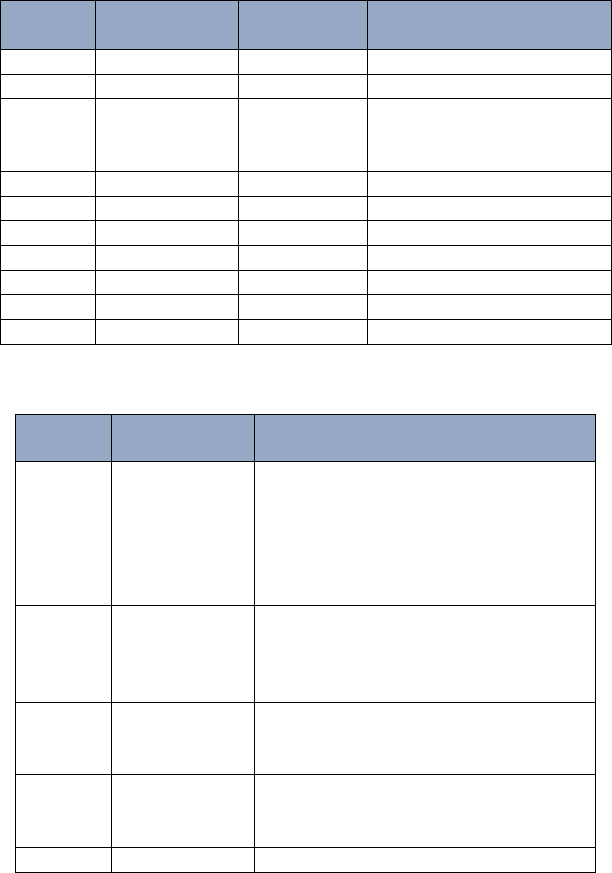
24 Majority – Who Gets Elected Class Rep? 245

Stack 1 Stack 2 Considered Action

element

empty empty B put B on Stack 2

empty B B put B on Stack 1

B B A put A on Stack 2,

remove one B from Stack 1

and put it on Stack 2

empty B,A,B A put A on Stack 2

empty B,A,B,A C put C on Stack 2

empty B,A,B,A,C D put D on Stack 2

empty B,A,B,A,C,D A put A on Stack 2

empty B,A,B,A,C,D,A A put A on Stack 1

A B,A,B,A,C,D,A A put A on Stack 1

A,A B,A,B,A,C,D,A

Indeed, the majority element A is at the top of Stack 2 when Phase 1 ends.

Phase 2 now executes as follows:

Stack 1 Stack 2 Action

A,A B,A,B,A,C,D,A The element at the top of Stack 2 is

identical to A (this must be the case,

because A was chosen to be the ele-

ment that was at the top of Stack 2

when Phase 1 ended), so remove the

two elements (D,A) from Stack 2

A,A B,A,B,A,C The element C at the top of Stack 2

is diﬀerent from A, so remove one el-

ement from Stack 2 and one element

from Stack 1

A B,A,B,A The element at the top of Stack 2 is

identical to A, so remove the two ele-

ments (B,A) from Stack 2

A B,A The element at the top of Stack 2 is

identical to A, so remove the two ele-

ments (B,A) from Stack 2

A empty

Now Stack 2 is empty and Phase 2 ends. Since Stack 1 is not empty, the

algorithm correctly outputs A as the majority element. We also see that the

algorithm has made only four comparisons in Phase 2. In the ﬁrst of the

four comparisons the result of the comparison was already clear in advance

(as explained by the remark in brackets), so the number of comparisons that

actually need to be performed in Phase 2 is only three.

Let us brieﬂy sketch the analysis that shows that the reﬁned majority

algorithm is correct. Essentially, the role of the stack in the ﬁrst majority

246 Thomas Erlebach

algorithm is now performed by Stack 1 together with the top element of

Stack 2. Furthermore, the elements in Stack 1 are identical at any time (and

are also identical to the top element of Stack 2). Besides, it can never happen

that two identical elements are placed in Stack 2 directly next to each other

(i.e., one directly on top of the other). This implies that the element Y that is

at the top of Stack 2 at the end of Phase 1 is the only possible candidate for a

majority element. Each iteration of Phase 2 then removes two elements, one of

which is identical to Y and one of which is diﬀerent from Y. It follows that Y is

the majority element if and only if Stack 1 is not empty at the end of Phase 2

(and thus still contains at least one Y). This establishes the correctness of the

reﬁned majority algorithm. Regarding the number of comparisons, we ﬁnd

that the algorithm makes at most N −1 comparisons in Phase 1 and at most

N/2−1 comparisons in Phase 2 (the latter holds because in each iteration

of Phase 2 two elements are removed, but only one comparison is made; this

can also be seen in the example above). This means that the algorithm needs

at most 3N/2−2 comparisons to identify the majority element (or to detect

that there is none).

Can we do even better than that? This time the answer is negative. One

can prove that every algorithm requires at least 3N/2−2 comparisons on

some input with N elements. Consequently, it is impossible to beat the reﬁned

majority algorithm with respect to the number of comparisons that it needs

in the worst case.

Applications and Extensions

The majority problem occurs not only in the context of elections, but also

in various other applications. For example, consider safety-critical computa-

tions where a correct result is extremely important. Such computations can

be carried out by N diﬀerent processors in parallel, and the majority ele-

ment of the N solutions computed by the diﬀerent processors is then taken

as the result. This method ensures that as long as less than half of the pro-

cessors are faulty and produce a wrong solution, one still obtains the correct

result.

Among N given elements, an element is the majority element if it occurs

more than N/2 times. As a generalization of this concept, one can consider

frequent elements, i.e., elements that occur more than N/K times, where K is

a ﬁxed number. For example, for K = 10 these are elements that occur with

a frequency larger than 10%. Identifying frequent elements is a very relevant

problem in the context of monitoring Internet traﬃc, because one wants to

know which applications or users produce the largest amount of traﬃc. As

data packets need to be processed extremely quickly, one needs an algorithm

that can handle each new packet in the shortest possible time. The majority

algorithm can be generalized to solve such problems.

24 Majority – Who Gets Elected Class Rep? 247

What Can We Learn from the Solutions to the Majority

Problem?

• The most straightforward solution to a problem is not always the fastest

one.

• Often there are clever algorithms that can solve the same task with much

less eﬀort.

• It is not always easy to see whether an algorithm produces the correct

result for every possible input.

• Sometimes one can prove that for a problem it is impossible to ﬁnd an

algorithm that is better than the one we already have.